Aritmética Hexadecimal
Sistema numérico hexadecimal
A seguir estão as características de um sistema numérico hexadecimal.
Usa 10 dígitos e 6 letras, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
As letras representam números começando em 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Também chamado de sistema numérico de base 16.
Cada posição em um número hexadecimal representa uma potência 0 da base (16). Exemplo - 16 0
A última posição em um número hexadecimal representa uma potência x da base (16). Exemplo - 16 x onde x representa a última posição - 1.
Exemplo
Número hexadecimal - 19FDE 16
Calculando o Equivalente Decimal -
| Degrau | Número Hexadecimal | Número decimal |
|---|---|---|
| Passo 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Passo 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| etapa 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Passo 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 é normalmente escrito como 19FDE.
Adição Hexadecimal
A tabela de adição hexadecimal a seguir o ajudará muito a lidar com a adição hexadecimal.
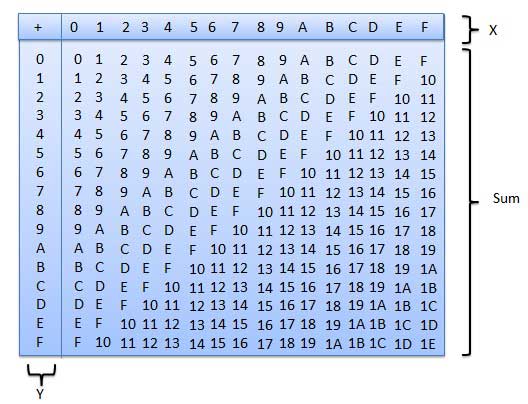
Para usar esta tabela, basta seguir as instruções usadas neste exemplo - Adicionar A 16 e 5 16 . Localize A na coluna X e, a seguir, localize 5 na coluna Y. O ponto na área de 'soma' onde essas duas colunas se cruzam é a soma de dois números.
A16 + 516 = F16.Exemplo - Adição
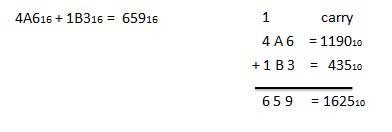
Subtração Hexadecimal
A subtração de números hexadecimais segue as mesmas regras que a subtração de números em qualquer outro sistema numérico. A única variação está no número emprestado. No sistema decimal, você toma emprestado um grupo de 10 10 . No sistema binário, você toma emprestado um grupo de 2 10 . No sistema hexadecimal, você toma emprestado um grupo de 16 10 .
Exemplo - Subtração
