Modelando Multiplicação de Frações Adequadas
Vamos usar um modelo de área para multiplicar as frações. O modelo de área nos dá uma boa imagem do que acontece quando multiplicamos duas frações. Vemos o problema em duas dimensões. Representamos a altura usando uma fração e a largura usando outra fração. É importante ver esse tipo de conexão na matemática.
Multiplique as frações usando um modelo de área $ \ frac {1} {3} $ × $ \ frac {1} {3} $
Solução
Step 1:
Neste problema, queremos encontrar $ \ frac {1} {3} $ de $ \ frac {1} {3} $
Step 2:
Primeiro, dividimos a altura de um retângulo em 3 partes iguais.

Step 3:
Sombrimos uma parte para representar $ \ frac {1} {3} $

Step 4:
Em seguida, dividimos a largura em 3 partes iguais e sombreamos 1 parte para torná-la $ \ frac {1} {3} $
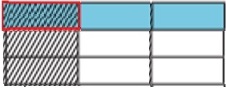
Step 5:
Agora podemos descobrir o produto. A parte onde o sombreamento se sobrepõe representa o numerador. O número total de peças representa o denominador. Existem 9 partes no total e 1 das partes se sobrepõe.
Step 6:
Portanto, o produto é $ \ frac {1} {9} $ .
$ \ frac {1} {3} $ × $ \ frac {1} {3} $ = $ \ frac {1} {9} $
Multiplique as frações usando um modelo de área $ \ frac {2} {3} $ × $ \ frac {1} {3} $
Solução
Step 1:
Neste problema, queremos encontrar $ \ frac {2} {3} $ de $ \ frac {1} {3} $
Step 2:
Primeiro, dividimos a altura de um retângulo em 3 partes iguais.

Step 3:
Sombrimos uma parte para representar $ \ frac {1} {3} $

Step 4:
Em seguida, dividimos a largura em 3 partes iguais e sombreamos 2 partes para torná-la $ \ frac {2} {3} $
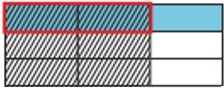
Step 5:
Agora podemos descobrir o produto. A parte onde o sombreamento se sobrepõe representa o numerador. O número total de peças representa o denominador. Existem 9 partes no total e 2 das partes se sobrepõem.
Step 6:
Portanto, o produto é $ \ frac {2} {9} $ .
$ \ frac {2} {3} $ × $ \ frac {1} {3} $ = $ \ frac {2} {9} $
Multiplique as frações usando um modelo de área $ \ frac {1} {2} $ × $ \ frac {1} {3} $
Solução
Step 1:
Neste problema, queremos encontrar $ \ frac {1} {2} $ de $ \ frac {1} {3} $
Step 2:
Primeiro, dividimos a altura de um retângulo em 3 partes iguais.

Step 3:
Sombrimos uma parte para representar $ \ frac {1} {3} $

Step 4:
Em seguida, dividimos a largura em 2 partes iguais e sombreamos 1 parte para torná-la $ \ frac {1} {2} $
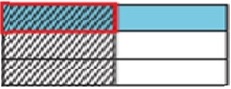
Step 5:
Agora podemos descobrir o produto. A parte onde o sombreamento se sobrepõe representa o numerador. O número total de peças representa o denominador. Existem 6 partes no total e 1 das partes se sobrepõe.
Step 6:
Portanto, o produto é $ \ frac {1} {6} $ .
$ \ frac {1} {2} $ × $ \ frac {1} {3} $ = $ \ frac {1} {6} $