Аналоговая связь - угловая модуляция
Другой тип модуляции при непрерывной модуляции - это Angle Modulation. Угловая модуляция - это процесс, при котором частота или фаза несущего сигнала изменяется в соответствии с сигналом сообщения.
Стандартное уравнение волны с угловой модуляцией:
$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$
Куда,
$ A_c $ - это амплитуда модулированной волны, которая совпадает с амплитудой несущего сигнала.
$ \ theta _i \ left (t \ right) $ - угол модулированной волны
Угловая модуляция подразделяется на частотную модуляцию и фазовую модуляцию.
Frequency Modulation представляет собой процесс изменения частоты несущего сигнала линейно с сигналом сообщения.
Phase Modulation - это процесс линейного изменения фазы несущего сигнала в зависимости от сигнала сообщения.
Теперь давайте обсудим это подробнее.
Модуляция частоты
При амплитудной модуляции изменяется амплитуда несущего сигнала. Тогда как вFrequency Modulation (FM), частота несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.
Следовательно, при частотной модуляции амплитуда и фаза несущего сигнала остаются постоянными. Это можно лучше понять, наблюдая за следующими рисунками.
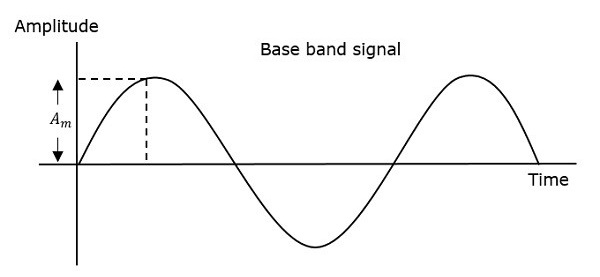


Частота модулированной волны увеличивается, когда увеличивается амплитуда модулирующего сигнала или сигнала сообщения. Точно так же частота модулированной волны уменьшается, когда уменьшается амплитуда модулирующего сигнала. Обратите внимание, что частота модулированной волны остается постоянной и равна частоте несущего сигнала, когда амплитуда модулирующего сигнала равна нулю.
Математическое представление
Уравнение для мгновенной частоты $ f_i $ при модуляции FM имеет вид
$$ f_i = f_c + k_fm \ left (t \ right) $$
Куда,
$ f_c $ - несущая частота
$ k_t $ - частотная чувствительность
$ m \ left (t \ right) $ - сигнал сообщения
Нам известна связь между угловой частотой $ \ omega_i $ и углом $ \ theta _i \ left (t \ right) $ как
$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$
$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $
Подставьте значение $ f_i $ в приведенное выше уравнение.
$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $$
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $
Подставьте значение $ \ theta _i \ left (t \ right) $ в стандартное уравнение волны с угловой модуляцией.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
Это equation of FM wave.
Если модулирующий сигнал равен $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, то уравнение FM-волны будет
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
Куда,
$ \ beta $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $
Разница между FM-модулированной частотой (мгновенной частотой) и нормальной несущей частотой называется Frequency Deviation. Он обозначается $ \ Delta f $, что равно произведению $ k_f $ и $ A_m $.
FM можно разделить на Narrowband FM а также Wideband FM на основе значений индекса модуляции $ \ beta $.
Узкополосный FM
Ниже приведены особенности Narrowband FM.
Эта частотная модуляция имеет небольшую полосу пропускания по сравнению с широкополосной ЧМ.
Индекс модуляции $ \ beta $ небольшой, т.е. меньше 1.
Его спектр состоит из несущей, верхней и нижней боковых полос.
Это используется в мобильной связи, такой как полицейская беспроводная связь, машины скорой помощи, такси и т. Д.
Широкополосный FM
Ниже приведены особенности широкополосного FM.
Эта частотная модуляция имеет бесконечную полосу пропускания.
Индекс модуляции $ \ beta $ велик, т.е. больше 1.
Его спектр состоит из несущей и бесконечного числа боковых полос, расположенных вокруг нее.
Это используется в развлекательных, вещательных приложениях, таких как FM-радио, телевидение и т. Д.
Фазовая модуляция
При частотной модуляции частота несущей меняется. Тогда как вPhase Modulation (PM), фаза несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.
Таким образом, при фазовой модуляции амплитуда и частота несущего сигнала остаются постоянными. Это можно лучше понять, наблюдая за следующими рисунками.
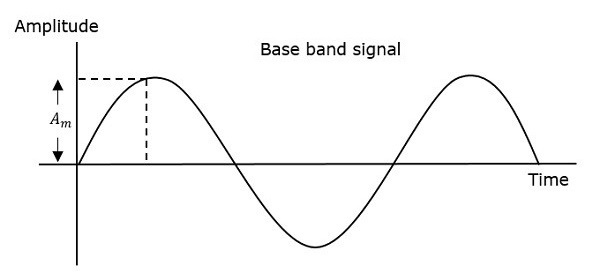

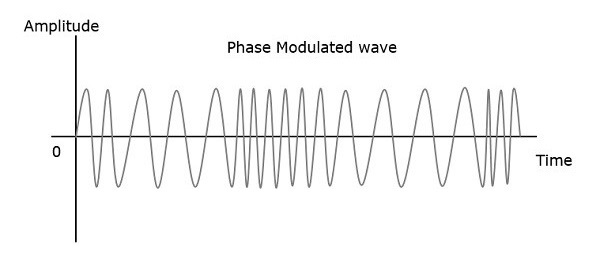
Фаза модулированной волны имеет бесконечное количество точек, где может иметь место фазовый сдвиг в волне. Мгновенная амплитуда модулирующего сигнала изменяет фазу несущего сигнала. Когда амплитуда положительная, фаза изменяется в одном направлении, а если амплитуда отрицательная, фаза изменяется в противоположном направлении.
Математическое представление
Уравнение мгновенной фазы $ \ phi_i $ при фазовой модуляции имеет вид
$$ \ phi _i = k_p m \ left (t \ right) $$
Куда,
$ k_p $ - фазовая чувствительность
$ m \ left (t \ right) $ - сигнал сообщения
Стандартное уравнение волны с угловой модуляцией:
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$
Подставьте значение $ \ phi_i $ в приведенное выше уравнение.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right) $$
Это equation of PM wave.
Если модулирующий сигнал, $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, то уравнение PM волны будет
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right) $$
Куда,
$ \ beta $ = modulation index = $ \ Delta \ phi = k_pA_m $
$ \ Delta \ phi $ - отклонение фазы
Фазовая модуляция используется в системах мобильной связи, а частотная модуляция используется в основном для FM-вещания.