Аналоговая связь - отбор проб
До сих пор мы обсуждали непрерывную модуляцию. Мы обсудим импульсную модуляцию в следующей главе. Эти методы импульсной модуляции работают с дискретными сигналами. Итак, теперь давайте посмотрим, как преобразовать непрерывный сигнал времени в дискретный.
Процесс преобразования сигналов непрерывного времени в эквивалентные сигналы дискретного времени можно обозначить как Sampling. В процессе выборки непрерывно производится выборка данных в определенный момент.
На следующем рисунке показан непрерывный сигнал. x(t) и соответствующий дискретизированный сигнал xs(t). когдаx(t) умножается на периодическую последовательность импульсов, дискретизированный сигнал xs(t) получается.

А sampling signal представляет собой периодическую серию импульсов единичной амплитуды, дискретизируемую через равные промежутки времени $ T_s $, которая называется sampling time. Эти данные передаются в моменты времени $ T_s $, а сигнал несущей передается в оставшееся время.
Частота выборки
Для дискретизации сигналов необходимо устранить разрыв между отсчетами. Этот промежуток можно назвать периодом выборки $ T_s $. Взаимность периода выборки известна какsampling frequency или sampling rate $f_s$.
Математически мы можем записать это как
$$ f_s = \ frac {1} {T_s} $$
Куда,
$ f_s $ - частота дискретизации или частота дискретизации
$ T_s $ - период выборки
Теорема выборки
Частота дискретизации должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Вsampling theorem утверждает, что «сигнал может быть точно воспроизведен, если он дискретизируется со скоростью $ f_s $, которая больше или равна удвоенной максимальной частоте данного сигнала. W. »
Математически мы можем записать это как
$$ f_s \ geq 2W $$
Куда,
$ f_s $ - частота дискретизации
$ W $ - самая высокая частота данного сигнала
Если частота дискретизации равна удвоенной максимальной частоте данного сигнала W, то она называется Nyquist rate.
Теорема выборки, которую также называют Nyquist theorem, предоставляет теорию достаточной частоты дискретизации с точки зрения полосы пропускания для класса функций с ограниченной полосой пропускания.
Для сигнала непрерывного времени x(t), которая ограничена полосой частот в частотной области, представлена, как показано на следующем рисунке.

Если частота дискретизации сигнала превышает частоту Найквиста, то исходный сигнал может быть восстановлен. На следующем рисунке поясняется сигнал, если частота дискретизации выше, чем у2w в частотной области.
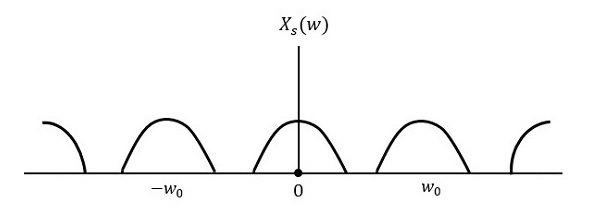
Если тот же сигнал дискретизируется с частотой менее 2w, то дискретизированный сигнал будет выглядеть как на следующем рисунке.

Из приведенного выше рисунка видно, что информация перекрывается, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называетсяAliasing.
Наложение наложения можно назвать «явлением высокочастотной составляющей в спектре сигнала, которая приобретает идентичность низкочастотной составляющей в спектре его дискретизированной версии».
Следовательно, частота дискретизации сигнала выбирается равной частоте Найквиста. Если частота дискретизации равна удвоенной максимальной частоте данного сигналаW, то дискретизированный сигнал будет выглядеть как на следующем рисунке.

В этом случае сигнал можно восстановить без потерь. Следовательно, это хорошая частота дискретизации.