Аналоговая связь - Краткое руководство
Слово общение происходит от латинского слова commūnicāre, что означает «делиться». Общение - это основной шаг для обмена информацией.
Например, ребенок в колыбели общается криком, когда ей нужна мама. Корова громко мычит, когда ей угрожает опасность. Человек общается с помощью языка. Общение - это мост, которым можно поделиться.
Communication можно определить как процесс обмена информацией с помощью таких средств, как слова, действия, знаки и т. д., между двумя или более людьми.
Части коммуникационной системы
Любая система, обеспечивающая связь, состоит из трех основных и основных частей, как показано на следующем рисунке.

Senderэто человек, который отправляет сообщение. Это может быть передающая станция, откуда передается сигнал.
Channel это среда, через которую проходят сообщения сообщения, чтобы достичь пункта назначения.
Receiverэто человек, который получает сообщение. Это может быть приемная станция, на которой принимается передаваемый сигнал.
Типы сигналов
Передачу информации некоторыми средствами, такими как жесты, звуки, действия и т. Д., Можно назвать signaling. Следовательно, сигнал может быть источником энергии, который передает некоторую информацию. Этот сигнал помогает установить связь между отправителем и получателем.
Электрический импульс или электромагнитная волна, которая распространяется на расстояние, чтобы передать сообщение, может быть названа signal в системах связи.
В зависимости от характеристик сигналы в основном делятся на два типа: аналоговые и цифровые. Аналоговые и цифровые сигналы дополнительно классифицируются, как показано на следующем рисунке.

Аналоговый сигнал
Непрерывный изменяющийся во времени сигнал, который представляет изменяющуюся во времени величину, можно назвать Analog Signal. Этот сигнал продолжает изменяться во времени в соответствии с мгновенными значениями представляющей его величины.
пример
Рассмотрим кран, наполняющий бак емкостью 100 литров за час (с 6 утра до 7 утра). Порция наполнения бака варьируется разным временем. Это означает, что через 15 минут (6:15 утра) четверть резервуара будет заполнена, тогда как в 6:45 утра будет заполнено 3/4 резервуара.
Если мы попытаемся изобразить изменяющиеся порции воды в резервуаре в соответствии с изменяющимся временем, это будет выглядеть, как на следующем рисунке.

Поскольку результат, показанный на этом изображении, изменяется (увеличивается) со временем, это time varying quantityможно понимать как аналоговую величину. Сигнал, который представляет это состояние наклонной линией на рисунке, представляет собойAnalog Signal. Связь на основе аналоговых сигналов и аналоговых значений называетсяAnalog Communication.
Цифровой сигнал
Сигнал, который является дискретным или непостоянным по форме, можно назвать Digital signal. Этот сигнал имеет отдельные значения, обозначенные отдельно, которые не основаны на предыдущих значениях, как если бы они были получены в этот конкретный момент времени.
пример
Рассмотрим класс из 20 учеников. Если построить график их посещаемости за неделю, это будет выглядеть как на следующем рисунке.

На этом рисунке значения указаны отдельно. Например, посещаемость класса в среду - 20, а в субботу - 15. Эти значения можно рассматривать индивидуально и отдельно или по отдельности, поэтому они называютсяdiscrete values.
Двоичные цифры, в которых есть только единицы и нули, в основном называются digital values. Следовательно, сигналы, которые представляют единицы и нули, также называютсяdigital signals. Связь на основе цифровых сигналов и цифровых значений называетсяDigital Communication.
Периодический сигнал
Любой аналоговый или цифровой сигнал, повторяющийся в течение определенного периода времени, называется Periodic Signal. Этот сигнал повторяется неоднократно, и его легко предположить или вычислить.
пример
Если мы рассмотрим оборудование в отрасли, процесс, который происходит один за другим, является непрерывной процедурой. Например, заготовка и сортировка сырья, обработка материала партиями, упаковка продуктов одна за другой и т. Д. Повторяют определенную процедуру многократно.
Такой процесс, будь то аналоговый или цифровой, можно графически представить следующим образом.

Апериодический сигнал
Любой аналоговый или цифровой сигнал, который не повторяет свой образец в течение определенного периода времени, называется Aperiodic Signal. Этот сигнал продолжает свой паттерн, но паттерн не повторяется. Это также не так-то просто предположить или рассчитать.
пример
Ежедневный распорядок человека, если его рассматривать, состоит из различных видов работы, которые требуют разных временных интервалов для выполнения различных задач. Временной интервал или работа не повторяется постоянно. Например, человек не будет чистить зубы непрерывно с утра до вечера, причем в один и тот же период времени.
Такой процесс, будь то аналоговый или цифровой, можно графически представить следующим образом.


В общем, сигналы, которые используются в системах связи, являются аналоговыми по своей природе, которые передаются в аналоговом виде или преобразуются в цифровые, а затем передаются, в зависимости от требований.
Чтобы сигнал передавался на расстояние без воздействия каких-либо внешних помех или добавления шума и не затухал, он должен пройти процесс, называемый Modulation. Он улучшает мощность сигнала, не нарушая параметров исходного сигнала.
Что такое модуляция?
Сообщение, несущее сигнал, должно передаваться на расстояние, и для установления надежной связи ему необходимо использовать высокочастотный сигнал, который не должен влиять на исходные характеристики сигнала сообщения.
Характеристики сигнала сообщения, при изменении, содержащееся в нем сообщение также изменяется. Следовательно, необходимо позаботиться о сигнале сообщения. Высокочастотный сигнал может распространяться на большее расстояние, не подвергаясь воздействию внешних помех. Воспользуемся помощью такого высокочастотного сигнала, который называетсяcarrier signalдля передачи нашего сигнала сообщения. Такой процесс называется просто модуляцией.
Модуляция - это процесс изменения параметров несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Потребность в модуляции
Сигналы основной полосы частот несовместимы для прямой передачи. Чтобы такой сигнал мог перемещаться на большие расстояния, его сила должна быть увеличена путем модуляции высокочастотной несущей волной, которая не влияет на параметры модулирующего сигнала.
Преимущества модуляции
Антенна, используемая для передачи, должна была быть очень большой, если не вводилась модуляция. Диапазон связи становится ограниченным, поскольку волна не может преодолевать расстояние, не искажаясь.
Ниже приведены некоторые преимущества реализации модуляции в системах связи.
- Уменьшение размера антенны
- Нет смешивания сигналов
- Увеличенная дальность связи
- Мультиплексирование сигналов
- Возможность регулировки полосы пропускания
- Улучшено качество приема
Сигналы в процессе модуляции
Ниже приведены три типа сигналов в процессе модуляции.
Сообщение или модулирующий сигнал
Сигнал, содержащий сообщение, которое нужно передать, называется message signal. Это сигнал основной полосы частот, который должен пройти процесс модуляции для передачи. Следовательно, его также называютmodulating signal.
Несущий сигнал
Высокочастотный сигнал, который имеет определенную амплитуду, частоту и фазу, но не содержит информации, называется carrier signal. Это пустой сигнал, который используется для передачи сигнала приемнику после модуляции.
Модулированный сигнал
Результирующий сигнал после процесса модуляции называется modulated signal. Этот сигнал представляет собой комбинацию модулирующего сигнала и сигнала несущей.
Типы модуляции
Есть много видов модуляции. В зависимости от используемых методов модуляции они классифицируются, как показано на следующем рисунке.

Типы модуляции в целом подразделяются на непрерывную модуляцию и импульсную модуляцию.
Непрерывная модуляция
При непрерывной модуляции в качестве несущей используется высокочастотная синусоида. Далее это делится на амплитудную и угловую модуляцию.
Если амплитуда высокочастотной несущей волны изменяется в соответствии с мгновенной амплитудой модулирующего сигнала, то такой метод называется Amplitude Modulation.
Если угол несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется Angle Modulation. Угловая модуляция подразделяется на частотную модуляцию и фазовую модуляцию.
Если частота несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется Frequency Modulation.
Если фаза высокочастотной несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется Phase Modulation.
Импульсная модуляция
В импульсной модуляции в качестве несущей используется периодическая последовательность прямоугольных импульсов. Далее это делится на аналоговую и цифровую модуляцию.
В методе аналоговой модуляции, если амплитуда, продолжительность или положение импульса изменяется в соответствии с мгновенными значениями модулирующего сигнала основной полосы частот, то такой метод называется амплитудно-импульсной модуляцией (PAM) или длительностью / широтно-импульсной модуляцией (PDM). / PWM) или импульсной позиционной модуляцией (PPM).
В цифровой модуляции используется метод модуляции - импульсно-кодовая модуляция (ИКМ), при которой аналоговый сигнал преобразуется в цифровую форму единиц и нулей. Поскольку в результате получается последовательность кодированных импульсов, она называется ИКМ. Это далее развивается как дельта-модуляция (DM). Эти методы цифровой модуляции обсуждаются в нашем руководстве по цифровой связи.
Непрерывная волна идет непрерывно без каких-либо интервалов, и это сигнал сообщения основной полосы частот, который содержит информацию. Эта волна должна быть модулирована.
Согласно стандартному определению, «амплитуда несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала». Это означает, что амплитуда несущего сигнала, не содержащего информации, изменяется в каждый момент в соответствии с амплитудой сигнала, содержащего информацию. Это хорошо объясняется следующими цифрами.



На первом рисунке показана модулирующая волна, являющаяся сигналом сообщения. Следующая - это несущая волна, которая является высокочастотным сигналом и не содержит информации. А последняя - результирующая модулированная волна.
Можно заметить, что положительный и отрицательный пики несущей волны связаны между собой воображаемой линией. Эта линия помогает воссоздать точную форму модулирующего сигнала. Эта воображаемая линия на несущей волне называетсяEnvelope. Это то же самое, что и у сигнала сообщения.
Математические выражения
Ниже приведены математические выражения для этих волн.
Представление волн во временной области
Пусть модулирующий сигнал равен,
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
и несущий сигнал будет,
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Где,
$ A_m $ и $ A_c $ - амплитуда модулирующего сигнала и сигнала несущей соответственно.
$ f_m $ и $ f_c $ - частота модулирующего сигнала и сигнала несущей соответственно.
Тогда уравнение амплитудно-модулированной волны будет
$ s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ (Уравнение 1)
Индекс модуляции
Несущая волна после модуляции, если рассчитан модулированный уровень, такая попытка называется Modulation Index или же Modulation Depth. В нем указывается уровень модуляции несущей волны.
Переставьте уравнение 1, как показано ниже.
$ s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ right) \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ ( Уравнение 2)
Где $ \ mu $ - это индекс модуляции, равный отношению $ A_m $ и $ A_c $. Математически мы можем записать это как
$ \ mu = \ frac {A_m} {A_c} $ (Уравнение 3)
Следовательно, мы можем вычислить значение индекса модуляции, используя приведенную выше формулу, когда известны амплитуды сигналов сообщения и несущей.
Теперь давайте выведем еще одну формулу для индекса модуляции, рассматривая уравнение 1. Мы можем использовать эту формулу для вычисления значения индекса модуляции, когда известны максимальная и минимальная амплитуды модулированной волны.
Пусть $ A_ \ max $ и $ A_ \ min $ - максимальная и минимальная амплитуды модулированной волны.
Мы получим максимальную амплитуду модулированной волны, когда $ \ cos \ left (2 \ pi f_mt \ right) $ равно 1.
$ \ Rightarrow A_ \ max = A_c + A_m $ (Уравнение 4)
Мы получим минимальную амплитуду модулированной волны, когда $ \ cos \ left (2 \ pi f_mt \ right) $ равно -1.
$ \ Rightarrow A_ \ min = A_c - A_m $ (Уравнение 5)
Складываем уравнение 4 и уравнение 5.
$$ A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c $$
$ \ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2} $ (Уравнение 6)
Вычтите уравнение 5 из уравнения 4.
$$ A_ \ max - A_ \ min = A_c + A_m - \ left (A_c -A_m \ right) = 2A_m $$
$ \ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2} $ (Уравнение 7)
Соотношение уравнения 7 и уравнения 6 будет следующим.
$$ \ frac {A_m} {A_c} = \ frac {\ left (A_ {max} - A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ right) / 2 } $$
$ \ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min} $ (уравнение 8)
Следовательно, уравнение 3 и уравнение 8 являются двумя формулами для индекса модуляции. Индекс модуляции или глубина модуляции часто обозначается в процентах, называемых процентами модуляции. Мы получимpercentage of modulation, просто умножив значение индекса модуляции на 100.
Для идеальной модуляции значение индекса модуляции должно быть 1, что означает, что процент модуляции должен составлять 100%.
Например, если это значение меньше 1, т. Е. Индекс модуляции равен 0,5, то модулированный выход будет выглядеть, как на следующем рисунке. Это называетсяUnder-modulation. Такая волна называетсяunder-modulated wave.

Если значение индекса модуляции больше 1, т. Е. 1,5 или около того, тогда волна будет over-modulated wave. Это выглядело бы как на следующем рисунке.

По мере увеличения значения индекса модуляции несущая испытывает переворот фазы на 180 o , что вызывает дополнительные боковые полосы и, следовательно, искажает волну. Такая перемодулированная волна вызывает помехи, которые невозможно устранить.
Полоса пропускания AM волны
Bandwidth(BW) - разница между самой высокой и самой низкой частотами сигнала. Математически мы можем записать это как
$$ BW = f_ {max} - f_ {min} $$
Рассмотрим следующее уравнение амплитудно-модулированной волны.
$$ s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
Следовательно, амплитудно-модулированная волна имеет три частоты. Это несущая частота $ f_c $, частота верхней боковой полосы $ f_c + f_m $ и частота нижней боковой полосы $ f_c-f_m $.
Вот,
$ f_ {max} = f_c + f_m $ и $ f_ {min} = f_c-f_m $
Замените значения $ f_ {max} $ и $ f_ {min} $ в формуле пропускной способности.
$$ BW = f_c + f_m- \ left (f_c-f_m \ right) $$
$$ \ Rightarrow BW = 2f_m $$
Таким образом, можно сказать, что ширина полосы, необходимая для амплитудно-модулированной волны, в два раза превышает частоту модулирующего сигнала.
Расчет мощности AM волны
Рассмотрим следующее уравнение амплитудно-модулированной волны.
$ \ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
Мощность AM волны равна сумме мощностей частотных составляющих несущей, верхней боковой полосы и нижней боковой полосы.
$$ P_t = P_c + P_ {USB} + P_ {LSB} $$
Мы знаем, что стандартная формула для мощности сигнала cos
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2} $$
Где,
$ v_ {rms} $ - среднеквадратичное значение сигнала cos.
$ v_m $ - пиковое значение сигнала cos.
Во-первых, давайте по очереди найдем мощности несущей, верхней и нижней боковых полос.
Несущая мощность
$$ P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R} $$
Мощность верхней боковой полосы
$$ P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
Точно так же мы получим мощность нижней боковой полосы, такую же, как мощность верхней боковой полосы.
$$ P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
Теперь давайте сложим эти три мощности, чтобы получить мощность AM волны.
$$ P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
$$ \ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ right) $$
$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$
Мы можем использовать приведенную выше формулу для расчета мощности AM волны, когда известны мощность несущей и индекс модуляции.
Если индекс модуляции $ \ mu = 1 $, то мощность AM-волны в 1,5 раза превышает мощность несущей. Таким образом, мощность, необходимая для передачи AM-волны, в 1,5 раза превышает мощность несущей для идеальной модуляции.
В предыдущей главе мы обсудили параметры, используемые в амплитудной модуляции. У каждого параметра своя формула. Используя эти формулы, мы можем найти соответствующие значения параметров. В этой главе давайте решим несколько задач, основанных на концепции амплитудной модуляции.
Проблема 1
Модулирующий сигнал $ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $ модулируется по амплитуде несущим сигналом $ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5 t \ right) $. Найдите индекс модуляции, мощность несущей и мощность, необходимую для передачи AM-волны.
Решение
Учитывая, что уравнение модулирующего сигнала как
$$ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $$
Мы знаем стандартное уравнение модулирующего сигнала как
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
Сравнивая два приведенных выше уравнения, мы получим
Амплитуда модулирующего сигнала как $ A_m = 10 вольт $
и частота модулирующего сигнала как $$ f_m = 10 ^ 3 Гц = 1 кГц $$
Учитывая, что уравнение несущего сигнала имеет вид
$$ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5t \ right) $$
Стандартное уравнение несущего сигнала:
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Сравнивая эти два уравнения, мы получим
Амплитуда несущего сигнала как $ A_c = 50volts $
и Частота несущего сигнала как $ f_c = 10 ^ 5 Гц = 100 кГц $
Мы знаем формулу для индекса модуляции как
$$ \ mu = \ frac {A_m} {A_c} $$
Подставьте значения $ A_m $ и $ A_c $ в формулу выше.
$$ \ mu = \ frac {10} {50} = 0,2 $$
Следовательно, значение modulation index is 0.2 и процент модуляции составляет 20%.
Формула для несущей мощности $ P_c = $:
$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$
Предположим, что $ R = 1 \ Omega $, и подставим значение $ A_c $ в приведенную выше формулу.
$$ P_c = \ frac {\ left (50 \ right) ^ 2} {2 \ left (1 \ right)} = 1250 Вт $$
Следовательно Carrier power, $ P_c $ - это 1250 watts.
Мы знаем формулу для power требующийся для transmitting AM волна
$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$
Подставьте значения $ P_c $ и $ \ mu $ в приведенную выше формулу.
$$ P_t = 1250 \ left (1+ \ frac {\ left (0,2 \ right) ^ 2} {2} \ right) = 1275 Вт $$
Следовательно power required for transmitting AM волна 1275 watts.
Проблема 2
Уравнение амплитудной волны задается следующим образом: $ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $. Найдите мощность несущей, общую мощность боковой полосы и ширину полосы АМ волны.
Решение
Учитывая, что уравнение амплитудно-модулированной волны имеет вид
$$ s \ left (t \ right) = 20 \ left [1 + 0,8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $$
Перепишите приведенное выше уравнение как
$$ s \ left (t \ right) = 20 \ left [1 + 0,8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (2 \ pi \ times 2 \ times 10 ^ 5t \ вправо) $$
Мы знаем, что уравнение амплитудно-модулированной волны имеет вид
$$ s \ left (t \ right) = A_c \ left [1+ \ mu \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Сравнивая два приведенных выше уравнения, мы получим
Амплитуда несущего сигнала как $ A_c = 20 вольт $
Индекс модуляции как $ \ mu = 0,8 $
Частота модулирующего сигнала как $ f_m = 10 ^ 3Hz = 1 KHz $
Частота несущего сигнала как $ f_c = 2 \ times 10 ^ 5Hz = 200KHz $
Формула для несущей мощности $ P_c $:
$$ P_c = \ frac {{A_ {e}} ^ {2}} {2R} $$
Предположим, что $ R = 1 \ Omega $, и подставим значение $ A_c $ в приведенную выше формулу.
$$ P_c = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200 Вт $$
Следовательно Carrier power, $ P_c $ - это 200watts.
Мы знаем, что формула для полной мощности боковой полосы:
$$ P_ {SB} = \ frac {P_c \ mu ^ 2} {2} $$
Подставьте значения $ P_c $ и $ \ mu $ в приведенную выше формулу.
$$ P_ {SB} = \ frac {200 \ times \ left (0.8 \ right) ^ 2} {2} = 64W $$
Следовательно total side band power является 64 watts.
Мы знаем, что формула для ширины полосы АМ-волны:
$$ BW = 2f_m $$
Подставьте значение $ f_m $ в приведенную выше формулу.
$$ BW = 2 \ left (1K \ right) = 2 кГц $$
Следовательно bandwidth волны AM составляет 2 KHz.
В этой главе давайте обсудим модуляторы, которые генерируют амплитудно-модулированную волну. Следующие два модулятора генерируют AM-волну.
- Модулятор квадратичного закона
- Модулятор переключения
Модулятор квадратного закона
Ниже представлена блок-схема модулятора квадратичного закона.

Обозначим модулирующий и несущий сигналы как $ m \ left (t \ right) $ и $ A \ cos \ left (2 \ pi f_ct \ right) $ соответственно. Эти два сигнала используются как входы в сумматор (сумматор). Этот летний блок формирует выходной сигнал, который является сложением модулирующего и несущего сигнала. Математически мы можем записать это как
$$ V_1t = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) $$
Этот сигнал $ V_1t $ подается на вход нелинейного устройства, такого как диод. Характеристики диода тесно связаны с квадратичным законом.
$ V_2t = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right) $ (Уравнение 1)
Где $ k_1 $ и $ k_2 $ - константы.
Подставьте $ V_1 \ left (t \ right) $ в уравнение 1.
$$ V_2 \ left (t \ right) = k_1 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] + k_2 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] ^ 2 $$
$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ right) + k_2 m ^ 2 \ left (t \ right) + $
$ k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_2 m ^ 2 \ left (t \ right) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ справа) + $
$ k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $
Последний член приведенного выше уравнения представляет желаемую волну AM, а первые три члена приведенного выше уравнения являются нежелательными. Итак, с помощью полосового фильтра мы можем пропустить только AM-волну и исключить первые три члена.
Следовательно, выходной сигнал модулятора квадратичного закона равен
$$ s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Стандартное уравнение AM волны:
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Где, $ K_a $ - амплитудная чувствительность
Сравнивая выходной сигнал модулятора квадратичного закона со стандартным уравнением AM волны, мы получим масштабный коэффициент как $ k_1 $ и амплитудную чувствительность $ k_a $ как $ \ frac {2k_2} {k1} $.
Модулятор переключения
Ниже представлена блок-схема переключающего модулятора.

Переключающий модулятор аналогичен модулятору квадратичного закона. Единственное отличие состоит в том, что в модуляторах квадратичного закона диод работает в нелинейном режиме, тогда как в модуляторах переключения диод должен работать как идеальный переключатель.
Пусть модулирующий и несущий сигналы обозначены как $ m \ left (t \ right) $ и $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ соответственно. Эти два сигнала используются как входы в сумматор (сумматор). Блок Summer выдает выходной сигнал, который представляет собой сложение модулирующего и несущего сигналов. Математически мы можем записать это как
$$ V_1 \ left (t \ right) = m \ left (t \ right) + c \ left (t \ right) = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right ) $$
Этот сигнал $ V_1 \ left (t \ right) $ применяется как вход диода. Предположим, что величина модулирующего сигнала очень мала по сравнению с амплитудой несущего сигнала $ A_c $. Таким образом, включение и выключение диода контролируется несущим сигналом $ c \ left (t \ right) $. Это означает, что диод будет смещен в прямом направлении, когда $ c \ left (t \ right)> 0 $, и будет иметь обратное смещение, когда $ c \ left (t \ right) <0 $.
Следовательно, на выходе диода
$$ V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ right) <0 \ end {matrix} \ right. $$
Мы можем аппроксимировать это как
$ V_2 \ left (t \ right) = V_1 \ left (t \ right) x \ left (t \ right) $ (Уравнение 2)
Где $ x \ left (t \ right) $ - периодическая последовательность импульсов с периодом времени $ T = \ frac {1} {f_c} $

Эта периодическая последовательность импульсов представлена в виде ряда Фурье.
$$ x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ справа) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right) $$
$$ \ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + .... $$
Подставьте значения $ V_1 \ left (t \ right) $ и $ x \ left (t \ right) $ в уравнение 2.
$ V_2 \ left (t \ right) = \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] \ left [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ right] $
$ V_2 \ left (t \ right) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ right) - $
$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + ..... $
$ V_2 \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ справа) - $
$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + ..... $
1 - й член приведенного выше уравнения представляет собой желаемую АМ волну и остальные члены нежелательные термины. Таким образом, с помощью полосового фильтра мы можем пропустить только AM-волну и исключить остальные члены.
Следовательно, выходной сигнал модулятора переключения равен
$$ s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right ) \ cos \ left (2 \ pi f_ct \ right) $$
Мы знаем, что стандартное уравнение AM-волны:
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Где $ k_a $ - амплитудная чувствительность.
Сравнивая выходной сигнал переключающего модулятора со стандартным уравнением AM волны, мы получим масштабный коэффициент 0,5 и амплитудную чувствительность $ k_a $ как $ \ frac {4} {\ pi A_c} $.
Процесс извлечения исходного сигнала сообщения из модулированной волны известен как detection или же demodulation. Схема, которая демодулирует модулированную волну, известна какdemodulator. Следующие демодуляторы (детекторы) используются для демодуляции AM волны.
- Демодулятор квадратичного закона
- Детектор конвертов
Демодулятор квадратичного закона
Демодулятор квадратичного закона используется для демодуляции АМ волны низкого уровня. Ниже приведена блок-схемаsquare law demodulator.

Этот демодулятор содержит устройство квадратичного закона и фильтр нижних частот. AM-волна $ V_1 \ left (t \ right) $ используется в качестве входа в этот демодулятор.
Стандартная форма волны AM:
$$ V_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Мы знаем, что математическая связь между входом и выходом устройства квадратичного закона
$ V_2 \ left (t \ right) = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right) $ (Уравнение 1)
Где,
$ V_1 \ left (t \ right) $ - это вход устройства квадратичного закона, который является не чем иным, как волной AM
$ V_2 \ left (t \ right) $ - результат квадратичного устройства
$ k_1 $ и $ k_2 $ - константы
Подставьте $ V_1 \ left (t \ right) $ в уравнение 1.
$$ V_2 \ left (t \ right) = k_1 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) + k_2 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) ^ 2 $$
$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + $
$ k_2 {A_ {c}} ^ {2} \ left [1+ {K_ {a}} ^ {2} m ^ 2 \ left (t \ right) + 2k_am \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) $
$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {c}} ^ {2}} {2} + $
$ \ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ left (t \ right)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ left (t \ right)} {2} \ cos \ left (4 \ pi f_ct \ right) + $
$ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) + k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) \ cos \ left (4 \ pi f_ct \ справа) $
В приведенном выше уравнении член $ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) $ - это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот, а постоянную составляющую $ \ frac {k_2 {A_ {c}} ^ {2}} {2} $ можно устранить с помощью разделительного конденсатора.
Детектор конвертов
Детектор огибающей используется для обнаружения (демодуляции) АМ-волны высокого уровня. Ниже приведена блок-схема детектора огибающей.

Этот детектор огибающей состоит из диода и фильтра нижних частот. Здесь диод является основным детектирующим элементом. Следовательно, детектор огибающей также называютdiode detector. Фильтр нижних частот содержит параллельную комбинацию резистора и конденсатора.
AM-волна $ s \ left (t \ right) $ подается на вход этого детектора.
Мы знаем, что стандартная форма AM волны
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
В положительном полупериоде АМ волны диод проводит и конденсатор заряжается до пикового значения АМ волны. Когда значение волны AM меньше этого значения, диод будет смещен в обратном направлении. Таким образом, конденсатор разрядится через резисторRдо следующего положительного полупериода АМ волны. Когда величина волны AM больше, чем напряжение конденсатора, диод проводит ток, и процесс повторяется.
Мы должны выбирать значения компонентов таким образом, чтобы конденсатор заряжался очень быстро и очень медленно разряжался. В результате мы получим форму волны напряжения конденсатора, аналогичную форме огибающей волны AM, которая почти аналогична модулирующему сигналу.
В процессе амплитудной модуляции модулированная волна состоит из несущей и двух боковых полос. Модулированная волна имеет информацию только в боковых полосах.Sideband это не что иное, как полоса частот, содержащая мощность, которые представляют собой более низкие и высокие частоты несущей частоты.
Передачу сигнала, который содержит несущую вместе с двумя боковыми полосами, можно назвать Double Sideband Full Carrier система или просто DSBFC. Он построен, как показано на следующем рисунке.

Однако такая передача малоэффективна. Потому что две трети мощности тратится на носитель, который не несет никакой информации.
Если эта несущая подавляется и сохраненная мощность распределяется между двумя боковыми полосами, то такой процесс называется Double Sideband Suppressed Carrier система или просто DSBSC. Он построен, как показано на следующем рисунке.

Математические выражения
Давайте рассмотрим те же математические выражения для модулирующих сигналов и сигналов несущей, которые мы рассматривали в предыдущих главах.
т.е. модулирующий сигнал
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
Несущий сигнал
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Математически мы можем представить equation of DSBSC wave как продукт модулирующего и несущего сигналов.
$$ s \ left (t \ right) = m \ left (t \ right) c \ left (t \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$
Полоса пропускания DSBSC Wave
Мы знаем, что формула для ширины полосы пропускания (BW):
$$ BW = f_ {max} -f_ {min} $$
Рассмотрим уравнение модулированной волны DSBSC.
$$ s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos (2 \ pi f_ct) $$
$$ \ Rightarrow s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
Модулированная волна DSBSC имеет только две частоты. Итак, максимальная и минимальная частоты равны $ f_c + f_m $ и $ f_c-f_m $ соответственно.
т.е.
$ f_ {max} = f_c + f_m $ и $ f_ {min} = f_c-f_m $
Подставьте значения $ f_ {max} $ и $ f_ {min} $ в формулу пропускной способности.
$$ BW = f_c + f_m- \ left (f_c-f_m \ right) $$
$$ \ Rightarrow BW = 2f_m $$
Таким образом, ширина полосы DSBSC-волны такая же, как и у AM-волны, и она равна удвоенной частоте модулирующего сигнала.
Расчет мощности волны DSBSC
Рассмотрим следующее уравнение модулированной волны DSBSC.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
Мощность волны DSBSC равна сумме мощностей частотных составляющих верхней и нижней боковой полосы.
$$ P_t = P_ {USB} + P_ {LSB} $$
Мы знаем, что стандартная формула мощности сигнала cos:
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R} $$
Во-первых, давайте по очереди найдем мощности верхней и нижней боковых полос.
Мощность верхней боковой полосы
$$ P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
Точно так же мы получим мощность нижней боковой полосы, такую же, как мощность верхней боковой полосы.
$$ P_ {USB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
Теперь давайте сложим эти две мощности боковой полосы, чтобы получить мощность волны DSBSC.
$$ P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} + \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$
$$ \ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R} $$
Следовательно, мощность, необходимая для передачи волны DSBSC, равна мощности обеих боковых полос.
В этой главе давайте обсудим модуляторы, которые генерируют волны DSBSC. Следующие два модулятора генерируют волну DSBSC.
- Сбалансированный модулятор
- Кольцевой модулятор
Сбалансированный модулятор
Ниже представлена блок-схема сбалансированного модулятора.

Balanced modulatorсостоит из двух идентичных модуляторов AM. Эти два модулятора расположены в сбалансированной конфигурации для подавления несущего сигнала. Следовательно, он называется сбалансированным модулятором.
Один и тот же несущий сигнал $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $ применяется в качестве одного из входов для этих двух модуляторов AM. Модулирующий сигнал $ m \ left (t \ right) $ подается в качестве другого входа в верхний модулятор AM. В то время как модулирующий сигнал $ m \ left (t \ right) $ с противоположной полярностью, то есть $ -m \ left (t \ right) $, подается в качестве другого входа в нижний модулятор AM.
Выходной сигнал верхнего модулятора AM
$$ s_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Выход нижнего модулятора AM
$$ s_2 \ left (t \ right) = A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
Мы получаем DSBSC-волну $ s \ left (t \ right) $, вычитая $ s_2 \ left (t \ right) $ из $ s_1 \ left (t \ right) $. Летний блок используется для выполнения этой операции. $ s_1 \ left (t \ right) $ с положительным знаком и $ s_2 \ left (t \ right) $ с отрицательным знаком применяются в качестве входных данных для летнего блока. Таким образом, летний блок дает результат $ s \ left (t \ right) $, который является разностью $ s_1 \ left (t \ right) $ и $ s_2 \ left (t \ right) $.
$$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - A_c \ cos \ left (2 \ pi f_ct \ right) + $$
$ A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $
Мы знаем, что стандартное уравнение волны DSBSC:
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
Сравнивая выход летнего блока со стандартным уравнением волны DSBSC, мы получим коэффициент масштабирования как $ 2k_a $
Кольцевой модулятор
Ниже представлена блок-схема кольцевого модулятора.

На этой схеме четыре диода $ D_1 $, $ D_2 $, $ D_3 $ и $ D_4 $ соединены в кольцевую структуру. Следовательно, этот модулятор называетсяring modulator. На этой схеме используются два трансформатора с центральным ответвлением. Сигнал сообщения $ m \ left (t \ right) $ подается на входной трансформатор. Между тем, несущие сигналы $ c \ left (t \ right) $ применяются между двумя центральными трансформаторами.
При положительном полупериоде несущего сигнала диоды $ D_1 $ и $ D_3 $ включаются, а два других диода $ D_2 $ и $ D_4 $ выключаются. В этом случае сигнал сообщения умножается на +1.
Для отрицательного полупериода несущего сигнала диоды $ D_2 $ и $ D_4 $ включаются, а два других диода $ D_1 $ и $ D_3 $ выключаются. В этом случае сигнал сообщения умножается на -1. Это приводит к сдвигу фазы на $ 180 ^ 0 $ в результирующей волне DSBSC.
Из приведенного выше анализа можно сказать, что четыре диода $ D_1 $, $ D_2 $, $ D_3 $ и $ D_4 $ управляются сигналом несущей. Если носитель представляет собой прямоугольную волну, то представление ряда Фурье $ c \ left (t \ right) $ представляется в виде
$$ c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] $$
Мы получим DSBSC-волну $ s \ left (t \ right) $, которая является просто произведением несущего сигнала $ c \ left (t \ right) $ и сигнала сообщения $ m \ left (t \ right) $ ie. ,
$$ s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] m \ left (t \ right) $$
Вышеприведенное уравнение представляет волну DSBSC, которая получается на выходном трансформаторе кольцевого модулятора.
Модуляторы DSBSC также называют product modulators поскольку они производят выходной сигнал, который является продуктом двух входных сигналов.
Процесс извлечения исходного сигнала сообщения из волны DSBSC известен как обнаружение или демодуляция DSBSC. Следующие демодуляторы (детекторы) используются для демодуляции волны DSBSC.
- Когерентный детектор
- Костас Петля
Когерентный детектор
Здесь тот же сигнал несущей (который используется для генерации сигнала DSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называетсяcoherent или же synchronous detection. Ниже представлена блок-схема когерентного детектора.

В этом процессе сигнал сообщения может быть извлечен из волны DSBSC путем умножения его на несущую, имеющую ту же частоту и фазу несущей, которые используются в модуляции DSBSC. Результирующий сигнал затем проходит через фильтр нижних частот. Выход этого фильтра - желаемый сигнал сообщения.
Пусть волна DSBSC будет
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
Выход гетеродина равен
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
Где, $ \ phi $ - разность фаз между сигналом гетеродина и сигналом несущей, который используется для модуляции DSBSC.
На рисунке мы можем записать выходной сигнал модулятора продукта как
$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c \ left (t \ right) $ в приведенное выше уравнение.
$$ \ Rightarrow v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
$ = {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ left (t \ right) $
$ = \ frac {{A_ {c}} ^ {2}} {2} \ left [\ cos \ left (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ left (t \ справа) $
$$ v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$
В приведенном выше уравнении первый член - это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот.
Следовательно, выходной сигнал фильтра нижних частот равен
$$ v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) $$
Амплитуда демодулированного сигнала будет максимальной, когда $ \ phi = 0 ^ 0 $. Поэтому сигнал гетеродина и сигнал несущей должны быть синфазными, то есть между этими двумя сигналами не должно быть разности фаз.
Амплитуда демодулированного сигнала будет равна нулю, когда $ \ phi = \ pm 90 ^ 0 $. Этот эффект называетсяquadrature null effect.
Костас Петля
Петля Костаса используется, чтобы синхронизировать по фазе и несущий сигнал (используемый для модуляции DSBSC), и локально сгенерированный сигнал. Ниже приведена блок-схема цикла Костаса.

Costas loopсостоит из двух модуляторов продукта с общим входом $ s \ left (t \ right) $, который является волной DSBSC. Другой ввод для обоих модуляторов продукта берется изVoltage Controlled Oscillator (VCO) с фазовым сдвигом $ -90 ^ 0 $ на одном из модулятора продукта, как показано на рисунке.
Мы знаем, что уравнение волны DSBSC имеет вид
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
Пусть выход VCO будет
$$ c_1 \ left (t \ right) = \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
Этот выход ГУН используется как вход несущей для модулятора верхнего продукта.
Следовательно, выходной сигнал модулятора верхнего продукта равен
$$ v_1 \ left (t \ right) = s \ left (t \ right) c_1 \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c_1 \ left (t \ right) $ в приведенное выше уравнение.
$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $
После упрощения мы получим $ v_1 \ left (t \ right) $ как
$$ v_1 \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) + \ frac {A_c} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$
Этот сигнал подается на вход верхнего фильтра нижних частот. Выход этого фильтра нижних частот
$$ v_ {01} \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) $$
Следовательно, выходной сигнал этого фильтра нижних частот является масштабированной версией модулирующего сигнала.
Выход фазовращателя $ -90 ^ 0 $ равен
$$ c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right) $$
Этот сигнал применяется как вход несущей модулятора нижнего продукта.
Выходной сигнал модулятора нижнего продукта равен
$$ v_2 \ left (t \ right) = s \ left (t \ right) c_2 \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c_2 \ left (t \ right) $ в приведенное выше уравнение.
$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $
После упрощения мы получим $ v_2 \ left (t \ right) $ как
$$ v_2 \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) + \ frac {A_c} {2} \ sin \ left (4 \ pi f_ct + \ фи \ право) м \ влево (т \ право) $$
Этот сигнал подается на вход нижнего фильтра нижних частот. Выход этого фильтра нижних частот
$$ v_ {02} \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) $$
Выход этого фильтра нижних частот имеет разность фаз $ -90 ^ 0 $ с выходом фильтра верхних частот нижних частот.
Выходы этих двух фильтров нижних частот используются как входы фазового дискриминатора. На основе разности фаз между этими двумя сигналами фазовый дискриминатор выдает управляющий сигнал постоянного тока.
Этот сигнал подается на вход ГУН для исправления фазовой ошибки на выходе ГУН. Следовательно, несущий сигнал (используемый для модуляции DSBSC) и локально сгенерированный сигнал (выход VCO) находятся в фазе.
В предыдущих главах мы обсуждали модуляцию и демодуляцию DSBSC. Модулированный сигнал DSBSC имеет две боковые полосы. Поскольку две боковые полосы несут одинаковую информацию, нет необходимости передавать обе боковые полосы. Мы можем удалить одну боковую полосу.
Процесс подавления одной из боковых полос вместе с несущей и передачи одной боковой полосы называется Single Sideband Suppressed Carrier система или просто SSBSC. Он построен, как показано на следующем рисунке.

На рисунке выше несущая и нижняя боковая полоса подавлены. Следовательно, для передачи используется верхняя боковая полоса. Точно так же мы можем подавить несущую и верхнюю боковую полосу при передаче нижней боковой полосы.
Эта система SSBSC, которая передает одну боковую полосу, имеет высокую мощность, поскольку мощность, выделенная как для несущей, так и для другой боковой полосы, используется при передаче этой одной боковой полосы.
Математические выражения
Давайте рассмотрим те же математические выражения для модулирующего и несущего сигналов, которые мы рассматривали в предыдущих главах.
т.е. модулирующий сигнал
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
Несущий сигнал
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Математически мы можем представить уравнение волны SSBSC как
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ для верхней боковой полосы
Или же
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ для нижней боковой полосы
Полоса пропускания SSBSC волны
Мы знаем, что модулированная волна DSBSC содержит две боковые полосы и ее ширина составляет $ 2f_m $. Поскольку модулированная волна SSBSC содержит только одну боковую полосу, ее полоса пропускания составляет половину полосы пропускания модулированной волны DSBSC.
т.е. Bandwidth of SSBSC modulated wave = $ \ frac {2f_m} {2} = f_m $
Следовательно, ширина полосы модулированной волны SSBSC равна $ f_m $ и равна частоте модулирующего сигнала.
Расчет мощности волны SSBSC
Рассмотрим следующее уравнение модулированной волны SSBSC.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ для верхней боковой полосы
Или же
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ для нижней боковой полосы
Мощность волны SSBSC равна мощности любой частотной составляющей одной боковой полосы.
$$ P_t = P_ {USB} = P_ {LSB} $$
Мы знаем, что стандартная формула для мощности сигнала cos
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R} $$
В этом случае мощность верхней боковой полосы равна
$$ P_ {USB} = \ frac {\ left (A_m A_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$
Точно так же мы получим мощность нижней боковой полосы, такую же, как мощность верхней боковой полосы.
$$ P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
Следовательно, мощность волны SSBSC равна
$$ P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
Преимущества
Занятая полоса пропускания или пространство спектра меньше, чем волны AM и DSBSC.
Допускается передача большего количества сигналов.
Энергия сохраняется.
Может передаваться сигнал высокой мощности.
Присутствует меньше шума.
Затухание сигнала менее вероятно.
Недостатки
Генерация и обнаружение волны SSBSC - сложный процесс.
Если SSB-передатчик и приемник не обладают отличной стабильностью частоты, качество сигнала ухудшается.
Приложения
Для требований энергосбережения и низкой пропускной способности.
В наземной, воздушной и морской мобильной связи.
В двухточечной связи.
В радиосвязи.
В телевидении, телеметрии и радиолокационной связи.
В военной связи, например, в любительском радио и т. Д.
В этой главе давайте обсудим модуляторы, которые генерируют волны SSBSC. Мы можем сгенерировать волну SSBSC, используя следующие два метода.
- Метод частотной дискриминации
- Метод фазовой дискриминации
Метод частотной дискриминации
На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода частотной дискриминации.

В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входа полосового фильтра. Этот полосовой фильтр производит на выходе волну SSBSC.
Выберите частотный диапазон полосового фильтра как спектр желаемой волны SSBSC. Это означает, что полосовой фильтр может быть настроен на частоту верхней или нижней боковой полосы, чтобы получить соответствующую волну SSBSC, имеющую верхнюю или нижнюю боковую полосу.
Метод фазовой дискриминации
На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода фазовой дискриминации.

Эта блок-схема состоит из двух модуляторов продукта, двух фазовращателей $ -90 ^ 0 $, одного гетеродина и одного летнего блока. Модулятор продукта производит выходной сигнал, который является произведением двух входов. Фазовращатель $ -90 ^ 0 $ выдает выходной сигнал с фазовой задержкой $ -90 ^ 0 $ относительно входа.
Локальный генератор используется для генерации несущего сигнала. Блок Summer выдает выходной сигнал, который является либо суммой двух входов, либо разностью двух входов в зависимости от полярности входов.
Модулирующий сигнал $ A_m \ cos \ left (2 \ pi f_mt \ right) $ и сигнал несущей $ A_c \ cos \ left (2 \ pi f_ct \ right) $ напрямую подаются в качестве входов в модулятор верхнего произведения. Таким образом, модулятор верхнего продукта производит выходной сигнал, который является продуктом этих двух входов.
Выход модулятора верхнего продукта:
$$ s_1 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} $$
Модулирующий сигнал $ A_m \ cos \ left (2 \ pi f_mt \ right) $ и сигнал несущей $ A_c \ cos \ left (2 \ pi f_ct \ right) $ сдвигаются по фазе на $ -90 ^ 0 $ перед применением как входы в модулятор нижнего продукта. Таким образом, модулятор нижнего продукта производит выходной сигнал, который является продуктом этих двух входов.
Выход модулятора нижнего продукта составляет
$$ s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right) $$
$ \ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ влево (f_c + f_m \ right) t \ right] \ right \} $
Добавьте $ s_1 \ left (t \ right) $ и $ s_2 \ left (t \ right) $, чтобы получить модулированную SSBSC волну $ s \ left (t \ right) $ с нижней боковой полосой.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} + $
$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ right \} $
$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
Вычтите $ s_2 \ left (t \ right) $ из $ s_1 \ left (t \ right) $, чтобы получить модулированную SSBSC волну $ s \ left (t \ right) $, имеющую верхнюю боковую полосу.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} - $
$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ right \} $
$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $
Следовательно, правильно подобрав полярности входов на летнем блоке, мы получим волну SSBSC, имеющую верхнюю или нижнюю боковую полосу.
Процесс извлечения исходного сигнала сообщения из волны SSBSC известен как обнаружение или демодуляция SSBSC. Когерентный детектор используется для демодуляции волны SSBSC.
Когерентный детектор
Здесь тот же несущий сигнал (который используется для генерации волны SSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называетсяcoherent или же synchronous detection. Ниже представлена блок-схема когерентного детектора.

В этом процессе сигнал сообщения может быть извлечен из волны SSBSC путем умножения его на несущую, имеющую ту же частоту и фазу несущей, которые используются в модуляции SSBSC. Результирующий сигнал затем проходит через фильтр нижних частот. Выход этого фильтра - сигнал желаемого сообщения.
Рассмотрим следующее SSBSC волна, имеющая lower sideband.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
Выход гетеродина равен
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
На рисунке мы можем записать выходной сигнал модулятора продукта как
$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c \ left (t \ right) $ в приведенное выше уравнение.
$$ v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ right) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ right) t \ right \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] $
В приведенном выше уравнении первый член - это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот.
Следовательно, выходной сигнал фильтра нижних частот равен
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
Здесь коэффициент масштабирования равен $ \ frac {{A_ {c}} ^ {2}} {4} $.
Мы можем использовать ту же блок-схему для демодуляции волны SSBSC, имеющей верхнюю боковую полосу. Рассмотрим следующееSSBSC волна, имеющая upper sideband.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $$
Выход гетеродина равен
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Мы можем записать выходной сигнал модулятора продукта как
$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c \ left (t \ right) $ в приведенное выше уравнение.
$$ \ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ right) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] $
В приведенном выше уравнении первый член - это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот.
Следовательно, выходной сигнал фильтра нижних частот равен
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
Здесь также коэффициент масштабирования равен $ \ frac {{A_ {c}} ^ {2}} {4} $.
Следовательно, мы получаем одинаковый демодулированный выходной сигнал в обоих случаях, используя когерентный детектор.
В предыдущих главах мы обсуждали модуляцию SSBSC и демодуляцию. Модулированный сигнал SSBSC имеет только одну частоту боковой полосы. Теоретически мы можем полностью получить одну частотную составляющую боковой полосы, используя идеальный полосовой фильтр. Однако практически мы не можем получить всю частотную составляющую боковой полосы. Из-за этого теряется некоторая информация.
Чтобы избежать этой потери, выбран метод, являющийся компромиссом между DSBSC и SSBSC. Этот метод известен какVestigial Side Band Suppressed Carrier (VSBSC)техника. Слово «остаток» означает «часть», от которой и произошло название.
VSBSC Modulationэто процесс, при котором часть сигнала, называемая следом, модулируется вместе с одной боковой полосой. Частотный спектр волны VSBSC показан на следующем рисунке.

Наряду с верхней боковой полосой, в этом методе передается также часть нижней боковой полосы. Точно так же мы можем передавать нижнюю боковую полосу вместе с частью верхней боковой полосы. Защитная полоса очень маленькой ширины проложена по обе стороны от VSB, чтобы избежать помех. Модуляция VSB в основном используется в телевизионных передачах.
Полоса пропускания модуляции VSBSC
Мы знаем, что ширина полосы модулированной волны SSBSC равна $ f_m $. Поскольку модулированная волна VSBSC содержит частотные компоненты одной боковой полосы вместе с остатком другой боковой полосы, ширина полосы частот будет суммой ширины полосы модулированной волны SSBSC и остаточной частоты $ f_v $.
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
Преимущества
Ниже приведены преимущества модуляции VSBSC.
Очень эффективным.
Уменьшение полосы пропускания по сравнению с волнами AM и DSBSC.
Конструкция фильтра проста, поскольку не требуется высокой точности.
Передача низкочастотных компонентов возможна без каких-либо затруднений.
Обладает хорошими фазовыми характеристиками.
Недостатки
Ниже приведены недостатки модуляции VSBSC.
Пропускная способность больше по сравнению с волной SSBSC.
Демодуляция сложна.
Приложения
Наиболее известное и стандартное применение VSBSC - это передача телевизионных сигналов. Кроме того, это наиболее удобный и эффективный метод с учетом использования полосы пропускания.
Теперь давайте обсудим модулятор, который генерирует волны VSBSC, и демодулятор, который демодулирует волны VSBSC один за другим.
Генерация VSBSC
Генерация волны VSBSC аналогична генерации волны SSBSC. Модулятор VSBSC показан на следующем рисунке.
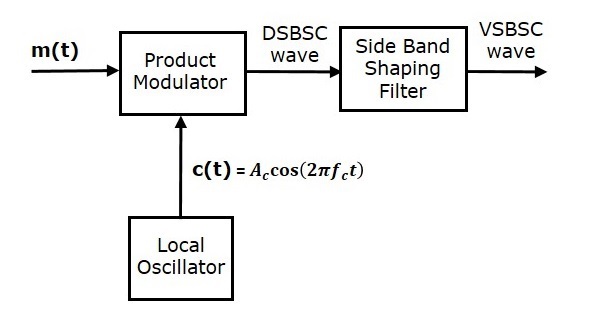
В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входного сигнала фильтра формирования боковой полосы. Этот фильтр производит выходной сигнал, представляющий собой волну VSBSC.
Модулирующий сигнал $ m \ left (t \ right) $ и сигнал несущей $ A_c \ cos \ left (2 \ pi f_ct \ right) $ используются в качестве входных сигналов для модулятора произведения. Следовательно, модулятор продукта выдает выходной сигнал, который является произведением этих двух входов.
Следовательно, выходной сигнал модулятора продукта равен
$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
Примените преобразование Фурье с обеих сторон
$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$
Вышеприведенное уравнение представляет собой уравнение частотного спектра DSBSC.
Пусть передаточная функция фильтра формирования боковой полосы равна $ H \ left (f \ right) $. Этот фильтр имеет вход $ p \ left (t \ right) $, а выход - модулированную VSBSC волну $ s \ left (t \ right) $. Преобразования Фурье $ p \ left (t \ right) $ и $ s \ left (t \ right) $ равны $ P \ left (t \ right) $ и $ S \ left (t \ right) $ соответственно.
Математически мы можем записать $ S \ left (f \ right) $ как
$$ S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right) $$
Подставьте значение $ P \ left (f \ right) $ в приведенное выше уравнение.
$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right) $$
Вышеприведенное уравнение представляет собой уравнение частотного спектра VSBSC.
Демодуляция VSBSC
Демодуляция волны VSBSC аналогична демодуляции волны SSBSC. Здесь тот же несущий сигнал (который используется для генерации волны VSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называетсяcoherent или же synchronous detection. Демодулятор VSBSC показан на следующем рисунке.

В этом процессе сигнал сообщения может быть извлечен из волны VSBSC путем умножения его на несущую, которая имеет ту же частоту и фазу несущей, которые используются в модуляции VSBSC. Результирующий сигнал затем проходит через фильтр нижних частот. Выход этого фильтра - желаемый сигнал сообщения.
Пусть волна VSBSC будет $ s \ left (t \ right) $, а сигнал несущей - $ A_c \ cos \ left (2 \ pi f_ct \ right) $.
На рисунке мы можем записать выходной сигнал модулятора продукта как
$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$
Примените преобразование Фурье с обеих сторон
$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$
Мы знаем, что $ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ влево (f \ right) $
Из приведенного выше уравнения найдем $ S \ left (f-f_c \ right) $ и $ S \ left (f + f_c \ right) $.
$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ right] H \ left (f-f_c \ right) $$
$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right) $
$$ S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ right] H \ left (f + f_c \ right) $$
$ \ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right) $
Замените значения $ S \ left (f-f_c \ right) $ и $ S \ left (f + f_c \ right) $ в $ V \ left (f \ right) $.
$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $
$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $
$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ влево (f + f_c \ right) \ right] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ right) H \ left (f + f_c \ right) \ right] $
В приведенном выше уравнении первый член представляет масштабированную версию частотного спектра сигнала полезного сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот.
$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $$
Другой тип модуляции при непрерывной модуляции - это Angle Modulation. Угловая модуляция - это процесс, при котором частота или фаза несущего сигнала изменяется в соответствии с сигналом сообщения.
Стандартное уравнение волны с угловой модуляцией:
$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$
Где,
$ A_c $ - это амплитуда модулированной волны, которая совпадает с амплитудой несущего сигнала.
$ \ theta _i \ left (t \ right) $ - угол модулированной волны
Угловая модуляция подразделяется на частотную модуляцию и фазовую модуляцию.
Frequency Modulation представляет собой процесс изменения частоты несущего сигнала линейно с сигналом сообщения.
Phase Modulation - это процесс линейного изменения фазы несущего сигнала в зависимости от сигнала сообщения.
Теперь давайте обсудим их подробно.
Модуляция частоты
При амплитудной модуляции изменяется амплитуда несущего сигнала. Тогда как вFrequency Modulation (FM), частота несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.
Следовательно, при частотной модуляции амплитуда и фаза несущего сигнала остаются постоянными. Это можно лучше понять, наблюдая за следующими рисунками.
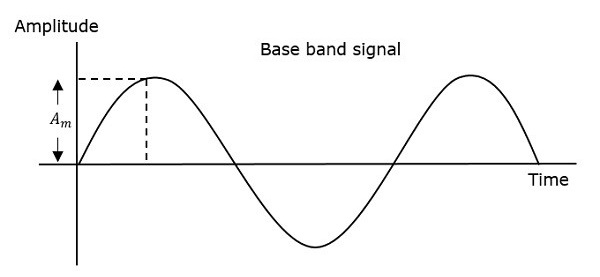


Частота модулированной волны увеличивается, когда увеличивается амплитуда модулирующего сигнала или сигнала сообщения. Точно так же частота модулированной волны уменьшается, когда уменьшается амплитуда модулирующего сигнала. Обратите внимание, что частота модулированной волны остается постоянной и равна частоте несущего сигнала, когда амплитуда модулирующего сигнала равна нулю.
Математическое представление
Уравнение для мгновенной частоты $ f_i $ при модуляции FM имеет вид
$$ f_i = f_c + k_fm \ left (t \ right) $$
Где,
$ f_c $ - несущая частота
$ k_t $ - частотная чувствительность
$ m \ left (t \ right) $ - сигнал сообщения
Нам известна связь между угловой частотой $ \ omega_i $ и углом $ \ theta _i \ left (t \ right) $ как
$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$
$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $
Подставьте значение $ f_i $ в приведенное выше уравнение.
$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $$
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $
Подставьте значение $ \ theta _i \ left (t \ right) $ в стандартное уравнение волны с угловой модуляцией.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
Это equation of FM wave.
Если модулирующий сигнал равен $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, то уравнение FM-волны будет
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
Где,
$ \ beta $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $
Разница между модулированной частотой FM (мгновенной частотой) и нормальной несущей частотой называется Frequency Deviation. Он обозначается $ \ Delta f $, что равно произведению $ k_f $ и $ A_m $.
FM можно разделить на Narrowband FM и Wideband FM на основе значений индекса модуляции $ \ beta $.
Узкополосный FM
Ниже приведены особенности Narrowband FM.
Эта частотная модуляция имеет небольшую полосу пропускания по сравнению с широкополосной ЧМ.
Индекс модуляции $ \ beta $ небольшой, т.е. меньше 1.
Его спектр состоит из несущей, верхней и нижней боковых полос.
Это используется в мобильной связи, такой как полицейская беспроводная связь, машины скорой помощи, такси и т. Д.
Широкополосный FM
Ниже приведены особенности широкополосного FM.
Эта частотная модуляция имеет бесконечную полосу пропускания.
Индекс модуляции $ \ beta $ велик, т.е. больше 1.
Его спектр состоит из несущей и бесконечного числа боковых полос, расположенных вокруг нее.
Это используется в развлекательных, вещательных приложениях, таких как FM-радио, телевидение и т. Д.
Фазовая модуляция
При частотной модуляции частота несущей меняется. Тогда как вPhase Modulation (PM), фаза несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.
Таким образом, при фазовой модуляции амплитуда и частота несущего сигнала остаются постоянными. Это можно лучше понять, наблюдая за следующими рисунками.
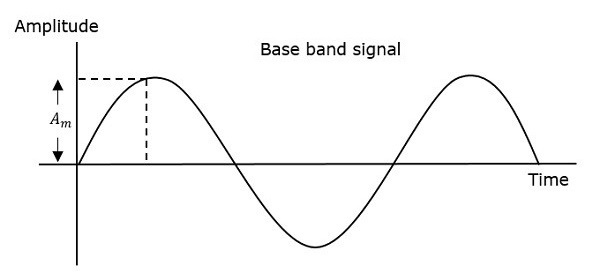

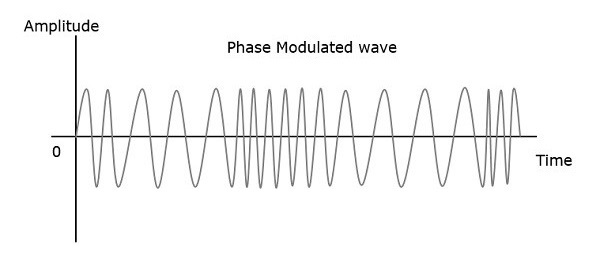
Фаза модулированной волны имеет бесконечное количество точек, где может иметь место фазовый сдвиг в волне. Мгновенная амплитуда модулирующего сигнала изменяет фазу несущего сигнала. Когда амплитуда положительная, фаза изменяется в одном направлении, а если амплитуда отрицательная, фаза изменяется в противоположном направлении.
Математическое представление
Уравнение для мгновенной фазы $ \ phi_i $ при фазовой модуляции имеет вид
$$ \ phi _i = k_p m \ left (t \ right) $$
Где,
$ k_p $ - фазовая чувствительность
$ m \ left (t \ right) $ - сигнал сообщения
Стандартное уравнение волны с угловой модуляцией:
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$
Подставьте значение $ \ phi_i $ в приведенное выше уравнение.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right) $$
Это equation of PM wave.
Если модулирующий сигнал, $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, то уравнение PM волны будет
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right) $$
Где,
$ \ beta $ = modulation index = $ \ Delta \ phi = k_pA_m $
$ \ Delta \ phi $ - отклонение фазы
Фазовая модуляция используется в системах мобильной связи, а частотная модуляция используется в основном для FM-вещания.
В предыдущей главе мы обсудили параметры, используемые в модуляции угла. У каждого параметра своя формула. Используя эти формулы, мы можем найти соответствующие значения параметров. В этой главе давайте решим несколько задач, основанных на концепции частотной модуляции.
Проблема 1
Синусоидальный модулирующий сигнал амплитудой 5 В и частотой 2 кГц подается на ЧМ-генератор, который имеет частотную чувствительность 40 Гц / вольт. Рассчитайте отклонение частоты, индекс модуляции и полосу пропускания.
Решение
Учитывая, что амплитуда модулирующего сигнала, $ A_m = 5V $
Частота модулирующего сигнала, $ f_m = 2 кГц $
Частотная чувствительность, $ k_f = 40 Гц / вольт $
Мы знаем формулу отклонения частоты как
$$ \ Delta f = k_f A_m $$
Подставьте значения $ k_f $ и $ A_m $ в приведенную выше формулу.
$$ \ Delta f = 40 \ times 5 = 200 Гц $$
Следовательно, frequency deviation, $ \ Delta f $ составляет 200 Гц $
Формула для индекса модуляции:
$$ \ beta = \ frac {\ Delta f} {f_m} $$
Подставьте значения $ \ Delta f $ и $ f_m $ в приведенную выше формулу.
$$ \ beta = \ frac {200} {2 \ times 1000} = 0,1 $$
Здесь значение modulation index, $ \ beta $ равно 0,1, что меньше единицы. Следовательно, это узкополосный FM.
Формула для ширины полосы узкополосного FM такая же, как и для AM волны.
$$ BW = 2f_m $$
Подставьте значение $ f_m $ в приведенную выше формулу.
$$ BW = 2 \ times 2K = 4KHz $$
Следовательно bandwidth узкополосной FM-волны составляет 4 кГц.
Проблема 2
Волна FM задается формулой $ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right ) $. Рассчитайте отклонение частоты, полосу пропускания и мощность FM-волны.
Решение
Учитывая, что уравнение FM-волны как
$$ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right) $$
Мы знаем стандартное уравнение FM-волны как
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
Мы получим следующие значения, сравнив два приведенных выше уравнения.
Амплитуда несущего сигнала, $ A_c = 20V $
Частота несущего сигнала, $ f_c = 4 \ times 10 ^ 6 Гц = 4 МГц $
Частота сигнала сообщения, $ f_m = 1 \ times 10 ^ 3 Гц = 1 кГц $
Индекс модуляции, $ \ beta = 9 $
Здесь значение индекса модуляции больше единицы. Следовательно, этоWide Band FM.
Мы знаем формулу для индекса модуляции как
$$ \ beta = \ frac {\ Delta f} {f_m} $$
Измените приведенное выше уравнение следующим образом.
$$ \ Delta = \ beta f_m $$
Подставьте значения $ \ beta $ и $ f_m $ в приведенное выше уравнение.
$$ \ Delta = 9 \ times 1K = 9 кГц $$
Следовательно, frequency deviation, $ \ Delta f $ составляет $ 9 кГц $.
Формула для ширины полосы широкополосной FM-волны:
$$ BW = 2 \ left (\ beta +1 \ right) f_m $$
Подставьте значения $ \ beta $ и $ f_m $ в приведенную выше формулу.
$$ BW = 2 \ left (9 +1 \ right) 1K = 20KHz $$
Следовательно bandwidth широкополосной FM-волны составляет $ 20 кГц $
Формула мощности FM-волны:
$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$
Предположим, что $ R = 1 \ Omega $, и подставим значение $ A_c $ в приведенное выше уравнение.
$$ P = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$
Следовательно power FM волны - 200 $ watts.
В этой главе давайте обсудим модуляторы, которые генерируют волны NBFM и WBFM. Во-первых, давайте обсудим генерацию NBFM.
Генерация NBFM
Мы знаем, что стандартное уравнение FM-волны имеет вид
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) - $
$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $
Для NBFM,
$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$
Мы знаем, что $ \ cos \ theta \ приблизительно 1 $ и $ \ sin \ theta \ приблизительно 1 $, когда $ \ theta $ очень мало.
Используя указанные выше отношения, мы получим NBFM equation в виде
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ справа) dt $$
Блок-схема модулятора NBFM показана на следующем рисунке.
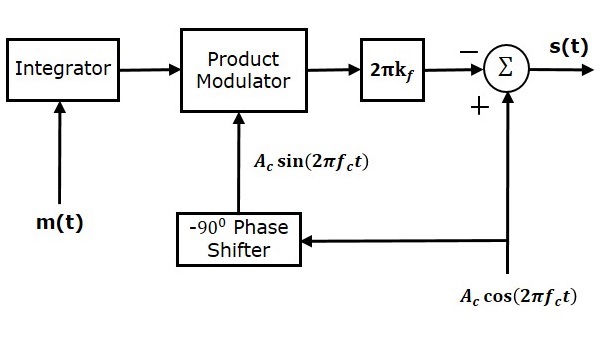
Здесь интегратор используется для интегрирования модулирующего сигнала $ m \ left (t \ right) $. Несущий сигнал $ A_c \ cos \ left (2 \ pi f_ct \ right) $ представляет собой фазу, сдвинутую на $ -90 ^ 0 $, чтобы получить $ A_c \ sin \ left (2 \ pi f_ct \ right) $ с помощью $ -90 ^ 0 $ фазовращатель. Модулятор произведения имеет два входа $ \ int m \ left (t \ right) dt $ и $ A_c \ sin \ left (2 \ pi f_ct \ right) $. Он производит результат, который является продуктом этих двух входов.
Далее это умножается на $ 2 \ pi k_f $, помещая блок $ 2 \ pi k_f $ в прямой путь. Летний блок имеет два входа, которые представляют собой не что иное, как два члена уравнения NBFM. Положительный и отрицательный знаки присваиваются несущему сигналу и другому члену на входе летнего блока. Наконец, летний блок дает волну NBFM.
Генерация WBFM
Следующие два метода генерируют волну WBFM.
- Прямой метод
- Косвенный метод
Прямой метод
Этот метод называется прямым методом, потому что мы напрямую генерируем широкополосную FM-волну. В этом методе для генерации WBFM используется генератор, управляемый напряжением (VCO). ГУН выдает выходной сигнал, частота которого пропорциональна напряжению входного сигнала. Это похоже на определение FM-волны. Блок-схема генерации WBFM-волны показана на следующем рисунке.

Здесь модулирующий сигнал $ m \ left (t \ right) $ подается на вход генератора, управляемого напряжением (ГУН). VCO производит выходной сигнал, который представляет собой не что иное, как WBFM.
$$ f_i \: \ alpha \: m \ left (t \ right) $$
$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $$
Где,
$ f_i $ - мгновенная частота волны WBFM.
Косвенный метод
Этот метод называется косвенным, потому что мы косвенно генерируем широкополосную FM-волну. Это означает, что сначала мы сгенерируем волну NBFM, а затем с помощью умножителей частоты мы получим волну WBFM. Блок-схема генерации WBFM-волны показана на следующем рисунке.

Эта блок-схема состоит в основном из двух этапов. На первом этапе волна NBFM будет сгенерирована с помощью модулятора NBFM. Мы видели блок-схему модулятора NBFM в начале этой главы. Мы знаем, что индекс модуляции волны NBFM меньше единицы. Следовательно, чтобы получить требуемый индекс модуляции (больше единицы) FM-волны, правильно выберите значение множителя частоты.
Frequency multiplierпредставляет собой нелинейное устройство, которое производит выходной сигнал, частота которого в n раз превышает частоту входного сигнала. Где n - коэффициент умножения.
Если волна NBFM, индекс модуляции которой $ \ beta $ меньше 1, применяется в качестве входа умножителя частоты, то умножитель частоты создает выходной сигнал, индекс модуляции которого равен n умножить на $ \ beta $, а частота также равна n. 'умноженная на частоту волны WBFM.
Иногда нам может потребоваться несколько ступеней умножителя частоты и смесителей, чтобы увеличить девиацию частоты и индекс модуляции FM-волны.
В этой главе давайте обсудим демодуляторы, которые демодулируют FM-волну. Следующие два метода демодулируют FM-волну.
- Метод частотной дискриминации
- Метод фазовой дискриминации
Метод частотной дискриминации
Мы знаем, что уравнение FM-волны имеет вид
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
Продифференцируйте указанное выше уравнение относительно 't'.
$$ \ frac {ds \ left (t \ right)} {dt} = -A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
Мы можем записать $ - \ sin \ theta $ как $ \ sin \ left (\ theta -180 ^ 0 \ right) $.
$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right) $$
$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c \ right) \ left [1+ \ left (\ frac {k_f} {k_c} \ right) m \ left ( t \ right) \ right] \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right) $$
В приведенном выше уравнении член амплитуды напоминает огибающую AM волны, а член угла напоминает угол FM волны. Здесь нашим требованием является модулирующий сигнал $ m \ left (t \ right) $. Следовательно, мы можем восстановить его из огибающей AM волны.
На следующем рисунке показана блок-схема FM-демодулятора с использованием метода частотной дискриминации.

Эта блок-схема состоит из дифференциатора и детектора огибающей. Дифференциатор используется для преобразования FM-волны в комбинацию AM-волны и FM-волны. Это означает, что он преобразует частотные вариации FM-волны в соответствующие вариации напряжения (амплитуды) AM-волны. Мы знаем, как работает детектор конвертов. Он производит демодулированный выходной сигнал AM волны, который является не чем иным, как модулирующим сигналом.
Метод фазовой дискриминации
На следующем рисунке показана блок-схема FM-демодулятора с использованием метода фазовой дискриминации.

Эта блок-схема состоит из умножителя, фильтра нижних частот и генератора, управляемого напряжением (ГУН). ГУН выдает выходной сигнал $ v \ left (t \ right) $, частота которого пропорциональна напряжению входного сигнала $ d \ left (t \ right) $. Первоначально, когда сигнал $ d \ left (t \ right) $ равен нулю, отрегулируйте VCO, чтобы получить выходной сигнал $ v \ left (t \ right) $, имеющий несущую частоту и фазовый сдвиг $ -90 ^ 0 $. относительно несущего сигнала.
FM-волна $ s \ left (t \ right) $ и выход VCO $ v \ left (t \ right) $ используются как входы умножителя. Умножитель выдает выходной сигнал с высокочастотной составляющей и низкочастотной составляющей. Фильтр нижних частот устраняет высокочастотную составляющую и производит только низкочастотную составляющую на выходе.
Эта низкочастотная составляющая содержит только относительную разность фаз. Следовательно, мы получаем модулирующий сигнал $ m \ left (t \ right) $ с этого выхода фильтра нижних частот.
Multiplexingэто процесс объединения нескольких сигналов в один сигнал на общей среде. Если аналоговые сигналы мультиплексируются, то это называетсяanalog multiplexing. Точно так же, если цифровые сигналы мультиплексируются, то это называетсяdigital multiplexing.
Мультиплексирование впервые было разработано в телефонии. Несколько сигналов были объединены для передачи по одному кабелю. Процесс мультиплексирования делит канал связи на несколько логических каналов, выделяя каждый для отдельного сигнала сообщения или передаваемого потока данных. Устройство, которое выполняет мультиплексирование, можно назватьMultiplexer или же MUX.
Обратный процесс, т. Е. Извлечение количества каналов из одного, который выполняется на приемнике, называется de-multiplexing. Устройство, которое выполняет демультиплексирование, можно назватьde-multiplexer или же DEMUX.
На следующих рисунках показана концепция MUX и DEMUX. Их основное использование - в области связи.

Типы мультиплексоров
В основном существуют два типа мультиплексоров: аналоговые и цифровые. Далее они подразделяются на мультиплексирование с частотным разделением (FDM), мультиплексирование с разделением по длине волны (WDM) и мультиплексирование с временным разделением (TDM). Следующий рисунок дает подробное представление об этой классификации.
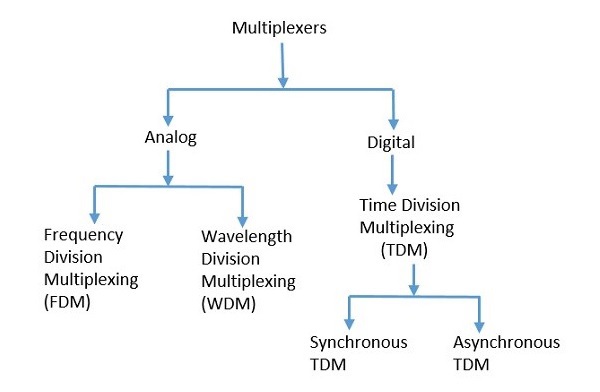
Есть много типов методов мультиплексирования. Из них у нас есть основные типы с общей классификацией, указанные на рисунке выше. Давайте посмотрим на них по отдельности.
Аналоговое мультиплексирование
Сигналы, используемые в методах аналогового мультиплексирования, имеют аналоговую природу. Аналоговые сигналы мультиплексируются в соответствии с их частотой (FDM) или длиной волны (WDM).
Мультиплексирование с частотным разделением
В аналоговом мультиплексировании наиболее часто используемым методом является мультиплексирование с частотным разделением каналов (FDM). В этом методе используются различные частоты для объединения потоков данных и их отправки в среду связи в виде единого сигнала.
Example - Традиционный телевизионный передатчик, который передает несколько каналов по одному кабелю, использует FDM.
Мультиплексирование с разделением по длине волны
Мультиплексирование с разделением по длине волны (WDM) - это аналоговый метод, при котором множество потоков данных с разными длинами волн передаются в световом спектре. Если длина волны увеличивается, частота сигнала уменьшается. Призма, которая может преобразовывать разные длины волн в одну линию, может использоваться на выходе MUX и на входе DEMUX.
Example - В оптоволоконных коммуникациях используется технология WDM, позволяющая объединить волны разных длин в единый световой сигнал для связи.
Цифровое мультиплексирование
Термин цифровой означает дискретные биты информации. Следовательно, доступные данные представлены в виде дискретных кадров или пакетов.
Мультиплексирование с временным разделением
При мультиплексировании с временным разделением (TDM) временной кадр делится на слоты. Этот метод используется для передачи сигнала по одному каналу связи путем выделения одного временного интервала для каждого сообщения.
Мультиплексирование с временным разделением (TDM) можно разделить на синхронный TDM и асинхронный TDM.
Синхронный TDM
В синхронном TDM вход подключен к кадру. Если имеется n соединений, то кадр делится на n временных интервалов. Для каждой входной линии выделяется один слот.
В этом методе частота дискретизации является общей для всех сигналов, и поэтому используется один и тот же тактовый вход. MUX выделяетsame slot к каждому устройству в любое время.
Асинхронный TDM
В асинхронном TDM частота дискретизации для каждого сигнала разная, и общие часы не требуются. Если устройство, назначенное для временного интервала, ничего не передает и бездействует, то этот слот может бытьallotted to another устройство, в отличие от синхронного
Этот тип TDM используется в сетях с асинхронным режимом передачи.
Демультиплексор
Демультиплексоры используются для подключения одного источника к нескольким адресатам. Это процесс, обратный мультиплексированию. Как упоминалось ранее, он используется в основном на приемниках. DEMUX имеет множество приложений. Используется в приемниках в системах связи. Он используется в арифметических и логических устройствах компьютеров для подачи питания, передачи данных и т. Д.
Демультиплексоры используются как преобразователи из последовательного в параллельный. Последовательные данные поступают в DEMUX через равные промежутки времени, и к ним подключается счетчик для управления выходом демультиплексора.
И мультиплексоры, и демультиплексоры играют важную роль в системах связи как в передающей, так и в приемной частях.
В любой системе связи во время передачи сигнала или при приеме сигнала в связь вводится нежелательный сигнал, что делает его неприятным для приемника и ставит под сомнение качество связи. Такое нарушение называетсяNoise.
Что такое шум?
Шум - это unwanted signal, который мешает исходному сигналу сообщения и искажает параметры сигнала сообщения. Это изменение в процессе коммуникации приводит к изменению сообщения. Скорее всего, он поступает на канал или на приемник.
Шумовой сигнал можно понять, взглянув на следующий рисунок.

Следовательно, понятно, что шум - это некоторый сигнал, который не имеет структуры, постоянной частоты или амплитуды. Это довольно случайно и непредсказуемо. Обычно принимаются меры по его снижению, но полностью устранить его не удается.
Наиболее распространенные примеры шума:
Шипящий звук в радиоприемниках
Жужжание во время телефонных разговоров
Мерцание в телевизионных приемниках и т. Д.
Типы шума
Классификация шума выполняется в зависимости от типа источника, эффекта, который он проявляет, или его связи с приемником и т. Д.
Есть два основных способа создания шума. Один через некоторыеexternal source в то время как другой создается internal source, в разделе приемника.
Внешний источник
Этот шум создается внешними источниками, которые обычно могут возникать в среде или канале связи. Этот шум невозможно полностью устранить. Лучший способ - избежать влияния шума на сигнал.
Примеры
Наиболее распространенные примеры этого типа шума:
Атмосферный шум (из-за нарушений в атмосфере).
Внеземной шум, такой как шум солнца и космический шум.
Промышленный шум.
Внутренний источник
Этот шум создается компонентами приемника во время работы. Компоненты в цепях из-за непрерывного функционирования могут создавать несколько типов шума. Этот шум поддается количественной оценке. Правильная конструкция приемника может снизить влияние этого внутреннего шума.
Examples
Наиболее распространенные примеры этого типа шума:
Шум теплового перемешивания (шум Джонсона или электрический шум)
Дробовой шум (из-за случайного движения электронов и дырок)
Временной шум (во время перехода)
Разные шумы - это еще один тип шума, который включает мерцание, эффект сопротивления, шум, создаваемый микшером и т. Д.
Эффекты шума
Шум - это неудобная функция, которая влияет на производительность системы. Ниже приведены эффекты шума.
Шум ограничивает рабочий диапазон систем
Шум косвенно ограничивает самый слабый сигнал, который может усилить усилитель. Генератор в контуре смесителя может ограничивать свою частоту из-за шума. Работа системы зависит от работы ее цепей. Шум ограничивает наименьший сигнал, который приемник способен обработать.
Шум влияет на чувствительность приемников
Чувствительность - это минимальная величина входного сигнала, необходимая для получения выходного сигнала заданного качества. Шум влияет на чувствительность приемной системы, что в конечном итоге влияет на выходной сигнал.
В этой главе давайте вычислим отношение сигнал / шум и показатели качества различных модулированных волн, которые демодулируются в приемнике.
Соотношение сигнал шум
Signal-to-Noise Ratio (SNR)- отношение мощности сигнала к мощности шума. Чем выше значение SNR, тем выше будет качество полученного вывода.
Отношение сигнал / шум в разных точках можно рассчитать по следующим формулам.
Input SNR = $ \ left (SNR \ right) _I = \ frac {Средняя \: \: мощность \: \: of \: \: modulating \: \: signal} {Средняя \: \: мощность \: \: of \: \: шум \: \: at \: \: input} $
Output SNR = $ \ left (SNR \ right) _O = \ frac {Средняя \: \: мощность \: \: of \: \: demodulated \: \: signal} {Средняя \: \: мощность \: \: of \: \: шум \: \: at \: \: output} $
Channel SNR = $ \ left (SNR \ right) _C = \ frac {Средняя \: \: мощность \: \: of \: \: modulated \: \: signal} {Средняя \: \: мощность \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $
Рисунок заслуг
Отношение выходного SNR и входного SNR можно обозначить как Figure of Merit. Обозначается онF. Он описывает производительность устройства.
$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _I} $$
Показатель качества приемника составляет
$$ F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _C} $$
Это потому, что для приемника канал является входом.
Расчет SNR в системе AM
Рассмотрим следующую модель приемника AM-системы для анализа шума.

Мы знаем, что волна с амплитудной модуляцией (AM)
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
Средняя мощность АМ волны составляет
$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$
Средняя мощность шума в полосе пропускания сообщения составляет
$$ P_ {nc} = WN_0 $$
Подставьте эти значения в channel SNR формула
$$ \ left (SNR \ right) _ {C, AM} = \ frac {Средняя \: \: Мощность \: \: of \: \: AM \: \: Wave} {Средняя \: \: Мощность \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0} $$
Где,
P это мощность сигнала сообщения = $ \ frac {{A_ {m}} ^ {2}} {2} $
W это пропускная способность сообщения
Предположим, что полосовой шум смешан с волной AM в канале, как показано на рисунке выше. Эта комбинация применяется на входе демодулятора AM. Следовательно, вход AM-демодулятора.
$$ v \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$ \ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) + $
$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $
$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $
Где $ n_I \ left (t \ right) $ и $ n_Q \ left (t \ right) $ находятся в фазовой и квадратурной фазовых составляющих шума.
Выход AM-демодулятора - это не что иное, как огибающая вышеуказанного сигнала.
$$ d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ right) \ right) ^ 2} $$
$$ \ Rightarrow d \ left (t \ right) \ приблизительно A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) $$
Средняя мощность демодулированного сигнала составляет
$$ P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
Средняя мощность шума на выходе составляет
$$ P_no = WN_0 $$
Подставьте эти значения в output SNR формула.
$$ \ left (SNR \ right) _ {O, AM} = \ frac {Средняя \: \: Мощность \: \: of \: \: demodulated \: \: signal} {Средняя \: \: Мощность \: \: of \: \: noise \: \: at \: \: Output} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
Замените значения в Figure of merit формулы приемника AM.
$$ F = \ frac {\ left (SNR \ right) _ {O, AM}} {\ left (SNR \ right) _ {C, AM}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
Таким образом, добротность AM-приемника меньше единицы.
Расчет SNR в системе DSBSC
Рассмотрим следующую модель приемника системы DSBSC для анализа шума.

Мы знаем, что модулированная волна DSBSC
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
Средняя мощность модулированной волны DSBSC составляет
$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
Средняя мощность шума в полосе пропускания сообщения составляет
$$ P_ {nc} = WN_0 $$
Подставьте эти значения в channel SNR формула.
$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Average \: \: Power \: \: of \: \: DSBSC \: \: modulated \: \: wave} {Среднее \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
Предположим, что полосовой шум смешан с модулированной волной DSBSC в канале, как показано на рисунке выше. Эта комбинация используется как один из входов модулятора продукта. Следовательно, вход этого модулятора продукта
$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $$
$$ \ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
Локальный осциллятор генерирует несущий сигнал $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Этот сигнал используется в качестве другого входа для модулятора продукта. Следовательно, модулятор продукта производит выходной сигнал, который является произведением $ v_1 \ left (t \ right) $ и $ c \ left (t \ right) $.
$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ v_1 \ left (t \ right) $ и $ c \ left (t \ right) $ в приведенное выше уравнение.
$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) ) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$
Когда вышеупомянутый сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как
$$ d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2} $$
Средняя мощность демодулированного сигнала составляет
$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
Средняя мощность шума на выходе составляет
$$ P_ {no} = \ frac {WN_0} {4} $$
Подставьте эти значения в output SNR формула.
$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Средняя \: \: Мощность \: \: of \: \: demodulated \: \: signal} {Средняя \: \: Мощность \: \: of \: \: noise \: \: at \: \: Output} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
Замените значения в Figure of merit формулы приемника DSBSC.
$$ F = \ frac {\ left (SNR \ right) _ {O, DSBSC}} {\ left (SNR \ right) _ {C, DSBSC}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right) $$
$$ \ Rightarrow F = 1 $$
Таким образом, показатель качества приемника DSBSC равен 1.
Расчет SNR в системе SSBSC
Рассмотрим следующую модель приемника системы SSBSC для анализа шума.
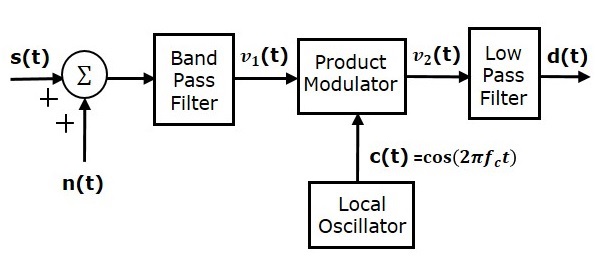
Мы знаем, что модулированная волна SSBSC с нижней боковой полосой является
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
Средняя мощность модулированной волны SSBSC составляет
$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
Средняя мощность шума в полосе пропускания сообщения составляет
$$ P_ {nc} = WN_0 $$
Подставьте эти значения в channel SNR формула.
$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Average \: \: Power \: \: of \: \: SSBSC \: \: modulated \: \: wave} {Среднее \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
Предположим, что полосовой шум смешан с модулированной волной SSBSC в канале, как показано на рисунке выше. Эта комбинация используется как один из входов модулятора продукта. Следовательно, вход этого модулятора продукта
$$ v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right) $$
$$ v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
Локальный осциллятор генерирует несущий сигнал $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $. Этот сигнал применяется в качестве другого входа в модулятор продукта. Следовательно, модулятор продукта производит выходной сигнал, который является произведением $ v_1 \ left (t \ right) $ и $ c \ left (t \ right) $.
$$ v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ v_1 \ left (t \ right) $ и $ c \ left (t \ right) $ в приведенное выше уравнение.
$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) - $
$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ right) + $
$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} + $
$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) - n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $
Когда вышеупомянутый сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как
$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$
Средняя мощность демодулированного сигнала составляет
$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
Средняя мощность шума на выходе составляет
$$ P_ {no} = \ frac {WN_0} {4} $$
Подставьте эти значения в output SNR формула
$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Средняя \: \: Мощность \: \: of \: \: demodulated \: \: signal} {Средняя \: \: Мощность \: \: of \: \: noise \: \: at \: \: output} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
Замените значения в Figure of merit формулы приемника SSBSC
$$ F = \ frac {\ left (SNR \ right) _ {O, SSBSC}} {\ left (SNR \ right) _ {C, SSBSC}} $$
$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) $$
$$ F = 1 $$
Следовательно, добротность приемника SSBSC равна 1.
Антенна, находящаяся в конце секции передатчика, передает модулированную волну. В этой главе давайте обсудим передатчики AM и FM.
AM-передатчик
AM-передатчик принимает аудиосигнал в качестве входа и подает модулированную по амплитуде волну на антенну в качестве выходного сигнала для передачи. Блок-схема AM-передатчика показана на следующем рисунке.

Работу AM-передатчика можно объяснить следующим образом.
Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.
Генератор RF генерирует несущий сигнал.
И модулирующий, и несущий сигнал отправляются на AM-модулятор.
Усилитель мощности используется для увеличения уровней мощности AM волны. Эта волна, наконец, передается на антенну для передачи.
FM-передатчик
FM-передатчик - это целое устройство, которое принимает аудиосигнал в качестве входа и доставляет FM-волну на антенну в качестве выхода для передачи. Блок-схема FM-передатчика показана на следующем рисунке.

Работу FM-передатчика можно объяснить следующим образом.
Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.
Затем этот сигнал передается на фильтр верхних частот, который действует как сеть предыскажений, отфильтровывая шум и улучшая отношение сигнал / шум.
Этот сигнал далее передается в схему модулятора FM.
Схема генератора генерирует высокочастотную несущую, которая отправляется в модулятор вместе с модулирующим сигналом.
Для увеличения рабочей частоты используется несколько ступеней умножителя частоты. Даже тогда мощности сигнала недостаточно для передачи. Следовательно, в конце используется РЧ-усилитель мощности для увеличения мощности модулированного сигнала. Этот FM-модулированный выходной сигнал передается на антенну для передачи.
Антенна, находящаяся в начале секции приемника, принимает модулированную волну. Сначала давайте обсудим требования к ресиверу.
Требования к получателю
Приемник AM принимает волну AM и демодулирует ее с помощью детектора огибающей. Точно так же FM-приемник принимает FM-волну и демодулирует ее, используя метод частотной дискриминации. Ниже приведены требования к приемнику AM и FM.
Это должно быть рентабельным.
Он должен принимать соответствующие модулированные волны.
Приемник должен уметь настраивать и усиливать желаемую станцию.
Он должен иметь возможность отклонять нежелательные станции.
Демодуляция должна выполняться для всех сигналов станции, независимо от частоты несущего сигнала.
Для выполнения этих требований схема тюнера и схема смесителя должны быть очень эффективными. Процедура ВЧ-смешения - интересное явление.
RF смешивание
Блок микширования RF развивает Intermediate Frequency (IF), в который преобразуется любой принятый сигнал для эффективной обработки сигнала.
RF Mixer - важный этап в приемнике. Берутся два сигнала с разными частотами, где один уровень сигнала влияет на уровень другого сигнала, для получения результирующего смешанного выходного сигнала. Входные сигналы и результирующий выход смесителя показаны на следующих рисунках.
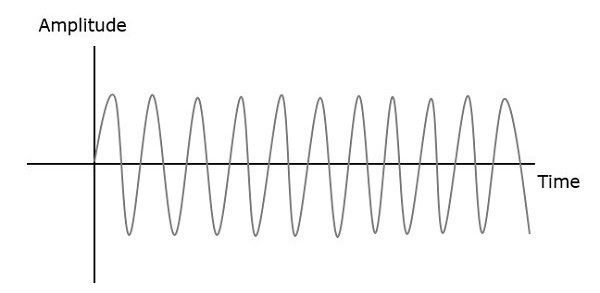

Пусть первая и вторая частоты сигнала равны $ f_1 $ и $ f_2 $. Если эти два сигнала используются в качестве входов РЧ-смесителя, то он создает выходной сигнал с частотами $ f_1 + f_2 $ и $ f_1-f_2 $.
Если это наблюдается в частотной области, картина выглядит как на следующем рисунке.

В этом случае $ f_1 $ больше, чем $ f_2 $. Итак, результирующий результат имеет частоты $ f_1 + f_2 $ и $ f_1-f_2 $. Аналогично, если $ f_2 $ больше, чем $ f_1 $, то результирующий результат будет иметь частоты $ f_1 + f_2 $ и $ f_1-f_2 $.
AM-приемник
Супергетеродинный AM-приемник принимает на входе амплитудно-модулированную волну и выдает исходный аудиосигнал на выходе. Selectivity это способность выбирать один сигнал и отвергать другие. Sensitivity - способность обнаруживать РЧ-сигнал и демодулировать его при самом низком уровне мощности.
Радиолюбители - первые радиоприемники. Однако у них есть такие недостатки, как низкая чувствительность и селективность. Чтобы преодолеть эти недостатки,super heterodyneбыл изобретен ресивер. Блок-схема AM-приемника показана на следующем рисунке.

Радиочастотный тюнер
Амплитудно-модулированная волна, принимаемая антенной, сначала проходит на tuner circuitчерез трансформатор. Схема тюнера - это не что иное, как LC-схема, которую также называютresonant или же tank circuit. Он выбирает частоту, желаемую AM-приемником. Он также одновременно настраивает гетеродин и ВЧ-фильтр.
RF микшер
Сигнал с выхода тюнера отправляется на RF-IF converter, который действует как микшер. Он имеет гетеродин, который производит постоянную частоту. Здесь выполняется процесс микширования, при этом принятый сигнал является одним входом, а частота гетеродина - другим входом. Результирующий выходной сигнал представляет собой смесь двух частот $ \ left [\ left (f_1 + f_2 \ right), \ left (f_1-f_2 \ right) \ right] $, создаваемых микшером, который называетсяIntermediate Frequency (IF).
Формирование IF помогает в демодуляции любого сигнала станции, имеющего любую несущую частоту. Следовательно, все сигналы переводятся на фиксированную несущую частоту для адекватной избирательности.
IF фильтр
Промежуточный частотный фильтр - это полосовой фильтр, пропускающий нужную частоту. Он устраняет все другие нежелательные частотные компоненты, присутствующие в нем. Это преимущество фильтра ПЧ, который допускает только частоту ПЧ.
AM демодулятор
Полученная AM-волна теперь демодулируется с помощью AM-демодулятора. Этот демодулятор использует процесс обнаружения огибающей для приема модулирующего сигнала.
Усилитель звука
Это каскад усилителя мощности, который используется для усиления обнаруженного аудиосигнала. Обработанный сигнал усиливается, чтобы быть эффективным. Этот сигнал передается на громкоговоритель, чтобы получить исходный звуковой сигнал.
FM-приемник
Блок-схема FM-приемника показана на следующем рисунке.

Эта блок-схема FM-приемника аналогична блок-схеме AM-приемника. Два блока Amplitude limiter и De-Accord network включены до и после FM-демодулятора. Работа остальных блоков такая же, как и у AM-приемника.
Мы знаем, что при FM-модуляции амплитуда FM-волны остается постоянной. Однако, если в канал добавлен некоторый шум с FM-волной, из-за этого амплитуда FM-волны может измениться. Таким образом, с помощьюamplitude limiter мы можем поддерживать амплитуду FM-волны постоянной, удаляя нежелательные пики шумового сигнала.
В FM-передатчике мы видели сеть предыскажений (фильтр верхних частот), которая присутствует перед FM-модулятором. Это используется для улучшения отношения сигнал / шум высокочастотного аудиосигнала. Обратный процесс предыскажения известен какde-emphasis. Таким образом, в этом FM-приемнике после FM-демодулятора включена сеть устранения акцентов (фильтр нижних частот). Этот сигнал передается на аудиоусилитель для увеличения уровня мощности. В итоге получаем исходный звуковой сигнал из динамика.
До сих пор мы обсуждали непрерывную модуляцию. Мы обсудим импульсную модуляцию в следующей главе. Эти методы импульсной модуляции работают с дискретными сигналами. Итак, теперь давайте посмотрим, как преобразовать непрерывный сигнал времени в дискретный.
Процесс преобразования сигналов непрерывного времени в эквивалентные сигналы дискретного времени можно обозначить как Sampling. В процессе выборки непрерывно производится выборка данных в определенный момент.
На следующем рисунке показан непрерывный сигнал. x(t) и соответствующий дискретизированный сигнал xs(t). когдаx(t) умножается на периодическую последовательность импульсов, дискретизированный сигнал xs(t) получается.

А sampling signal представляет собой периодическую серию импульсов единичной амплитуды, дискретизируемую через равные промежутки времени $ T_s $, которая называется sampling time. Эти данные передаются в моменты времени $ T_s $, а сигнал несущей передается в оставшееся время.
Частота выборки
Для дискретизации сигналов необходимо устранить разрыв между отсчетами. Этот промежуток можно назвать периодом выборки $ T_s $. Взаимность периода выборки известна какsampling frequency или же sampling rate $f_s$.
Математически мы можем записать это как
$$ f_s = \ frac {1} {T_s} $$
Где,
$ f_s $ - частота дискретизации или частота дискретизации
$ T_s $ - период выборки
Теорема выборки
Частота дискретизации должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Вsampling theorem заявляет, что «сигнал может быть точно воспроизведен, если он дискретизируется со скоростью $ f_s $, которая больше или равна удвоенной максимальной частоте данного сигнала. W. »
Математически мы можем записать это как
$$ f_s \ geq 2W $$
Где,
$ f_s $ - частота дискретизации
$ W $ - самая высокая частота данного сигнала
Если частота дискретизации равна удвоенной максимальной частоте данного сигнала W, то она называется Nyquist rate.
Теорема выборки, которую также называют Nyquist theorem, предоставляет теорию достаточной частоты дискретизации с точки зрения полосы пропускания для класса функций с ограниченной полосой пропускания.
Для сигнала непрерывного времени x(t), которая ограничена полосой частот в частотной области, представлена, как показано на следующем рисунке.

Если частота дискретизации сигнала превышает частоту Найквиста, то исходный сигнал может быть восстановлен. На следующем рисунке поясняется сигнал, если частота дискретизации выше, чем у2w в частотной области.
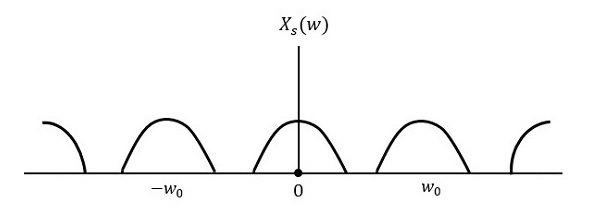
Если тот же сигнал дискретизируется с частотой менее 2w, то дискретизированный сигнал будет выглядеть, как на следующем рисунке.

Из приведенного выше рисунка видно, что информация перекрывается, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называетсяAliasing.
Наложение наложения можно назвать «явлением высокочастотной составляющей в спектре сигнала, которая приобретает идентичность низкочастотной составляющей в спектре его дискретизированной версии».
Следовательно, частота дискретизации сигнала выбирается равной частоте Найквиста. Если частота дискретизации равна удвоенной максимальной частоте данного сигналаW, то дискретизированный сигнал будет выглядеть, как на следующем рисунке.

В этом случае сигнал можно восстановить без потерь. Следовательно, это хорошая частота дискретизации.
После непрерывной волновой модуляции следующим разделом является импульсная модуляция. В этой главе давайте обсудим следующие методы аналоговой импульсной модуляции.
- Амплитудно-импульсная модуляция
- Широтно-импульсная модуляция
- Позиционная импульсная модуляция
Амплитудно-импульсная модуляция
В Pulse Amplitude Modulation (PAM) В этом методе амплитуда несущей импульса изменяется пропорционально мгновенной амплитуде сигнала сообщения.
Сигнал, модулированный по амплитуде импульса, будет следовать за амплитудой исходного сигнала, так как сигнал следует по пути всей волны. В естественном PAM сигнал, отобранный со скоростью Найквиста, может быть восстановлен, пропуская его через эффективныйLow Pass Filter (LPF) с точной частотой среза.
Следующие рисунки поясняют амплитудно-импульсную модуляцию.



Хотя сигнал PAM проходит через фильтр LPF, он не может восстановить сигнал без искажений. Следовательно, чтобы избежать этого шума, используйте выборку с плоской вершиной. Сигнал PAM с плоской крышкой показан на следующем рисунке.

Flat-top sampling- это процесс, в котором дискретизированный сигнал может быть представлен в импульсах, для которых амплитуда сигнала не может быть изменена по сравнению с аналоговым сигналом, подлежащим дискретизации. Вершины амплитуды остаются плоскими. Этот процесс упрощает схемотехнику.
Широтно-импульсная модуляция
В Pulse Width Modulation (PWM) или метод модуляции длительности импульса (PDM) или модуляции времени импульса (PTM), ширина, длительность или время несущей импульса варьируются, что пропорционально мгновенной амплитуде сигнала сообщения.
В этом методе ширина импульса варьируется, но амплитуда сигнала остается постоянной. Ограничители амплитуды используются для обеспечения постоянной амплитуды сигнала. Эти схемы ограничивают амплитуду до желаемого уровня и, следовательно, ограничивают шум.
На следующем рисунке поясняются типы широтно-импульсной модуляции.
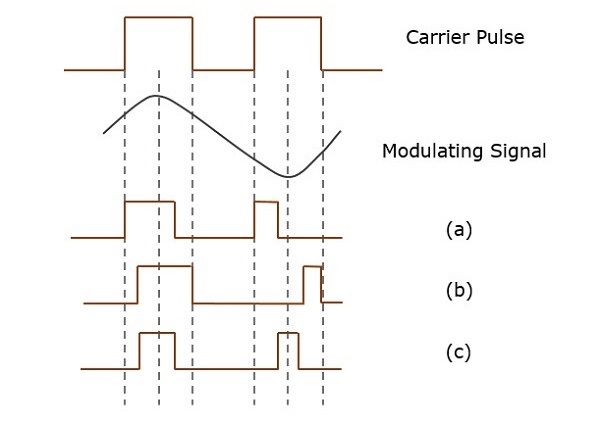
Есть три типа ШИМ.
Передний фронт импульса постоянен, задний фронт изменяется в соответствии с сигналом сообщения. Форма сигнала для этого типа ШИМ обозначена как (a) на рисунке выше.
Поскольку задний фронт импульса постоянен, передний фронт изменяется в соответствии с сигналом сообщения. Форма сигнала для этого типа ШИМ обозначена как (b) на рисунке выше.
Центр импульса постоянен, передний и задний фронт изменяются в соответствии с сигналом сообщения. Форма сигнала для этого типа ШИМ обозначена как (c), показанная на рисунке выше.
Позиционная импульсная модуляция
Pulse Position Modulation (PPM) является аналогом схема модуляции, в которой амплитуда и ширина импульсов поддерживаются постоянная, в то время как положение каждого импульса, со ссылкой на позицию опорного импульса изменяется в зависимости от мгновенного дискретизированного значения сигнала сообщения.
Передатчик должен посылать синхронизирующие импульсы (или просто синхронизирующие импульсы), чтобы поддерживать синхронизацию передатчика и приемника. Эти синхроимпульсы помогают поддерживать положение импульсов. На следующих рисунках поясняется импульсная позиционная модуляция.



Позиционная импульсная модуляция выполняется в соответствии с сигналом с широтно-импульсной модуляцией. Каждый задний фронт сигнала с широтно-импульсной модуляцией становится отправной точкой для импульсов в сигнале PPM. Следовательно, положение этих импульсов пропорционально ширине импульсов ШИМ.
Преимущество
Поскольку амплитуда и ширина постоянны, обрабатываемая мощность также постоянна.
Недостаток
Необходима синхронизация между передатчиком и приемником.
Сравнение PAM, PWM и PPM
В следующей таблице представлено сравнение трех методов модуляции.
| PAM | ШИМ | PPM |
|---|---|---|
| Амплитуда варьируется | Ширина варьируется | Позиция варьируется |
| Полоса пропускания зависит от ширины импульса | Полоса пропускания зависит от времени нарастания импульса | Полоса пропускания зависит от времени нарастания импульса |
| Мгновенная мощность передатчика зависит от амплитуды импульсов. | Мгновенная мощность передатчика зависит от амплитуды и ширины импульсов. | Мгновенная мощность передатчика остается постоянной в зависимости от ширины импульсов. |
| Сложность системы высокая | Сложность системы низкая | Сложность системы низкая |
| Шумовые помехи высокие | Шумовые помехи низкие | Шумовые помехи низкие |
| Это похоже на амплитудную модуляцию | Это похоже на частотную модуляцию | Это похоже на фазовую модуляцию |
Transducerэто устройство, которое преобразует энергию из одной формы в другую. В этой главе давайте обсудим преобразователи, используемые в системах связи.
Зачем нужны преобразователи?
В реальном мире общение между любыми двумя соседними людьми происходит с помощью звуковых волн. Но если люди находятся далеко, то трудно передать информацию без потерь, используя звуковые волны в их физической форме.
Чтобы преодолеть эту трудность, мы можем использовать модуляторы в секции передатчика и демодуляторы в секции приемника. Эти модуляторы и демодуляторы работают с электрическими сигналами. Вот почему нам требуется устройство, которое должно преобразовывать звуковые волны в электрические сигналы или наоборот. Это устройство известно как преобразователь.
Ниже представлена простая блок-схема преобразователя.

Этот преобразователь имеет один вход и один выход. Он преобразует энергию, присутствующую на входе, в эквивалентный выход, имеющий другую энергию. По сути, преобразователь преобразует неэлектрическую форму энергии в электрическую или наоборот.
Типы преобразователей
Мы можем классифицировать преобразователи на следующие two types исходя из размещения (положения) преобразователя в системах связи.
- Входной преобразователь
- Выходной преобразователь
Входные преобразователи
Датчик, присутствующий на входе системы связи, известен как input transducer. Ниже представлена блок-схема входного преобразователя.

Этот входной преобразователь преобразует неэлектрическую физическую величину в электрический сигнал. С помощью этого преобразователя физические величины, такие как звук или свет, могут быть преобразованы в электрические величины, такие как напряжение или ток.Example: Микрофон.
Микрофон используется как входной преобразователь, который размещается между источником информации и передатчиком. Источник информации производит информацию в виде звуковых волн. Вmicrophoneпреобразует эти звуковые волны в электрические сигналы с помощью диафрагмы. Эти электрические сигналы можно использовать для дальнейшей обработки.
Выходные преобразователи
Преобразователь, присутствующий на выходе системы связи, известен как выходной преобразователь. Ниже приведена блок-схемаoutput transducer.

Этот выходной преобразователь преобразует электрический сигнал в неэлектрическую физическую величину. С помощью этого преобразователя электрические величины, такие как напряжение или ток, могут быть преобразованы в физические величины, такие как звук или свет.Example: Громкоговоритель.
Громкоговоритель используется в качестве выходного преобразователя, который помещается между секцией приемника и местом назначения. Демодулятор, присутствующий в секции приемника, выдает демодулированный выходной сигнал. Так чтоloud speakerпреобразует электрические сигналы (демодулированный выходной сигнал) в звуковые волны. Поэтому функциональность громкоговорителя прямо противоположна функциональности микрофона.
В дополнение к указанным выше датчикам, в системах связи используется еще один датчик. Этот преобразователь может быть размещен либо в конце секции передатчика, либо в начале секции приемника.Example: Антенна.
Антенна - это преобразователь, который преобразует электрические сигналы в электромагнитные волны и наоборот. Антенна может использоваться какtransmitting antenna или как receiving antenna.
Передающая антенна преобразует электрические сигналы в электромагнитные волны и излучает их. При этом приемная антенна преобразует электромагнитные волны из принятого луча в электрические сигналы.
В этой двусторонней связи одна и та же антенна может использоваться как для передачи, так и для приема.