Аналоговая связь - FM-модуляторы
В этой главе давайте обсудим модуляторы, которые генерируют волны NBFM и WBFM. Во-первых, давайте обсудим генерацию NBFM.
Генерация NBFM
Мы знаем, что стандартное уравнение FM-волны имеет вид
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) - $
$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $
Для NBFM,
$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$
Мы знаем, что $ \ cos \ theta \ приблизительно 1 $ и $ \ sin \ theta \ приблизительно 1 $, когда $ \ theta $ очень мало.
Используя указанные выше отношения, мы получим NBFM equation в качестве
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ справа) dt $$
Блок-схема модулятора NBFM показана на следующем рисунке.
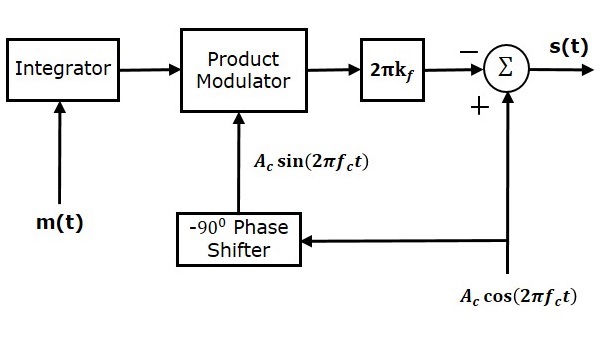
Здесь интегратор используется для интегрирования модулирующего сигнала $ m \ left (t \ right) $. Несущий сигнал $ A_c \ cos \ left (2 \ pi f_ct \ right) $ представляет собой фазу, сдвинутую на $ -90 ^ 0 $, чтобы получить $ A_c \ sin \ left (2 \ pi f_ct \ right) $ с помощью $ -90 ^ 0 $ фазовращатель. Модулятор произведения имеет два входа $ \ int m \ left (t \ right) dt $ и $ A_c \ sin \ left (2 \ pi f_ct \ right) $. Он производит результат, который является продуктом этих двух входов.
Далее это умножается на $ 2 \ pi k_f $, помещая блок $ 2 \ pi k_f $ в прямой путь. Летний блок имеет два входа, которые представляют собой не что иное, как два члена уравнения NBFM. Положительный и отрицательный знаки присваиваются несущему сигналу и другому члену на входе летнего блока. Наконец, летний блок дает волну NBFM.
Генерация WBFM
Следующие два метода генерируют волну WBFM.
- Прямой метод
- Косвенный метод
Прямой метод
Этот метод называется прямым методом, потому что мы напрямую генерируем широкополосную FM-волну. В этом методе для генерации WBFM используется генератор, управляемый напряжением (VCO). ГУН выдает выходной сигнал, частота которого пропорциональна напряжению входного сигнала. Это похоже на определение FM-волны. Блок-схема генерации волны WBFM показана на следующем рисунке.

Здесь модулирующий сигнал $ m \ left (t \ right) $ подается на вход генератора, управляемого напряжением (ГУН). VCO производит выходной сигнал, который представляет собой не что иное, как WBFM.
$$ f_i \: \ alpha \: m \ left (t \ right) $$
$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $$
Куда,
$ f_i $ - мгновенная частота волны WBFM.
Косвенный метод
Этот метод называется косвенным, потому что мы косвенно генерируем широкополосную FM-волну. Это означает, что сначала мы сгенерируем волну NBFM, а затем с помощью умножителей частоты получим волну WBFM. Блок-схема генерации WBFM-волны показана на следующем рисунке.

Эта блок-схема состоит в основном из двух этапов. На первом этапе волна NBFM будет сгенерирована с помощью модулятора NBFM. Мы видели блок-схему модулятора NBFM в начале этой главы. Мы знаем, что индекс модуляции волны NBFM меньше единицы. Следовательно, чтобы получить требуемый индекс модуляции (больше единицы) FM-волны, правильно выберите значение множителя частоты.
Frequency multiplierпредставляет собой нелинейное устройство, которое производит выходной сигнал, частота которого в n раз превышает частоту входного сигнала. Где n - коэффициент умножения.
Если волна NBFM, индекс модуляции которой $ \ beta $ меньше 1, применяется в качестве входа умножителя частоты, то умножитель частоты формирует выходной сигнал, индекс модуляции которого равен n умножить на $ \ beta $, а частота также n 'умноженная на частоту волны WBFM.
Иногда нам может потребоваться несколько ступеней умножителя частоты и смесителей, чтобы увеличить девиацию частоты и индекс модуляции FM-волны.