Аналоговая связь - модуляция VSBSC
В предыдущих главах мы обсуждали модуляцию SSBSC и демодуляцию. Модулированный сигнал SSBSC имеет только одну частоту боковой полосы. Теоретически мы можем полностью получить одну частотную составляющую боковой полосы, используя идеальный полосовой фильтр. Однако практически мы не можем получить всю частотную составляющую боковой полосы. Из-за этого теряется некоторая информация.
Чтобы избежать этой потери, выбран метод, являющийся компромиссом между DSBSC и SSBSC. Этот метод известен какVestigial Side Band Suppressed Carrier (VSBSC)техника. Слово «остаток» означает «часть», от которой и произошло название.
VSBSC Modulationэто процесс, в котором часть сигнала, называемая следом, модулируется вместе с одной боковой полосой. Частотный спектр волны VSBSC показан на следующем рисунке.

Наряду с верхней боковой полосой, в этом методе передается также часть нижней боковой полосы. Точно так же мы можем передавать нижнюю боковую полосу вместе с частью верхней боковой полосы. Защитная полоса очень маленькой ширины проложена по обе стороны от VSB, чтобы избежать помех. Модуляция VSB в основном используется в телевизионных передачах.
Полоса пропускания модуляции VSBSC
Мы знаем, что ширина полосы модулированной волны SSBSC равна $ f_m $. Поскольку модулированная волна VSBSC содержит частотные компоненты одной боковой полосы вместе с остатком другой боковой полосы, ее ширина будет суммой ширины полосы модулированной волны SSBSC и остаточной частоты $ f_v $.
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
Преимущества
Ниже приведены преимущества модуляции VSBSC.
Высокоэффективный.
Уменьшение полосы пропускания по сравнению с волнами AM и DSBSC.
Конструкция фильтра проста, поскольку не требуется высокой точности.
Передача низкочастотных компонентов возможна без каких-либо затруднений.
Обладает хорошими фазовыми характеристиками.
Недостатки
Ниже приведены недостатки модуляции VSBSC.
Пропускная способность больше по сравнению с волной SSBSC.
Демодуляция сложна.
Приложения
Наиболее известное и стандартное применение VSBSC - это передача телевизионных сигналов. Кроме того, это наиболее удобный и эффективный метод с учетом использования полосы пропускания.
Теперь давайте обсудим модулятор, который генерирует волны VSBSC, и демодулятор, который демодулирует волны VSBSC один за другим.
Генерация VSBSC
Генерация волны VSBSC аналогична генерации волны SSBSC. Модулятор VSBSC показан на следующем рисунке.
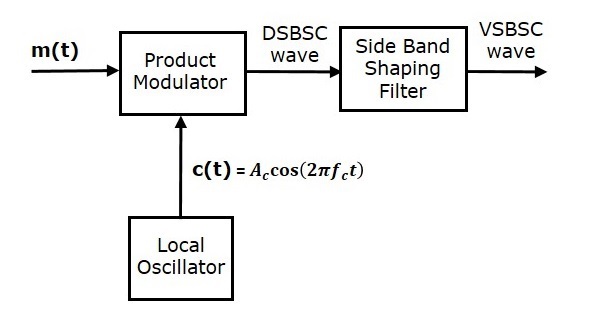
В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входа для фильтра формирования боковой полосы. Этот фильтр производит выходной сигнал, представляющий собой волну VSBSC.
Модулирующий сигнал $ m \ left (t \ right) $ и сигнал несущей $ A_c \ cos \ left (2 \ pi f_ct \ right) $ используются в качестве входных сигналов для модулятора произведения. Следовательно, модулятор продукта выдает выходной сигнал, который является произведением этих двух входов.
Следовательно, выходной сигнал модулятора продукта равен
$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
Примените преобразование Фурье с обеих сторон
$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$
Вышеприведенное уравнение представляет собой уравнение частотного спектра DSBSC.
Пусть передаточная функция фильтра формирования боковой полосы равна $ H \ left (f \ right) $. Этот фильтр имеет вход $ p \ left (t \ right) $, а выход - модулированную VSBSC волну $ s \ left (t \ right) $. Преобразования Фурье $ p \ left (t \ right) $ и $ s \ left (t \ right) $ равны $ P \ left (t \ right) $ и $ S \ left (t \ right) $ соответственно.
Математически мы можем записать $ S \ left (f \ right) $ как
$$ S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right) $$
Подставьте значение $ P \ left (f \ right) $ в приведенное выше уравнение.
$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right) $$
Вышеприведенное уравнение представляет собой уравнение частотного спектра VSBSC.
Демодуляция VSBSC
Демодуляция волны VSBSC аналогична демодуляции волны SSBSC. Здесь тот же несущий сигнал (который используется для генерации волны VSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называетсяcoherent или synchronous detection. Демодулятор VSBSC показан на следующем рисунке.

В этом процессе сигнал сообщения может быть извлечен из волны VSBSC путем умножения его на несущую, которая имеет ту же частоту и фазу несущей, которые используются в модуляции VSBSC. Результирующий сигнал затем проходит через фильтр нижних частот. Выход этого фильтра - сигнал желаемого сообщения.
Пусть волна VSBSC будет $ s \ left (t \ right) $, а сигнал несущей - $ A_c \ cos \ left (2 \ pi f_ct \ right) $.
На рисунке мы можем записать выходной сигнал модулятора продукта как
$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$
Примените преобразование Фурье с обеих сторон
$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$
Мы знаем, что $ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ влево (f \ right) $
Из приведенного выше уравнения найдем $ S \ left (f-f_c \ right) $ и $ S \ left (f + f_c \ right) $.
$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ right] H \ left (f-f_c \ right) $$
$ \ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right) $
$$ S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ right] H \ left (f + f_c \ right) $$
$ \ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right) $
Замените значения $ S \ left (f-f_c \ right) $ и $ S \ left (f + f_c \ right) $ в $ V \ left (f \ right) $.
$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $
$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $
$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ влево (f + f_c \ right) \ right] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ right) H \ left (f + f_c \ right) \ right] $
В приведенном выше уравнении первый член представляет масштабированную версию частотного спектра сигнала полезного сообщения. Его можно извлечь, пропустив указанный выше сигнал через фильтр нижних частот.
$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right] $$