Дискретная математика - теория групп

Полугруппа

Конечное или бесконечное множество $ 'S' $ с бинарной операцией $ '\ omicron' $ (композиция) называется полугруппой, если оно выполняется одновременно при следующих двух условиях:

Closure - Для каждой пары $ (a, b) \ in S, \ :( a \ omicron b) $ должна присутствовать в множестве $ S $.
Associative - Для каждого элемента $ a, b, c \ в S должно выполняться (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $.

пример

Множество натуральных чисел (кроме нуля) с операцией сложения является полугруппой. Например, $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $

Здесь свойство замыкания выполняется, так как для каждой пары $ (a, b) \ in S, (a + b) $ присутствует в множестве S. Например, $ 1 + 2 = 3 \ in S] $

Свойство ассоциации также имеет место для каждого элемента $ a, b, c \ в S, (a + b) + c = a + (b + c) $. Например, $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $.

Моноид

Моноид - это полугруппа с единичным элементом. Единичный элемент (обозначаемый $ e $ или E) множества S - это такой элемент, что $ (a \ omicron e) = a $ для каждого элемента $ a \ in S $. Элемент идентичности также называетсяunit element. Итак, моноид одновременно обладает тремя свойствами -Closure, Associative, Identity element.

пример

Множество натуральных чисел (кроме нуля) с операцией умножения является моноидом. $ S = \ lbrace 1, 2, 3, \ точки \ rbrace $

Здесь свойство замыкания выполняется, так как для каждой пары $ (a, b) \ in S, (a \ times b) $ присутствует в множестве S. [Например, $ 1 \ times 2 = 2 \ in S $ и т. Д.]

Ассоциативное свойство также выполняется для каждого элемента $ a, b, c \ в S, (a \ times b) \ times c = a \ times (b \ times c) $ [Например, $ (1 \ times 2) \ times 3 = 1 \ times (2 \ times 3) = 6 $ и так далее]

Свойство идентичности также выполняется для каждого элемента $ a \ in S, (a \ times e) = a $ [Например, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ и так далее]. Здесь элемент идентичности равен 1.

Группа

Группа - это моноид с обратным элементом. Обратный элемент (обозначенный I) множества S - это такой элемент, что $ (a \ omicron I) = (I \ omicron a) = a $ для каждого элемента $ a \ in S $. Итак, группа обладает четырьмя свойствами одновременно: i) замкнутость, ii) ассоциативность, iii) элемент идентичности, iv) обратный элемент. Порядок группы G - это количество элементов в G, а порядок элемента в группе - это наименьшее положительное целое число n такое, что an является единичным элементом этой группы G.

Примеры

Множество $ N \ times N $ невырожденных матриц образуют группу при операции матричного умножения.

Произведение двух $ N \ times N $ невырожденных матриц также является невырожденной матрицей $ N \ times N $, обладающей свойством замыкания.

Само умножение матриц ассоциативно. Следовательно, ассоциативность сохраняется.

Набор из $ N \ times N $ невырожденных матриц содержит единичную матрицу, обладающую свойством единичного элемента.

Поскольку все матрицы неособые, все они имеют обратные элементы, которые также являются невырожденными матрицами. Следовательно, имеет место и обратное свойство.

Абелева группа

Абелева группа G - это группа, для которой пара элементов $ (a, b) \ in G $ всегда имеет коммутативный закон. Итак, группа обладает пятью свойствами одновременно: i) замкнутость, ii) ассоциативность, iii) элемент идентичности, iv) обратный элемент, v) коммутативный.

пример

Множество натуральных чисел (включая ноль) с операцией сложения является абелевой группой. $ G = \ lbrace 0, 1, 2, 3, \ точки \ rbrace $

Здесь свойство замыкания выполняется, поскольку для каждой пары $ (a, b) \ in S, (a + b) $ присутствует в множестве S. [Например, $ 1 + 2 = 2 \ in S $ и так далее]

Ассоциативное свойство также выполняется для каждого элемента $ a, b, c \ в S, (a + b) + c = a + (b + c) $ [Например, $ (1 +2) + 3 = 1 + (2 + 3) = 6 $ и так далее]

Коммутативность также сохраняется для каждого элемента $ a \ in S, (a \ times b) = (b \ times a) $ [Например, $ (2 \ times 3) = (3 \ times 2) = 3 $ и поэтому на]

Циклическая группа и подгруппа

А cyclic groupэто группа, которая может быть создана одним элементом. Каждый элемент циклической группы - это мощность определенного элемента, который называется генератором. Циклическая группа может быть сгенерирована генератором «g», так что любой другой элемент группы может быть записан как мощность генератора «g».

пример

Множество комплексных чисел $ \ lbrace 1, -1, i, -i \ rbrace $ при операции умножения является циклической группой.

Есть два генератора - $ i $ и $ –i $ как $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $, а также $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $, который охватывает все элементы группы. Следовательно, это циклическая группа.

Note - А cyclic groupвсегда является абелевой группой, но не всякая абелева группа является циклической группой. Добавляемые рациональные числа не циклические, а абелевы.

А subgroup H является подмножеством группы G (обозначается $ H ≤ G $), если оно одновременно удовлетворяет четырем свойствам: Closure, Associative, Identity element, и Inverse.

Подгруппа H группы G, которая не включает всю группу G, называется собственной подгруппой (обозначается $ H <G $). Подгруппа циклической группы циклическая, и абелева подгруппа также абелева.

пример

Пусть группа $ G = \ lbrace 1, i, -1, -i \ rbrace $

Тогда некоторые подгруппы - это $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,

Это не подгруппа - $ H_3 = \ lbrace 1, i \ rbrace $, потому что $ (i) ^ {- 1} = -i $ не входит в $ H_3 $

Частично заказанный набор (POSET)

Частично упорядоченный набор состоит из набора с бинарным отношением, которое является рефлексивным, антисимметричным и транзитивным. «Частично упорядоченный набор» сокращенно называется POSET.

Примеры

Множество действительных чисел при бинарной операции, меньшее или равное $ (\ le) $, является ч.у.

Пусть набор $ S = \ lbrace 1, 2, 3 \ rbrace $ и операция $ \ le $

Отношения будут такими: $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $

Это отношение R рефлексивно как $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $

Это отношение R антисимметрично, так как

$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ и \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ Реалов

Это отношение R также транзитивно как $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ in R $.

Следовательно, это poset.
Множество вершин ориентированного ациклического графа при выполнении операции «достижимость» является ч.у.

Диаграмма Хассе

Диаграмма Хассе чугуна - это ориентированный граф, вершины которого являются элементами чугуна, а дуги покрывают пары (x, y) в чум. Если в poset $ x <y $, то точка x оказывается ниже точки y на диаграмме Хассе. Если $ x <y <z $ в poset, то стрелка не отображается между x и z, поскольку это неявно.

пример

Набор подмножеств $ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ показано на следующей диаграмме Хассе -

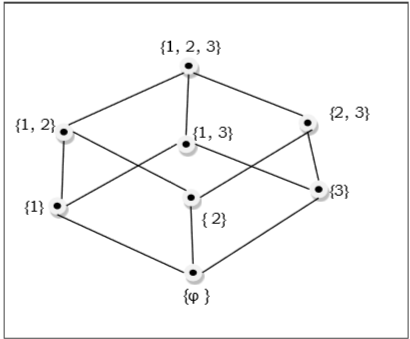
Линейно упорядоченный набор

Линейно упорядоченный набор или Полный упорядоченный набор - это набор частичного порядка, в котором каждая пара элементов сопоставима. Элементы $ a, b \ in S $ называются сравнимыми, если выполняется либо $ a \ le b $, либо $ b \ le a $. Закон трихотомии определяет этот полный упорядоченный набор. Полностью упорядоченный набор можно определить как распределительную решетку, обладающую свойством $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ для всех значений a и b в наборе S.

пример

Набор мощности $ \ lbrace a, b \ rbrace $, упорядоченный с помощью \ substeq, является полностью упорядоченным набором, как и все элементы набора мощности $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ сопоставимы.

Пример неполного набора заказов

Набор $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ при операции x делит y не является полным упорядоченным набором.

Здесь для всех $ (x, y) \ in S, x | y $ должны выполняться, но это неверно, что 2 | 3, поскольку 2 не делит 3 или 3 не делит 2. Следовательно, это не полный упорядоченный набор.

Решетка

Решетка - это ЧУМ $ (L, \ le) $, для которого каждая пара $ \ lbrace a, b \ rbrace \ in L $ имеет точную верхнюю границу (обозначается $ a \ lor b $) и точную нижнюю грань ( обозначается $ a \ land b $). LUB $ (\ lbrace a, b \ rbrace) $ называется объединением a и b. GLB $ (\ lbrace a, b \ rbrace) $ называется пересечением точек a и b.

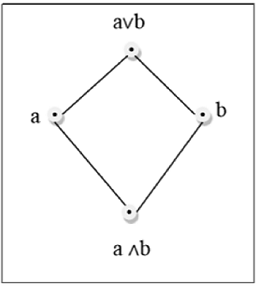
пример

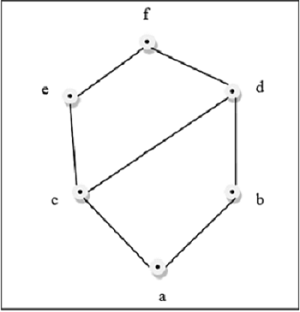
Этот рисунок выше представляет собой решетку, потому что для каждой пары $ \ lbrace a, b \ rbrace \ in L $ существуют GLB и LUB.

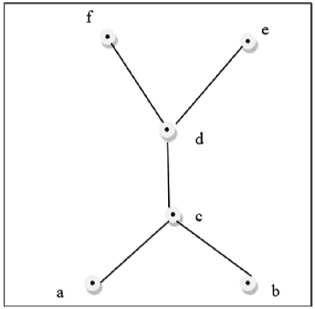
Этот рисунок выше не является решеткой, потому что $ GLB (a, b) $ и $ LUB (e, f) $ не существует.

Некоторые другие решетки обсуждаются ниже -

Ограниченная решетка

Решетка L становится ограниченной решеткой, если у нее есть наибольший элемент 1 и наименьший элемент 0.

Дополненная решетка

Решетка L становится решеткой с дополнениями, если она является ограниченной решеткой и если каждый элемент в решетке имеет дополнение. Элемент x имеет дополнение x ', если $ \ существует x (x \ land x' = 0 и x \ lor x '= 1) $