Дискретная математика - Наборы

Немецкий математик G. Cantorввел понятие множеств. Он определил набор как набор определенных и различимых объектов, выбранных с помощью определенных правил или описания.

SetТеория составляет основу нескольких других областей исследования, таких как теория счета, отношения, теория графов и конечные автоматы. В этой главе мы рассмотрим различные аспектыSet Theory.

Набор - Определение

Набор - это неупорядоченный набор различных элементов. Набор можно записать явно, перечислив его элементы с помощью скобок набора. Если порядок элементов изменяется или любой элемент набора повторяется, он не вносит никаких изменений в набор.

Некоторые примеры наборов

Набор всех положительных целых чисел
Набор всех планет солнечной системы
Набор всех штатов Индии
Набор всех строчных букв алфавита

Представление множества

Наборы могут быть представлены двумя способами -

Реестр или табличная форма
Обозначение конструктора множеств

Реестр или табличная форма

Набор представлен перечислением всех составляющих его элементов. Элементы заключаются в фигурные скобки и разделяются запятыми.

Example 1 - Набор гласных в английском алфавите, $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 - Набор нечетных чисел меньше 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

Обозначение конструктора множеств

Набор определяется путем указания свойства, которое является общим для элементов набора. Набор описывается как $ A = \ lbrace x: p (x) \ rbrace $

Example 1 - Множество $ \ lbrace a, e, i, o, u \ rbrace $ записывается как -

$ A = \ lbrace x: \ text {x - гласная в английском алфавите} \ rbrace $

Example 2 - Набор $ \ lbrace 1,3,5,7,9 \ rbrace $ записывается как -

$ B = \ lbrace x: 1 \ le x \ lt 10 \ и \ (x \% 2) \ ne 0 \ rbrace $

Если элемент x является членом любого множества S, он обозначается $ x \ in S $, а если элемент y не является членом множества S, он обозначается $ y \ notin S $.

Example- Если $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $, но $ 1.5 \ notin S $

Некоторые важные наборы

N - множество всех натуральных чисел = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z - набор всех целых чисел = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ - множество всех положительных целых чисел

Q - множество всех рациональных чисел

R - набор всех действительных чисел

W - набор всех целых чисел

Мощность множества

Мощность множества S, обозначаемая $ | S | $, - это количество элементов множества. Число также называют кардинальным числом. Если набор содержит бесконечное число элементов, его мощность равна $ \ infty $.

Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $

Если есть два набора X и Y,

$ | X | = | Y | $ обозначает два множества X и Y, имеющих одинаковую мощность. Это происходит, когда количество элементов в X в точности равно количеству элементов в Y. В этом случае существует биективная функция f от X до Y.
$ | X | \ le | Y | $ означает, что мощность множества X меньше или равна мощности множества Y. Это происходит, когда количество элементов в X меньше или равно количеству Y. Здесь существует инъективная функция 'f' от X до Y.
$ | X | \ lt | Y | $ означает, что мощность множества X меньше мощности множества Y. Это происходит, когда количество элементов в X меньше, чем у Y. Здесь функция 'f' от X до Y является инъективной функцией, но не биективной.
$ Если \ | X | \ le | Y | $ и $ | X | \ ge | Y | $, тогда $ | X | = | Y | $. Наборы X и Y обычно называют эквивалентными наборами.

Типы наборов

Наборы можно разделить на множество типов. Некоторые из них являются конечными, бесконечными, подмножествами, универсальными, собственными, одноэлементными наборами и т. Д.

Конечный набор

Набор, содержащий определенное количество элементов, называется конечным набором.

Example- $ S = \ lbrace x \: | \: x \ in N $ и $ 70 \ gt x \ gt 50 \ rbrace $

Бесконечный набор

Набор, содержащий бесконечное количество элементов, называется бесконечным набором.

Example- $ S = \ lbrace x \: | \: x \ in N $ и $ x \ gt 10 \ rbrace $

Подмножество

Множество X является подмножеством множества Y (записывается как $ X \ substeq Y $), если каждый элемент X является элементом множества Y.

Example 1- Пусть, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ и $ Y = \ lbrace 1, 2 \ rbrace $. Здесь множество Y является подмножеством множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем написать $ Y \ substeq X $.

Example 2- Пусть, $ X = \ lbrace 1, 2, 3 \ rbrace $ и $ Y = \ lbrace 1, 2, 3 \ rbrace $. Здесь множество Y является подмножеством (не собственным подмножеством) множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем написать $ Y \ substeq X $.

Правильное подмножество

Термин «собственное подмножество» можно определить как «подмножество, но не равное». Набор X является собственным подмножеством множества Y (записывается как $ X \ subset Y $), если каждый элемент X является элементом множества Y и $ | X | \ lt | Y | $.

Example- Пусть, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ и $ Y = \ lbrace 1, 2 \ rbrace $. Здесь установите $ Y \ subset X $, поскольку все элементы в $ Y $ также содержатся в $ X $, а в $ X $ есть хотя бы один элемент больше, чем набор $ Y $.

Универсальный набор

Это набор всех элементов в определенном контексте или приложении. Все наборы в этом контексте или приложении по существу являются подмножествами этого универсального набора. Универсальные наборы представлены в виде $ U $.

Example- Мы можем определить $ U $ как совокупность всех животных на Земле. В этом случае множество всех млекопитающих является подмножеством $ U $, множество всех рыб - подмножеством $ U $, множество всех насекомых - подмножеством $ U $ и так далее.

Пустой набор или нулевой набор

Пустой набор не содержит элементов. Обозначается он $ \ emptyset $. Поскольку количество элементов в пустом наборе конечно, пустое множество является конечным множеством. Мощность пустого набора или нулевого набора равна нулю.

Example- $ S = \ lbrace x \: | \: x \ in N $ и $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

Одноэлементный набор или набор единиц

Одноэлементный набор или набор единиц содержат только один элемент. Одноэлементный набор обозначается $ \ lbrace s \ rbrace $.

Example- $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

Равный набор

Если два набора содержат одинаковые элементы, они считаются равными.

Example - Если $ A = \ lbrace 1, 2, 6 \ rbrace $ и $ B = \ lbrace 6, 1, 2 \ rbrace $, они равны, поскольку каждый элемент множества A является элементом множества B и каждый элемент множества B - элемент множества A.

Эквивалентный набор

Если мощности двух наборов одинаковы, они называются эквивалентными наборами.

Example- Если $ A = \ lbrace 1, 2, 6 \ rbrace $ и $ B = \ lbrace 16, 17, 22 \ rbrace $, они эквивалентны, поскольку мощность A равна мощности B. т.е. $ | A | = | B | = 3 $

Набор перекрытия

Два набора, у которых есть хотя бы один общий элемент, называются перекрывающимися наборами.

В случае перекрытия наборов -

$ n (A \ чашка B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ чашка B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $

Example- Пусть, $ A = \ lbrace 1, 2, 6 \ rbrace $ и $ B = \ lbrace 6, 12, 42 \ rbrace $. Существует общий элемент «6», следовательно, эти наборы являются перекрывающимися наборами.

Непересекающееся множество

Два множества A и B называются непересекающимися множествами, если у них нет хотя бы одного общего элемента. Следовательно, непересекающиеся множества обладают следующими свойствами:

$ n (A \ cap B) = \ emptyset $
$ n (A \ чашка B) = n (A) + n (B) $

Example - Пусть, $ A = \ lbrace 1, 2, 6 \ rbrace $ и $ B = \ lbrace 7, 9, 14 \ rbrace $, нет ни одного общего элемента, следовательно, эти множества являются перекрывающимися множествами.

Диаграммы Венна

Диаграмма Венна, изобретенная в 1880 году Джоном Венном, представляет собой схематическую диаграмму, которая показывает все возможные логические отношения между различными математическими множествами.

Examples

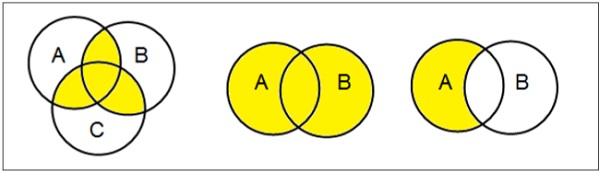
Установить операции

К операциям с множеством относятся: «Установить соединение», «Установить пересечение», «Установить разность», «Дополнение к множеству» и «Декартово произведение».

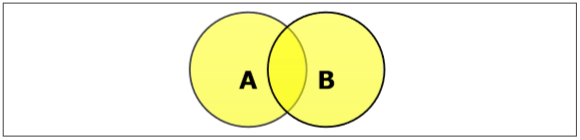
Установить союз

Объединение множеств A и B (обозначается $ A \ cup B $) - это набор элементов, которые находятся в A, в B или в обоих A и B. Следовательно, $ A \ cup B = \ lbrace x \: | \: x \ in A \ OR \ x \ in B \ rbrace $.

Example- Если $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ и B = $ \ lbrace 13, 14, 15 \ rbrace $, то $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (Общий элемент встречается только один раз)

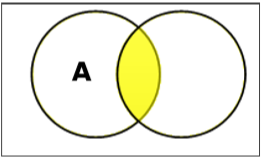
Установить пересечение

Пересечение множеств A и B (обозначается $ A \ cap B $) - это множество элементов, которые находятся как в A, так и в B. Следовательно, $ A \ cap B = \ lbrace x \: | \: x \ in A \ И \ x \ в B \ rbrace $.

Example - Если $ A = \ lbrace 11, 12, 13 \ rbrace $ и $ B = \ lbrace 13, 14, 15 \ rbrace $, то $ A \ cap B = \ lbrace 13 \ rbrace $.

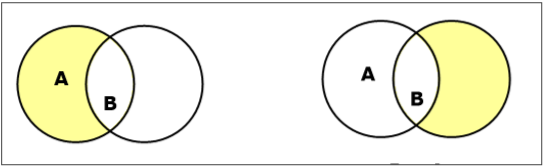
Установить разницу / относительное дополнение

Разность множеств множеств A и B (обозначается $ A - B $) - это множество элементов, которые находятся только в A, но не в B. Следовательно, $ A - B = \ lbrace x \: | \: x \ in A \ AND \ x \ notin B \ rbrace $.

Example- Если $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ и $ B = \ lbrace 13, 14, 15 \ rbrace $, то $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ и $ (B - A) = \ lbrace 14, 15 \ rbrace $. Здесь мы видим $ (A - B) \ ne (B - A) $

Дополнение набора

Дополнением к множеству A (обозначаемым $ A '$) является множество элементов, которых нет в множестве A. Следовательно, $ A' = \ lbrace x | x \ notin A \ rbrace $.

В частности, $ A '= (U - A) $, где $ U $ - универсальный набор, содержащий все объекты.

Example- Если $ A = \ lbrace x \: | \: x \ \: {принадлежит \: к \: множеству \: из \: нечетных \: целых чисел} \ rbrace $, затем $ A '= \ lbrace y \: | \: y \ \: {не \: не \: принадлежит \: к \: множеству \: из \: нечетных \: целых чисел} \ rbrace $

Декартово произведение / перекрестное произведение

Декартово произведение n числа множеств $ A_1, A_2, \ dots A_n $, обозначенных как $ A_1 \ times A_2 \ dots \ times A_n $, можно определить как все возможные упорядоченные пары $ (x_1, x_2, \ dots x_n) $, где $ x_1 \ in A_1, x_2 \ in A_2, \ dots x_n \ in A_n $

Example - Если взять два набора $ A = \ lbrace a, b \ rbrace $ и $ B = \ lbrace 1, 2 \ rbrace $,

Декартово произведение A и B записывается как - $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $

Декартово произведение B и A записывается как - $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

Набор мощности

Набор мощности набора S - это набор всех подмножеств S, включая пустой набор. Мощность набора мощности множества S мощности n равна $ 2 ^ n $. Набор мощности обозначается как $ P (S) $.

Example −

Для набора $ S = \ lbrace a, b, c, d \ rbrace $ вычислим подмножества -

Подмножества с 0 элементами - $ \ lbrace \ emptyset \ rbrace $ (пустой набор)
Подмножества с 1 элементом - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Подмножества с 2 элементами - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Подмножества с 3 элементами - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Подмножества с 4 элементами - $ \ lbrace a, b, c, d \ rbrace $

Следовательно, $ P (S) = $

$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 $

Note - Набор мощности пустого набора также является пустым набором.

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

Разбиение набора

Разбиение набора, скажем, S , - это набор из n непересекающихся подмножеств, скажем $ P_1, P_2, \ dots P_n $, который удовлетворяет следующим трем условиям:

$ P_i $ не содержит пустого множества.

$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
Объединение подмножеств должно равняться всему исходному набору.

$ \ lbrack P_1 \ чашка P_2 \ чашка \ точки \ чашка P_n = S \ rbrack $
Пересечение любых двух различных множеств пусто.

$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \, где \ n \ ge a, \: b \ ge 0 \ rbrack $

Example

Пусть $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

Одно из возможных разбиений - это $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $

Другое возможное разбиение - это $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $