Введение в деревья

Treeпредставляет собой дискретную структуру, которая представляет иерархические отношения между отдельными элементами или узлами. Дерево, в котором родитель имеет не более двух дочерних элементов, называется двоичным деревом.

Дерево и его свойства

Definition- Дерево - это связный ациклический неориентированный граф. Между каждой парой вершин в $ G $ существует единственный путь. Дерево с числом вершин N содержит $ (N-1) $ ребер. Вершина, имеющая нулевую степень, называется корнем дерева. Вершина, имеющая 1 степень, называется листовым узлом дерева, а степень внутреннего узла не менее 2.

Example - Ниже приведен пример дерева -

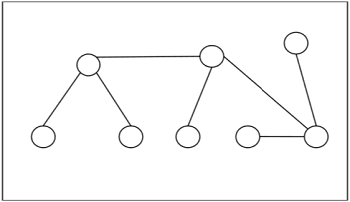
Центры и би-центры дерева

Центр дерева - это вершина с минимальным эксцентриситетом. Эксцентриситет вершины $ X $ в дереве $ G $ - это максимальное расстояние между вершиной $ X $ и любой другой вершиной дерева. Максимальный эксцентриситет - это диаметр дерева. Если дерево имеет только один центр, оно называется центральным деревом, а если дерево имеет только более одного центра, оно называется двухцентровым деревом. Каждое дерево может быть центральным или двухцентровым.

Алгоритм поиска центров и двухцентров дерева

Step 1 - Удалите все вершины степени 1 из данного дерева, а также удалите их инцидентные ребра.

Step 2- Повторяйте шаг 1 до тех пор, пока не останется одна или две вершины, соединенные ребром. Если осталась одна вершина, то это центр дерева, а если две вершины, соединенные ребром, остались, то это би-центр дерева.

Problem 1

Найдите центр / би-центр следующего дерева -

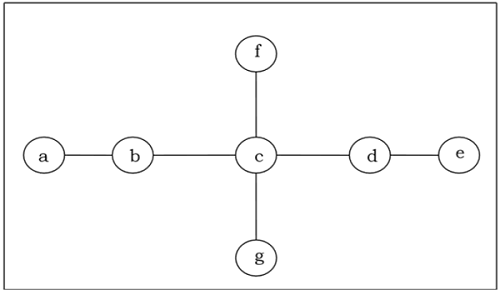
Solution

Сначала мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:

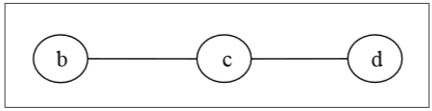
Опять же, мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:

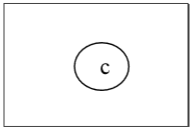
Наконец, у нас есть единственная вершина «c», и мы останавливаем алгоритм. Поскольку существует единственная вершина, это дерево имеет один центр 'c', и дерево является центральным деревом.

Problem 2

Найдите центр / би-центр следующего дерева -

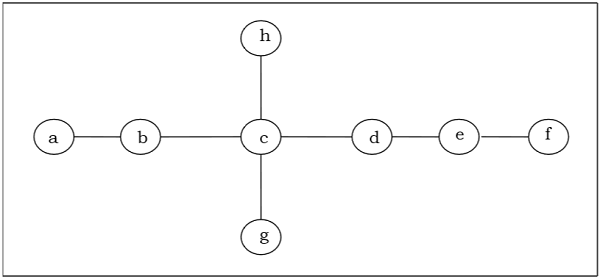
Solution

Сначала мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:

Опять же, мы удалим все вершины степени 1, а также удалим их инцидентные ребра и получим следующее дерево:

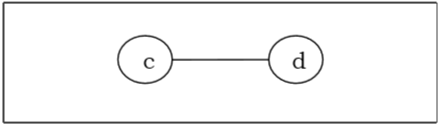
Наконец, у нас остались две вершины «c» и «d», поэтому мы останавливаем алгоритм. Поскольку две вершины, соединенные ребром, остались, это дерево имеет бицентр 'cd' и дерево является бицентральным.

Маркированные деревья

Definition- Размеченное дерево - это дерево, вершинам которого присвоены уникальные номера от 1 до n. Мы можем подсчитать такие деревья для малых значений n вручную, чтобы вывести общую формулу. Количество помеченных деревьев с числом вершин n равно $ n ^ {n-2} $. Два помеченных дерева изоморфны, если их графы изоморфны и соответствующие точки двух деревьев имеют одинаковые метки.

пример

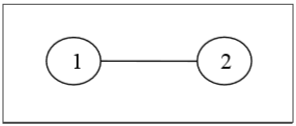
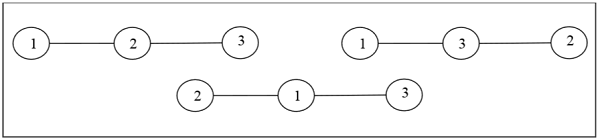
Немаркированные деревья

Definition- Дерево без меток - это дерево, вершинам которого не присвоены номера. Количество помеченных деревьев с числом вершин n равно $ \ frac {(2n)!} {(N + 1)! N! } $ (n- ^е каталонское число)

пример

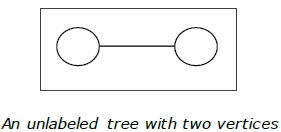
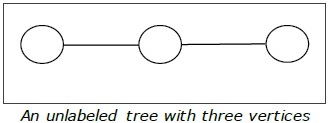
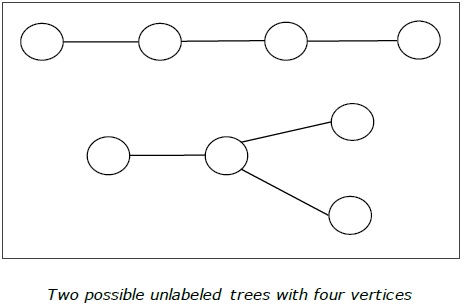
Укоренившееся дерево

Корневое дерево $ G $ - это связный ациклический граф со специальным узлом, который называется корнем дерева, и каждое ребро прямо или косвенно происходит от корня. Упорядоченное корневое дерево - это корневое дерево, в котором упорядочены дочерние элементы каждой внутренней вершины. Если каждая внутренняя вершина корневого дерева имеет не более m дочерних элементов, это называется m-арным деревом. Если каждая внутренняя вершина корневого дерева имеет ровно m детей, это называется полным m-арным деревом. Если $ m = 2 $, корневое дерево называется двоичным деревом.

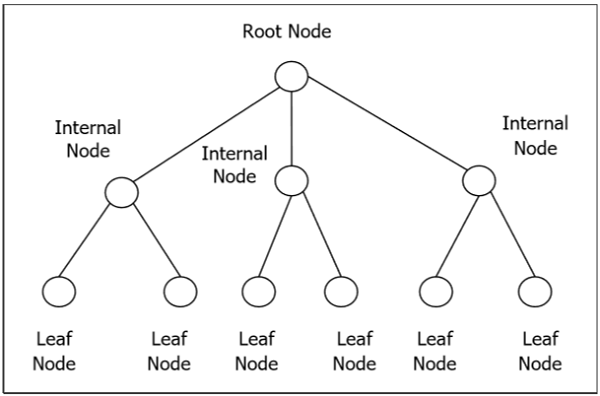
Дерево двоичного поиска

Дерево двоичного поиска - это двоичное дерево, которое удовлетворяет следующему свойству:

• $ X $ в левом поддереве вершины $ V, Value (X) \ le Value (V) $
• $ Y $ в правом поддереве вершины $ V, Value (Y) \ ge Value (V) $

Итак, значение всех вершин левого поддерева внутреннего узла $ V $ меньше или равно $ V $, а значение всех вершин правого поддерева внутреннего узла $ V $ больше или равны $ V $. Количество ссылок от корневого узла к самому глубокому узлу - это высота двоичного дерева поиска.

пример

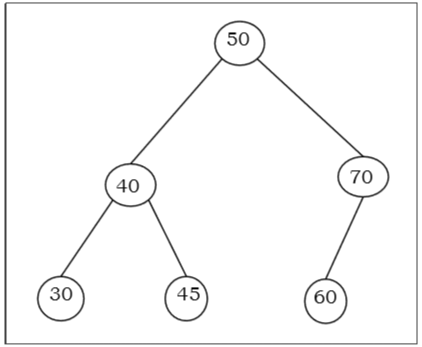
Алгоритм поиска ключа в BST

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)

Сложность двоичного дерева поиска

	Средний случай	Худший случай
Космическая сложность	На)	На)
Сложность поиска	O (журнал n)	На)
Сложность вставки	O (журнал n)	На)
Сложность удаления	O (журнал n)	На)