Дискретная математика - Подробнее о графах
Раскраска графика
Раскраска графа - это процедура присвоения цвета каждой вершине графа G таким образом, чтобы никакие соседние вершины не были одного цвета. Цель - минимизировать количество цветов при раскраске графика. Наименьшее количество цветов, необходимое для раскраски графа G, называется его хроматическим числом этого графа. Задача раскраски графа - это проблема NP Complete.
Метод раскраски графика
Шаги, необходимые для раскраски графа G с числом вершин n, следующие:
Step 1 - Расположите вершины графа в определенном порядке.
Step 2 - Выберите первую вершину и раскрасьте ее первым цветом.
Step 3- Выберите следующую вершину и раскрасьте ее цветом с наименьшим номером, который не был окрашен ни на одной из смежных с ней вершин. Если все соседние вершины окрашены этим цветом, присвойте ему новый цвет. Повторяйте этот шаг, пока все вершины не будут окрашены.
Example
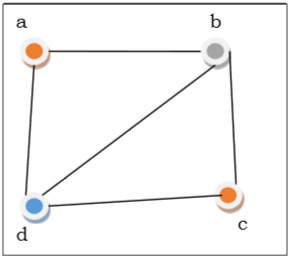
На приведенном выше рисунке сначала вершина $ a $ окрашена в красный цвет. Поскольку смежные вершины вершины a снова смежны, вершина $ b $ и вершина $ d $ окрашены в разные цвета, зеленый и синий соответственно. Тогда вершина $ c $ окрашивается в красный цвет, так как никакая смежная вершина $ c $ не окрашена в красный цвет. Следовательно, мы можем раскрасить график в 3 цвета. Следовательно, хроматическое число графа равно 3.
Применение раскраски графиков
Некоторые приложения раскраски графа включают -
- Размещение регистра
- Раскраска карты
- Проверка двудольного графа
- Присвоение мобильной радиочастоты
- Составление расписания и др.
Обход графа
Обход графа - это проблема посещения всех вершин графа в некотором систематическом порядке. В основном есть два способа пересечь граф.
- Поиск в ширину
- Поиск в глубину
Поиск в ширину
Поиск в ширину (BFS) начинается с начальной вершины уровня 0 $ X $ графа $ G $. Затем мы посещаем все вершины, которые являются соседями $ X $. После посещения мы помечаем вершины как «посещенные» и помещаем их на уровень 1. Затем мы начинаем с вершин уровня 1 и применяем тот же метод к каждой вершине уровня 1 и так далее. Обход BFS завершается после посещения каждой вершины графа.
BFS Algorithm
Идея состоит в том, чтобы посетить все соседние вершины перед посещением других соседних вершин соседних вершин.
Инициализировать состояние всех узлов как «Готово».
Поместите исходную вершину в очередь и измените ее статус на «Ожидание».
Повторяйте следующие два шага, пока очередь не станет пустой -
Удалите первую вершину из очереди и пометьте ее как «Посещенная».
Добавить в конец очереди всех соседей удаленной вершины со статусом «Готов». Отметьте их статус как «Ожидание».
Problem
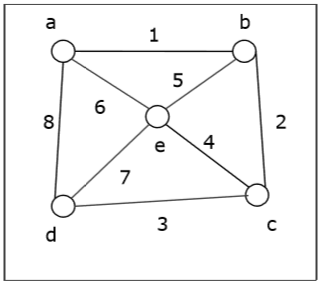
Давайте возьмем граф (исходная вершина - 'a') и применим алгоритм BFS, чтобы узнать порядок обхода.
Solution -
Инициализировать статус всех вершин как «Готово».
Помещенный в очереди и изменить свой статус «Ожидание».
Удалите объект из очереди, отметив его как «Посещенный».
Добавьте соседей a в состоянии «Готов» b, d и e в конец очереди и пометьте их как «Ожидание».
Удалите b из очереди, пометьте его как «Посещенный», поместите его «Готового» соседа c в конец очереди и отметьте c как «Ожидание».
Удалите d из очереди и отметьте его как «Посещенный». У него нет соседа в состоянии «Готов».
Удалите e из очереди и отметьте его как «Посещенный». У него нет соседа в состоянии «Готов».
Удалите c из очереди и отметьте его как «Посещенный». У него нет соседа в состоянии «Готов».
Очередь пуста, остановитесь.
Итак, порядок обхода -
$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $
Альтернативные порядки обхода:
$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Или $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $
Или $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $
Или $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Или $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Application of BFS
- Поиск кратчайшего пути
- Минимальное остовное дерево для невзвешенного графа
- Система навигации GPS
- Обнаружение циклов в неориентированном графе
- Поиск всех узлов в одном связном компоненте
Complexity Analysis
Пусть $ G (V, E) $ - граф с $ | V | $ числом вершин и $ | E | $ числом ребер. Если алгоритм поиска в ширину посещает каждую вершину в графе и проверяет каждое ребро, то его временная сложность будет -
$$ O (| V | + | E |). O (| E |) $$
Оно может варьироваться от $ O (1) $ до $ O (| V2 |) $.
Поиск в глубину
Алгоритм поиска в глубину (DFS) начинается с вершины $ v $, затем он переходит к соседней вершине (скажем, x), которая не была посещена ранее и помечается как "посещенная", и продолжается со смежной вершиной $ x $ и скоро.
Если в какой-либо вершине он обнаруживает, что все соседние вершины посещены, он возвращается, пока не найдет первую вершину, имеющую смежную вершину, которая не была пройдена ранее. Затем он проходит эту вершину, продолжает движение по соседним вершинам, пока не пройдет все посещенные вершины, и ему снова придется вернуться назад. Таким образом, он пройдет все вершины, достижимые из начальной вершины $ v $.
DFS Algorithm
Идея состоит в том, чтобы посетить все соседние вершины соседней вершины перед посещением других соседних вершин.
Инициализировать статус всех узлов как «Готово»
Поместите исходную вершину в стек и измените ее статус на «Ожидание»
Повторяйте следующие два шага, пока стек не станет пустым -
Вытащите верхнюю вершину из стека и пометьте ее как «Посещенная».
Поместите на вершину стека всех соседей удаленной вершины со статусом «Готово». Отметьте их статус как «Ожидание».
Problem
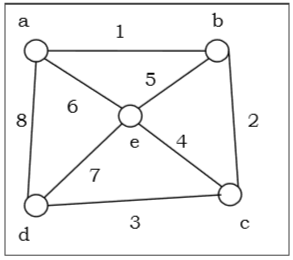
Давайте возьмем граф (исходная вершина - 'a') и применим алгоритм DFS, чтобы узнать порядок обхода.
Solution
Инициализировать статус всех вершин как «Готово».
Нажмите в стек и изменить свой статус «Ожидание».
Поп и пометить его как «посетили».
Переместите соседей a в состояние «Готово» e, d и b в верхнюю часть стека и отметьте их как «Ожидание».
Извлечь b из стека, пометить его как «Посещено», поместить его «Готовый» сосед c в стек.
Извлеките c из стопки и пометьте ее как «Посещено». У него нет «готового» соседа.
Извлечь d из стопки и пометить ее как «Посещено». У него нет «готового» соседа.
Поп - е из стека и пометить его как «посетили». У него нет «готового» соседа.
Стек пуст. Так что остановись.
Итак, порядок обхода -
$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $
Альтернативные порядки обхода:
$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $
Или $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $
Или $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Или $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $
Или $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $
Complexity Analysis
Пусть $ G (V, E) $ - граф с $ | V | $ числом вершин и $ | E | $ числом ребер. Если алгоритм DFS посещает каждую вершину в графе и проверяет каждое ребро, то временная сложность равна -
$$ \ circledash (| V | + | E |) $$
Applications
- Обнаружение цикла на графике
- Найти топологическую сортировку
- Чтобы проверить, является ли граф двудольным
- Поиск связанных компонентов
- Нахождение мостов графа
- Обнаружение двусторонней связи в графиках
- Решение задачи Knight's Tour
- Решение головоломок одним решением