Дискретная математика - отношения
Всякий раз, когда обсуждаются наборы, следующим возникает вопрос о взаимоотношениях между элементами наборов. Relations могут существовать между объектами одного набора или между объектами двух или более наборов.
Определение и свойства
Бинарное отношение R от множества x до y (записанное как $ xRy $ или $ R (x, y) $) является подмножеством декартова произведения $ x \ times y $. Если упорядоченная пара G перевернута, отношение также изменяется.
Обычно n-арное отношение R между множествами $ A_1, \ dots, \ и \ A_n $ является подмножеством n-арного произведения $ A_1 \ times \ dots \ times A_n $. Минимальная мощность отношения R равна нулю, а максимальная в этом случае равна $ n ^ 2 $.
Бинарное отношение R на одном множестве A является подмножеством $ A \ times A $.
Для двух различных наборов, A и B, имеющих мощности m и n соответственно, максимальная мощность отношения R от A к B равна mn .
Домен и диапазон
Если есть два множества A и B, а отношение R имеет пару порядков (x, y), то -
В domainR, Dom (R), есть множество $ \ lbrace x \: | \: (x, y) \ in R \: для \: some \: y \: in \: B \ rbrace $
В range R, Ran (R), является множеством $ \ lbrace y \: | \: (x, y) \ in R \: для \: some \: x \: in \: A \ rbrace $
Примеры
Пусть $ A = \ lbrace 1, 2, 9 \ rbrace $ и $ B = \ lbrace 1, 3, 7 \ rbrace $
Случай 1 - Если отношение R 'равно', то $ R = \ lbrace (1, 1), (3, 3) \ rbrace $
Dom (R) = $ \ lbrace 1, 3 \ rbrace, Ran (R) = \ lbrace 1, 3 \ rbrace $
Случай 2 - Если отношение R 'меньше', то $ R = \ lbrace (1, 3), (1, 7), (2, 3), (2, 7) \ rbrace $
Dom (R) = $ \ lbrace 1, 2 \ rbrace, Ran (R) = \ lbrace 3, 7 \ rbrace $
Случай 3 - Если отношение R 'больше', то $ R = \ lbrace (2, 1), (9, 1), (9, 3), (9, 7) \ rbrace $
Dom (R) = $ \ lbrace 2, 9 \ rbrace, Ran (R) = \ lbrace 1, 3, 7 \ rbrace $
Представление отношений с помощью графика
Отношение можно представить с помощью ориентированного графа.
Количество вершин в графе равно количеству элементов в множестве, из которого было определено отношение. Для каждой упорядоченной пары (x, y) в отношении R будет направленное ребро из вершины «x» в вершину «y». Если существует упорядоченная пара (x, x), в вершине x будет петля.
Предположим, на множестве $ S = \ lbrace 1, 2, 3 \ rbrace $ существует отношение $ R = \ lbrace (1, 1), (1,2), (3, 2) \ rbrace $, оно может быть представлен следующим графиком -
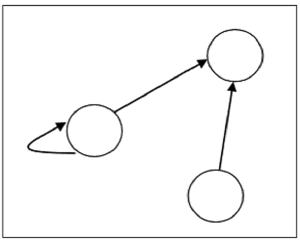
Типы отношений
В Empty Relation между множествами X и Y или на E находится пустое множество $ \ emptyset $
В Full Relation между множествами X и Y есть множество $ X \ times Y $
В Identity Relationна множестве X есть множество $ \ lbrace (x, x) | х \ в X \ rbrace $
Обратное отношение R 'отношения R определяется как - $ R' = \ lbrace (b, a) | (a, b) \ in R \ rbrace $
Example - Если $ R = \ lbrace (1, 2), (2, 3) \ rbrace $, то $ R '$ будет $ \ lbrace (2, 1), (3, 2) \ rbrace $
Отношение R на множестве A называется Reflexive если $ \ forall a \ in A $ связано с a (выполняется aRa)
Example - Отношение $ R = \ lbrace (a, a), (b, b) \ rbrace $ на множестве $ X = \ lbrace a, b \ rbrace $ рефлексивно.
Отношение R на множестве A называется Irreflexive если никакое $ a \ in A $ не связано с a (aRa не выполняется).
Example - Отношение $ R = \ lbrace (a, b), (b, a) \ rbrace $ на множестве $ X = \ lbrace a, b \ rbrace $ иррефлексивно.
Отношение R на множестве A называется Symmetric если из $ xRy $ следует $ yRx $, $ \ forall x \ in A $ и $ \ forall y \ in A $.
Example - Отношение $ R = \ lbrace (1, 2), (2, 1), (3, 2), (2, 3) \ rbrace $ на множестве $ A = \ lbrace 1, 2, 3 \ rbrace $ равно симметричный.
Отношение R на множестве A называется Anti-Symmetric если $ xRy $ и $ yRx $ влечет $ x = y \: \ forall x \ in A $ и $ \ forall y \ in A $.
Example - Отношение $ R = \ lbrace (x, y) \ к N | \: x \ leq y \ rbrace $ антисимметрично, поскольку из $ x \ leq y $ и $ y \ leq x $ следует $ x = y $ .
Отношение R на множестве A называется Transitive если из $ xRy $ и $ yRz $ следует $ xRz, \ forall x, y, z \ in A $.
Example - Отношение $ R = \ lbrace (1, 2), (2, 3), (1, 3) \ rbrace $ на множестве $ A = \ lbrace 1, 2, 3 \ rbrace $ транзитивно.
Отношение - это Equivalence Relation если он рефлексивный, симметричный и транзитивный.
Example - Соотношение $ R = \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \ rbrace $ на множестве $ A = \ lbrace 1, 2, 3 \ rbrace $ является отношением эквивалентности, поскольку оно рефлексивно, симметрично и транзитивно.