Нахождение площади прямоугольного треугольника или соответствующего ему прямоугольника
Area of a right triangle
Рассмотрим прямоугольник длиной l единиц и шириной w единиц. Нарисуем диагональ и вырежем прямоугольник. Также разрежем по диагонали, чтобы получились два прямоугольных треугольника.
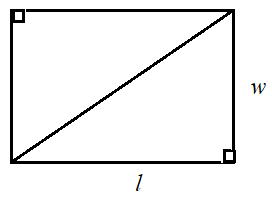
Оказалось, что два прямоугольных треугольника имеют одинаковый размер и площадь и совпадают. Таким образом, площадь каждого прямоугольного треугольника равна половине площади прямоугольника.
Площадь прямоугольного треугольника = $ \ frac {1} {2} $ площадь прямоугольника = $ \ frac {1} {2} $ l × w
Длина l прямоугольника равна основанию b прямоугольного треугольника, а ширина w прямоугольника равна высоте h прямоугольного треугольника.
So area of right triangle = $\mathbf{\frac{1}{2}}$ l × w = $\mathbf{\frac{1}{2}}$ b × h
Площадь прямоугольного треугольника равна половине площади соответствующего прямоугольника.
Найдите площадь следующего прямоугольного треугольника и соответствующего ему прямоугольника.
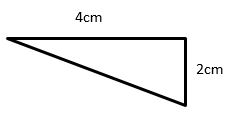
Решение
Step 1:
Площадь прямоугольного треугольника = $ \ frac {1} {2} $ × b × h; b = основание = 4; h = высота = 2
Step 2:
Площадь прямоугольного треугольника = $ \ frac {1} {2} $ × 4 × 2 = 4 квадратных см
Площадь соответствующего прямоугольника = b × h = 4 × 2 = 8 см кв.
Найдите площадь следующего прямоугольного треугольника и соответствующего ему прямоугольника.
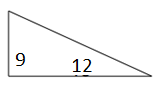
Решение
Step 1:
Площадь прямоугольного треугольника = $ \ frac {1} {2} $ × b × h; b = основание = 12; h = высота = 9
Step 2:
Площадь прямоугольного треугольника = $ \ frac {1} {2} $ × 12 × 9 = 54 квадратных единицы
Площадь соответствующего прямоугольника = b × h = 12 × 9 = 108 квадратных единиц