การวิเคราะห์ข้อมูลขนาดใหญ่ - คู่มือฉบับย่อ
ปริมาณข้อมูลที่ต้องจัดการได้เพิ่มขึ้นจนถึงระดับที่เป็นไปไม่ได้ในทศวรรษที่ผ่านมาและในขณะเดียวกันราคาของการจัดเก็บข้อมูลก็ลดลงอย่างเป็นระบบ บริษัท เอกชนและสถาบันวิจัยจะเก็บข้อมูลจำนวนเทราไบต์เกี่ยวกับการโต้ตอบของผู้ใช้ธุรกิจโซเชียลมีเดียและเซ็นเซอร์จากอุปกรณ์ต่างๆเช่นโทรศัพท์มือถือและรถยนต์ ความท้าทายของยุคนี้คือการทำความเข้าใจกับทะเลข้อมูลนี้ นี่คือที่big data analytics มาเป็นภาพ
การวิเคราะห์ข้อมูลขนาดใหญ่ส่วนใหญ่เกี่ยวข้องกับการรวบรวมข้อมูลจากแหล่งที่มาที่แตกต่างกันรวบรวมข้อมูลในลักษณะที่นักวิเคราะห์สามารถใช้งานได้และในที่สุดก็ส่งมอบผลิตภัณฑ์ข้อมูลที่เป็นประโยชน์ต่อธุรกิจขององค์กร

กระบวนการแปลงข้อมูลดิบที่ไม่มีโครงสร้างจำนวนมากซึ่งดึงมาจากแหล่งต่างๆไปยังผลิตภัณฑ์ข้อมูลที่มีประโยชน์สำหรับองค์กรถือเป็นแกนหลักของ Big Data Analytics
วงจรชีวิตการขุดข้อมูลแบบดั้งเดิม
เพื่อให้เป็นกรอบในการจัดระเบียบงานที่องค์กรต้องการและนำเสนอข้อมูลเชิงลึกที่ชัดเจนจากข้อมูลขนาดใหญ่การคิดว่าเป็นวงจรที่มีขั้นตอนต่างๆจะมีประโยชน์ มันไม่ได้เป็นเชิงเส้นหมายความว่าขั้นตอนทั้งหมดเกี่ยวข้องกัน วัฏจักรนี้มีความคล้ายคลึงกันอย่างผิวเผินกับวงจรการขุดข้อมูลแบบดั้งเดิมตามที่อธิบายไว้ในCRISP methodology.
ระเบียบวิธี CRISP-DM
CRISP-DM methodologyซึ่งย่อมาจากกระบวนการมาตรฐานข้ามอุตสาหกรรมสำหรับการขุดข้อมูลเป็นวงจรที่อธิบายถึงวิธีการที่ใช้กันทั่วไปซึ่งผู้เชี่ยวชาญด้านการขุดข้อมูลใช้เพื่อแก้ไขปัญหาในการขุดข้อมูล BI แบบเดิม ยังคงถูกใช้ในทีมขุดข้อมูล BI แบบเดิม
ดูภาพประกอบต่อไปนี้ แสดงขั้นตอนสำคัญของวัฏจักรตามที่อธิบายโดยวิธีการ CRISP-DM และความสัมพันธ์ระหว่างกันอย่างไร
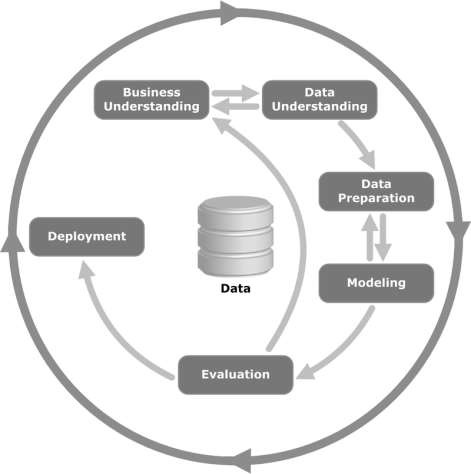
CRISP-DM เกิดขึ้นในปี 2539 และในปีหน้าได้ดำเนินการในฐานะโครงการของสหภาพยุโรปภายใต้โครงการริเริ่มการระดมทุน ESPRIT โครงการนี้นำโดย บริษัท 5 แห่ง ได้แก่ SPSS, Teradata, Daimler AG, NCR Corporation และ OHRA (บริษัท ประกันภัย) ในที่สุดโครงการก็รวมเข้ากับ SPSS วิธีการนี้มีรายละเอียดอย่างมากว่าควรระบุโครงการเหมืองข้อมูลอย่างไร
ตอนนี้ให้เราเรียนรู้เพิ่มเติมเล็กน้อยเกี่ยวกับแต่ละขั้นตอนที่เกี่ยวข้องกับวงจรชีวิต CRISP-DM -
Business Understanding- ระยะเริ่มต้นนี้มุ่งเน้นไปที่การทำความเข้าใจวัตถุประสงค์ของโครงการและข้อกำหนดจากมุมมองทางธุรกิจจากนั้นจึงแปลงความรู้นี้เป็นคำจำกัดความของปัญหาการขุดข้อมูล แผนเบื้องต้นได้รับการออกแบบมาเพื่อให้บรรลุวัตถุประสงค์ สามารถใช้รูปแบบการตัดสินใจโดยเฉพาะแบบจำลองที่สร้างขึ้นโดยใช้แบบจำลองการตัดสินใจและมาตรฐานสัญกรณ์ได้
Data Understanding - ขั้นตอนการทำความเข้าใจข้อมูลเริ่มต้นด้วยการรวบรวมข้อมูลเบื้องต้นและดำเนินการกับกิจกรรมต่างๆเพื่อทำความคุ้นเคยกับข้อมูลระบุปัญหาด้านคุณภาพของข้อมูลค้นหาข้อมูลเชิงลึกแรกของข้อมูลหรือตรวจหาชุดย่อยที่น่าสนใจเพื่อสร้างสมมติฐานสำหรับข้อมูลที่ซ่อนอยู่
Data Preparation- ขั้นตอนการเตรียมข้อมูลครอบคลุมกิจกรรมทั้งหมดในการสร้างชุดข้อมูลขั้นสุดท้าย (ข้อมูลที่จะป้อนลงในเครื่องมือการสร้างแบบจำลอง) จากข้อมูลดิบเริ่มต้น งานจัดเตรียมข้อมูลมีแนวโน้มที่จะดำเนินการหลายครั้งและไม่เป็นไปตามลำดับที่กำหนด งานรวมถึงตารางบันทึกและการเลือกแอตทริบิวต์ตลอดจนการแปลงและทำความสะอาดข้อมูลสำหรับเครื่องมือสร้างแบบจำลอง
Modeling- ในขั้นตอนนี้เทคนิคการสร้างแบบจำลองต่างๆจะถูกเลือกและนำไปใช้และพารามิเตอร์จะถูกปรับเทียบเป็นค่าที่เหมาะสมที่สุด โดยทั่วไปมีหลายเทคนิคสำหรับปัญหาประเภทการขุดข้อมูลเดียวกัน เทคนิคบางอย่างมีข้อกำหนดเฉพาะเกี่ยวกับรูปแบบของข้อมูล ดังนั้นจึงมักจะต้องย้อนกลับไปสู่ขั้นตอนการเตรียมข้อมูล
Evaluation- ในขั้นตอนนี้ในโครงการคุณได้สร้างแบบจำลอง (หรือแบบจำลอง) ที่ดูเหมือนจะมีคุณภาพสูงจากมุมมองการวิเคราะห์ข้อมูล ก่อนดำเนินการปรับใช้โมเดลขั้นสุดท้ายสิ่งสำคัญคือต้องประเมินโมเดลอย่างละเอียดและทบทวนขั้นตอนที่ดำเนินการเพื่อสร้างโมเดลเพื่อให้แน่ใจว่าโมเดลนั้นบรรลุวัตถุประสงค์ทางธุรกิจอย่างเหมาะสม
วัตถุประสงค์หลักคือเพื่อตรวจสอบว่ามีปัญหาทางธุรกิจที่สำคัญบางอย่างที่ไม่ได้รับการพิจารณาอย่างเพียงพอหรือไม่ ในตอนท้ายของขั้นตอนนี้ควรมีการตัดสินใจเกี่ยวกับการใช้ผลการขุดข้อมูล
Deployment- การสร้างแบบจำลองโดยทั่วไปไม่ใช่จุดสิ้นสุดของโครงการ แม้ว่าวัตถุประสงค์ของแบบจำลองจะเพื่อเพิ่มความรู้เกี่ยวกับข้อมูล แต่ความรู้ที่ได้รับจะต้องได้รับการจัดระเบียบและนำเสนอในรูปแบบที่เป็นประโยชน์ต่อลูกค้า
ขึ้นอยู่กับความต้องการขั้นตอนการปรับใช้อาจทำได้ง่ายเพียงแค่สร้างรายงานหรือซับซ้อนพอ ๆ กับการใช้การให้คะแนนข้อมูลที่ทำซ้ำได้ (เช่นการจัดสรรเซ็กเมนต์) หรือกระบวนการขุดข้อมูล
ในหลายกรณีจะเป็นลูกค้าไม่ใช่นักวิเคราะห์ข้อมูลที่จะดำเนินการตามขั้นตอนการปรับใช้ แม้ว่านักวิเคราะห์จะปรับใช้โมเดล แต่สิ่งสำคัญคือลูกค้าต้องเข้าใจล่วงหน้าถึงการกระทำที่จะต้องดำเนินการเพื่อให้สามารถใช้ประโยชน์จากโมเดลที่สร้างขึ้นได้จริง
ระเบียบวิธี SEMMA
SEMMA เป็นอีกวิธีหนึ่งที่พัฒนาโดย SAS สำหรับการสร้างแบบจำลองการขุดข้อมูล ย่อมาจากSกว้างขวาง Explore, Mโอดิฟาย Model และ Asses. นี่คือคำอธิบายสั้น ๆ ของขั้นตอน -
Sample- กระบวนการเริ่มต้นด้วยการสุ่มตัวอย่างข้อมูลเช่นการเลือกชุดข้อมูลสำหรับการสร้างแบบจำลอง ชุดข้อมูลควรมีขนาดใหญ่พอที่จะมีข้อมูลเพียงพอในการดึงข้อมูล แต่มีขนาดเล็กพอที่จะใช้อย่างมีประสิทธิภาพ ระยะนี้ยังเกี่ยวข้องกับการแบ่งข้อมูล
Explore - ระยะนี้ครอบคลุมความเข้าใจของข้อมูลโดยการค้นหาความสัมพันธ์ที่คาดการณ์ไว้และไม่คาดคิดระหว่างตัวแปรและความผิดปกติด้วยความช่วยเหลือของการแสดงข้อมูล
Modify - ขั้นตอนการปรับเปลี่ยนประกอบด้วยวิธีการในการเลือกสร้างและแปลงตัวแปรเพื่อเตรียมการสร้างแบบจำลองข้อมูล
Model - ในขั้นตอนของโมเดลมุ่งเน้นไปที่การใช้เทคนิคการสร้างแบบจำลองต่างๆ (การขุดข้อมูล) กับตัวแปรที่เตรียมไว้เพื่อสร้างแบบจำลองที่อาจให้ผลลัพธ์ที่ต้องการ
Assess - การประเมินผลการสร้างแบบจำลองแสดงความน่าเชื่อถือและประโยชน์ของแบบจำลองที่สร้างขึ้น
ความแตกต่างที่สำคัญระหว่าง CRISM – DM และ SEMMA คือ SEMMA มุ่งเน้นไปที่ด้านการสร้างแบบจำลองในขณะที่ CRISP-DM ให้ความสำคัญกับขั้นตอนของวงจรก่อนการสร้างแบบจำลองเช่นการทำความเข้าใจปัญหาทางธุรกิจที่จะแก้ไขทำความเข้าใจและประมวลผลข้อมูลล่วงหน้า ใช้เป็นอินพุตตัวอย่างเช่นอัลกอริทึมการเรียนรู้ของเครื่อง
วงจรชีวิตข้อมูลขนาดใหญ่
ในบริบทข้อมูลขนาดใหญ่ในปัจจุบันแนวทางก่อนหน้านี้อาจไม่สมบูรณ์หรือไม่เหมาะสม ตัวอย่างเช่นวิธีการของ SEMMA ไม่คำนึงถึงการรวบรวมข้อมูลโดยสิ้นเชิงและการประมวลผลล่วงหน้าของแหล่งข้อมูลต่างๆ โดยปกติขั้นตอนเหล่านี้ถือเป็นงานส่วนใหญ่ในโครงการข้อมูลขนาดใหญ่ที่ประสบความสำเร็จ
วงจรการวิเคราะห์ข้อมูลขนาดใหญ่สามารถอธิบายได้ในขั้นตอนต่อไปนี้ -
- นิยามปัญหาทางธุรกิจ
- Research
- การประเมินทรัพยากรมนุษย์
- การได้มาของข้อมูล
- ข้อมูล Munging
- การจัดเก็บข้อมูล
- การวิเคราะห์ข้อมูลเชิงสำรวจ
- การเตรียมข้อมูลสำหรับการสร้างแบบจำลองและการประเมิน
- Modeling
- Implementation
ในส่วนนี้เราจะให้ความสำคัญกับแต่ละขั้นตอนของวงจรชีวิตข้อมูลขนาดใหญ่
นิยามปัญหาทางธุรกิจ
นี่เป็นจุดที่พบบ่อยในวงจรชีวิตการวิเคราะห์ BI และข้อมูลขนาดใหญ่แบบดั้งเดิม โดยปกติจะเป็นขั้นตอนที่ไม่สำคัญของโครงการข้อมูลขนาดใหญ่เพื่อกำหนดปัญหาและประเมินอย่างถูกต้องว่าอาจมีโอกาสได้รับมากเพียงใดสำหรับองค์กร ดูเหมือนชัดเจนที่จะพูดถึงเรื่องนี้ แต่ต้องมีการประเมินว่าผลกำไรและต้นทุนที่คาดหวังของโครงการคืออะไร
การวิจัย
วิเคราะห์สิ่งที่ บริษัท อื่นทำในสถานการณ์เดียวกัน สิ่งนี้เกี่ยวข้องกับการมองหาโซลูชันที่เหมาะสมกับ บริษัท ของคุณแม้ว่าจะเกี่ยวข้องกับการปรับใช้โซลูชันอื่น ๆ ให้เข้ากับทรัพยากรและข้อกำหนดที่ บริษัท ของคุณมี ในขั้นตอนนี้ควรกำหนดวิธีการสำหรับขั้นตอนในอนาคต
การประเมินทรัพยากรมนุษย์
เมื่อกำหนดปัญหาแล้วก็สมเหตุสมผลที่จะวิเคราะห์ต่อไปว่าเจ้าหน้าที่ปัจจุบันสามารถดำเนินโครงการได้สำเร็จหรือไม่ ทีม BI แบบดั้งเดิมอาจไม่สามารถส่งมอบโซลูชันที่ดีที่สุดให้กับทุกขั้นตอนได้ดังนั้นจึงควรพิจารณาก่อนเริ่มโครงการหากจำเป็นต้องจ้างบุคคลภายนอกในส่วนหนึ่งของโครงการหรือจ้างคนเพิ่ม
การได้มาของข้อมูล
ส่วนนี้เป็นกุญแจสำคัญในวงจรชีวิตข้อมูลขนาดใหญ่ กำหนดว่าจะต้องใช้โปรไฟล์ประเภทใดในการส่งมอบผลิตภัณฑ์ข้อมูลที่เป็นผลลัพธ์ การรวบรวมข้อมูลเป็นขั้นตอนที่ไม่สำคัญของกระบวนการ โดยปกติจะเกี่ยวข้องกับการรวบรวมข้อมูลที่ไม่มีโครงสร้างจากแหล่งต่างๆ ในการยกตัวอย่างอาจเกี่ยวข้องกับการเขียนโปรแกรมรวบรวมข้อมูลเพื่อดึงบทวิจารณ์จากเว็บไซต์ สิ่งนี้เกี่ยวข้องกับการจัดการกับข้อความซึ่งโดยปกติแล้วอาจเป็นภาษาที่แตกต่างกันซึ่งต้องใช้เวลานานพอสมควรในการทำให้เสร็จสมบูรณ์
ข้อมูล Munging
เมื่อดึงข้อมูลออกมาเช่นจากเว็บแล้วข้อมูลนั้นจะต้องถูกจัดเก็บในรูปแบบที่ใช้งานง่าย หากต้องการดูตัวอย่างบทวิจารณ์ต่อไปสมมติว่ามีการดึงข้อมูลจากไซต์ต่างๆซึ่งแต่ละไซต์มีการแสดงข้อมูลที่แตกต่างกัน
สมมติว่าแหล่งข้อมูลหนึ่งให้บทวิจารณ์ในแง่ของการให้คะแนนเป็นดาวดังนั้นจึงเป็นไปได้ที่จะอ่านสิ่งนี้เป็นการแมปสำหรับตัวแปรการตอบสนอง y ∈ {1, 2, 3, 4, 5}. แหล่งข้อมูลอื่นให้การตรวจสอบโดยใช้ระบบลูกศรสองอันระบบหนึ่งสำหรับการลงคะแนนและอีกระบบหนึ่งสำหรับการลงคะแนน นี่จะบ่งบอกถึงตัวแปรการตอบสนองของแบบฟอร์มy ∈ {positive, negative}.
ในการรวมแหล่งข้อมูลทั้งสองแหล่งต้องมีการตัดสินใจเพื่อให้การแสดงการตอบสนองทั้งสองนี้เทียบเท่ากัน ซึ่งอาจเกี่ยวข้องกับการแปลงการแสดงการตอบสนองของแหล่งข้อมูลแรกเป็นรูปแบบที่สองโดยพิจารณาว่าหนึ่งดาวเป็นค่าลบและห้าดาวเป็นค่าบวก กระบวนการนี้มักจะต้องมีการจัดสรรเวลาจำนวนมากเพื่อให้ได้คุณภาพที่ดี
การจัดเก็บข้อมูล
เมื่อประมวลผลข้อมูลแล้วบางครั้งจำเป็นต้องจัดเก็บไว้ในฐานข้อมูล เทคโนโลยีข้อมูลขนาดใหญ่มีทางเลือกมากมายเกี่ยวกับประเด็นนี้ ทางเลือกที่พบบ่อยที่สุดคือการใช้ Hadoop File System สำหรับพื้นที่จัดเก็บข้อมูลที่ให้ SQL เวอร์ชัน จำกัด แก่ผู้ใช้ซึ่งเรียกว่า HIVE Query Language สิ่งนี้ช่วยให้งานการวิเคราะห์ส่วนใหญ่สามารถทำได้ในลักษณะเดียวกันกับที่ทำในคลังข้อมูล BI แบบดั้งเดิมจากมุมมองของผู้ใช้ ตัวเลือกการจัดเก็บอื่น ๆ ที่ต้องพิจารณา ได้แก่ MongoDB, Redis และ SPARK
ขั้นตอนของวงจรนี้เกี่ยวข้องกับความรู้ด้านทรัพยากรมนุษย์ในแง่ของความสามารถในการใช้สถาปัตยกรรมที่แตกต่างกัน คลังข้อมูลแบบดั้งเดิมเวอร์ชันดัดแปลงยังคงถูกใช้ในแอปพลิเคชันขนาดใหญ่ ตัวอย่างเช่น teradata และ IBM นำเสนอฐานข้อมูล SQL ที่สามารถจัดการข้อมูลจำนวนเทราไบต์ โซลูชันโอเพนซอร์สเช่น postgreSQL และ MySQL ยังคงถูกใช้สำหรับแอปพลิเคชันขนาดใหญ่
แม้ว่าจะมีความแตกต่างกันในการทำงานของการจัดเก็บข้อมูลที่แตกต่างกันในพื้นหลัง แต่จากฝั่งไคลเอ็นต์โซลูชันส่วนใหญ่จะมี SQL API ดังนั้นการมีความเข้าใจที่ดีเกี่ยวกับ SQL จึงยังคงเป็นทักษะสำคัญที่ต้องมีสำหรับการวิเคราะห์ข้อมูลขนาดใหญ่
ขั้นตอนนี้เบื้องต้นน่าจะเป็นหัวข้อที่สำคัญที่สุดในทางปฏิบัติไม่เป็นความจริง มันไม่ได้เป็นเวทีสำคัญ เป็นไปได้ที่จะใช้โซลูชันข้อมูลขนาดใหญ่ที่จะทำงานร่วมกับข้อมูลแบบเรียลไทม์ดังนั้นในกรณีนี้เราจำเป็นต้องรวบรวมข้อมูลเพื่อพัฒนาแบบจำลองจากนั้นจึงนำไปใช้แบบเรียลไทม์ ดังนั้นจึงไม่จำเป็นต้องจัดเก็บข้อมูลอย่างเป็นทางการเลย
การวิเคราะห์ข้อมูลเชิงสำรวจ
เมื่อข้อมูลได้รับการทำความสะอาดและจัดเก็บในลักษณะที่สามารถดึงข้อมูลเชิงลึกออกมาได้แล้วขั้นตอนการสำรวจข้อมูลจะมีผลบังคับ วัตถุประสงค์ของขั้นตอนนี้คือการทำความเข้าใจข้อมูลโดยปกติจะทำด้วยเทคนิคทางสถิติและการลงจุดข้อมูลด้วย นี่เป็นขั้นตอนที่ดีในการประเมินว่าคำจำกัดความของปัญหานั้นสมเหตุสมผลหรือเป็นไปได้
การเตรียมข้อมูลสำหรับการสร้างแบบจำลองและการประเมิน
ขั้นตอนนี้เกี่ยวข้องกับการปรับรูปร่างข้อมูลที่ล้างแล้วที่ดึงมาก่อนหน้านี้และใช้การประมวลผลล่วงหน้าทางสถิติสำหรับการใส่ค่าที่ขาดหายไปการตรวจหาค่าผิดปกติการทำให้เป็นมาตรฐานการแยกคุณลักษณะและการเลือกคุณสมบัติ
การสร้างแบบจำลอง
ขั้นตอนก่อนหน้านี้ควรมีการสร้างชุดข้อมูลหลายชุดสำหรับการฝึกอบรมและการทดสอบตัวอย่างเช่นแบบจำลองการคาดการณ์ ขั้นตอนนี้เกี่ยวข้องกับการลองใช้โมเดลต่างๆและรอคอยที่จะแก้ไขปัญหาทางธุรกิจที่อยู่ในมือ ในทางปฏิบัติเป็นที่ต้องการโดยปกติที่โมเดลจะให้ข้อมูลเชิงลึกเกี่ยวกับธุรกิจ ในที่สุดโมเดลที่ดีที่สุดหรือการรวมกันของแบบจำลองจะถูกเลือกโดยประเมินประสิทธิภาพของชุดข้อมูลด้านซ้าย
การนำไปใช้
ในขั้นตอนนี้ผลิตภัณฑ์ข้อมูลที่พัฒนาจะถูกนำไปใช้ในท่อส่งข้อมูลของ บริษัท สิ่งนี้เกี่ยวข้องกับการตั้งค่ารูปแบบการตรวจสอบความถูกต้องในขณะที่ผลิตภัณฑ์ข้อมูลกำลังทำงานเพื่อติดตามประสิทธิภาพ ตัวอย่างเช่นในกรณีของการใช้แบบจำลองเชิงคาดการณ์ขั้นตอนนี้จะเกี่ยวข้องกับการใช้โมเดลกับข้อมูลใหม่และเมื่อมีการตอบสนองแล้วให้ประเมินโมเดล
ในแง่ของวิธีการการวิเคราะห์ข้อมูลขนาดใหญ่แตกต่างอย่างมีนัยสำคัญจากวิธีการทางสถิติแบบดั้งเดิมของการออกแบบการทดลอง การวิเคราะห์เริ่มต้นด้วยข้อมูล โดยปกติเราสร้างแบบจำลองข้อมูลด้วยวิธีการอธิบายการตอบสนอง วัตถุประสงค์ของแนวทางนี้คือการทำนายพฤติกรรมการตอบสนองหรือทำความเข้าใจว่าตัวแปรอินพุตเกี่ยวข้องกับการตอบสนองอย่างไร โดยปกติในการออกแบบการทดลองทางสถิติจะมีการพัฒนาการทดลองและดึงข้อมูลมาเป็นผลลัพธ์ สิ่งนี้ช่วยให้สามารถสร้างข้อมูลในลักษณะที่สามารถใช้โดยแบบจำลองทางสถิติซึ่งสมมติฐานบางอย่างมีเช่นความเป็นอิสระความเป็นปกติและการสุ่ม
ในการวิเคราะห์ข้อมูลขนาดใหญ่เราจะนำเสนอข้อมูล เราไม่สามารถออกแบบการทดลองที่ตอบสนองแบบจำลองทางสถิติที่เราชื่นชอบได้ ในแอปพลิเคชันการวิเคราะห์ขนาดใหญ่จำเป็นต้องใช้งานจำนวนมาก (ปกติ 80% ของความพยายาม) เพื่อทำความสะอาดข้อมูลดังนั้นจึงสามารถใช้โมเดลการเรียนรู้ของเครื่องได้
เราไม่มีวิธีการเฉพาะที่จะปฏิบัติตามในแอปพลิเคชันขนาดใหญ่จริง โดยปกติเมื่อกำหนดปัญหาทางธุรกิจแล้วจำเป็นต้องมีขั้นตอนการวิจัยเพื่อออกแบบวิธีการที่จะใช้ อย่างไรก็ตามหลักเกณฑ์ทั่วไปเกี่ยวข้องที่จะกล่าวถึงและนำไปใช้กับปัญหาเกือบทั้งหมด
งานที่สำคัญที่สุดอย่างหนึ่งในการวิเคราะห์ข้อมูลขนาดใหญ่คือ statistical modelingหมายถึงการจำแนกประเภทหรือปัญหาการถดถอยภายใต้การดูแลและไม่ได้รับการดูแล เมื่อข้อมูลได้รับการทำความสะอาดและประมวลผลล่วงหน้าพร้อมใช้งานสำหรับการสร้างแบบจำลองแล้วควรใช้ความระมัดระวังในการประเมินแบบจำลองที่แตกต่างกันโดยมีเมตริกการสูญเสียที่สมเหตุสมผลจากนั้นเมื่อใช้แบบจำลองแล้วควรมีการรายงานการประเมินและผลลัพธ์เพิ่มเติม ข้อผิดพลาดที่พบบ่อยในการสร้างแบบจำลองเชิงคาดการณ์คือการใช้แบบจำลองเท่านั้นและอย่าวัดประสิทธิภาพของโมเดล
ดังที่ได้กล่าวไว้ในวงจรชีวิตของข้อมูลขนาดใหญ่ผลิตภัณฑ์ข้อมูลที่เป็นผลมาจากการพัฒนาผลิตภัณฑ์ข้อมูลขนาดใหญ่นั้นส่วนใหญ่มีดังต่อไปนี้ -
Machine learning implementation - นี่อาจเป็นอัลกอริทึมการจำแนกแบบจำลองการถดถอยหรือแบบจำลองการแบ่งส่วน
Recommender system - มีวัตถุประสงค์เพื่อพัฒนาระบบที่แนะนำทางเลือกตามพฤติกรรมของผู้ใช้ Netflix เป็นตัวอย่างลักษณะเฉพาะของผลิตภัณฑ์ข้อมูลนี้ซึ่งแนะนำให้ใช้ภาพยนตร์เรื่องอื่น ๆ ตามการให้คะแนนของผู้ใช้
Dashboard- โดยปกติธุรกิจจำเป็นต้องใช้เครื่องมือในการแสดงภาพข้อมูลรวม แดชบอร์ดเป็นกลไกแบบกราฟิกเพื่อให้สามารถเข้าถึงข้อมูลนี้ได้
Ad-Hoc analysis - โดยปกติพื้นที่ธุรกิจจะมีคำถามสมมติฐานหรือตำนานที่สามารถตอบได้ในการวิเคราะห์แบบเฉพาะกิจกับข้อมูล
ในองค์กรขนาดใหญ่ในการพัฒนาโครงการข้อมูลขนาดใหญ่ให้ประสบความสำเร็จจำเป็นต้องมีฝ่ายบริหารสำรองข้อมูลโครงการ โดยปกติจะเกี่ยวข้องกับการหาวิธีแสดงข้อดีทางธุรกิจของโครงการ เราไม่มีวิธีแก้ปัญหาเฉพาะในการค้นหาผู้สนับสนุนโครงการ แต่มีแนวทางบางประการด้านล่างนี้ -
ตรวจสอบว่าใครเป็นผู้สนับสนุนโครงการอื่นที่คล้ายคลึงกับโครงการที่คุณสนใจ
การมีผู้ติดต่อส่วนตัวในตำแหน่งผู้บริหารที่สำคัญจะช่วยได้ดังนั้นการติดต่อใด ๆ จะถูกกระตุ้นหากโครงการมีแนวโน้ม
ใครจะได้รับประโยชน์จากโครงการของคุณ? ใครจะเป็นลูกค้าของคุณเมื่อโครงการอยู่ระหว่างดำเนินการ
พัฒนาข้อเสนอที่เรียบง่ายชัดเจนและออกจากระบบและแบ่งปันกับผู้มีบทบาทสำคัญในองค์กรของคุณ
วิธีที่ดีที่สุดในการค้นหาผู้สนับสนุนสำหรับโครงการคือการทำความเข้าใจปัญหาและสิ่งที่จะเป็นผลลัพธ์ของผลิตภัณฑ์ข้อมูลเมื่อดำเนินการแล้ว ความเข้าใจนี้จะช่วยให้ผู้บริหารเข้าใจถึงความสำคัญของโครงการข้อมูลขนาดใหญ่
นักวิเคราะห์ข้อมูลมีโปรไฟล์ที่มุ่งเน้นการรายงานมีประสบการณ์ในการแยกและวิเคราะห์ข้อมูลจากคลังข้อมูลแบบดั้งเดิมโดยใช้ SQL โดยปกติงานของพวกเขาจะอยู่ด้านข้างของการจัดเก็บข้อมูลหรือในการรายงานผลทางธุรกิจทั่วไป คลังข้อมูลไม่ใช่เรื่องง่าย แต่แตกต่างจากสิ่งที่นักวิทยาศาสตร์ข้อมูลทำ
หลายองค์กรพยายามอย่างหนักเพื่อหานักวิทยาศาสตร์ข้อมูลที่มีความสามารถในตลาด อย่างไรก็ตามเป็นความคิดที่ดีที่จะเลือกนักวิเคราะห์ข้อมูลที่คาดหวังและสอนทักษะที่เกี่ยวข้องในการเป็นนักวิทยาศาสตร์ข้อมูล นี่ไม่ใช่งานเล็กน้อยและโดยปกติจะเกี่ยวข้องกับผู้ที่สำเร็จการศึกษาระดับปริญญาโทในสาขาเชิงปริมาณ แต่ก็เป็นทางเลือกที่ทำได้อย่างแน่นอน ทักษะพื้นฐานที่นักวิเคราะห์ข้อมูลที่มีความสามารถต้องมีดังต่อไปนี้ -
- ความเข้าใจในธุรกิจ
- การเขียนโปรแกรม SQL
- การออกแบบและการใช้งานรายงาน
- การพัฒนาแดชบอร์ด
บทบาทของนักวิทยาศาสตร์ข้อมูลมักเกี่ยวข้องกับงานต่างๆเช่นการสร้างแบบจำลองเชิงคาดการณ์การพัฒนาอัลกอริธึมการแบ่งกลุ่มระบบผู้แนะนำกรอบการทดสอบ A / B และมักจะทำงานกับข้อมูลดิบที่ไม่มีโครงสร้าง
ลักษณะงานของพวกเขาต้องการความเข้าใจอย่างลึกซึ้งเกี่ยวกับคณิตศาสตร์สถิติประยุกต์และการเขียนโปรแกรม มีทักษะบางอย่างที่พบบ่อยระหว่างนักวิเคราะห์ข้อมูลและนักวิทยาศาสตร์ข้อมูลตัวอย่างเช่นความสามารถในการสืบค้นฐานข้อมูล ทั้งวิเคราะห์ข้อมูล แต่การตัดสินใจของนักวิทยาศาสตร์ข้อมูลอาจส่งผลกระทบมากกว่าในองค์กร
นี่คือชุดทักษะที่นักวิทยาศาสตร์ข้อมูลจำเป็นต้องมี -
- การเขียนโปรแกรมในแพ็คเกจทางสถิติเช่น R, Python, SAS, SPSS หรือ Julia
- สามารถทำความสะอาดแยกและสำรวจข้อมูลจากแหล่งต่างๆ
- การวิจัยการออกแบบและการใช้แบบจำลองทางสถิติ
- ความรู้เชิงลึกทางสถิติคณิตศาสตร์และวิทยาศาสตร์คอมพิวเตอร์
ในการวิเคราะห์ข้อมูลขนาดใหญ่โดยปกติผู้คนมักสับสนระหว่างบทบาทของนักวิทยาศาสตร์ข้อมูลกับสถาปนิกข้อมูล ในความเป็นจริงความแตกต่างค่อนข้างง่าย สถาปนิกข้อมูลเป็นผู้กำหนดเครื่องมือและสถาปัตยกรรมที่ข้อมูลจะถูกจัดเก็บในขณะที่นักวิทยาศาสตร์ข้อมูลใช้สถาปัตยกรรมนี้ แน่นอนว่านักวิทยาศาสตร์ข้อมูลควรสามารถตั้งค่าเครื่องมือใหม่ ๆ ได้หากจำเป็นสำหรับโครงการเฉพาะกิจ แต่คำจำกัดความและการออกแบบโครงสร้างพื้นฐานไม่ควรเป็นส่วนหนึ่งของงานของเขา
เราจะพัฒนาโครงการผ่านบทช่วยสอนนี้ แต่ละบทที่ตามมาในบทช่วยสอนนี้เกี่ยวข้องกับส่วนหนึ่งของโครงการขนาดใหญ่ในส่วนโครงการขนาดเล็ก นี่เป็นส่วนบทช่วยสอนที่ประยุกต์ใช้ซึ่งจะช่วยให้คุณเผชิญกับปัญหาในโลกแห่งความเป็นจริง ในกรณีนี้เราจะเริ่มต้นด้วยการกำหนดปัญหาของโครงการ
คำอธิบายโครงการ
โครงการนี้มีวัตถุประสงค์เพื่อพัฒนารูปแบบการเรียนรู้ของเครื่องเพื่อทำนายเงินเดือนรายชั่วโมงของผู้คนโดยใช้ข้อความประวัติย่อ (CV) เป็นข้อมูลป้อนเข้า
การใช้กรอบที่กำหนดไว้ข้างต้นการกำหนดปัญหานั้นเป็นเรื่องง่าย เราสามารถกำหนดX = {x 1 , x 2 , …, x n }เป็น CV ของผู้ใช้โดยที่แต่ละฟีเจอร์สามารถเป็นจำนวนครั้งที่คำนี้ปรากฏได้อย่างง่ายที่สุด จากนั้นคำตอบนั้นมีมูลค่าจริงเราพยายามคาดการณ์เงินเดือนรายชั่วโมงของแต่ละบุคคลเป็นดอลลาร์
ข้อพิจารณาทั้งสองนี้เพียงพอที่จะสรุปได้ว่าปัญหาที่นำเสนอสามารถแก้ไขได้ด้วยอัลกอริธึมการถดถอยภายใต้การดูแล
การกำหนดปัญหา
Problem Definitionอาจเป็นหนึ่งในขั้นตอนที่ซับซ้อนและถูกละเลยอย่างมากในไปป์ไลน์การวิเคราะห์ข้อมูลขนาดใหญ่ ในการกำหนดปัญหาที่ผลิตภัณฑ์ข้อมูลจะแก้ไขได้จำเป็นต้องมีประสบการณ์ นักวิทยาศาสตร์ข้อมูลส่วนใหญ่มีประสบการณ์น้อยหรือไม่มีเลยในขั้นตอนนี้
ปัญหาข้อมูลขนาดใหญ่ส่วนใหญ่สามารถแบ่งประเภทได้ดังต่อไปนี้ -
- การจัดประเภทภายใต้การดูแล
- การถดถอยภายใต้การดูแล
- การเรียนรู้ที่ไม่มีผู้ดูแล
- เรียนรู้การจัดอันดับ
ตอนนี้ให้เราเรียนรู้เพิ่มเติมเกี่ยวกับแนวคิดทั้งสี่นี้
การจัดประเภทภายใต้การดูแล
กำหนดเมทริกซ์ของคุณลักษณะX = {x 1 , x 2 , ... , x n }เราพัฒนารุ่น M ที่จะคาดการณ์เรียนแตกต่างกันกำหนดเป็นY = {C 1ค2 , ... , คn } ตัวอย่างเช่นจากข้อมูลการทำธุรกรรมของลูกค้าใน บริษัท ประกันภัยมีความเป็นไปได้ที่จะพัฒนารูปแบบที่จะทำนายว่าลูกค้าจะเลิกจ้างหรือไม่ ปัญหาหลังเป็นปัญหาการจัดประเภทไบนารีซึ่งมีสองคลาสหรือตัวแปรเป้าหมาย: ปั่นและไม่ปั่น
ปัญหาอื่น ๆ ที่เกี่ยวข้องกับการทำนายมากกว่าหนึ่งคลาสเราอาจสนใจที่จะทำการจดจำตัวเลขดังนั้นเวกเตอร์การตอบสนองจะถูกกำหนดเป็น: y = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}แบบจำลองที่ล้ำสมัยจะเป็นโครงข่ายประสาทเทียมแบบ Convolutional และเมทริกซ์ของคุณสมบัติจะถูกกำหนดเป็นพิกเซลของภาพ
การถดถอยภายใต้การดูแล
ในกรณีนี้นิยามปัญหาค่อนข้างคล้ายกับตัวอย่างก่อนหน้านี้ ความแตกต่างขึ้นอยู่กับการตอบสนอง ในปัญหาการถดถอยการตอบสนอง y ∈ℜซึ่งหมายความว่าการตอบสนองนั้นมีมูลค่าจริง ตัวอย่างเช่นเราสามารถพัฒนาแบบจำลองเพื่อคาดคะเนเงินเดือนรายชั่วโมงของแต่ละบุคคลได้จากคลังข้อมูลประวัติย่อของพวกเขา
การเรียนรู้ที่ไม่มีการดูแล
ผู้บริหารมักกระหายข้อมูลเชิงลึกใหม่ ๆ แบบจำลองการแบ่งกลุ่มสามารถให้ข้อมูลเชิงลึกนี้เพื่อให้ฝ่ายการตลาดสามารถพัฒนาผลิตภัณฑ์สำหรับกลุ่มต่างๆ แนวทางที่ดีในการพัฒนารูปแบบการแบ่งกลุ่มแทนที่จะนึกถึงอัลกอริทึมคือการเลือกคุณลักษณะที่เกี่ยวข้องกับการแบ่งส่วนที่ต้องการ
ตัวอย่างเช่นใน บริษัท โทรคมนาคมการแบ่งกลุ่มลูกค้าตามการใช้งานโทรศัพท์มือถือเป็นเรื่องน่าสนใจ สิ่งนี้จะเกี่ยวข้องกับการเพิกเฉยต่อคุณลักษณะที่ไม่มีส่วนเกี่ยวข้องกับวัตถุประสงค์การแบ่งส่วนและรวมเฉพาะคุณลักษณะที่ทำ ในกรณีนี้จะเป็นการเลือกฟีเจอร์ต่างๆเช่นจำนวน SMS ที่ใช้ในหนึ่งเดือนจำนวนนาทีขาเข้าและขาออกเป็นต้น
เรียนรู้การจัดอันดับ
ปัญหานี้ถือได้ว่าเป็นปัญหาการถดถอย แต่มีลักษณะเฉพาะและสมควรได้รับการรักษาแยกต่างหาก ปัญหาเกี่ยวข้องกับการรวบรวมเอกสารที่เราพยายามค้นหาคำสั่งซื้อที่เกี่ยวข้องมากที่สุดจากการสอบถาม ในการพัฒนาอัลกอริธึมการเรียนรู้ภายใต้การดูแลจำเป็นต้องติดป้ายกำกับว่าคำสั่งนั้นเกี่ยวข้องกับข้อความค้นหาอย่างไร
โปรดทราบว่าในการพัฒนาอัลกอริธึมการเรียนรู้ภายใต้การดูแลจำเป็นต้องติดป้ายกำกับข้อมูลการฝึกอบรม ซึ่งหมายความว่าในการฝึกโมเดลที่จะจดจำตัวเลขจากรูปภาพเราจำเป็นต้องติดป้ายกำกับตัวอย่างจำนวนมากด้วยมือ มีบริการเว็บที่สามารถเร่งกระบวนการนี้และมักใช้สำหรับงานนี้เช่น amazon mechanical turk ได้รับการพิสูจน์แล้วว่าอัลกอริทึมการเรียนรู้ช่วยเพิ่มประสิทธิภาพเมื่อได้รับข้อมูลมากขึ้นดังนั้นการติดฉลากตัวอย่างจำนวนมากจึงเป็นข้อบังคับในการเรียนรู้ภายใต้การดูแล
การรวบรวมข้อมูลมีบทบาทสำคัญที่สุดในวงจรข้อมูลขนาดใหญ่ อินเทอร์เน็ตมีแหล่งข้อมูลที่ไม่ จำกัด เกือบสำหรับหัวข้อต่างๆ ความสำคัญของพื้นที่นี้ขึ้นอยู่กับประเภทของธุรกิจ แต่อุตสาหกรรมดั้งเดิมสามารถได้รับแหล่งข้อมูลภายนอกที่หลากหลายและรวมเข้ากับข้อมูลธุรกรรมของพวกเขา
ตัวอย่างเช่นสมมติว่าเราต้องการสร้างระบบแนะนำร้านอาหาร ขั้นตอนแรกคือการรวบรวมข้อมูลในกรณีนี้บทวิจารณ์ร้านอาหารจากเว็บไซต์ต่างๆและจัดเก็บไว้ในฐานข้อมูล เนื่องจากเราสนใจข้อความดิบและจะใช้เพื่อการวิเคราะห์จึงไม่เกี่ยวข้องกับที่ข้อมูลสำหรับการพัฒนาโมเดลจะถูกจัดเก็บ สิ่งนี้อาจฟังดูขัดแย้งกับเทคโนโลยีหลักของข้อมูลขนาดใหญ่ แต่ในการใช้งานแอปพลิเคชันข้อมูลขนาดใหญ่เราจำเป็นต้องทำให้มันทำงานได้แบบเรียลไทม์
Twitter Mini Project
เมื่อกำหนดปัญหาแล้วขั้นตอนต่อไปนี้คือการรวบรวมข้อมูล แนวคิดโครงการย่อส่วนต่อไปนี้คือการรวบรวมข้อมูลจากเว็บและจัดโครงสร้างเพื่อใช้ในโมเดลแมชชีนเลิร์นนิง เราจะรวบรวมทวีตบางส่วนจาก twitter rest API โดยใช้ภาษาโปรแกรม R
ก่อนอื่นให้สร้างบัญชี Twitter จากนั้นทำตามคำแนะนำในไฟล์ twitteRแพคเกจวิกเน็ตต์เพื่อสร้างบัญชีผู้พัฒนา Twitter นี่คือบทสรุปของคำแนะนำเหล่านั้น -
ไปที่ https://twitter.com/apps/new และเข้าสู่ระบบ
หลังจากกรอกข้อมูลพื้นฐานแล้วให้ไปที่แท็บ "การตั้งค่า" แล้วเลือก "อ่านเขียนและเข้าถึงข้อความส่วนตัว"
อย่าลืมคลิกที่ปุ่มบันทึกหลังจากทำสิ่งนี้
ในแท็บ "รายละเอียด" จดรหัสผู้บริโภคและความลับของผู้บริโภค
ในเซสชัน R ของคุณคุณจะใช้คีย์ API และค่าลับของ API
สุดท้ายเรียกใช้สคริปต์ต่อไปนี้ สิ่งนี้จะติดตั้งไฟล์twitteR แพ็กเกจจากที่เก็บบน github
install.packages(c("devtools", "rjson", "bit64", "httr"))
# Make sure to restart your R session at this point
library(devtools)
install_github("geoffjentry/twitteR")เราสนใจที่จะรับข้อมูลที่รวมสตริง "big mac" และค้นหาว่าหัวข้อใดโดดเด่นในเรื่องนี้ ในการดำเนินการนี้ขั้นตอนแรกคือการรวบรวมข้อมูลจาก twitter ด้านล่างนี้เป็นสคริปต์ R ของเราเพื่อรวบรวมข้อมูลที่จำเป็นจาก twitter โค้ดนี้มีอยู่ในไฟล์ bda / part1 / collect_data / collect_data_twitter.R
rm(list = ls(all = TRUE)); gc() # Clears the global environment
library(twitteR)
Sys.setlocale(category = "LC_ALL", locale = "C")
### Replace the xxx’s with the values you got from the previous instructions
# consumer_key = "xxxxxxxxxxxxxxxxxxxx"
# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# Connect to twitter rest API
setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)
# Get tweets related to big mac
tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)
df <- twListToDF(tweets)
# Take a look at the data
head(df)
# Check which device is most used
sources <- sapply(tweets, function(x) x$getStatusSource())
sources <- gsub("</a>", "", sources)
sources <- strsplit(sources, ">")
sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))
source_table = table(sources)
source_table = source_table[source_table > 1]
freq = source_table[order(source_table, decreasing = T)]
as.data.frame(freq)
# Frequency
# Twitter for iPhone 71
# Twitter for Android 29
# Twitter Web Client 25
# recognia 20เมื่อรวบรวมข้อมูลแล้วเราจะมีแหล่งข้อมูลที่หลากหลายและมีลักษณะที่แตกต่างกัน ขั้นตอนที่รวดเร็วที่สุดคือการทำให้แหล่งข้อมูลเหล่านี้เป็นเนื้อเดียวกันและพัฒนาผลิตภัณฑ์ข้อมูลของเราต่อไป อย่างไรก็ตามขึ้นอยู่กับประเภทของข้อมูล เราควรถามตัวเองว่าสามารถทำให้ข้อมูลเป็นเนื้อเดียวกันได้จริงหรือไม่
บางทีแหล่งข้อมูลอาจแตกต่างกันอย่างสิ้นเชิงและข้อมูลจะสูญหายไปมากหากแหล่งข้อมูลนั้นถูกทำให้เป็นเนื้อเดียวกัน ในกรณีนี้เราสามารถคิดหาทางเลือกอื่น แหล่งข้อมูลหนึ่งสามารถช่วยฉันสร้างแบบจำลองการถดถอยและอีกแหล่งหนึ่งเป็นแบบจำลองการจำแนกได้หรือไม่ เป็นไปได้ไหมที่จะทำงานร่วมกับความแตกต่างจากความได้เปรียบของเราแทนที่จะสูญเสียข้อมูล? การตัดสินใจเหล่านี้เป็นสิ่งที่ทำให้การวิเคราะห์น่าสนใจและท้าทาย
ในกรณีของบทวิจารณ์เป็นไปได้ที่จะมีภาษาสำหรับแหล่งข้อมูลแต่ละแหล่ง อีกครั้งเรามีสองทางเลือก -
Homogenization- เกี่ยวข้องกับการแปลภาษาต่างๆเป็นภาษาที่เรามีข้อมูลมากขึ้น คุณภาพของบริการแปลเป็นที่ยอมรับได้ แต่หากเราต้องการแปลข้อมูลจำนวนมากด้วย API ค่าใช้จ่ายจะสูงมาก มีเครื่องมือซอฟต์แวร์สำหรับงานนี้ แต่ก็มีค่าใช้จ่ายสูงเช่นกัน
Heterogenization- เป็นไปได้ไหมที่จะพัฒนาโซลูชันสำหรับแต่ละภาษา เนื่องจากเป็นเรื่องง่ายในการตรวจหาภาษาของคลังข้อมูลเราจึงสามารถพัฒนาผู้แนะนำสำหรับแต่ละภาษาได้ สิ่งนี้จะเกี่ยวข้องกับการทำงานมากขึ้นในแง่ของการปรับแต่งผู้แนะนำแต่ละรายตามจำนวนภาษาที่มี แต่เป็นตัวเลือกที่ใช้ได้อย่างแน่นอนหากเรามีภาษาไม่กี่ภาษา
Twitter Mini Project
ในกรณีปัจจุบันเราจำเป็นต้องล้างข้อมูลที่ไม่มีโครงสร้างก่อนจากนั้นจึงแปลงเป็นเมทริกซ์ข้อมูลเพื่อใช้การสร้างแบบจำลองหัวข้อกับข้อมูลนั้น โดยทั่วไปเมื่อรับข้อมูลจาก twitter มีอักขระหลายตัวที่เราไม่สนใจใช้อย่างน้อยก็ในขั้นตอนแรกของกระบวนการล้างข้อมูล
ตัวอย่างเช่นหลังจากได้รับทวีตเราได้รับอักขระแปลก ๆ เหล่านี้: "<ed> <U + 00A0> <U + 00BD> <ed> <U + 00B8> <U + 008B>" สิ่งเหล่านี้อาจเป็นอิโมติคอนดังนั้นเพื่อล้างข้อมูลเราจะลบออกโดยใช้สคริปต์ต่อไปนี้ โค้ดนี้มีอยู่ในไฟล์ bda / part1 / collect_data / cleaning_data.R
rm(list = ls(all = TRUE)); gc() # Clears the global environment
source('collect_data_twitter.R')
# Some tweets
head(df$text)
[1] "I’m not a big fan of turkey but baked Mac &
cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"
[2] "@Jayoh30 Like no special sauce on a big mac. HOW"
### We are interested in the text - Let’s clean it!
# We first convert the encoding of the text from latin1 to ASCII
df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))
# Create a function to clean tweets
clean.text <- function(tx) {
tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)
tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)
tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)
tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)
tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE) return(tx) } clean_tweets <- lapply(df$text, clean.text)
# Cleaned tweets
head(clean_tweets)
[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "
[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "ขั้นตอนสุดท้ายของโครงการมินิการล้างข้อมูลคือการล้างข้อความที่เราสามารถแปลงเป็นเมทริกซ์และใช้อัลกอริทึมได้ จากข้อความที่เก็บไว้ในไฟล์clean_tweets เวกเตอร์เราสามารถแปลงเป็นเมทริกซ์ถุงคำได้อย่างง่ายดายและใช้อัลกอริทึมการเรียนรู้ที่ไม่มีผู้ดูแล
การรายงานมีความสำคัญมากในการวิเคราะห์ข้อมูลขนาดใหญ่ ทุกองค์กรต้องมีการจัดเตรียมข้อมูลอย่างสม่ำเสมอเพื่อสนับสนุนกระบวนการตัดสินใจ โดยปกติงานนี้จะได้รับการจัดการโดยนักวิเคราะห์ข้อมูลที่มีประสบการณ์ SQL และ ETL (แยกโอนและโหลด)
ทีมที่รับผิดชอบงานนี้มีหน้าที่ในการกระจายข้อมูลที่ผลิตในแผนกวิเคราะห์ข้อมูลขนาดใหญ่ไปยังพื้นที่ต่างๆขององค์กร
ตัวอย่างต่อไปนี้แสดงให้เห็นว่าการสรุปข้อมูลหมายถึงอะไร ไปที่โฟลเดอร์bda/part1/summarize_data และภายในโฟลเดอร์ให้เปิดไฟล์ summarize_data.Rprojโดยดับเบิลคลิกที่ไฟล์ จากนั้นเปิดไฟล์summarize_data.R สคริปต์และดูรหัสและปฏิบัติตามคำอธิบายที่นำเสนอ
# Install the following packages by running the following code in R.
pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')
install.packages(pkgs)ggplot2แพคเกจเหมาะสำหรับการแสดงข้อมูล data.table แพคเกจเป็นตัวเลือกที่ยอดเยี่ยมในการสรุปข้อมูลที่รวดเร็วและมีประสิทธิภาพในหน่วยความจำ R. เกณฑ์มาตรฐานล่าสุดแสดงให้เห็นว่าเร็วกว่าpandasไลบรารี python ที่ใช้สำหรับงานที่คล้ายกัน
ดูข้อมูลโดยใช้รหัสต่อไปนี้ รหัสนี้ยังมีอยู่ในbda/part1/summarize_data/summarize_data.Rproj ไฟล์.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Convert the flights data.frame to a data.table object and call it DT
DT <- as.data.table(flights)
# The data has 336776 rows and 16 columns
dim(DT)
# Take a look at the first rows
head(DT)
# year month day dep_time dep_delay arr_time arr_delay carrier
# 1: 2013 1 1 517 2 830 11 UA
# 2: 2013 1 1 533 4 850 20 UA
# 3: 2013 1 1 542 2 923 33 AA
# 4: 2013 1 1 544 -1 1004 -18 B6
# 5: 2013 1 1 554 -6 812 -25 DL
# 6: 2013 1 1 554 -4 740 12 UA
# tailnum flight origin dest air_time distance hour minute
# 1: N14228 1545 EWR IAH 227 1400 5 17
# 2: N24211 1714 LGA IAH 227 1416 5 33
# 3: N619AA 1141 JFK MIA 160 1089 5 42
# 4: N804JB 725 JFK BQN 183 1576 5 44
# 5: N668DN 461 LGA ATL 116 762 5 54
# 6: N39463 1696 EWR ORD 150 719 5 54โค้ดต่อไปนี้มีตัวอย่างการสรุปข้อมูล
### Data Summarization
# Compute the mean arrival delay
DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))]
# mean_arrival_delay
# 1: 6.895377
# Now, we compute the same value but for each carrier
mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean1)
# carrier mean_arrival_delay
# 1: UA 3.5580111
# 2: AA 0.3642909
# 3: B6 9.4579733
# 4: DL 1.6443409
# 5: EV 15.7964311
# 6: MQ 10.7747334
# 7: US 2.1295951
# 8: WN 9.6491199
# 9: VX 1.7644644
# 10: FL 20.1159055
# 11: AS -9.9308886
# 12: 9E 7.3796692
# 13: F9 21.9207048
# 14: HA -6.9152047
# 15: YV 15.5569853
# 16: OO 11.9310345
# Now let’s compute to means in the same line of code
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean2)
# carrier mean_departure_delay mean_arrival_delay
# 1: UA 12.106073 3.5580111
# 2: AA 8.586016 0.3642909
# 3: B6 13.022522 9.4579733
# 4: DL 9.264505 1.6443409
# 5: EV 19.955390 15.7964311
# 6: MQ 10.552041 10.7747334
# 7: US 3.782418 2.1295951
# 8: WN 17.711744 9.6491199
# 9: VX 12.869421 1.7644644
# 10: FL 18.726075 20.1159055
# 11: AS 5.804775 -9.9308886
# 12: 9E 16.725769 7.3796692
# 13: F9 20.215543 21.9207048
# 14: HA 4.900585 -6.9152047
# 15: YV 18.996330 15.5569853
# 16: OO 12.586207 11.9310345
### Create a new variable called gain
# this is the difference between arrival delay and departure delay
DT[, gain:= arr_delay - dep_delay]
# Compute the median gain per carrier
median_gain = DT[, median(gain, na.rm = TRUE), by = carrier]
print(median_gain)Exploratory data analysisเป็นแนวคิดที่พัฒนาโดย John Tuckey (1977) ซึ่งประกอบด้วยมุมมองใหม่ของสถิติ ความคิดของ Tuckey คือในสถิติแบบดั้งเดิมข้อมูลไม่ได้ถูกสำรวจในรูปแบบกราฟิกเป็นเพียงการใช้เพื่อทดสอบสมมติฐาน ความพยายามครั้งแรกที่จะพัฒนาเครื่องมือที่ทำในสแตนฟอโครงการนี้ก็ถูกเรียกว่าprim9 เครื่องมือนี้สามารถแสดงภาพข้อมูลในเก้ามิติดังนั้นจึงสามารถให้มุมมองหลายตัวแปรของข้อมูลได้
ในช่วงไม่กี่วันที่ผ่านมาการวิเคราะห์ข้อมูลเชิงสำรวจเป็นสิ่งจำเป็นและรวมอยู่ในวงจรชีวิตของการวิเคราะห์ข้อมูลขนาดใหญ่ ความสามารถในการค้นหาข้อมูลเชิงลึกและสามารถสื่อสารได้อย่างมีประสิทธิภาพในองค์กรนั้นมาจากความสามารถด้าน EDA ที่แข็งแกร่ง
จากแนวคิดของ Tuckey Bell Labs ได้พัฒนาไฟล์ S programming languageเพื่อให้อินเทอร์เฟซแบบโต้ตอบสำหรับการทำสถิติ แนวคิดของ S คือการให้ความสามารถด้านกราฟิกที่ครอบคลุมด้วยภาษาที่ใช้งานง่าย ในโลกปัจจุบันในบริบทของ Big DataR ที่ขึ้นอยู่กับ S ภาษาโปรแกรมเป็นซอฟต์แวร์ยอดนิยมสำหรับการวิเคราะห์
โปรแกรมต่อไปนี้แสดงให้เห็นถึงการใช้การวิเคราะห์ข้อมูลเชิงสำรวจ
ต่อไปนี้เป็นตัวอย่างของการวิเคราะห์ข้อมูลเชิงสำรวจ รหัสนี้ยังมีอยู่ในpart1/eda/exploratory_data_analysis.R ไฟล์.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Using the code from the previous section
# This computes the mean arrival and departure delays by carrier.
DT <- as.data.table(flights)
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
# In order to plot data in R usign ggplot, it is normally needed to reshape the data
# We want to have the data in long format for plotting with ggplot
dt = melt(mean2, id.vars = ’carrier’)
# Take a look at the first rows
print(head(dt))
# Take a look at the help for ?geom_point and geom_line to find similar examples
# Here we take the carrier code as the x axis
# the value from the dt data.table goes in the y axis
# The variable column represents the color
p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +
geom_point() + # Plots points
geom_line() + # Plots lines
theme_bw() + # Uses a white background
labs(list(title = 'Mean arrival and departure delay by carrier',
x = 'Carrier', y = 'Mean delay'))
print(p)
# Save the plot to disk
ggsave('mean_delay_by_carrier.png', p,
width = 10.4, height = 5.07)รหัสควรสร้างภาพดังต่อไปนี้ -

ในการทำความเข้าใจข้อมูลมักจะมีประโยชน์ในการแสดงภาพ โดยปกติในแอปพลิเคชัน Big Data ความสนใจจะขึ้นอยู่กับการค้นหาข้อมูลเชิงลึกมากกว่าการสร้างพล็อตที่สวยงามเท่านั้น ต่อไปนี้เป็นตัวอย่างของวิธีการต่างๆในการทำความเข้าใจข้อมูลโดยใช้พล็อต
ในการเริ่มวิเคราะห์ข้อมูลเที่ยวบินเราสามารถเริ่มต้นด้วยการตรวจสอบว่ามีความสัมพันธ์ระหว่างตัวแปรตัวเลขหรือไม่ รหัสนี้ยังมีอยู่ในbda/part1/data_visualization/data_visualization.R ไฟล์.
# Install the package corrplot by running
install.packages('corrplot')
# then load the library
library(corrplot)
# Load the following libraries
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# We will continue working with the flights data
DT <- as.data.table(flights)
head(DT) # take a look
# We select the numeric variables after inspecting the first rows.
numeric_variables = c('dep_time', 'dep_delay',
'arr_time', 'arr_delay', 'air_time', 'distance')
# Select numeric variables from the DT data.table
dt_num = DT[, numeric_variables, with = FALSE]
# Compute the correlation matrix of dt_num
cor_mat = cor(dt_num, use = "complete.obs")
print(cor_mat)
### Here is the correlation matrix
# dep_time dep_delay arr_time arr_delay air_time distance
# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373
# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090
# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917
# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776
# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965
# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000
# We can display it visually to get a better understanding of the data
corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")
# save it to disk
png('corrplot.png')
print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))
dev.off()รหัสนี้สร้างการแสดงภาพเมทริกซ์สหสัมพันธ์ต่อไปนี้ -

เราจะเห็นในพล็อตว่ามีความสัมพันธ์กันอย่างมากระหว่างตัวแปรบางตัวในชุดข้อมูล ตัวอย่างเช่นความล่าช้าในการมาถึงและความล่าช้าในการออกเดินทางดูเหมือนจะมีความสัมพันธ์กันอย่างมาก เราสามารถเห็นสิ่งนี้ได้เนื่องจากวงรีแสดงความสัมพันธ์แบบเกือบจะเป็นเส้นตรงระหว่างตัวแปรทั้งสองอย่างไรก็ตามมันไม่ง่ายเลยที่จะหาสาเหตุจากผลลัพธ์นี้
เราไม่สามารถพูดได้ว่าเนื่องจากตัวแปรสองตัวมีความสัมพันธ์กันตัวแปรนั้นจึงมีผลต่ออีกตัวแปรหนึ่ง นอกจากนี้เราพบว่าในพล็อตมีความสัมพันธ์ที่แข็งแกร่งระหว่างเวลาออกอากาศและระยะทางซึ่งค่อนข้างสมเหตุสมผลที่จะคาดหวังเช่นเดียวกับระยะทางที่มากขึ้นเวลาในการบินควรเพิ่มขึ้น
นอกจากนี้เรายังสามารถทำการวิเคราะห์ข้อมูลแบบตัวแปรเดียวได้ วิธีที่ง่ายและมีประสิทธิภาพในการแสดงภาพการแจกแจงคือbox-plots. โค้ดต่อไปนี้แสดงให้เห็นถึงวิธีการสร้างบ็อกซ์พล็อตและแผนภูมิโครงตาข่ายโดยใช้ไลบรารี ggplot2 รหัสนี้ยังมีอยู่ในbda/part1/data_visualization/boxplots.R ไฟล์.
source('data_visualization.R')
### Analyzing Distributions using box-plots
# The following shows the distance as a function of the carrier
p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier
in the x axis and distance in the y axis
geom_box-plot() + # Use the box-plot geom
theme_bw() + # Leave a white background - More in line with tufte's
principles than the default
guides(fill = FALSE) + # Remove legend
labs(list(title = 'Distance as a function of carrier', # Add labels
x = 'Carrier', y = 'Distance'))
p
# Save to disk
png(‘boxplot_carrier.png’)
print(p)
dev.off()
# Let's add now another variable, the month of each flight
# We will be using facet_wrap for this
p = ggplot(DT, aes(carrier, distance, fill = carrier)) +
geom_box-plot() +
theme_bw() +
guides(fill = FALSE) +
facet_wrap(~month) + # This creates the trellis plot with the by month variable
labs(list(title = 'Distance as a function of carrier by month',
x = 'Carrier', y = 'Distance'))
p
# The plot shows there aren't clear differences between distance in different months
# Save to disk
png('boxplot_carrier_by_month.png')
print(p)
dev.off()ส่วนนี้มีไว้เพื่อแนะนำผู้ใช้ให้รู้จักกับภาษาโปรแกรม R R สามารถดาวน์โหลดได้จากเว็บไซต์ Cran สำหรับผู้ใช้ Windows จะเป็นประโยชน์ในการติดตั้ง rtoolsและrstudio IDE
แนวคิดทั่วไปที่อยู่เบื้องหลัง R คือทำหน้าที่เป็นอินเทอร์เฟซสำหรับซอฟต์แวร์อื่น ๆ ที่พัฒนาในภาษาคอมไพล์เช่น C, C ++ และ Fortran และเพื่อให้ผู้ใช้มีเครื่องมือโต้ตอบในการวิเคราะห์ข้อมูล
ไปที่โฟลเดอร์ของไฟล์ zip ของหนังสือ bda/part2/R_introduction และเปิดไฟล์ R_introduction.Rprojไฟล์. เพื่อเปิดเซสชัน RStudio จากนั้นเปิดไฟล์ 01_vectors.R เรียกใช้สคริปต์ทีละบรรทัดและทำตามความคิดเห็นในโค้ด อีกทางเลือกหนึ่งที่มีประโยชน์ในการเรียนรู้คือเพียงแค่พิมพ์โค้ดซึ่งจะช่วยให้คุณคุ้นเคยกับไวยากรณ์ R ในความคิดเห็น R จะเขียนด้วยสัญลักษณ์ #
เพื่อแสดงผลลัพธ์ของการรันโค้ด R ในหนังสือหลังจากประเมินโค้ดแล้วผลลัพธ์ R จะแสดงความคิดเห็น ด้วยวิธีนี้คุณสามารถคัดลอกและวางโค้ดในหนังสือและลองใช้ส่วนต่างๆใน R ได้โดยตรง
# Create a vector of numbers
numbers = c(1, 2, 3, 4, 5)
print(numbers)
# [1] 1 2 3 4 5
# Create a vector of letters
ltrs = c('a', 'b', 'c', 'd', 'e')
# [1] "a" "b" "c" "d" "e"
# Concatenate both
mixed_vec = c(numbers, ltrs)
print(mixed_vec)
# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"ลองวิเคราะห์สิ่งที่เกิดขึ้นในโค้ดก่อนหน้านี้ เราจะเห็นว่ามันเป็นไปได้ที่จะสร้างเวกเตอร์ด้วยตัวเลขและตัวอักษร เราไม่จำเป็นต้องบอก R ว่าเราต้องการข้อมูลประเภทใดล่วงหน้า ในที่สุดเราก็สามารถสร้างเวกเตอร์ที่มีทั้งตัวเลขและตัวอักษร เวกเตอร์ mixed_vec บังคับตัวเลขให้เป็นอักขระเราสามารถเห็นสิ่งนี้ได้โดยการแสดงภาพว่าค่าถูกพิมพ์ภายในเครื่องหมายคำพูด
รหัสต่อไปนี้แสดงชนิดข้อมูลของเวกเตอร์ที่แตกต่างกันตามที่ส่งคืนโดยคลาสฟังก์ชัน เป็นเรื่องปกติที่จะใช้ฟังก์ชันคลาสเพื่อ "ซักถาม" วัตถุโดยถามเขาว่าคลาสของเขาคืออะไร
### Evaluate the data types using class
### One dimensional objects
# Integer vector
num = 1:10
class(num)
# [1] "integer"
# Numeric vector, it has a float, 10.5
num = c(1:10, 10.5)
class(num)
# [1] "numeric"
# Character vector
ltrs = letters[1:10]
class(ltrs)
# [1] "character"
# Factor vector
fac = as.factor(ltrs)
class(fac)
# [1] "factor"R รองรับวัตถุสองมิติด้วย ในโค้ดต่อไปนี้มีตัวอย่างโครงสร้างข้อมูลที่นิยมใช้กันมากที่สุดสองแบบที่ใช้ใน R: เมทริกซ์และ data.frame
# Matrix
M = matrix(1:12, ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] 1 4 7 10
# [2,] 2 5 8 11
# [3,] 3 6 9 12
lM = matrix(letters[1:12], ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] "a" "d" "g" "j"
# [2,] "b" "e" "h" "k"
# [3,] "c" "f" "i" "l"
# Coerces the numbers to character
# cbind concatenates two matrices (or vectors) in one matrix
cbind(M, lM)
# [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
# [1,] "1" "4" "7" "10" "a" "d" "g" "j"
# [2,] "2" "5" "8" "11" "b" "e" "h" "k"
# [3,] "3" "6" "9" "12" "c" "f" "i" "l"
class(M)
# [1] "matrix"
class(lM)
# [1] "matrix"
# data.frame
# One of the main objects of R, handles different data types in the same object.
# It is possible to have numeric, character and factor vectors in the same data.frame
df = data.frame(n = 1:5, l = letters[1:5])
df
# n l
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 eดังที่แสดงในตัวอย่างก่อนหน้านี้คุณสามารถใช้ชนิดข้อมูลที่แตกต่างกันในออบเจ็กต์เดียวกันได้ โดยทั่วไปนี่คือวิธีการนำเสนอข้อมูลในฐานข้อมูลส่วน API ของข้อมูลคือข้อความหรือเวกเตอร์อักขระและตัวเลขอื่น ๆ In เป็นงานของนักวิเคราะห์ในการกำหนดประเภทข้อมูลทางสถิติที่จะกำหนดจากนั้นใช้ชนิดข้อมูล R ที่ถูกต้องสำหรับข้อมูลนั้น โดยปกติแล้วในทางสถิติเราถือว่าตัวแปรเป็นประเภทต่อไปนี้ -
- Numeric
- ระบุหรือจัดหมวดหมู่
- Ordinal
ใน R เวกเตอร์สามารถเป็นคลาสต่อไปนี้ -
- ตัวเลข - จำนวนเต็ม
- Factor
- ปัจจัยสั่งซื้อ
R จัดเตรียมชนิดข้อมูลสำหรับตัวแปรทางสถิติแต่ละประเภท อย่างไรก็ตามปัจจัยที่มีการสั่งซื้อนั้นแทบจะไม่ได้ใช้ แต่สามารถสร้างขึ้นโดยฟังก์ชันแฟกเตอร์หรือตามลำดับ
ส่วนต่อไปนี้ใช้กับแนวคิดของการจัดทำดัชนี นี่เป็นการดำเนินการที่ค่อนข้างบ่อยและเกี่ยวข้องกับปัญหาในการเลือกส่วนของวัตถุและทำการแปลง
# Let's create a data.frame
df = data.frame(numbers = 1:26, letters)
head(df)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# str gives the structure of a data.frame, it’s a good summary to inspect an object
str(df)
# 'data.frame': 26 obs. of 2 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ... # $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# The latter shows the letters character vector was coerced as a factor.
# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame
# read ?data.frame for more information
class(df)
# [1] "data.frame"
### Indexing
# Get the first row
df[1, ]
# numbers letters
# 1 1 a
# Used for programming normally - returns the output as a list
df[1, , drop = TRUE]
# $numbers # [1] 1 # # $letters
# [1] a
# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z
# Get several rows of the data.frame
df[5:7, ]
# numbers letters
# 5 5 e
# 6 6 f
# 7 7 g
### Add one column that mixes the numeric column with the factor column
df$mixed = paste(df$numbers, df$letters, sep = ’’) str(df) # 'data.frame': 26 obs. of 3 variables: # $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ... # $ mixed : chr "1a" "2b" "3c" "4d" ...
### Get columns
# Get the first column
df[, 1]
# It returns a one dimensional vector with that column
# Get two columns
df2 = df[, 1:2]
head(df2)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# Get the first and third columns
df3 = df[, c(1, 3)]
df3[1:3, ]
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
### Index columns from their names
names(df)
# [1] "numbers" "letters" "mixed"
# This is the best practice in programming, as many times indeces change, but
variable names don’t
# We create a variable with the names we want to subset
keep_vars = c("numbers", "mixed")
df4 = df[, keep_vars]
head(df4)
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
### subset rows and columns
# Keep the first five rows
df5 = df[1:5, keep_vars]
df5
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# subset rows using a logical condition
df6 = df[df$numbers < 10, keep_vars]
df6
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
# 7 7 7g
# 8 8 8h
# 9 9 9iSQL ย่อมาจากภาษาแบบสอบถามที่มีโครงสร้าง เป็นหนึ่งในภาษาที่ใช้กันอย่างแพร่หลายในการดึงข้อมูลจากฐานข้อมูลในคลังข้อมูลแบบดั้งเดิมและเทคโนโลยีข้อมูลขนาดใหญ่ เพื่อแสดงให้เห็นถึงพื้นฐานของ SQL เราจะดำเนินการกับตัวอย่าง เพื่อมุ่งเน้นไปที่ภาษาเราจะใช้ SQL ภายใน R ในแง่ของการเขียนโค้ด SQL จะเหมือนกับที่ทำในฐานข้อมูล
หลักของ SQL คือสามคำสั่ง: SELECT, FROM และ WHERE ตัวอย่างต่อไปนี้ใช้ประโยชน์จากกรณีการใช้งานที่พบบ่อยที่สุดของ SQL ไปที่โฟลเดอร์bda/part2/SQL_introduction และเปิดไฟล์ SQL_introduction.Rprojไฟล์. จากนั้นเปิดสคริปต์ 01_select.R ในการเขียนโค้ด SQL ใน R เราจำเป็นต้องติดตั้งไฟล์sqldf แพ็คเกจตามที่แสดงในรหัสต่อไปนี้
# Install the sqldf package
install.packages('sqldf')
# load the library
library('sqldf')
library(nycflights13)
# We will be working with the fligths dataset in order to introduce SQL
# Let’s take a look at the table
str(flights)
# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:
# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
# $ month : int 1 1 1 1 1 1 1 1 1 1 ... # $ day : int 1 1 1 1 1 1 1 1 1 1 ...
# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ... # $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ... # $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...
# $ carrier : chr "UA" "UA" "AA" "B6" ... # $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...
# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ... # $ origin : chr "EWR" "LGA" "JFK" "JFK" ...
# $ dest : chr "IAH" "IAH" "MIA" "BQN" ... # $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...
# $ distance : num 1400 1416 1089 1576 762 ... # $ hour : num 5 5 5 5 5 5 5 5 5 5 ...
# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...คำสั่ง select ใช้เพื่อดึงคอลัมน์จากตารางและทำการคำนวณ คำสั่ง SELECT ที่ง่ายที่สุดแสดงในรูปแบบej1. เรายังสามารถสร้างตัวแปรใหม่ดังที่แสดงในej2.
### SELECT statement
ej1 = sqldf("
SELECT
dep_time
,dep_delay
,arr_time
,carrier
,tailnum
FROM
flights
")
head(ej1)
# dep_time dep_delay arr_time carrier tailnum
# 1 517 2 830 UA N14228
# 2 533 4 850 UA N24211
# 3 542 2 923 AA N619AA
# 4 544 -1 1004 B6 N804JB
# 5 554 -6 812 DL N668DN
# 6 554 -4 740 UA N39463
# In R we can use SQL with the sqldf function. It works exactly the same as in
a database
# The data.frame (in this case flights) represents the table we are querying
and goes in the FROM statement
# We can also compute new variables in the select statement using the syntax:
# old_variables as new_variable
ej2 = sqldf("
SELECT
arr_delay - dep_delay as gain,
carrier
FROM
flights
")
ej2[1:5, ]
# gain carrier
# 1 9 UA
# 2 16 UA
# 3 31 AA
# 4 -17 B6
# 5 -19 DLหนึ่งในคุณสมบัติที่ใช้บ่อยที่สุดของ SQL คือกลุ่มตามคำสั่ง สิ่งนี้ช่วยในการคำนวณค่าตัวเลขสำหรับกลุ่มต่างๆของตัวแปรอื่น เปิดสคริปต์ 02_group_by.R
### GROUP BY
# Computing the average
ej3 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
avg(dep_delay) as mean_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# mean_arr_delay mean_dep_delay carrier
# 1 7.3796692 16.725769 9E
# 2 0.3642909 8.586016 AA
# 3 -9.9308886 5.804775 AS
# 4 9.4579733 13.022522 B6
# 5 1.6443409 9.264505 DL
# 6 15.7964311 19.955390 EV
# 7 21.9207048 20.215543 F9
# 8 20.1159055 18.726075 FL
# 9 -6.9152047 4.900585 HA
# 10 10.7747334 10.552041 MQ
# 11 11.9310345 12.586207 OO
# 12 3.5580111 12.106073 UA
# 13 2.1295951 3.782418 US
# 14 1.7644644 12.869421 VX
# 15 9.6491199 17.711744 WN
# 16 15.5569853 18.996330 YV
# Other aggregations
ej4 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
min(dep_delay) as min_dep_delay,
max(dep_delay) as max_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# We can compute the minimun, mean, and maximum values of a numeric value
ej4
# mean_arr_delay min_dep_delay max_dep_delay carrier
# 1 7.3796692 -24 747 9E
# 2 0.3642909 -24 1014 AA
# 3 -9.9308886 -21 225 AS
# 4 9.4579733 -43 502 B6
# 5 1.6443409 -33 960 DL
# 6 15.7964311 -32 548 EV
# 7 21.9207048 -27 853 F9
# 8 20.1159055 -22 602 FL
# 9 -6.9152047 -16 1301 HA
# 10 10.7747334 -26 1137 MQ
# 11 11.9310345 -14 154 OO
# 12 3.5580111 -20 483 UA
# 13 2.1295951 -19 500 US
# 14 1.7644644 -20 653 VX
# 15 9.6491199 -13 471 WN
# 16 15.5569853 -16 387 YV
### We could be also interested in knowing how many observations each carrier has
ej5 = sqldf("
SELECT
carrier, count(*) as count
FROM
flights
GROUP BY
carrier
")
ej5
# carrier count
# 1 9E 18460
# 2 AA 32729
# 3 AS 714
# 4 B6 54635
# 5 DL 48110
# 6 EV 54173
# 7 F9 685
# 8 FL 3260
# 9 HA 342
# 10 MQ 26397
# 11 OO 32
# 12 UA 58665
# 13 US 20536
# 14 VX 5162
# 15 WN 12275
# 16 YV 601คุณลักษณะที่มีประโยชน์ที่สุดของ SQL คือการรวม การรวมหมายความว่าเราต้องการรวมตาราง A และตาราง B ในตารางเดียวโดยใช้คอลัมน์เดียวเพื่อจับคู่ค่าของทั้งสองตาราง มีหลายประเภทของการรวมในทางปฏิบัติในการเริ่มต้นสิ่งเหล่านี้จะเป็นประโยชน์สูงสุด: การรวมภายในและการรวมภายนอกด้านซ้าย
# Let’s create two tables: A and B to demonstrate joins.
A = data.frame(c1 = 1:4, c2 = letters[1:4])
B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])
A
# c1 c2
# 1 a
# 2 b
# 3 c
# 4 d
B
# c1 c2
# 2 b
# 4 c
# 5 d
# 6 e
### INNER JOIN
# This means to match the observations of the column we would join the tables by.
inner = sqldf("
SELECT
A.c1, B.c2
FROM
A INNER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
inner
# c1 c2
# 2 b
# 4 c
### LEFT OUTER JOIN
# the left outer join, sometimes just called left join will return the
# first all the values of the column used from the A table
left = sqldf("
SELECT
A.c1, B.c2
FROM
A LEFT OUTER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
left
# c1 c2
# 1 <NA>
# 2 b
# 3 <NA>
# 4 cแนวทางแรกในการวิเคราะห์ข้อมูลคือการวิเคราะห์ด้วยสายตา โดยปกติวัตถุประสงค์ในการทำเช่นนี้คือการหาความสัมพันธ์ระหว่างตัวแปรและคำอธิบายที่ไม่แปรผันของตัวแปร เราสามารถแบ่งกลยุทธ์เหล่านี้เป็น -
- การวิเคราะห์แบบ Univariate
- การวิเคราะห์หลายตัวแปร
วิธีการแบบกราฟิกที่แตกต่างกัน
Univariateเป็นคำศัพท์ทางสถิติ ในทางปฏิบัติหมายความว่าเราต้องการวิเคราะห์ตัวแปรโดยเป็นอิสระจากข้อมูลที่เหลือ แผนการที่อนุญาตให้ทำได้อย่างมีประสิทธิภาพคือ -
กล่องพล็อต
โดยปกติ Box-Plots จะใช้เพื่อเปรียบเทียบการแจกแจง เป็นวิธีที่ดีในการตรวจสอบด้วยสายตาว่ามีความแตกต่างระหว่างการแจกแจงหรือไม่ เราสามารถดูได้ว่าราคาเพชรสำหรับการเจียระไนแบบต่างๆมีความแตกต่างกันหรือไม่
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)เราจะเห็นว่าในพล็อตมีความแตกต่างในการกระจายของราคาเพชรในการเจียระไนประเภทต่างๆ

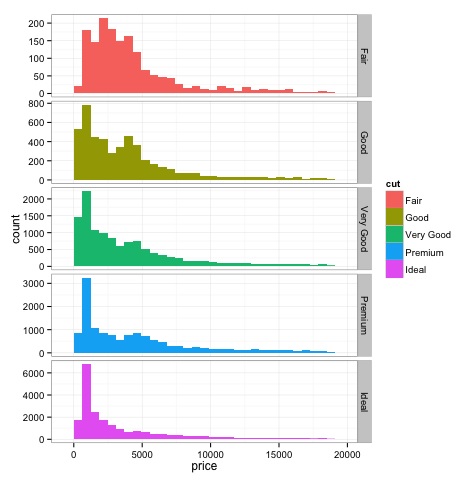
ฮิสโตแกรม
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()ผลลัพธ์ของโค้ดด้านบนจะเป็นดังนี้ -
วิธีการแบบกราฟิกหลายตัวแปร
วิธีการแบบกราฟิกหลายตัวแปรในการวิเคราะห์ข้อมูลเชิงสำรวจมีวัตถุประสงค์ในการค้นหาความสัมพันธ์ระหว่างตัวแปรต่างๆ มีสองวิธีในการทำสิ่งนี้ให้สำเร็จซึ่งมักใช้: การพล็อตเมทริกซ์สหสัมพันธ์ของตัวแปรตัวเลขหรือเพียงแค่พล็อตข้อมูลดิบเป็นเมทริกซ์ของการกระจาย
เพื่อแสดงให้เห็นถึงสิ่งนี้เราจะใช้ชุดข้อมูลเพชร หากต้องการทำตามรหัสให้เปิดสคริปต์bda/part2/charts/03_multivariate_analysis.R.
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)รหัสจะสร้างผลลัพธ์ต่อไปนี้ -

นี่คือบทสรุปมันบอกเราว่ามีความสัมพันธ์ที่แข็งแกร่งระหว่างราคาและคาเร็ตและตัวแปรอื่น ๆ ไม่มากนัก
เมทริกซ์สหสัมพันธ์จะมีประโยชน์เมื่อเรามีตัวแปรจำนวนมากซึ่งในกรณีนี้การพล็อตข้อมูลดิบจะไม่สามารถใช้งานได้จริง ดังที่ได้กล่าวมาแล้วคุณสามารถแสดงข้อมูลดิบได้ด้วย -
library(GGally)
ggpairs(df)เราสามารถเห็นได้ในพล็อตว่าผลลัพธ์ที่แสดงในแผนที่ความร้อนได้รับการยืนยันมีความสัมพันธ์ 0.922 ระหว่างตัวแปรราคาและกะรัต
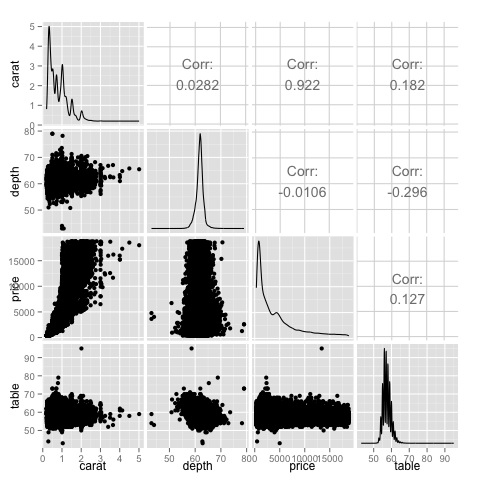
เป็นไปได้ที่จะเห็นภาพความสัมพันธ์นี้ในตารางราคากะรัตที่อยู่ในดัชนี (3, 1) ของเมทริกซ์ scatterplot
มีเครื่องมือมากมายที่ช่วยให้นักวิทยาศาสตร์ข้อมูลสามารถวิเคราะห์ข้อมูลได้อย่างมีประสิทธิภาพ โดยปกติด้านวิศวกรรมของการวิเคราะห์ข้อมูลมุ่งเน้นไปที่ฐานข้อมูลนักวิทยาศาสตร์ข้อมูลมุ่งเน้นไปที่เครื่องมือที่สามารถใช้ผลิตภัณฑ์ข้อมูลได้ ส่วนต่อไปนี้จะกล่าวถึงข้อดีของเครื่องมือต่างๆโดยเน้นที่แพ็คเกจทางสถิติที่นักวิทยาศาสตร์ข้อมูลใช้ในทางปฏิบัติบ่อยที่สุด
ภาษาการเขียนโปรแกรม R
R เป็นภาษาโปรแกรมโอเพ่นซอร์สโดยเน้นที่การวิเคราะห์ทางสถิติ สามารถแข่งขันกับเครื่องมือทางการค้าเช่น SAS, SPSS ในแง่ของความสามารถทางสถิติ คิดว่าเป็นส่วนต่อประสานกับภาษาโปรแกรมอื่น ๆ เช่น C, C ++ หรือ Fortran
ข้อดีอีกอย่างของ R คือไลบรารีโอเพ่นซอร์สจำนวนมากที่พร้อมใช้งาน ใน CRAN มีแพ็คเกจมากกว่า 6000 รายการที่สามารถดาวน์โหลดได้ฟรีและในGithub มีแพ็คเกจ R ให้เลือกมากมาย
ในแง่ของประสิทธิภาพ R นั้นช้าสำหรับการดำเนินการที่เข้มข้นเนื่องจากมีไลบรารีจำนวนมากที่มีอยู่ส่วนช้าของโค้ดจะถูกเขียนด้วยภาษาที่คอมไพล์ แต่ถ้าคุณตั้งใจจะดำเนินการที่ต้องเขียนลึกสำหรับลูป R ก็คงไม่ใช่ทางเลือกที่ดีที่สุดของคุณ เพื่อวัตถุประสงค์ในการวิเคราะห์ข้อมูลมีไลบรารีที่ดีเช่นdata.table, glmnet, ranger, xgboost, ggplot2, caret ที่อนุญาตให้ใช้ R เป็นอินเทอร์เฟซสำหรับภาษาโปรแกรมที่เร็วขึ้น
Python สำหรับการวิเคราะห์ข้อมูล
Python เป็นภาษาโปรแกรมสำหรับวัตถุประสงค์ทั่วไปและมีไลบรารีจำนวนมากที่อุทิศให้กับการวิเคราะห์ข้อมูลเช่น pandas, scikit-learn, theano, numpy และ scipy.
สิ่งที่มีอยู่ใน R ส่วนใหญ่สามารถทำได้ใน Python แต่เราพบว่า R นั้นใช้งานง่ายกว่า ในกรณีที่คุณกำลังทำงานกับชุดข้อมูลขนาดใหญ่โดยปกติ Python เป็นตัวเลือกที่ดีกว่า R Python สามารถใช้งานได้อย่างมีประสิทธิภาพในการล้างข้อมูลและประมวลผลข้อมูลทีละบรรทัด สิ่งนี้เป็นไปได้จาก R แต่ไม่ได้มีประสิทธิภาพเท่ากับ Python สำหรับงานสคริปต์
สำหรับการเรียนรู้ของเครื่อง scikit-learnเป็นสภาพแวดล้อมที่ดีที่มีอัลกอริทึมจำนวนมากที่สามารถจัดการกับชุดข้อมูลขนาดกลางได้โดยไม่มีปัญหา เมื่อเทียบกับห้องสมุดเทียบเท่าของ R (คาเร็ต)scikit-learn มี API ที่สะอาดและสอดคล้องกันมากขึ้น
จูเลีย
Julia เป็นภาษาโปรแกรมไดนามิกระดับสูงที่มีประสิทธิภาพสูงสำหรับการคำนวณทางเทคนิค ไวยากรณ์ของมันค่อนข้างคล้ายกับ R หรือ Python ดังนั้นหากคุณกำลังทำงานกับ R หรือ Python อยู่แล้วก็ควรจะเขียนโค้ดเดียวกันใน Julia ได้ค่อนข้างง่าย ภาษาค่อนข้างใหม่และเติบโตขึ้นอย่างมากในช่วงหลายปีที่ผ่านมาดังนั้นจึงเป็นทางเลือกหนึ่งในขณะนี้
เราขอแนะนำ Julia สำหรับอัลกอริทึมการสร้างต้นแบบที่มีการคำนวณอย่างเข้มข้นเช่นเครือข่ายประสาทเทียม เป็นเครื่องมือที่ดีสำหรับการวิจัย ในแง่ของการนำแบบจำลองไปใช้ในการผลิต Python อาจมีทางเลือกอื่นที่ดีกว่า อย่างไรก็ตามสิ่งนี้กลายเป็นปัญหาน้อยลงเนื่องจากมีบริการเว็บที่ทำวิศวกรรมการใช้โมเดลใน R, Python และ Julia
SAS
SAS เป็นภาษาทางการค้าที่ยังคงใช้สำหรับระบบธุรกิจอัจฉริยะ มีภาษาพื้นฐานที่ช่วยให้ผู้ใช้สามารถตั้งโปรแกรมแอพพลิเคชั่นได้หลากหลาย มีผลิตภัณฑ์เชิงพาณิชย์ค่อนข้างน้อยที่ให้ผู้ใช้ที่ไม่ใช่ผู้เชี่ยวชาญสามารถใช้เครื่องมือที่ซับซ้อนเช่นไลบรารีเครือข่ายประสาทโดยไม่จำเป็นต้องเขียนโปรแกรม
นอกเหนือจากข้อเสียที่ชัดเจนของเครื่องมือทางการค้าแล้ว SAS ยังปรับขนาดชุดข้อมูลขนาดใหญ่ได้ไม่ดี แม้แต่ชุดข้อมูลขนาดกลางก็มีปัญหากับ SAS และทำให้เซิร์ฟเวอร์ล่มได้ เฉพาะในกรณีที่คุณกำลังทำงานกับชุดข้อมูลขนาดเล็กและผู้ใช้ไม่ใช่นักวิทยาศาสตร์ข้อมูลผู้เชี่ยวชาญขอแนะนำให้ใช้ SAS สำหรับผู้ใช้ขั้นสูง R และ Python มีสภาพแวดล้อมที่มีประสิทธิผลมากขึ้น
SPSS
SPSS ปัจจุบันเป็นผลิตภัณฑ์ของ IBM สำหรับการวิเคราะห์ทางสถิติ ส่วนใหญ่จะใช้ในการวิเคราะห์ข้อมูลการสำรวจและสำหรับผู้ใช้ที่ไม่สามารถเขียนโปรแกรมได้ก็เป็นทางเลือกที่ดี มันอาจจะใช้งานง่ายเหมือน SAS แต่ในแง่ของการนำโมเดลไปใช้มันจะง่ายกว่าเนื่องจากมีโค้ด SQL เพื่อให้คะแนนโมเดล โดยปกติรหัสนี้ไม่มีประสิทธิภาพ แต่เป็นการเริ่มต้นในขณะที่ SAS ขายผลิตภัณฑ์ที่ให้คะแนนแบบจำลองสำหรับแต่ละฐานข้อมูลแยกกัน สำหรับข้อมูลขนาดเล็กและทีมที่ไม่มีประสบการณ์ SPSS เป็นตัวเลือกที่ดีพอ ๆ กับ SAS
อย่างไรก็ตามซอฟต์แวร์มีข้อ จำกัด ค่อนข้างมากและผู้ใช้ที่มีประสบการณ์จะได้รับคำสั่งจากขนาดที่มีประสิทธิผลมากขึ้นโดยใช้ R หรือ Python
Matlab, Octave
มีเครื่องมืออื่น ๆ เช่น Matlab หรือเวอร์ชันโอเพนซอร์ส (Octave) เครื่องมือเหล่านี้ส่วนใหญ่ใช้เพื่อการวิจัย ในแง่ของความสามารถ R หรือ Python สามารถทำได้ทั้งหมดที่มีอยู่ใน Matlab หรือ Octave ควรซื้อใบอนุญาตของผลิตภัณฑ์หากคุณสนใจในการสนับสนุนที่มีให้เท่านั้น
เมื่อวิเคราะห์ข้อมูลจะเป็นไปได้ที่จะมีแนวทางทางสถิติ เครื่องมือพื้นฐานที่จำเป็นในการวิเคราะห์ขั้นพื้นฐาน ได้แก่ -
- การวิเคราะห์สหสัมพันธ์
- การวิเคราะห์ความแปรปรวน
- การทดสอบสมมติฐาน
เมื่อทำงานกับชุดข้อมูลขนาดใหญ่จะไม่เกี่ยวข้องกับปัญหาเนื่องจากวิธีการเหล่านี้ไม่ได้ใช้การคำนวณอย่างเข้มข้นยกเว้นการวิเคราะห์สหสัมพันธ์ ในกรณีนี้คุณสามารถเก็บตัวอย่างได้เสมอและผลลัพธ์ควรมีประสิทธิภาพ
การวิเคราะห์สหสัมพันธ์
การวิเคราะห์สหสัมพันธ์พยายามค้นหาความสัมพันธ์เชิงเส้นระหว่างตัวแปรตัวเลข สิ่งนี้สามารถใช้ได้ในสถานการณ์ที่แตกต่างกัน การใช้งานทั่วไปอย่างหนึ่งคือการวิเคราะห์ข้อมูลเชิงสำรวจในส่วนที่ 16.0.2 ของหนังสือมีตัวอย่างพื้นฐานของแนวทางนี้ ก่อนอื่นเมตริกสหสัมพันธ์ที่ใช้ในตัวอย่างที่กล่าวถึงจะขึ้นอยู่กับPearson coefficient. อย่างไรก็ตามมีตัวชี้วัดความสัมพันธ์ที่น่าสนใจอีกตัวหนึ่งที่ไม่ได้รับผลกระทบจากค่าผิดปกติ เมตริกนี้เรียกว่าสหสัมพันธ์สเปียร์แมน
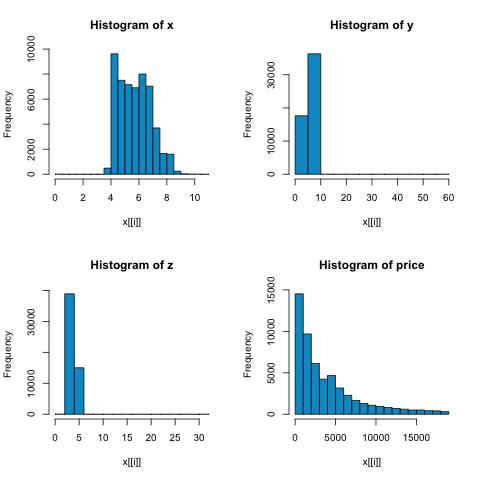
spearman correlation เมตริกมีความแข็งแกร่งมากกว่าเมื่อมีค่าผิดปกติมากกว่าวิธีของเพียร์สันและให้ค่าประมาณของความสัมพันธ์เชิงเส้นระหว่างตัวแปรตัวเลขได้ดีขึ้นเมื่อข้อมูลไม่กระจายตามปกติ
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))จากฮิสโตแกรมในรูปต่อไปนี้เราสามารถคาดหวังความแตกต่างในความสัมพันธ์ของเมตริกทั้งสอง ในกรณีนี้เนื่องจากตัวแปรไม่ได้กระจายตามปกติอย่างชัดเจนความสัมพันธ์ของสเปียร์แมนจึงเป็นการประมาณความสัมพันธ์เชิงเส้นระหว่างตัวแปรตัวเลขได้ดีกว่า
ในการคำนวณความสัมพันธ์ใน R ให้เปิดไฟล์ bda/part2/statistical_methods/correlation/correlation.R ที่มีส่วนรหัสนี้
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000การทดสอบไคสแควร์
การทดสอบไคสแควร์ช่วยให้เราทดสอบว่าตัวแปรสุ่มสองตัวเป็นอิสระหรือไม่ ซึ่งหมายความว่าการแจกแจงความน่าจะเป็นของแต่ละตัวแปรจะไม่มีผลต่อตัวแปรอื่น ในการประเมินการทดสอบใน R เราต้องสร้างตารางฉุกเฉินก่อนจากนั้นจึงส่งตารางไปที่chisq.test R ฟังก์ชัน
ตัวอย่างเช่นลองตรวจสอบว่ามีความสัมพันธ์ระหว่างตัวแปร: การเจียระไนและสีจากชุดข้อมูลของเพชรหรือไม่ การทดสอบถูกกำหนดอย่างเป็นทางการว่า -
- H0: การเจียระไนแบบแปรผันและเพชรเป็นอิสระ
- H1: การเจียระไนแบบแปรผันและเพชรไม่เป็นอิสระ
เราจะถือว่ามีความสัมพันธ์ระหว่างตัวแปรทั้งสองตามชื่อของพวกมัน แต่การทดสอบสามารถให้ "กฎ" ที่เป็นวัตถุประสงค์เพื่อบอกว่าผลลัพธ์นี้มีความสำคัญเพียงใดหรือไม่
ในข้อมูลโค้ดต่อไปนี้เราพบว่า p-value ของการทดสอบคือ 2.2e-16 ซึ่งแทบจะเป็นศูนย์ในทางปฏิบัติ จากนั้นหลังจากทำการทดสอบโดยทำMonte Carlo simulationเราพบว่าค่า p เท่ากับ 0.0004998 ซึ่งยังค่อนข้างต่ำกว่าเกณฑ์ 0.05 ผลลัพธ์นี้หมายความว่าเราปฏิเสธสมมติฐานว่าง (H0) ดังนั้นเราจึงเชื่อตัวแปรcut และ color ไม่เป็นอิสระ
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998การทดสอบ T
ความคิดของ t-testคือการประเมินว่ามีความแตกต่างในการแจกแจงตัวแปรตัวเลข # ระหว่างกลุ่มต่างๆของตัวแปรเล็กน้อยหรือไม่ เพื่อแสดงให้เห็นถึงสิ่งนี้ฉันจะเลือกระดับของระดับยุติธรรมและระดับอุดมคติของการตัดตัวแปรแฟคเตอร์จากนั้นเราจะเปรียบเทียบค่าตัวแปรตัวเลขระหว่างสองกลุ่มนั้น
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542การทดสอบ t ถูกนำไปใช้ใน R พร้อมกับ t.testฟังก์ชัน อินเทอร์เฟซของสูตรกับ t.test เป็นวิธีที่ง่ายที่สุดในการใช้แนวคิดก็คือตัวแปรตัวเลขจะถูกอธิบายโดยตัวแปรกลุ่ม
ตัวอย่างเช่น: t.test(numeric_variable ~ group_variable, data = data). ในตัวอย่างก่อนหน้านี้ไฟล์numeric_variable คือ price และ group_variable คือ cut.
จากมุมมองทางสถิติเรากำลังทดสอบว่าการแจกแจงของตัวแปรตัวเลขระหว่างสองกลุ่มมีความแตกต่างกันหรือไม่ โดยปกติการทดสอบสมมติฐานจะอธิบายด้วยสมมติฐานว่าง (H0) และสมมติฐานทางเลือก (H1)
H0: ไม่มีความแตกต่างในการกระจายของตัวแปรราคาระหว่างกลุ่มยุติธรรมและอุดมคติ
H1 มีความแตกต่างในการกระจายของตัวแปรราคาระหว่างกลุ่มยุติธรรมและอุดมคติ
สิ่งต่อไปนี้สามารถนำไปใช้ใน R ด้วยรหัสต่อไปนี้ -
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')เราสามารถวิเคราะห์ผลการทดสอบโดยตรวจสอบว่าค่า p ต่ำกว่า 0.05 หรือไม่ หากเป็นกรณีนี้เราจะคงสมมติฐานทางเลือกไว้ ซึ่งหมายความว่าเราพบความแตกต่างของราคาในสองระดับของปัจจัยตัด ตามชื่อของระดับที่เราคาดหวังผลลัพธ์นี้ แต่เราไม่คาดคิดมาก่อนว่าราคาเฉลี่ยในกลุ่ม Fail จะสูงกว่าในกลุ่ม Ideal เราสามารถเห็นสิ่งนี้ได้โดยการเปรียบเทียบค่าเฉลี่ยของแต่ละปัจจัย
plotคำสั่งสร้างกราฟที่แสดงความสัมพันธ์ระหว่างราคาและตัวแปรตัด มันเป็นกล่องพล็อต เราได้กล่าวถึงพล็อตนี้ในหัวข้อ 16.0.1 แต่โดยทั่วไปแล้วจะแสดงการกระจายของตัวแปรราคาสำหรับการตัดสองระดับที่เรากำลังวิเคราะห์
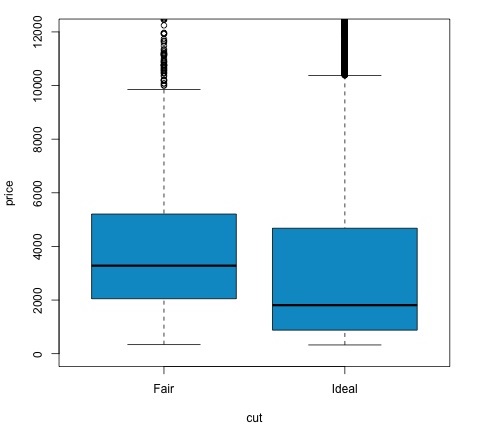
การวิเคราะห์ความแปรปรวน
การวิเคราะห์ความแปรปรวน (ANOVA) เป็นแบบจำลองทางสถิติที่ใช้ในการวิเคราะห์ความแตกต่างระหว่างการแจกแจงแบบกลุ่มโดยการเปรียบเทียบค่าเฉลี่ยและความแปรปรวนของแต่ละกลุ่มแบบจำลองนี้ได้รับการพัฒนาโดย Ronald Fisher ANOVA จัดให้มีการทดสอบทางสถิติว่าค่าเฉลี่ยของกลุ่มต่างๆมีค่าเท่ากันหรือไม่ดังนั้นจึงสรุปผลการทดสอบทีให้มากกว่าสองกลุ่ม
ANOVA มีประโยชน์ในการเปรียบเทียบกลุ่มสามกลุ่มขึ้นไปอย่างมีนัยสำคัญทางสถิติเนื่องจากการทำการทดสอบ t สองตัวอย่างหลายตัวอย่างจะส่งผลให้มีโอกาสเพิ่มขึ้นในการทำข้อผิดพลาดทางสถิติประเภท I
ในแง่ของการให้คำอธิบายทางคณิตศาสตร์จำเป็นต้องมีสิ่งต่อไปนี้เพื่อทำความเข้าใจการทดสอบ
x ij = x + (x i - x) + (x ij - x)
สิ่งนี้นำไปสู่รูปแบบต่อไปนี้ -
x ij = μ + α i + ∈ ij
โดยที่μคือค่าเฉลี่ยแกรนด์และα iคือค่าเฉลี่ยกลุ่มที่μ เงื่อนไขข้อผิดพลาด∈ ijถือว่าเป็น iid จากการแจกแจงปกติ สมมติฐานว่างของการทดสอบคือ -
α 1 = α 2 = … = α k
ในแง่ของการคำนวณสถิติการทดสอบเราต้องคำนวณสองค่า -
- ผลรวมของกำลังสองระหว่างความแตกต่างของกลุ่ม -
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- ผลรวมของกำลังสองภายในกลุ่ม
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^2$$
โดยที่ SSD Bมีระดับอิสระ k − 1 และ SSD Wมีระดับอิสระเท่ากับ N − k จากนั้นเราสามารถกำหนดความแตกต่างของค่าเฉลี่ยกำลังสองสำหรับแต่ละเมตริก
MS B = SSD B / (k - 1)
MS w = SSD w / (N - k)
สุดท้ายสถิติการทดสอบใน ANOVA ถูกกำหนดให้เป็นอัตราส่วนของสองปริมาณข้างต้น
F = MS B / MS W
ซึ่งตามด้วยการแจกแจงแบบ F โดยมีองศาอิสระk − 1และN − k ถ้าสมมุติฐานว่างเป็นจริง F น่าจะใกล้เคียงกับ 1 มิฉะนั้นค่าเฉลี่ยระหว่างกลุ่ม MSB จะมีขนาดใหญ่ซึ่งส่งผลให้ค่า F มีค่ามาก
โดยทั่วไป ANOVA จะตรวจสอบแหล่งที่มาของความแปรปรวนทั้งหมดและดูว่าส่วนใดมีส่วนทำให้มากกว่า ด้วยเหตุนี้จึงเรียกว่าการวิเคราะห์ความแปรปรวนแม้ว่าเจตนาจะเปรียบเทียบค่าเฉลี่ยกลุ่มก็ตาม
ในแง่ของการคำนวณทางสถิตินั้นค่อนข้างง่ายที่จะทำใน R ตัวอย่างต่อไปนี้จะแสดงให้เห็นถึงวิธีการทำและพล็อตผลลัพธ์
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')รหัสจะสร้างผลลัพธ์ต่อไปนี้ -

p-value ที่เราได้รับในตัวอย่างมีค่าน้อยกว่า 0.05 อย่างมีนัยสำคัญดังนั้น R จึงส่งคืนสัญลักษณ์ '***' เพื่อแสดงถึงสิ่งนี้ หมายความว่าเราปฏิเสธสมมติฐานว่างและเราพบความแตกต่างระหว่างค่า mpg ในกลุ่มต่างๆของcyl ตัวแปร.
แมชชีนเลิร์นนิงเป็นสาขาย่อยของวิทยาการคอมพิวเตอร์ที่เกี่ยวข้องกับงานต่างๆเช่นการจดจำรูปแบบการมองเห็นของคอมพิวเตอร์การรู้จำเสียงการวิเคราะห์ข้อความและมีการเชื่อมโยงที่ชัดเจนกับสถิติและการเพิ่มประสิทธิภาพทางคณิตศาสตร์ แอปพลิเคชันรวมถึงการพัฒนาเครื่องมือค้นหาการกรองสแปมการจดจำอักขระด้วยแสง (OCR) เป็นต้น ขอบเขตระหว่างการขุดข้อมูลการจดจำรูปแบบและสาขาการเรียนรู้ทางสถิตินั้นไม่ชัดเจนและโดยพื้นฐานแล้วทั้งหมดอ้างถึงปัญหาที่คล้ายกัน
การเรียนรู้ของเครื่องสามารถแบ่งออกเป็นสองประเภทของงาน -
- การเรียนรู้ภายใต้การดูแล
- การเรียนรู้ที่ไม่มีการดูแล
การเรียนรู้ภายใต้การดูแล
การเรียนรู้ภายใต้การดูแลหมายถึงประเภทของปัญหาที่มีการป้อนข้อมูลกำหนดเป็นเมทริกซ์XและเรามีความสนใจในการทำนายการตอบสนองY ที่ไหนX = {x 1 , x 2 , ... , x n }มีnพยากรณ์และมีสองค่าการ y = {C 1ค2 }
ตัวอย่างแอปพลิเคชันคือการทำนายความเป็นไปได้ที่ผู้ใช้เว็บจะคลิกโฆษณาโดยใช้คุณลักษณะทางประชากรเป็นตัวทำนาย ซึ่งมักเรียกว่าเพื่อทำนายอัตราการคลิกผ่าน (CTR) จากนั้นy = {click, don't - click}และตัวทำนายอาจเป็นที่อยู่ IP ที่ใช้, วันที่เขาเข้าสู่ไซต์, เมืองของผู้ใช้, ประเทศท่ามกลางคุณสมบัติอื่น ๆ ที่สามารถใช้ได้
การเรียนรู้ที่ไม่มีการดูแล
การเรียนรู้ที่ไม่มีผู้ดูแลเกี่ยวข้องกับปัญหาในการค้นหากลุ่มที่มีความคล้ายคลึงกันโดยไม่ต้องมีชั้นเรียนให้เรียนรู้ มีหลายวิธีในการเรียนรู้การทำแผนที่จากตัวทำนายไปจนถึงการค้นหากลุ่มที่แชร์อินสแตนซ์ที่คล้ายกันในแต่ละกลุ่มและแตกต่างกัน
การประยุกต์ใช้ตัวอย่างของการเรียนรู้ที่ไม่มีผู้ดูแลคือการแบ่งกลุ่มลูกค้า ตัวอย่างเช่นในอุตสาหกรรมโทรคมนาคมงานทั่วไปคือการแบ่งกลุ่มผู้ใช้ตามการใช้งานที่ให้กับโทรศัพท์ ซึ่งจะช่วยให้ฝ่ายการตลาดกำหนดเป้าหมายแต่ละกลุ่มด้วยผลิตภัณฑ์ที่แตกต่างกัน
Naive Bayes เป็นเทคนิคที่น่าจะเป็นในการสร้างลักษณนาม สมมติฐานลักษณะเฉพาะของลักษณนามเบย์ไร้เดียงสาคือการพิจารณาว่าค่าของคุณลักษณะเฉพาะไม่ขึ้นอยู่กับค่าของคุณลักษณะอื่นใดโดยพิจารณาจากตัวแปรคลาส
แม้จะมีสมมติฐานที่เข้าใจง่ายมากเกินไปที่กล่าวไว้ก่อนหน้านี้ แต่ลักษณนาม Bayes ที่ไร้เดียงสาก็มีผลลัพธ์ที่ดีในสถานการณ์จริงที่ซับซ้อน ข้อได้เปรียบของ naive Bayes คือต้องใช้ข้อมูลการฝึกอบรมเพียงเล็กน้อยในการประมาณค่าพารามิเตอร์ที่จำเป็นสำหรับการจำแนกประเภทและสามารถฝึกลักษณนามได้ทีละน้อย
Naive Bayes เป็นแบบจำลองความน่าจะเป็นแบบมีเงื่อนไข: กำหนดให้อินสแตนซ์ปัญหาถูกจัดประเภทโดยแสดงด้วยเวกเตอร์ x= (x 1 , …, x n ) แทนคุณสมบัติ n บางอย่าง (ตัวแปรอิสระ) ซึ่งกำหนดให้กับความน่าจะเป็นของอินสแตนซ์นี้สำหรับผลลัพธ์หรือคลาสที่เป็นไปได้ของ K
$$p(C_k|x_1,....., x_n)$$
ปัญหาเกี่ยวกับการกำหนดรูปแบบข้างต้นคือถ้าจำนวนคุณลักษณะ n มีขนาดใหญ่หรือหากคุณลักษณะสามารถรับค่าได้เป็นจำนวนมากการพิจารณาจากแบบจำลองดังกล่าวบนตารางความน่าจะเป็นจะเป็นไปไม่ได้ เราจึงปรับรูปแบบใหม่เพื่อให้ง่ายขึ้น การใช้ทฤษฎีบทของเบย์ความน่าจะเป็นแบบมีเงื่อนไขสามารถถูกย่อยสลายเป็น -
$$p(C_k|x) = \frac{p(C_k)p(x|C_k)}{p(x)}$$
ซึ่งหมายความว่าภายใต้สมมติฐานความเป็นอิสระข้างต้นการแจกแจงแบบมีเงื่อนไขเหนือตัวแปรคลาส C คือ -
$$p(C_k|x_1,....., x_n)\: = \: \frac{1}{Z}p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
โดยที่หลักฐาน Z = p (x) เป็นปัจจัยการปรับขนาดขึ้นอยู่กับ x 1 , …, x nเท่านั้นซึ่งเป็นค่าคงที่หากทราบค่าของตัวแปรคุณลักษณะ กฎทั่วไปข้อหนึ่งคือการเลือกสมมติฐานที่น่าจะเป็นไปได้มากที่สุด สิ่งนี้เรียกว่ากฎการตัดสินใจหลังหรือแผนที่สูงสุด ลักษณนามที่สอดคล้องกันซึ่งเป็นลักษณนามแบบเบย์คือฟังก์ชันที่กำหนดเลเบลคลาส$\hat{y} = C_k$ สำหรับ k ดังต่อไปนี้ -
$$\hat{y} = argmax\: p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
การใช้อัลกอริทึมใน R เป็นกระบวนการที่ตรงไปตรงมา ตัวอย่างต่อไปนี้แสดงให้เห็นถึงวิธีฝึกตัวแยกประเภท Naive Bayes และใช้สำหรับการคาดคะเนในปัญหาการกรองจดหมายขยะ
สคริปต์ต่อไปนี้มีอยู่ในไฟล์ bda/part3/naive_bayes/naive_bayes.R ไฟล์.
# Install these packages
pkgs = c("klaR", "caret", "ElemStatLearn")
install.packages(pkgs)
library('ElemStatLearn')
library("klaR")
library("caret")
# Split the data in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.9))
train = spam[inx,]
test = spam[-inx,]
# Define a matrix with features, X_train
# And a vector with class labels, y_train
X_train = train[,-58]
y_train = train$spam X_test = test[,-58] y_test = test$spam
# Train the model
nb_model = train(X_train, y_train, method = 'nb',
trControl = trainControl(method = 'cv', number = 3))
# Compute
preds = predict(nb_model$finalModel, X_test)$class
tbl = table(y_test, yhat = preds)
sum(diag(tbl)) / sum(tbl)
# 0.7217391ดังที่เราเห็นจากผลลัพธ์ความแม่นยำของแบบจำลอง Naive Bayes คือ 72% ซึ่งหมายความว่าโมเดลจำแนก 72% ของอินสแตนซ์ได้อย่างถูกต้อง
k-mean clustering มีจุดมุ่งหมายเพื่อแบ่งพาร์ติชัน n การสังเกตเป็น k clusters ซึ่งการสังเกตแต่ละครั้งเป็นของคลัสเตอร์ที่มีค่าเฉลี่ยใกล้เคียงที่สุดซึ่งทำหน้าที่เป็นต้นแบบของคลัสเตอร์ ส่งผลให้เกิดการแบ่งพื้นที่ข้อมูลลงในเซลล์ Voronoi
ด้วยชุดการสังเกต(x 1 , x 2 , …, x n )โดยที่การสังเกตแต่ละครั้งเป็นเวกเตอร์จริง d มิติการจัดกลุ่ม k-mean มีจุดมุ่งหมายเพื่อแบ่งการสังเกต n ออกเป็น k กลุ่มG = {G 1 , G 2 , …, G k }เพื่อลดผลรวมภายในคลัสเตอร์ของกำลังสอง (WCSS) ที่กำหนดไว้ดังนี้ -
$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x - \mu_{i}\parallel ^2$$
สูตรต่อมาแสดงฟังก์ชันวัตถุประสงค์ที่ย่อเล็กสุดเพื่อค้นหาต้นแบบที่เหมาะสมที่สุดในการทำคลัสเตอร์ k-mean สัญชาตญาณของสูตรคือเราต้องการค้นหากลุ่มที่แตกต่างกันและสมาชิกแต่ละคนของแต่ละกลุ่มควรมีความคล้ายคลึงกับสมาชิกอื่น ๆ ของแต่ละคลัสเตอร์
ตัวอย่างต่อไปนี้สาธิตวิธีการรันอัลกอริทึมการทำคลัสเตอร์ k-mean ใน R
library(ggplot2)
# Prepare Data
data = mtcars
# We need to scale the data to have zero mean and unit variance
data <- scale(data)
# Determine number of clusters
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:dim(data)[2]) {
wss[i] <- sum(kmeans(data, centers = i)$withinss)
}
# Plot the clusters
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters",
ylab = "Within groups sum of squares")เพื่อหาค่า K ที่ดีเราสามารถพล็อตผลรวมภายในกลุ่มของกำลังสองสำหรับค่าต่าง ๆ ของ K โดยปกติแล้วเมตริกนี้จะลดลงเมื่อมีการเพิ่มกลุ่มมากขึ้นเราต้องการหาจุดที่การลดลงของผลรวมภายในกลุ่ม ของกำลังสองเริ่มลดลงอย่างช้าๆ ในพล็อตค่านี้แสดงได้ดีที่สุดด้วย K = 6

เมื่อกำหนดค่าของ K แล้วจำเป็นต้องเรียกใช้อัลกอริทึมด้วยค่านั้น
# K-Means Cluster Analysis
fit <- kmeans(data, 5) # 5 cluster solution
# get cluster means
aggregate(data,by = list(fit$cluster),FUN = mean)
# append cluster assignment
data <- data.frame(data, fit$cluster)ให้ฉัน = ฉัน1ฉัน2 , ... , ฉันnเป็นชุดของ n คุณลักษณะไบนารีที่เรียกว่ารายการ ให้D = t 1 , t 2 , ... , t mเป็นชุดของธุรกรรมที่เรียกว่าฐานข้อมูล แต่ละธุรกรรมใน D มีรหัสธุรกรรมที่ไม่ซ้ำกันและมีชุดย่อยของรายการใน I กฎถูกกำหนดให้เป็นนัยของรูปแบบ X ⇒ Y โดยที่ X, Y ⊆ I และ X ∩ Y = ∅
ชุดของรายการ (สำหรับชุดรายการแบบสั้น) X และ Y เรียกว่าก่อนหน้า (ด้านซ้ายมือหรือ LHS) และผลที่ตามมา (ด้านขวามือหรือ RHS) ของกฎ
เพื่อแสดงแนวคิดเราใช้ตัวอย่างเล็ก ๆ จากโดเมนซูเปอร์มาร์เก็ต ชุดรายการคือ I = {นมขนมปังเนยเบียร์} และฐานข้อมูลขนาดเล็กที่มีรายการดังแสดงในตารางต่อไปนี้
| รหัสธุรกรรม | รายการ |
|---|---|
| 1 | นมขนมปัง |
| 2 | ขนมปังเนย |
| 3 | เบียร์ |
| 4 | นมขนมปังเนย |
| 5 | ขนมปังเนย |
ตัวอย่างกฎสำหรับซูเปอร์มาร์เก็ตอาจเป็น {นมขนมปัง} ⇒ {เนย} ซึ่งหมายความว่าหากซื้อนมและขนมปังลูกค้าก็ซื้อเนยเช่นกัน ในการเลือกกฎที่น่าสนใจจากชุดของกฎที่เป็นไปได้ทั้งหมดสามารถใช้ข้อ จำกัด เกี่ยวกับการวัดความสำคัญและความสนใจต่างๆได้ ข้อ จำกัด ที่รู้จักกันดีคือเกณฑ์ขั้นต่ำในการสนับสนุนและความมั่นใจ
การสนับสนุนการสนับสนุน (X) ของชุดรายการ X ถูกกำหนดเป็นสัดส่วนของธุรกรรมในชุดข้อมูลซึ่งมีชุดรายการ ในฐานข้อมูลตัวอย่างในตารางที่ 1 ชุดรายการ {milk, bread} รองรับ 2/5 = 0.4 เนื่องจากเกิดขึ้นใน 40% ของธุรกรรมทั้งหมด (2 จาก 5 ธุรกรรม) การค้นหาชุดรายการที่ใช้บ่อยสามารถมองได้ว่าเป็นการทำให้ปัญหาการเรียนรู้ที่ไม่ได้รับการดูแลง่ายขึ้น
ความเชื่อมั่นของกฎถูกกำหนด conf (X ⇒ Y) = supp (X ∪ Y) / supp (X) ตัวอย่างเช่นกฎ {milk, bread} ⇒ {butter} มีค่าความเชื่อมั่น 0.2 / 0.4 = 0.5 ในฐานข้อมูลในตารางที่ 1 ซึ่งหมายความว่า 50% ของธุรกรรมที่มีนมและขนมปังนั้นถูกต้อง ความเชื่อมั่นสามารถตีความได้ว่าเป็นค่าประมาณของความน่าจะเป็น P (Y | X) ความน่าจะเป็นในการค้นหา RHS ของกฎในธุรกรรมภายใต้เงื่อนไขที่ธุรกรรมเหล่านี้มี LHS ด้วย
ในสคริปต์ที่อยู่ใน bda/part3/apriori.R รหัสที่จะใช้ apriori algorithm สามารถพบได้
# Load the library for doing association rules
# install.packages(’arules’)
library(arules)
# Data preprocessing
data("AdultUCI")
AdultUCI[1:2,]
AdultUCI[["fnlwgt"]] <- NULL
AdultUCI[["education-num"]] <- NULL
AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),
labels = c("Young", "Middle-aged", "Senior", "Old"))
AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]],
c(0,25,40,60,168)), labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],
c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capitalgain"]]>0]),Inf)),
labels = c("None", "Low", "High"))
AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],
c(-Inf,0, median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capitalloss"]]>0]),Inf)),
labels = c("none", "low", "high"))ในการสร้างกฎโดยใช้อัลกอริทึม apriori เราจำเป็นต้องสร้างเมทริกซ์ธุรกรรม รหัสต่อไปนี้แสดงวิธีการทำใน R
# Convert the data into a transactions format
Adult <- as(AdultUCI, "transactions")
Adult
# transactions in sparse format with
# 48842 transactions (rows) and
# 115 items (columns)
summary(Adult)
# Plot frequent item-sets
itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)
# generate rules
min_support = 0.01
confidence = 0.6
rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))
rules
inspect(rules[100:110, ])
# lhs rhs support confidence lift
# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486
# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456
# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474
= United-States}แผนผังการตัดสินใจคืออัลกอริทึมที่ใช้สำหรับปัญหาการเรียนรู้ที่มีการดูแลเช่นการจำแนกประเภทหรือการถดถอย แผนผังการตัดสินใจหรือแผนผังการจำแนกคือต้นไม้ที่แต่ละโหนดภายใน (ที่ไม่ใช่ลีฟ) มีป้ายกำกับด้วยคุณลักษณะการป้อนข้อมูล ส่วนโค้งที่มาจากโหนดที่มีป้ายกำกับคุณลักษณะจะมีป้ายกำกับด้วยค่าที่เป็นไปได้แต่ละค่าของคุณลักษณะ แต่ละใบของต้นไม้มีป้ายกำกับชั้นเรียนหรือการแจกแจงความน่าจะเป็นเหนือชั้นเรียน
ต้นไม้สามารถ "เรียนรู้" ได้โดยการแยกชุดแหล่งที่มาออกเป็นส่วนย่อยตามการทดสอบค่าแอตทริบิวต์ กระบวนการนี้จะทำซ้ำในแต่ละส่วนย่อยที่ได้รับในลักษณะเรียกซ้ำที่เรียกว่าrecursive partitioning. การเรียกซ้ำจะเสร็จสมบูรณ์เมื่อเซ็ตย่อยที่โหนดมีค่าเดียวกันทั้งหมดของตัวแปรเป้าหมายหรือเมื่อการแยกจะไม่เพิ่มค่าให้กับการคาดคะเนอีกต่อไป กระบวนการเหนี่ยวนำจากบนลงล่างของทรีการตัดสินใจเป็นตัวอย่างของอัลกอริทึมโลภและเป็นกลยุทธ์ที่พบบ่อยที่สุดสำหรับการเรียนรู้ต้นไม้การตัดสินใจ
โครงสร้างการตัดสินใจที่ใช้ในการขุดข้อมูลมีสองประเภทหลัก -
Classification tree - เมื่อการตอบสนองเป็นตัวแปรเล็กน้อยเช่นอีเมลเป็นสแปมหรือไม่
Regression tree - เมื่อผลการทำนายถือได้ว่าเป็นจำนวนจริง (เช่นเงินเดือนของคนงาน)
ต้นไม้ตัดสินใจเป็นวิธีง่ายๆและด้วยเหตุนี้จึงมีปัญหา หนึ่งในประเด็นนี้คือความแปรปรวนที่สูงในแบบจำลองผลลัพธ์ที่ต้นไม้ตัดสินใจสร้างขึ้น เพื่อบรรเทาปัญหานี้ได้มีการพัฒนาวิธีการทั้งชุดของต้นไม้การตัดสินใจ ปัจจุบันมีวิธีการทั้งสองกลุ่มที่ใช้กันอย่างแพร่หลาย -
Bagging decision trees- ต้นไม้เหล่านี้ใช้เพื่อสร้างแผนผังการตัดสินใจหลาย ๆ ครั้งโดยการสุ่มตัวอย่างข้อมูลการฝึกอบรมซ้ำ ๆ พร้อมการแทนที่และการลงคะแนนต้นไม้เพื่อการทำนายที่เป็นเอกฉันท์ อัลกอริทึมนี้ถูกเรียกว่าฟอเรสต์แบบสุ่ม
Boosting decision trees- การส่งเสริมการไล่ระดับสีรวมผู้เรียนที่อ่อนแอ ในกรณีนี้ต้นไม้ตัดสินใจเป็นผู้เรียนที่เข้มแข็งเพียงคนเดียวในรูปแบบซ้ำ ๆ มันเหมาะกับต้นไม้ที่อ่อนแอต่อข้อมูลและคอยปรับผู้เรียนที่อ่อนแอซ้ำ ๆ เพื่อแก้ไขข้อผิดพลาดของโมเดลก่อนหน้านี้
# Install the party package
# install.packages('party')
library(party)
library(ggplot2)
head(diamonds)
# We will predict the cut of diamonds using the features available in the
diamonds dataset.
ct = ctree(cut ~ ., data = diamonds)
# plot(ct, main="Conditional Inference Tree")
# Example output
# Response: cut
# Inputs: carat, color, clarity, depth, table, price, x, y, z
# Number of observations: 53940
#
# 1) table <= 57; criterion = 1, statistic = 10131.878
# 2) depth <= 63; criterion = 1, statistic = 8377.279
# 3) table <= 56.4; criterion = 1, statistic = 226.423
# 4) z <= 2.64; criterion = 1, statistic = 70.393
# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48
# 6) color <= E; criterion = 0.997, statistic = 12.829
# 7)* weights = 82
# 6) color > E
#Table of prediction errors
table(predict(ct), diamonds$cut)
# Fair Good Very Good Premium Ideal
# Fair 1388 171 17 0 14
# Good 102 2912 499 26 27
# Very Good 54 998 3334 249 355
# Premium 44 711 5054 11915 1167
# Ideal 22 114 3178 1601 19988
# Estimated class probabilities
probs = predict(ct, newdata = diamonds, type = "prob")
probs = do.call(rbind, probs)
head(probs)การถดถอยโลจิสติกเป็นรูปแบบการจำแนกประเภทที่ตัวแปรตอบสนองเป็นหมวดหมู่ เป็นอัลกอริทึมที่มาจากสถิติและใช้สำหรับปัญหาการจำแนกประเภทภายใต้การดูแล ในการถดถอยโลจิสติกส์เราพยายามหาเวกเตอร์βของพารามิเตอร์ในสมการต่อไปนี้ที่ลดฟังก์ชันต้นทุนให้น้อยที่สุด
$$logit(p_i) = ln \left ( \frac{p_i}{1 - p_i} \right ) = \beta_0 + \beta_1x_{1,i} + ... + \beta_kx_{k,i}$$
รหัสต่อไปนี้แสดงให้เห็นถึงวิธีการปรับให้พอดีกับแบบจำลองการถดถอยโลจิสติกใน R เราจะใช้ที่นี่ชุดข้อมูลสแปมเพื่อแสดงการถดถอยโลจิสติกแบบเดียวกับที่ใช้สำหรับ Naive Bayes
จากผลการคาดการณ์ในแง่ของความแม่นยำเราพบว่าแบบจำลองการถดถอยมีความแม่นยำ 92.5% ในชุดทดสอบเทียบกับ 72% ที่ทำได้โดยตัวจำแนก Naive Bayes
library(ElemStatLearn)
head(spam)
# Split dataset in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.8))
train = spam[inx,]
test = spam[-inx,]
# Fit regression model
fit = glm(spam ~ ., data = train, family = binomial())
summary(fit)
# Call:
# glm(formula = spam ~ ., family = binomial(), data = train)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -4.5172 -0.2039 0.0000 0.1111 5.4944
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 ***
# A.1 -4.546e-01 2.560e-01 -1.776 0.075720 .
# A.2 -1.630e-01 7.731e-02 -2.108 0.035043 *
# A.3 1.487e-01 1.261e-01 1.179 0.238591
# A.4 2.055e+00 1.467e+00 1.401 0.161153
# A.5 6.165e-01 1.191e-01 5.177 2.25e-07 ***
# A.6 7.156e-01 2.768e-01 2.585 0.009747 **
# A.7 2.606e+00 3.917e-01 6.652 2.88e-11 ***
# A.8 6.750e-01 2.284e-01 2.955 0.003127 **
# A.9 1.197e+00 3.362e-01 3.559 0.000373 ***
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
### Make predictions
preds = predict(fit, test, type = ’response’)
preds = ifelse(preds > 0.5, 1, 0)
tbl = table(target = test$spam, preds)
tbl
# preds
# target 0 1
# email 535 23
# spam 46 316
sum(diag(tbl)) / sum(tbl)
# 0.925อนุกรมเวลาคือลำดับของการสังเกตตัวแปรเชิงหมวดหมู่หรือตัวเลขที่จัดทำดัชนีตามวันที่หรือการประทับเวลา ตัวอย่างที่ชัดเจนของข้อมูลอนุกรมเวลาคืออนุกรมเวลาของราคาหุ้น ในตารางต่อไปนี้เราจะเห็นโครงสร้างพื้นฐานของข้อมูลอนุกรมเวลา ในกรณีนี้การสังเกตจะถูกบันทึกทุกชั่วโมง
| การประทับเวลา | ราคาหุ้น |
|---|---|
| 2015-10-11 09:00:00 น | 100 |
| 2015-10-11 10:00:00 น | 110 |
| 2558-10-11 11:00:00 น | 105 |
| 2015-10-11 12:00:00 น | 90 |
| 2015-10-11 13:00:00 น | 120 |
โดยปกติขั้นตอนแรกในการวิเคราะห์อนุกรมเวลาคือการพล็อตอนุกรมซึ่งโดยปกติจะทำด้วยแผนภูมิเส้น
การประยุกต์ใช้การวิเคราะห์อนุกรมเวลาโดยทั่วไปคือการคาดการณ์มูลค่าในอนาคตของค่าตัวเลขโดยใช้โครงสร้างชั่วคราวของข้อมูล ซึ่งหมายความว่าการสังเกตที่มีอยู่จะใช้เพื่อทำนายค่าจากอนาคต
การจัดลำดับข้อมูลชั่วคราวหมายความว่าวิธีการถดถอยแบบดั้งเดิมไม่มีประโยชน์ ในการสร้างการคาดการณ์ที่มีประสิทธิภาพเราจำเป็นต้องมีโมเดลที่คำนึงถึงการจัดลำดับข้อมูลชั่วคราว
เรียกว่าโมเดลที่ใช้กันอย่างแพร่หลายสำหรับการวิเคราะห์อนุกรมเวลา Autoregressive Moving Average(ARMA) แบบจำลองประกอบด้วยสองส่วนคือautoregressive (AR) และก moving average(MA) ส่วน. จากนั้นโมเดลจะเรียกว่าโมเดลARMA (p, q)โดยที่pคือลำดับของส่วนที่ตอบสนองอัตโนมัติและqคือลำดับของส่วนค่าเฉลี่ยเคลื่อนที่
แบบจำลองอัตโนมัติ
AR (P)จะอ่านเป็นรูปแบบของการสั่งซื้ออัตพี ในทางคณิตศาสตร์เขียนว่า -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
โดยที่ {φ 1 , …, φ p } เป็นพารามิเตอร์ที่จะประมาณ c คือค่าคงที่และตัวแปรสุ่มε tแทนสัญญาณรบกวนสีขาว ข้อ จำกัด บางประการมีความจำเป็นต่อค่าของพารามิเตอร์เพื่อให้โมเดลอยู่นิ่ง
ค่าเฉลี่ยเคลื่อนที่
สัญกรณ์MA (q)หมายถึงโมเดลค่าเฉลี่ยเคลื่อนที่ของคำสั่งq -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
โดยที่θ 1 , ... , θ qเป็นพารามิเตอร์ของโมเดล, μคือความคาดหวังของ X tและε t , ε t - 1 , ... คือเงื่อนไขข้อผิดพลาดของสัญญาณรบกวนสีขาว
Autoregressive Moving Average
ARMA (P, Q)รุ่นรวม P ข้อกำหนดและเงื่อนไขอัต Q ย้ายค่าเฉลี่ย ในทางคณิตศาสตร์โมเดลจะแสดงด้วยสูตรต่อไปนี้ -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
เราจะเห็นได้ว่าARMA (P, Q)รูปแบบคือการรวมกันของAR (P)และซาชูเซตส์ (Q)รุ่น
เพื่อให้สัญชาตญาณของรูปแบบที่บางคนคิดว่าส่วน AR ของสมการพยายามที่จะประมาณค่าพารามิเตอร์สำหรับ X ที - ฉันสังเกตของเพื่อทำนายค่าของตัวแปรในเอ็กซ์ที ในที่สุดค่าเฉลี่ยถ่วงน้ำหนักของค่าในอดีต ส่วนซาชูเซตส์ใช้วิธีการเดียวกัน แต่มีข้อผิดพลาดของการสังเกตก่อนหน้านี้ε T - ฉัน ดังนั้นในท้ายที่สุดผลลัพธ์ของแบบจำลองคือค่าเฉลี่ยถ่วงน้ำหนัก
โค้ดต่อไปนี้แสดงให้เห็นถึงวิธีการที่จะดำเนินการARMA (P, Q) ในการวิจัย
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)การพล็อตข้อมูลเป็นขั้นตอนแรกเพื่อค้นหาว่ามีโครงสร้างชั่วคราวในข้อมูลหรือไม่ เราจะเห็นได้จากพล็อตว่ามีเดือยแหลมแรงในช่วงปลายปีของแต่ละปี
รหัสต่อไปนี้เหมาะกับโมเดล ARMA กับข้อมูล มันเรียกใช้โมเดลหลายชุดและเลือกรุ่นที่มีข้อผิดพลาดน้อยกว่า
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172ในบทนี้เราจะใช้ข้อมูลที่คัดลอกมาในส่วนที่ 1 ของหนังสือ ข้อมูลมีข้อความที่อธิบายโปรไฟล์ของฟรีแลนซ์และอัตรารายชั่วโมงที่พวกเขาเรียกเก็บเป็น USD แนวคิดของส่วนต่อไปนี้คือเพื่อให้เหมาะกับรูปแบบที่กำหนดทักษะของนักแปลอิสระเราสามารถคาดเดาเงินเดือนรายชั่วโมงได้
รหัสต่อไปนี้แสดงวิธีการแปลงข้อความดิบที่ในกรณีนี้มีทักษะของผู้ใช้ในเมทริกซ์ถุงคำ สำหรับสิ่งนี้เราใช้ห้องสมุด R ชื่อ tm ซึ่งหมายความว่าสำหรับแต่ละคำในคลังข้อมูลเราสร้างตัวแปรด้วยจำนวนครั้งที่เกิดขึ้นของแต่ละตัวแปร
library(tm)
library(data.table)
source('text_analytics/text_analytics_functions.R')
data = fread('text_analytics/data/profiles.txt')
rate = as.numeric(data$rate)
keep = !is.na(rate)
rate = rate[keep]
### Make bag of words of title and body
X_all = bag_words(data$user_skills[keep])
X_all = removeSparseTerms(X_all, 0.999)
X_all
# <<DocumentTermMatrix (documents: 389, terms: 1422)>>
# Non-/sparse entries: 4057/549101
# Sparsity : 99%
# Maximal term length: 80
# Weighting : term frequency - inverse document frequency (normalized) (tf-idf)
### Make a sparse matrix with all the data
X_all <- as_sparseMatrix(X_all)ตอนนี้เรามีข้อความที่แสดงเป็นเมทริกซ์แบบกระจัดกระจายแล้วเราสามารถใส่แบบจำลองที่จะให้คำตอบแบบเบาบางได้ ทางเลือกที่ดีสำหรับกรณีนี้คือการใช้ LASSO (ตัวดำเนินการเลือกและการหดตัวที่แน่นอนน้อยที่สุด) นี่คือแบบจำลองการถดถอยที่สามารถเลือกคุณลักษณะที่เกี่ยวข้องมากที่สุดเพื่อทำนายเป้าหมาย
train_inx = 1:200
X_train = X_all[train_inx, ]
y_train = rate[train_inx]
X_test = X_all[-train_inx, ]
y_test = rate[-train_inx]
# Train a regression model
library(glmnet)
fit <- cv.glmnet(x = X_train, y = y_train,
family = 'gaussian', alpha = 1,
nfolds = 3, type.measure = 'mae')
plot(fit)
# Make predictions
predictions = predict(fit, newx = X_test)
predictions = as.vector(predictions[,1])
head(predictions)
# 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367
# We can compute the mean absolute error for the test data
mean(abs(y_test - predictions))
# 15.02175ตอนนี้เรามีแบบจำลองที่กำหนดทักษะที่สามารถทำนายเงินเดือนรายชั่วโมงของฟรีแลนซ์ได้ หากมีการรวบรวมข้อมูลมากขึ้นประสิทธิภาพของโมเดลจะดีขึ้น แต่โค้ดสำหรับใช้ไปป์ไลน์นี้จะเหมือนกัน
การเรียนรู้ออนไลน์เป็นฟิลด์ย่อยของการเรียนรู้ของเครื่องที่ช่วยให้สามารถปรับขนาดโมเดลการเรียนรู้ภายใต้การดูแลเป็นชุดข้อมูลขนาดใหญ่ แนวคิดพื้นฐานคือเราไม่จำเป็นต้องอ่านข้อมูลทั้งหมดในหน่วยความจำเพื่อให้พอดีกับโมเดลเราจำเป็นต้องอ่านทีละอินสแตนซ์เท่านั้น
ในกรณีนี้เราจะแสดงวิธีใช้อัลกอริทึมการเรียนรู้ออนไลน์โดยใช้การถดถอยโลจิสติกส์ เช่นเดียวกับในอัลกอริทึมการเรียนรู้ภายใต้การดูแลส่วนใหญ่จะมีฟังก์ชันต้นทุนที่ลดลง ในการถดถอยโลจิสติกฟังก์ชันต้นทุนถูกกำหนดเป็น -
$$ J (\ theta) \: = \: \ frac {-1} {m} \ left [\ sum_ {i = 1} ^ {m} y ^ {(i)} บันทึก (h _ {\ theta} ( x ^ {(i)})) + (1 - y ^ {(i)}) บันทึก (1 - h _ {\ theta} (x ^ {(i)})) \ right] $$
โดยที่J (θ)แทนฟังก์ชันต้นทุนและh θ (x)แสดงถึงสมมติฐาน ในกรณีของการถดถอยโลจิสติกจะกำหนดด้วยสูตรต่อไปนี้ -
$$ h_ \ theta (x) = \ frac {1} {1 + e ^ {\ theta ^ T x}} $$
ตอนนี้เราได้กำหนดฟังก์ชันต้นทุนแล้วเราต้องหาอัลกอริทึมเพื่อย่อขนาด อัลกอริทึมที่ง่ายที่สุดในการบรรลุสิ่งนี้เรียกว่าการไล่ระดับสีแบบสุ่ม กฎการอัพเดตของอัลกอริทึมสำหรับน้ำหนักของแบบจำลองการถดถอยโลจิสติกถูกกำหนดเป็น -
$$ \ theta_j: = \ theta_j - \ alpha (h_ \ theta (x) - y) x $$
มีการใช้อัลกอริทึมต่อไปนี้หลายอย่าง แต่วิธีที่ใช้ในไลบรารีvowpal wabbitนั้นเป็นวิธีที่ได้รับการพัฒนามากที่สุด ไลบรารีอนุญาตให้ฝึกโมเดลการถดถอยขนาดใหญ่และใช้ RAM จำนวนน้อย ในคำพูดของผู้สร้างมีคำอธิบายว่า: "โครงการ Vowpal Wabbit (VW) เป็นระบบการเรียนรู้นอกระบบที่รวดเร็วซึ่งสนับสนุนโดย Microsoft Research และ (ก่อนหน้านี้) Yahoo! Research"
เราจะทำงานกับชุดข้อมูลไททานิกจาก a kaggleการแข่งขัน. ข้อมูลต้นฉบับสามารถพบได้ในไฟล์bda/part3/vwโฟลเดอร์ ที่นี่เรามีสองไฟล์ -
- เรามีข้อมูลการฝึกอบรม (train_titanic.csv) และ
- ข้อมูลที่ไม่มีป้ายกำกับเพื่อทำการคาดการณ์ใหม่ (test_titanic.csv)
ในการแปลงรูปแบบ csv เป็นไฟล์ vowpal wabbit รูปแบบการป้อนข้อมูลใช้ไฟล์ csv_to_vowpal_wabbit.pyสคริปต์ python คุณจะต้องติดตั้ง python สำหรับสิ่งนี้อย่างชัดเจน ไปที่ไฟล์bda/part3/vw เปิดเทอร์มินัลและดำเนินการคำสั่งต่อไปนี้ -
python csv_to_vowpal_wabbit.pyโปรดทราบว่าสำหรับส่วนนี้หากคุณใช้ windows คุณจะต้องติดตั้งบรรทัดคำสั่ง Unix ให้เข้าสู่เว็บไซต์cygwinสำหรับสิ่งนั้น
เปิดเทอร์มินัลและในโฟลเดอร์ bda/part3/vw และดำเนินการคำสั่งต่อไปนี้ -
vw train_titanic.vw -f model.vw --binary --passes 20 -c -q ff --sgd --l1
0.00000001 --l2 0.0000001 --learning_rate 0.5 --loss_function logisticให้เราแยกย่อยสิ่งที่โต้แย้งของ vw call หมายถึง.
-f model.vw - หมายความว่าเรากำลังบันทึกโมเดลในไฟล์ model.vw เพื่อทำการคาดการณ์ในภายหลัง
--binary - รายงานการสูญเสียเป็นการจำแนกไบนารีโดยมีป้ายกำกับ -1,1
--passes 20 - ข้อมูลถูกใช้ 20 ครั้งเพื่อเรียนรู้น้ำหนัก
-c - สร้างไฟล์แคช
-q ff - ใช้คุณสมบัติกำลังสองในเนมสเปซ f
--sgd - ใช้การอัปเดตการสืบเชื้อสายไล่ระดับสีสุ่มแบบสุ่ม / คลาสสิก / ธรรมดาเช่นไม่ปรับเปลี่ยนไม่เป็นมาตรฐานและไม่แปรผัน
--l1 --l2 - การทำให้เป็นมาตรฐานของ L1 และ L2
--learning_rate 0.5 - อัตราการเรียนรู้αasกำหนดไว้ในสูตรกฎการอัพเดต
โค้ดต่อไปนี้แสดงผลลัพธ์ของการรันโมเดลการถดถอยในบรรทัดคำสั่ง ในผลลัพธ์เราได้รับการสูญเสียบันทึกโดยเฉลี่ยและรายงานเล็กน้อยเกี่ยวกับประสิทธิภาพของอัลกอริทึม
-loss_function logistic
creating quadratic features for pairs: ff
using l1 regularization = 1e-08
using l2 regularization = 1e-07
final_regressor = model.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 1
power_t = 0.5
decay_learning_rate = 1
using cache_file = train_titanic.vw.cache
ignoring text input in favor of cache input
num sources = 1
average since example example current current current
loss last counter weight label predict features
0.000000 0.000000 1 1.0 -1.0000 -1.0000 57
0.500000 1.000000 2 2.0 1.0000 -1.0000 57
0.250000 0.000000 4 4.0 1.0000 1.0000 57
0.375000 0.500000 8 8.0 -1.0000 -1.0000 73
0.625000 0.875000 16 16.0 -1.0000 1.0000 73
0.468750 0.312500 32 32.0 -1.0000 -1.0000 57
0.468750 0.468750 64 64.0 -1.0000 1.0000 43
0.375000 0.281250 128 128.0 1.0000 -1.0000 43
0.351562 0.328125 256 256.0 1.0000 -1.0000 43
0.359375 0.367188 512 512.0 -1.0000 1.0000 57
0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h
0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h
0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h
0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h
finished run
number of examples per pass = 802
passes used = 11
weighted example sum = 8822
weighted label sum = -2288
average loss = 0.179775 h
best constant = -0.530826
best constant’s loss = 0.659128
total feature number = 427878ตอนนี้เราสามารถใช้ไฟล์ model.vw เราได้รับการฝึกฝนเพื่อสร้างการคาดการณ์ด้วยข้อมูลใหม่
vw -d test_titanic.vw -t -i model.vw -p predictions.txtการคาดคะเนที่สร้างขึ้นในคำสั่งก่อนหน้านี้ไม่ได้ถูกทำให้เป็นมาตรฐานเพื่อให้พอดีระหว่างช่วง [0, 1] ในการทำสิ่งนี้เราใช้การแปลงซิกมอยด์
# Read the predictions
preds = fread('vw/predictions.txt')
# Define the sigmoid function
sigmoid = function(x) {
1 / (1 + exp(-x))
}
probs = sigmoid(preds[[1]])
# Generate class labels
preds = ifelse(probs > 0.5, 1, 0)
head(preds)
# [1] 0 1 0 0 1 0