การวิเคราะห์ข้อมูลขนาดใหญ่ - การวิเคราะห์อนุกรมเวลา
อนุกรมเวลาคือลำดับของการสังเกตตัวแปรเชิงหมวดหมู่หรือตัวเลขที่จัดทำดัชนีตามวันที่หรือการประทับเวลา ตัวอย่างที่ชัดเจนของข้อมูลอนุกรมเวลาคืออนุกรมเวลาของราคาหุ้น ในตารางต่อไปนี้เราจะเห็นโครงสร้างพื้นฐานของข้อมูลอนุกรมเวลา ในกรณีนี้การสังเกตจะถูกบันทึกทุกชั่วโมง
| การประทับเวลา | ราคาหุ้น |
|---|---|
| 2015-10-11 09:00:00 น | 100 |
| 2015-10-11 10:00:00 น | 110 |
| 2558-10-11 11:00:00 น | 105 |
| 2015-10-11 12:00:00 น | 90 |
| 2015-10-11 13:00:00 น | 120 |
โดยปกติขั้นตอนแรกในการวิเคราะห์อนุกรมเวลาคือการพล็อตอนุกรมซึ่งโดยปกติจะทำด้วยแผนภูมิเส้น
การประยุกต์ใช้การวิเคราะห์อนุกรมเวลาโดยทั่วไปคือการคาดการณ์มูลค่าในอนาคตของค่าตัวเลขโดยใช้โครงสร้างชั่วคราวของข้อมูล ซึ่งหมายความว่าการสังเกตที่มีอยู่จะใช้ในการทำนายค่าจากอนาคต
การจัดลำดับข้อมูลชั่วคราวหมายความว่าวิธีการถดถอยแบบดั้งเดิมไม่มีประโยชน์ ในการสร้างการคาดการณ์ที่มีประสิทธิภาพเราจำเป็นต้องมีแบบจำลองที่คำนึงถึงการจัดลำดับข้อมูลชั่วคราว
เรียกว่าโมเดลที่ใช้กันอย่างแพร่หลายสำหรับการวิเคราะห์อนุกรมเวลา Autoregressive Moving Average(ARMA) แบบจำลองประกอบด้วยสองส่วนคือautoregressive (AR) และก moving average(MA) ส่วน. จากนั้นโมเดลจะเรียกว่าโมเดลARMA (p, q)โดยที่pคือลำดับของส่วนที่ตอบสนองอัตโนมัติและqคือลำดับของส่วนค่าเฉลี่ยเคลื่อนที่
แบบจำลองอัตโนมัติ
AR (P)จะอ่านเป็นรูปแบบของการสั่งซื้ออัตพี ในทางคณิตศาสตร์เขียนว่า -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
โดยที่ {φ 1 , …, φ p } เป็นพารามิเตอร์ที่จะประมาณ c คือค่าคงที่และตัวแปรสุ่มε tแทนค่าสัญญาณรบกวน ข้อ จำกัด บางประการจำเป็นสำหรับค่าของพารามิเตอร์เพื่อให้โมเดลอยู่นิ่ง
ค่าเฉลี่ยเคลื่อนที่
สัญกรณ์MA (q)หมายถึงโมเดลค่าเฉลี่ยเคลื่อนที่ของคำสั่งq -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
โดยที่θ 1 , ... , θ qเป็นพารามิเตอร์ของแบบจำลอง, μคือความคาดหวังของ X tและε t , ε t - 1 , ... คือข้อผิดพลาดของสัญญาณรบกวนสีขาว
Autoregressive Moving Average
ARMA (P, Q)รุ่นรวม P ข้อกำหนดและเงื่อนไขอัต Q ย้ายค่าเฉลี่ย ในทางคณิตศาสตร์โมเดลจะแสดงด้วยสูตรต่อไปนี้ -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
เราจะเห็นได้ว่าARMA (P, Q)รูปแบบคือการรวมกันของAR (P)และซาชูเซตส์ (Q)รุ่น
เพื่อให้สัญชาตญาณของรูปแบบที่บางคนคิดว่าส่วน AR ของสมการพยายามที่จะประมาณค่าพารามิเตอร์สำหรับ X ที - ฉันสังเกตของเพื่อทำนายค่าของตัวแปรในเอ็กซ์ที ในที่สุดค่าเฉลี่ยถ่วงน้ำหนักของค่าในอดีต ส่วนซาชูเซตส์ใช้วิธีการเดียวกัน แต่มีข้อผิดพลาดของการสังเกตก่อนหน้านี้ε T - ฉัน ดังนั้นในท้ายที่สุดผลลัพธ์ของแบบจำลองคือค่าเฉลี่ยถ่วงน้ำหนัก
โค้ดต่อไปนี้แสดงให้เห็นถึงวิธีการที่จะดำเนินการARMA (P, Q) ในการวิจัย
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)โดยปกติการพล็อตข้อมูลเป็นขั้นตอนแรกเพื่อค้นหาว่ามีโครงสร้างชั่วคราวในข้อมูลหรือไม่ เราจะเห็นได้จากพล็อตว่ามีเดือยแหลมแรงในช่วงปลายปีของแต่ละปี
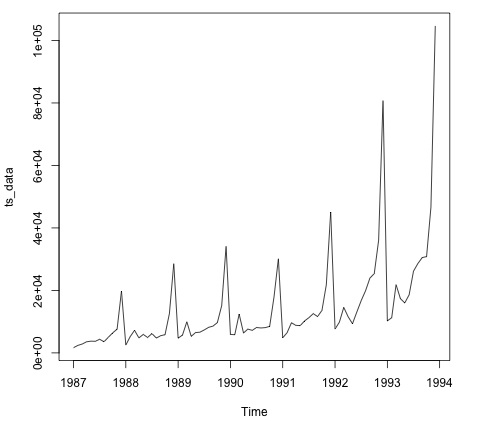
รหัสต่อไปนี้เหมาะกับโมเดล ARMA กับข้อมูล มันเรียกใช้โมเดลหลายชุดและเลือกรุ่นที่มีข้อผิดพลาดน้อยกว่า
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172