การวิเคราะห์ข้อมูลขนาดใหญ่ - แผนภูมิและกราฟ
แนวทางแรกในการวิเคราะห์ข้อมูลคือการวิเคราะห์ด้วยสายตา โดยปกติวัตถุประสงค์ในการทำเช่นนี้คือการหาความสัมพันธ์ระหว่างตัวแปรและคำอธิบายที่ไม่แปรผันของตัวแปร เราสามารถแบ่งกลยุทธ์เหล่านี้เป็น -
- การวิเคราะห์แบบ Univariate
- การวิเคราะห์หลายตัวแปร
วิธีการแบบกราฟิกที่แตกต่างกัน
Univariateเป็นคำศัพท์ทางสถิติ ในทางปฏิบัติหมายความว่าเราต้องการวิเคราะห์ตัวแปรโดยเป็นอิสระจากข้อมูลที่เหลือ แผนการที่อนุญาตให้ทำได้อย่างมีประสิทธิภาพ ได้แก่ -
กล่องพล็อต
โดยปกติ Box-Plots จะใช้เพื่อเปรียบเทียบการแจกแจง เป็นวิธีที่ดีในการตรวจสอบด้วยสายตาว่ามีความแตกต่างระหว่างการแจกแจงหรือไม่ เราสามารถดูได้ว่าราคาเพชรสำหรับการเจียระไนแบบต่างๆมีความแตกต่างกันหรือไม่
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)เราจะเห็นว่าในพล็อตมีความแตกต่างในการกระจายราคาเพชรในการเจียระไนประเภทต่างๆ

ฮิสโตแกรม
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()ผลลัพธ์ของโค้ดด้านบนจะเป็นดังนี้ -
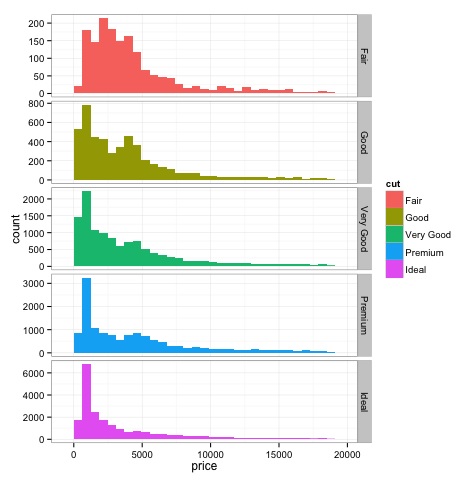
วิธีการแบบกราฟิกหลายตัวแปร
วิธีการแบบกราฟิกหลายตัวแปรในการวิเคราะห์ข้อมูลเชิงสำรวจมีวัตถุประสงค์ในการค้นหาความสัมพันธ์ระหว่างตัวแปรต่างๆ มีสองวิธีในการทำสิ่งนี้ให้สำเร็จซึ่งมักใช้: การพล็อตเมทริกซ์สหสัมพันธ์ของตัวแปรตัวเลขหรือเพียงแค่พล็อตข้อมูลดิบเป็นเมทริกซ์ของการกระจาย
เพื่อแสดงให้เห็นถึงสิ่งนี้เราจะใช้ชุดข้อมูลเพชร หากต้องการทำตามรหัสให้เปิดสคริปต์bda/part2/charts/03_multivariate_analysis.R.
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)รหัสจะสร้างผลลัพธ์ต่อไปนี้ -

นี่คือบทสรุปมันบอกเราว่ามีความสัมพันธ์ที่แข็งแกร่งระหว่างราคาและคาเร็ตและตัวแปรอื่น ๆ ไม่มากนัก
เมทริกซ์สหสัมพันธ์จะมีประโยชน์เมื่อเรามีตัวแปรจำนวนมากซึ่งในกรณีนี้การพล็อตข้อมูลดิบจะไม่สามารถใช้งานได้จริง ดังที่ได้กล่าวไว้สามารถแสดงข้อมูลดิบได้เช่นกัน -
library(GGally)
ggpairs(df)เราสามารถเห็นในพล็อตว่าผลลัพธ์ที่แสดงในแผนที่ความร้อนได้รับการยืนยันแล้วมีความสัมพันธ์ 0.922 ระหว่างตัวแปรราคาและกะรัต
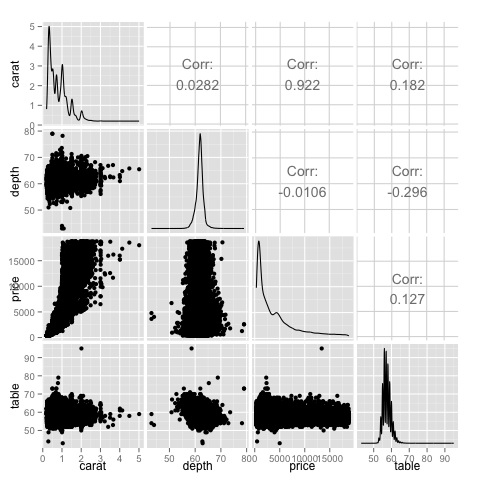
เป็นไปได้ที่จะเห็นภาพความสัมพันธ์นี้ในแผนภาพราคากะรัตที่อยู่ในดัชนี (3, 1) ของเมทริกซ์ scatterplot