กรมทรัพย์สินทางปัญญา - คู่มือฉบับย่อ
บทนำ
การประมวลผลสัญญาณเป็นระเบียบวินัยในวิศวกรรมไฟฟ้าและในคณิตศาสตร์ที่เกี่ยวข้องกับการวิเคราะห์และการประมวลผลสัญญาณแอนะล็อกและดิจิทัลและเกี่ยวข้องกับการจัดเก็บการกรองและการดำเนินการอื่น ๆ เกี่ยวกับสัญญาณ สัญญาณเหล่านี้รวมถึงสัญญาณส่งสัญญาณเสียงหรือเสียงสัญญาณภาพและสัญญาณอื่น ๆ เป็นต้น
จากสัญญาณเหล่านี้ทั้งหมดฟิลด์ที่เกี่ยวข้องกับประเภทของสัญญาณที่อินพุตเป็นรูปภาพและเอาต์พุตยังเป็นรูปภาพในการประมวลผลภาพ ตามชื่อมันเกี่ยวข้องกับการประมวลผลภาพ
สามารถแบ่งออกได้อีกเป็นการประมวลผลภาพอนาล็อกและการประมวลผลภาพดิจิทัล
การประมวลผลภาพอนาล็อก
การประมวลผลภาพแบบอะนาล็อกทำบนสัญญาณอนาล็อก รวมถึงการประมวลผลสัญญาณอนาล็อกสองมิติ ในการประมวลผลประเภทนี้ภาพจะถูกจัดการด้วยวิธีการทางไฟฟ้าโดยเปลี่ยนสัญญาณไฟฟ้า ตัวอย่างทั่วไป ได้แก่ ภาพโทรทัศน์
การประมวลผลภาพดิจิทัลมีผลเหนือกว่าการประมวลผลภาพแบบอะนาล็อกเมื่อเวลาผ่านไปเนื่องจากมีการใช้งานที่หลากหลาย
การประมวลผลภาพดิจิตอล
การประมวลผลภาพดิจิทัลเกี่ยวข้องกับการพัฒนาระบบดิจิทัลที่ดำเนินการกับภาพดิจิทัล
รูปภาพคืออะไร
ภาพไม่ได้เป็นเพียงสัญญาณสองมิติ มันถูกกำหนดโดยฟังก์ชันทางคณิตศาสตร์ f (x, y) โดยที่ x และ y เป็นสองพิกัดในแนวนอนและแนวตั้ง
ค่า f (x, y) ที่จุดใด ๆ จะให้ค่าพิกเซลที่จุดนั้นของภาพ

รูปด้านบนเป็นตัวอย่างของภาพดิจิทัลที่คุณกำลังดูอยู่บนหน้าจอคอมพิวเตอร์ของคุณ แต่จริงๆแล้วภาพนี้ไม่ใช่อะไรเลยนอกจากอาร์เรย์สองมิติของตัวเลขที่อยู่ระหว่าง 0 ถึง 255
| 128 | 30 | 123 |
| 232 | 123 | 321 |
| 123 | 77 | 89 |
| 80 | 255 | 255 |
ตัวเลขแต่ละตัวแทนค่าของฟังก์ชัน f (x, y) ณ จุดใดก็ได้ ในกรณีนี้ค่า 128, 230, 123 แต่ละค่าแทนค่าพิกเซลแต่ละรายการ ขนาดของรูปภาพเป็นขนาดของอาร์เรย์สองมิตินี้
ความสัมพันธ์ระหว่างภาพดิจิทัลและสัญญาณ
ถ้าภาพเป็นอาร์เรย์สองมิติแล้วสัญญาณจะทำอย่างไร? เพื่อที่จะเข้าใจว่าเราต้องเข้าใจก่อนว่าสัญญาณคืออะไร?
สัญญาณ
ในโลกทางกายภาพปริมาณใด ๆ ที่วัดได้ในช่วงเวลาเหนืออวกาศหรือมิติที่สูงกว่านั้นสามารถใช้เป็นสัญญาณได้ สัญญาณเป็นฟังก์ชันทางคณิตศาสตร์และสื่อถึงข้อมูลบางอย่าง สัญญาณอาจเป็นสัญญาณมิติเดียวหรือสองมิติหรือสูงกว่า สัญญาณมิติเดียวคือสัญญาณที่วัดตามช่วงเวลา ตัวอย่างทั่วไปคือสัญญาณเสียง สัญญาณสองมิติคือสัญญาณที่วัดได้จากปริมาณทางกายภาพอื่น ๆ ตัวอย่างของสัญญาณสองมิติคือภาพดิจิทัล เราจะดูรายละเอียดเพิ่มเติมในบทช่วยสอนถัดไปเกี่ยวกับวิธีการสร้างและตีความสัญญาณมิติเดียวหรือสองมิติและสัญญาณที่สูงกว่า
ความสัมพันธ์
เนื่องจากสิ่งใดก็ตามที่ถ่ายทอดข้อมูลหรือถ่ายทอดข้อความในโลกทางกายภาพระหว่างผู้สังเกตการณ์สองคนเป็นสัญญาณ ซึ่งรวมถึงเสียงพูดหรือ (เสียงของมนุษย์) หรือภาพเป็นสัญญาณ ตั้งแต่เมื่อเราพูดเสียงของเราจะถูกแปลงเป็นคลื่นเสียง / สัญญาณและเปลี่ยนไปตามเวลาที่เราพูดด้วย ไม่เพียงแค่นี้ แต่วิธีการทำงานของกล้องดิจิทัลด้วยในขณะที่การรับภาพจากกล้องดิจิทัลเกี่ยวข้องกับการถ่ายโอนสัญญาณจากส่วนหนึ่งของระบบไปยังอีกส่วนหนึ่ง
ภาพดิจิทัลเกิดขึ้นได้อย่างไร
เนื่องจากการจับภาพจากกล้องเป็นกระบวนการทางกายภาพ แสงแดดถูกใช้เป็นแหล่งพลังงาน อาร์เรย์เซ็นเซอร์ใช้สำหรับการได้มาของภาพ ดังนั้นเมื่อแสงแดดตกกระทบวัตถุปริมาณแสงที่สะท้อนจากวัตถุนั้นจะถูกตรวจจับโดยเซ็นเซอร์และสัญญาณแรงดันไฟฟ้าต่อเนื่องจะถูกสร้างขึ้นโดยปริมาณข้อมูลที่ตรวจจับได้ ในการสร้างภาพดิจิทัลเราจำเป็นต้องแปลงข้อมูลนี้ให้อยู่ในรูปแบบดิจิทัล สิ่งนี้เกี่ยวข้องกับการสุ่มตัวอย่างและการหาปริมาณ (จะกล่าวถึงในภายหลัง) ผลลัพธ์ของการสุ่มตัวอย่างและการหาปริมาณทำให้เกิดอาร์เรย์สองมิติหรือเมทริกซ์ของตัวเลขซึ่งไม่มีอะไรเลยนอกจากภาพดิจิทัล
เขตข้อมูลที่ทับซ้อนกัน
วิสัยทัศน์ของเครื่องจักร / คอมพิวเตอร์
วิชันซิสเต็มหรือการมองเห็นด้วยคอมพิวเตอร์เกี่ยวข้องกับการพัฒนาระบบที่อินพุตเป็นรูปภาพและเอาต์พุตเป็นข้อมูลบางส่วน ตัวอย่างเช่น: การพัฒนาระบบที่สแกนใบหน้ามนุษย์และเปิดล็อคทุกประเภท ระบบนี้จะเป็นแบบนี้

คอมพิวเตอร์กราฟิก
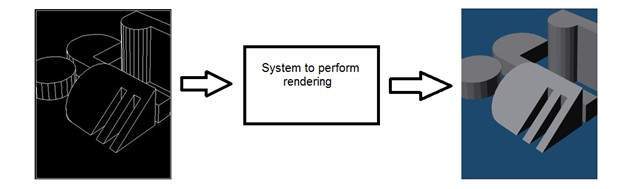
คอมพิวเตอร์กราฟิกเกี่ยวข้องกับการก่อตัวของภาพจากแบบจำลองวัตถุจากนั้นอุปกรณ์บางชนิดจะจับภาพ ตัวอย่างเช่น: การแสดงผลวัตถุ การสร้างภาพจากโมเดลวัตถุ ระบบดังกล่าวจะมีลักษณะเช่นนี้
ปัญญาประดิษฐ์
ปัญญาประดิษฐ์เป็นการศึกษาเกี่ยวกับการนำปัญญาของมนุษย์มาเป็นเครื่องจักรไม่มากก็น้อย ปัญญาประดิษฐ์มีแอพพลิเคชั่นมากมายในการประมวลผลภาพ ตัวอย่างเช่นการพัฒนาระบบคอมพิวเตอร์ช่วยในการวินิจฉัยที่ช่วยแพทย์ในการตีความภาพของ X-ray, MRI และอื่น ๆ จากนั้นจึงเน้นส่วนที่เด่นชัดเพื่อให้แพทย์ตรวจ
การประมวลผลสัญญาณ
การประมวลผลสัญญาณเป็นร่มและการประมวลผลภาพอยู่ข้างใต้ ปริมาณแสงที่สะท้อนจากวัตถุในโลกทางกายภาพ (โลก 3 มิติ) จะผ่านเลนส์ของกล้องและกลายเป็นสัญญาณ 2 มิติและส่งผลให้เกิดการสร้างภาพ จากนั้นภาพนี้จะถูกแปลงเป็นดิจิทัลโดยใช้วิธีการประมวลผลสัญญาณจากนั้นภาพดิจิทัลนี้จะถูกจัดการในการประมวลผลภาพดิจิทัล
บทช่วยสอนนี้ครอบคลุมพื้นฐานของสัญญาณและระบบที่จำเป็นสำหรับการทำความเข้าใจแนวคิดของการประมวลผลภาพดิจิทัล ก่อนที่จะเข้าสู่แนวคิดรายละเอียดก่อนอื่นให้กำหนดคำศัพท์ง่ายๆ
สัญญาณ
ในวิศวกรรมไฟฟ้าปริมาณพื้นฐานของการแสดงข้อมูลบางอย่างเรียกว่าสัญญาณ ไม่สำคัญว่าข้อมูลนั้นคืออะไร: ข้อมูลอนาล็อกหรือดิจิทัล ในทางคณิตศาสตร์สัญญาณเป็นฟังก์ชันที่ถ่ายทอดข้อมูลบางอย่าง ในความเป็นจริงปริมาณใด ๆ ที่วัดได้ตลอดเวลาในอวกาศหรือมิติที่สูงกว่านั้นสามารถนำมาเป็นสัญญาณได้ สัญญาณอาจมีขนาดใดก็ได้และอาจอยู่ในรูปแบบใดก็ได้
สัญญาณอนาล็อก
สัญญาณอาจเป็นปริมาณอะนาล็อกซึ่งหมายความว่ามีการกำหนดตามเวลา มันเป็นสัญญาณต่อเนื่อง สัญญาณเหล่านี้กำหนดไว้เหนือตัวแปรอิสระต่อเนื่อง วิเคราะห์ได้ยากเนื่องจากมีค่าเป็นจำนวนมาก มีความแม่นยำมากเนื่องจากมีตัวอย่างค่าจำนวนมาก ในการจัดเก็บสัญญาณเหล่านี้คุณต้องใช้หน่วยความจำที่ไม่มีที่สิ้นสุดเนื่องจากสามารถบรรลุค่าที่ไม่มีที่สิ้นสุดบนเส้นจริง สัญญาณแอนะล็อกแสดงโดยคลื่นบาป
ตัวอย่างเช่น:
เสียงของมนุษย์
เสียงของมนุษย์เป็นตัวอย่างของสัญญาณอนาล็อก เมื่อคุณพูดเสียงที่เกิดขึ้นจะเดินทางผ่านอากาศในรูปของคลื่นความดันดังนั้นจึงเป็นของฟังก์ชันทางคณิตศาสตร์โดยมีตัวแปรอิสระของพื้นที่และเวลาและค่าที่สอดคล้องกับความกดอากาศ
อีกตัวอย่างหนึ่งคือคลื่นบาปซึ่งแสดงในรูปด้านล่าง
Y = sin (x) โดยที่ x เป็นค่าไม่ระบุ

สัญญาณดิจิตอล
เมื่อเปรียบเทียบกับสัญญาณแอนะล็อกสัญญาณดิจิทัลนั้นวิเคราะห์ได้ง่ายมาก เป็นสัญญาณที่ไม่ต่อเนื่อง พวกเขาคือการจัดสรรสัญญาณอนาล็อก
คำว่าดิจิทัลย่อมาจากค่าที่ไม่ต่อเนื่องและด้วยเหตุนี้จึงหมายความว่าพวกเขาใช้ค่าเฉพาะเพื่อแสดงข้อมูลใด ๆ ในสัญญาณดิจิทัลจะใช้เพียงสองค่าเพื่อแสดงบางสิ่งเช่น: 1 และ 0 (ค่าไบนารี) สัญญาณดิจิทัลมีความแม่นยำน้อยกว่าเมื่อเทียบกับสัญญาณอนาล็อกเนื่องจากเป็นตัวอย่างที่ไม่ต่อเนื่องของสัญญาณแอนะล็อกในช่วงเวลาหนึ่ง อย่างไรก็ตามสัญญาณดิจิตอลจะไม่มีสัญญาณรบกวน ดังนั้นจึงอยู่ได้นานและง่ายต่อการตีความ สัญญาณดิจิทัลแสดงด้วยคลื่นสี่เหลี่ยม
ตัวอย่างเช่น:
แป้นพิมพ์คอมพิวเตอร์
เมื่อใดก็ตามที่กดปุ่มจากแป้นพิมพ์สัญญาณไฟฟ้าที่เหมาะสมจะถูกส่งไปยังตัวควบคุมแป้นพิมพ์ที่มีค่า ASCII คีย์นั้น ๆ ตัวอย่างเช่นสัญญาณไฟฟ้าที่สร้างขึ้นเมื่อกดปุ่มแป้นพิมพ์ a จะมีข้อมูลของตัวเลข 97 ในรูปแบบ 0 และ 1 ซึ่งเป็นค่า ASCII ของอักขระ a
ความแตกต่างระหว่างสัญญาณอนาล็อกและดิจิตอล
| องค์ประกอบการเปรียบเทียบ | สัญญาณอนาล็อก | สัญญาณดิจิตอล |
|---|---|---|
| การวิเคราะห์ | ยาก | วิเคราะห์ได้ |
| การเป็นตัวแทน | ต่อเนื่อง | ไม่ต่อเนื่อง |
| ความถูกต้อง | แม่นยำมากขึ้น | แม่นยำน้อยกว่า |
| การจัดเก็บ | หน่วยความจำไม่มีที่สิ้นสุด | จัดเก็บได้อย่างง่ายดาย |
| ขึ้นอยู่กับเสียงรบกวน | ใช่ | ไม่ |
| เทคนิคการบันทึก | สัญญาณดั้งเดิมจะถูกรักษาไว้ | ตัวอย่างของสัญญาณจะถูกถ่ายและเก็บรักษาไว้ |
| ตัวอย่าง | เสียงของมนุษย์เทอร์โมมิเตอร์โทรศัพท์อนาล็อก ฯลฯ | คอมพิวเตอร์โทรศัพท์ดิจิทัลปากกาดิจิทัล ฯลฯ |
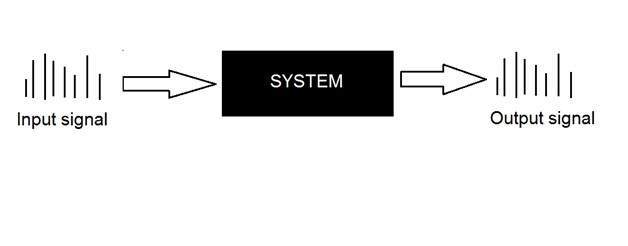
ระบบ
ระบบถูกกำหนดโดยประเภทของอินพุตและเอาต์พุตที่เกี่ยวข้อง เนื่องจากเรากำลังจัดการกับสัญญาณดังนั้นในกรณีของเราระบบของเราจะเป็นแบบจำลองทางคณิตศาสตร์ชิ้นส่วนของรหัส / ซอฟต์แวร์หรืออุปกรณ์ทางกายภาพหรือกล่องดำที่อินพุตเป็นสัญญาณและจะทำการประมวลผลบางอย่างกับสัญญาณนั้น และเอาต์พุตเป็นสัญญาณ อินพุตเรียกว่าการกระตุ้นและเอาต์พุตเรียกว่าการตอบสนอง

ในรูปด้านบนระบบได้แสดงให้เห็นว่าอินพุตและเอาต์พุตทั้งสองเป็นสัญญาณ แต่อินพุตเป็นสัญญาณอนาล็อก และเอาต์พุตเป็นสัญญาณดิจิตอล หมายความว่าระบบของเราเป็นระบบการแปลงที่แปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัล
มาดูด้านในของระบบกล่องดำนี้กัน
การแปลงสัญญาณอนาล็อกเป็นดิจิตอล
เนื่องจากมีแนวคิดมากมายที่เกี่ยวข้องกับการแปลงอนาล็อกเป็นดิจิทัลและในทางกลับกัน เราจะพูดถึงเฉพาะผู้ที่เกี่ยวข้องกับการประมวลผลภาพดิจิทัลเท่านั้น มีสองแนวคิดหลักที่เกี่ยวข้องกับการครอบคลุม
Sampling
Quantization
การสุ่มตัวอย่าง
การสุ่มตัวอย่างตามชื่อที่แนะนำสามารถกำหนดได้ว่าเป็นตัวอย่าง เก็บตัวอย่างสัญญาณดิจิทัลบนแกน x การสุ่มตัวอย่างทำได้บนตัวแปรอิสระ ในกรณีของสมการทางคณิตศาสตร์นี้:
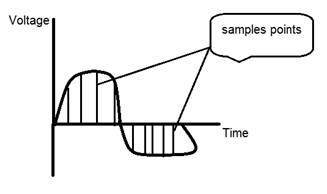
ทำการสุ่มตัวอย่างบนตัวแปร x นอกจากนี้เรายังสามารถกล่าวได้ว่าการแปลงแกน x (ค่าอนันต์) เป็นดิจิทัลทำได้ภายใต้การสุ่มตัวอย่าง
การสุ่มตัวอย่างแบ่งออกเป็นการสุ่มตัวอย่างขึ้นและการสุ่มตัวอย่างลง หากช่วงของค่าบนแกน x น้อยกว่าเราจะเพิ่มตัวอย่างของค่า สิ่งนี้เรียกว่าการสุ่มตัวอย่างขึ้นและในทางกลับกันเรียกว่าการสุ่มตัวอย่างลง
Quantization
Quantization ตามชื่อที่แนะนำสามารถกำหนดเป็นการแบ่งออกเป็น quanta (พาร์ติชัน) Quantization ทำโดยตัวแปรตาม มันตรงข้ามกับการสุ่มตัวอย่าง
ในกรณีของสมการทางคณิตศาสตร์นี้ y = sin (x)
Quantization ทำกับตัวแปร Y มันทำบนแกน y การแปลงค่าอนันต์แกน y เป็น 1, 0, -1 (หรือระดับอื่น ๆ ) เรียกว่า Quantization
ต่อไปนี้เป็นขั้นตอนพื้นฐานสองขั้นตอนที่เกี่ยวข้องในขณะที่แปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัล
การหาปริมาณของสัญญาณแสดงไว้ในรูปด้านล่าง
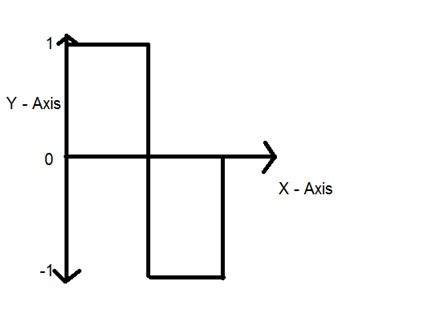
ทำไมเราต้องแปลงสัญญาณอนาล็อกเป็นสัญญาณดิจิตอล
เหตุผลแรกและชัดเจนคือการประมวลผลภาพดิจิทัลเกี่ยวข้องกับภาพดิจิทัลนั่นคือสัญญาณดิจิทัล ดังนั้นเมื่อจับภาพได้ทุกครั้งภาพจะถูกแปลงเป็นรูปแบบดิจิทัลจากนั้นจึงประมวลผล
เหตุผลประการที่สองและสำคัญคือในการดำเนินการกับสัญญาณแอนะล็อกกับคอมพิวเตอร์ดิจิทัลคุณต้องเก็บสัญญาณแอนะล็อกนั้นไว้ในคอมพิวเตอร์ และในการจัดเก็บสัญญาณอะนาล็อกจำเป็นต้องใช้หน่วยความจำที่ไม่มีที่สิ้นสุดในการจัดเก็บ และเนื่องจากเป็นไปไม่ได้ดังนั้นเราจึงแปลงสัญญาณนั้นเป็นรูปแบบดิจิทัลแล้วเก็บไว้ในคอมพิวเตอร์ดิจิทัลจากนั้นจึงดำเนินการกับสัญญาณนั้น
ระบบต่อเนื่องกับระบบไม่ต่อเนื่อง
ระบบต่อเนื่อง
ประเภทของระบบที่อินพุตและเอาต์พุตทั้งสองเป็นสัญญาณต่อเนื่องหรือสัญญาณอะนาล็อกเรียกว่าระบบต่อเนื่อง
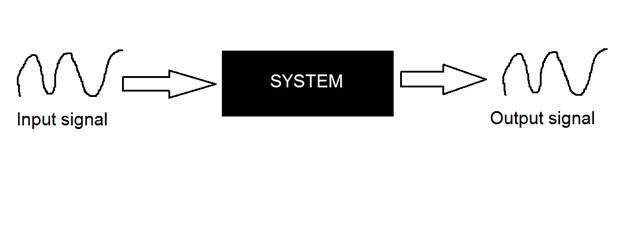
ระบบไม่ต่อเนื่อง
ประเภทของระบบที่อินพุตและเอาต์พุตทั้งสองเป็นสัญญาณไม่ต่อเนื่องหรือสัญญาณดิจิทัลเรียกว่าระบบดิจิทัล
ต้นกำเนิดของกล้องถ่ายรูป
ประวัติของกล้องและการถ่ายภาพไม่เหมือนกันอย่างแน่นอน แนวคิดของกล้องถูกนำมาใช้มากก่อนแนวคิดของการถ่ายภาพ
กล้อง Obscura
ประวัติของกล้องอยู่ในเอเชีย หลักการของกล้องถูกนำมาใช้ครั้งแรกโดยนักปรัชญาชาวจีน MOZI เป็นที่รู้จักกันในชื่อกล้องปิดบัง กล้องพัฒนามาจากหลักการนี้
คำว่า Camera Obscura พัฒนามาจากคำสองคำที่แตกต่างกัน กล้องและออบสคิวรา ความหมายของคำว่ากล้องคือห้องหรือห้องนิรภัยบางชนิดและ Obscura หมายถึงความมืด
แนวคิดที่ปราชญ์ชาวจีนนำมาใช้ประกอบด้วยอุปกรณ์ที่ฉายภาพโดยรอบบนผนัง อย่างไรก็ตามมันไม่ได้สร้างโดยชาวจีน
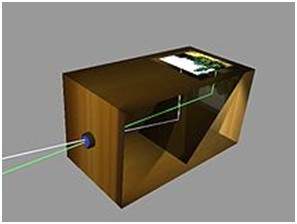
การสร้างกล้องปิดบัง
แนวคิดของภาษาจีนถูกนำมาสู่ความเป็นจริงโดยนักวิทยาศาสตร์มุสลิม Abu Ali Al-Hassan Ibn al-Haitham ที่รู้จักกันทั่วไปในชื่อ Ibn al-Haitham เขาสร้างกล้องถ่ายรูปตัวแรก กล้องของเขาเป็นไปตามหลักการของกล้องรูเข็ม เขาสร้างอุปกรณ์นี้ในที่ไหนสักแห่งประมาณ 1,000
กล้องพกพา
ในปี 1685 โยฮันน์ซาห์นสร้างกล้องแบบพกพาตัวแรก ก่อนการถือกำเนิดของอุปกรณ์นี้กล้องมีขนาดห้องและไม่สามารถพกพาได้ แม้ว่าอุปกรณ์จะถูกสร้างขึ้นโดยนักวิทยาศาสตร์ชาวไอริช Robert Boyle และ Robert Hooke ซึ่งเป็นกล้องที่สามารถพกพาได้ แต่อุปกรณ์นั้นก็ยังคงมีขนาดใหญ่มากในการพกพาจากที่หนึ่งไปอีกที่
ที่มาของการถ่ายภาพ
แม้ว่ากล้องปิดบังจะสร้างขึ้นในปี 1000 โดยนักวิทยาศาสตร์มุสลิม แต่การใช้งานจริงครั้งแรกถูกอธิบายไว้ในศตวรรษที่ 13 โดยโรเจอร์เบคอนนักปรัชญาชาวอังกฤษ โรเจอร์แนะนำให้ใช้กล้องในการสังเกตสุริยุปราคา
ดาวินชี
แม้ว่าจะมีการปรับปรุงอย่างมากก่อนศตวรรษที่ 15 แต่การปรับปรุงและการค้นพบของ Leonardo di ser Piero da Vinci นั้นน่าทึ่งมาก ดาวินชีเป็นศิลปินนักดนตรีนักกายวิภาคศาสตร์และนักสงครามที่ยิ่งใหญ่ เขาได้รับเครดิตสำหรับสิ่งประดิษฐ์มากมาย ภาพวาดที่มีชื่อเสียงที่สุดชิ้นหนึ่งของเขา ได้แก่ ภาพวาดโมนาลิซา

Da Vinci ไม่เพียง แต่สร้างกล้องปิดบังตามหลักการของกล้องรูเข็มเท่านั้น แต่ยังใช้เป็นอุปกรณ์ช่วยในการวาดภาพสำหรับงานศิลปะของเขาด้วย ในผลงานของเขาซึ่งอธิบายไว้ใน Codex Atlanticus มีการกำหนดหลักการของกล้องถ่ายรูปมากมาย
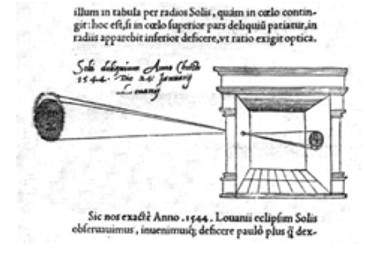
กล้องของเขาเป็นไปตามหลักการของกล้องรูเข็มซึ่งสามารถอธิบายได้ว่า
เมื่อภาพของวัตถุที่ส่องสว่างทะลุผ่านรูเล็ก ๆ เข้าไปในห้องที่มืดมากคุณจะเห็น [บนผนังด้านตรงข้าม] วัตถุเหล่านี้ในรูปแบบและสีที่เหมาะสมลดขนาดลงในตำแหน่งที่กลับด้านเนื่องจากการตัดกันของรังสี
ภาพแรก
ภาพแรกถ่ายเมื่อปี พ.ศ. 2357 โดยนักประดิษฐ์ชาวฝรั่งเศส Joseph Nicephore Niepce เขาถ่ายภาพแรกของมุมมองจากหน้าต่างที่ Le Gras โดยการเคลือบแผ่นพิวเตอร์ด้วยน้ำมันดินและหลังจากนั้นให้แผ่นนั้นสัมผัสกับแสง

ภาพถ่ายใต้น้ำครั้งแรก
ภาพถ่ายใต้น้ำภาพแรกถ่ายโดยวิลเลียมทอมสันนักคณิตศาสตร์ชาวอังกฤษโดยใช้กล่องกันน้ำ สิ่งนี้ทำในปีพ. ศ. 2399

ที่มาของภาพยนตร์
ต้นกำเนิดของภาพยนตร์ได้รับการแนะนำโดยนักประดิษฐ์ชาวอเมริกันและผู้ใจบุญที่รู้จักกันในชื่อ George Eastman ซึ่งถือได้ว่าเป็นผู้บุกเบิกการถ่ายภาพ
เขาก่อตั้ง บริษัท ชื่อ Eastman Kodak ซึ่งมีชื่อเสียงในด้านการพัฒนาภาพยนตร์ บริษัท เริ่มผลิตฟิล์มกระดาษในปี พ.ศ. 2428 เขาสร้างกล้อง Kodak ขึ้นมาเป็นครั้งแรกจากนั้นจึงทำบราวนี่ Brownie เป็นกล้องถ่ายรูปแบบกล่องและได้รับความนิยมเนื่องจากคุณสมบัติของ Snapshot

หลังจากการถือกำเนิดของภาพยนตร์เรื่องนี้อุตสาหกรรมกล้องถ่ายรูปก็เติบโตขึ้นอีกครั้งและสิ่งประดิษฐ์หนึ่งก็นำไปสู่อีกสิ่งหนึ่ง
Leica และ Argus
Leica และ argus เป็นกล้องอนาล็อกสองตัวที่พัฒนาในปี 2468 และปี 2482 ตามลำดับ กล้อง Leica สร้างขึ้นโดยใช้ฟิล์มขนาด 35 มม.

Argus เป็นกล้องอะนาล็อกอีกตัวหนึ่งที่ใช้รูปแบบ 35 มม. และมีราคาค่อนข้างถูกเมื่อเทียบกับ Leica และได้รับความนิยมอย่างมาก

กล้องวงจรปิดแบบอนาล็อก
ในปีพ. ศ. 2485 วิศวกรชาวเยอรมัน Walter Bruch ได้พัฒนาและติดตั้งระบบแรกของกล้องวงจรปิดแบบอนาล็อก เขายังได้รับเครดิตจากการประดิษฐ์โทรทัศน์สีในปี 1960
ภาพ Pac
กล้องถ่ายรูปแบบใช้แล้วทิ้งตัวแรกเปิดตัวในปีพ. ศ. 2492 โดย Photo Pac กล้องนี้เป็นกล้องที่ใช้งานได้เพียงครั้งเดียวโดยมีม้วนฟิล์มอยู่แล้ว Photo pac รุ่นต่อมาสามารถกันน้ำได้และยังมีแฟลชอีกด้วย

กล้องดิจิตอล
Mavica โดย Sony
Mavica (กล้องวิดีโอแม่เหล็ก) เปิดตัวโดย Sony ในปี 1981 เป็นตัวเปลี่ยนเกมตัวแรกในโลกกล้องดิจิทัล ภาพถูกบันทึกลงในฟล็อปปี้ดิสก์และสามารถดูภาพได้ในภายหลังบนหน้าจอมอนิเตอร์ใด ๆ
ไม่ใช่กล้องดิจิตอลล้วน แต่เป็นกล้องอนาล็อก แต่ได้รับความนิยมเนื่องจากมีความสามารถในการจัดเก็บภาพบนฟล็อปปี้ดิสก์ หมายความว่าตอนนี้คุณสามารถจัดเก็บภาพได้เป็นระยะเวลานานและคุณสามารถบันทึกภาพจำนวนมากบนฟลอปปีซึ่งจะถูกแทนที่ด้วยแผ่นดิสก์เปล่าแผ่นใหม่เมื่อเต็ม Mavica มีความจุในการจัดเก็บภาพ 25 ภาพในดิสก์
สิ่งที่สำคัญอีกอย่างหนึ่งที่ mavica แนะนำคือความจุ 0.3 เมกะพิกเซลในการถ่ายภาพ

กล้องดิจิตอล
Fuji DS-1P camera โดยฟิล์มฟูจิปี 1988 เป็นกล้องดิจิทัลตัวแรกที่แท้จริง
Nikon D1 เป็นกล้อง 2.74 ล้านพิกเซลและเป็นกล้องดิจิตอล SLR เชิงพาณิชย์ตัวแรกที่พัฒนาโดย Nikon และมีราคาไม่แพงมากสำหรับมืออาชีพ

ปัจจุบันกล้องดิจิตอลรวมอยู่ในโทรศัพท์มือถือที่มีความละเอียดและคุณภาพสูงมาก
เนื่องจากการประมวลผลภาพดิจิทัลมีแอพพลิเคชั่นที่กว้างมากและเกือบทุกสาขาทางเทคนิคได้รับผลกระทบจาก DIP เราจะพูดถึงแอพพลิเคชั่นหลัก ๆ ของ DIP
การประมวลผลภาพดิจิทัลไม่ได้ จำกัด เพียงแค่การปรับความละเอียดเชิงพื้นที่ของภาพในชีวิตประจำวันที่กล้องถ่าย ไม่ได้ จำกัด เพียงแค่การเพิ่มความสว่างของภาพถ่ายเท่านั้น แต่ยังมีมากกว่านั้นอีกด้วย
คลื่นแม่เหล็กไฟฟ้าสามารถคิดได้ว่าเป็นกระแสของอนุภาคที่อนุภาคแต่ละอนุภาคเคลื่อนที่ด้วยความเร็วแสง อนุภาคแต่ละตัวมีกลุ่มพลังงาน กลุ่มของพลังงานนี้เรียกว่าโฟตอน
สเปกตรัมแม่เหล็กไฟฟ้าตามพลังงานของโฟตอนแสดงไว้ด้านล่าง

ในสเปกตรัมแม่เหล็กไฟฟ้านี้เราสามารถมองเห็นได้เฉพาะสเปกตรัมที่มองเห็นได้ สเปกตรัมที่มองเห็นได้ส่วนใหญ่ประกอบด้วยสีที่แตกต่างกันเจ็ดสีซึ่งโดยทั่วไปเรียกว่า (VIBGOYR) VIBGOYR ย่อมาจากสีม่วงครามน้ำเงินเขียวส้มเหลืองและแดง
แต่นั่นไม่ได้ทำให้สิ่งอื่น ๆ ในสเปกตรัมเป็นโมฆะ ตามนุษย์ของเราสามารถมองเห็นได้เฉพาะส่วนที่มองเห็นได้ซึ่งเราเห็นวัตถุทั้งหมด แต่กล้องสามารถมองเห็นสิ่งอื่น ๆ ที่ตาเปล่าไม่สามารถมองเห็นได้ ตัวอย่างเช่นรังสีเอกซ์รังสีแกมมา ฯลฯ ดังนั้นการวิเคราะห์ทุกสิ่งนั้นก็ทำในการประมวลผลภาพดิจิทัลเช่นกัน
การสนทนานี้นำไปสู่คำถามอื่นซึ่งก็คือ
ทำไมเราต้องวิเคราะห์สิ่งอื่น ๆ ทั้งหมดในสเปกตรัม EM ด้วย?
คำตอบสำหรับคำถามนี้อยู่ในความจริงเนื่องจากสิ่งอื่น ๆ เช่น XRay ถูกนำมาใช้กันอย่างแพร่หลายในด้านการแพทย์ การวิเคราะห์รังสีแกมมามีความจำเป็นเนื่องจากมีการใช้กันอย่างแพร่หลายในเวชศาสตร์นิวเคลียร์และการสังเกตทางดาราศาสตร์ เช่นเดียวกันกับสิ่งที่เหลือในสเปกตรัม EM
การประยุกต์ใช้การประมวลผลภาพดิจิทัล
สาขาหลักบางสาขาที่ใช้กันอย่างแพร่หลายในการประมวลผลภาพดิจิทัลมีการกล่าวถึงด้านล่าง
การเพิ่มความคมชัดและการฟื้นฟูภาพ
ด้านการแพทย์
การสำรวจระยะไกล
การส่งและการเข้ารหัส
วิสัยทัศน์ของเครื่องจักร / หุ่นยนต์
การประมวลผลสี
การจดจำรูปแบบ
การประมวลผลวิดีโอ
การถ่ายภาพด้วยกล้องจุลทรรศน์
Others
การเพิ่มความคมชัดและการฟื้นฟูภาพ
การเพิ่มความคมชัดและการคืนค่าภาพหมายถึงการประมวลผลภาพที่ถ่ายจากกล้องสมัยใหม่เพื่อทำให้ได้ภาพที่ดีขึ้นหรือเพื่อปรับแต่งภาพเหล่านั้นเพื่อให้ได้ผลลัพธ์ที่ต้องการ หมายถึงการทำในสิ่งที่ Photoshop มักทำ
ซึ่งรวมถึงการซูมการเบลอการทำให้คมชัดระดับสีเทาเป็นการแปลงสีการตรวจจับขอบและในทางกลับกันการดึงภาพและการจดจำภาพ ตัวอย่างทั่วไป ได้แก่ :
ภาพต้นฉบับ

ภาพที่ซูม

ภาพเบลอ

ภาพคมชัด

ขอบ

ด้านการแพทย์
การใช้งานทั่วไปของ DIP ในด้านการแพทย์คือ
การถ่ายภาพรังสีแกมมา
สแกน PET
การถ่ายภาพเอ็กซ์เรย์
CT ทางการแพทย์
การถ่ายภาพ UV
การถ่ายภาพ UV
ในด้านการสำรวจระยะไกลพื้นที่ของโลกจะถูกสแกนโดยดาวเทียมหรือจากที่สูงมากจากนั้นจึงวิเคราะห์เพื่อให้ได้ข้อมูลเกี่ยวกับมัน การประยุกต์ใช้การประมวลผลภาพดิจิทัลโดยเฉพาะอย่างยิ่งในด้านการสำรวจระยะไกลคือการตรวจจับความเสียหายของโครงสร้างพื้นฐานที่เกิดจากแผ่นดินไหว
เนื่องจากต้องใช้เวลานานขึ้นในการทำความเข้าใจความเสียหายแม้ว่าจะเน้นที่ความเสียหายร้ายแรงก็ตาม เนื่องจากบางครั้งพื้นที่ที่ได้รับผลกระทบจากแผ่นดินไหวมีความกว้างมากจนไม่สามารถตรวจสอบด้วยตามนุษย์เพื่อประเมินความเสียหายได้ แม้ว่าจะเป็นอย่างนั้นก็เป็นขั้นตอนที่เร่งรีบและใช้เวลานานมาก ดังนั้นวิธีแก้ปัญหานี้จึงพบได้ในการประมวลผลภาพดิจิทัล ภาพของพื้นที่ที่ได้รับผลกระทบถูกจับจากพื้นดินด้านบนจากนั้นจึงวิเคราะห์เพื่อตรวจจับความเสียหายประเภทต่างๆที่เกิดจากแผ่นดินไหว
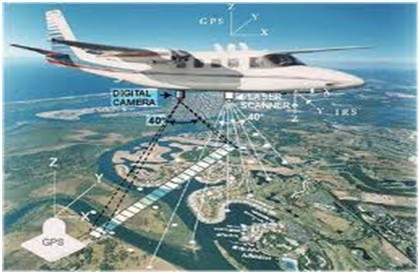
ขั้นตอนสำคัญในการวิเคราะห์ ได้แก่
การสกัดขอบ
การวิเคราะห์และการปรับปรุงขอบประเภทต่างๆ
การส่งและการเข้ารหัส
ภาพแรกที่ถูกส่งผ่านสายไฟคือจากลอนดอนไปนิวยอร์กผ่านเคเบิลใต้น้ำ รูปภาพที่ถูกส่งแสดงด้านล่าง

รูปภาพที่ถูกส่งใช้เวลาสามชั่วโมงในการเข้าถึงจากที่หนึ่งไปยังอีกที่หนึ่ง
ลองนึกภาพดูสิว่าวันนี้เราสามารถดูฟีดวิดีโอสดหรือภาพกล้องวงจรปิดสดจากทวีปหนึ่งไปยังอีกทวีปหนึ่งได้ด้วยความล่าช้าเพียงไม่กี่วินาที หมายความว่ามีการทำงานในสาขานี้มากเกินไป ฟิลด์นี้ไม่ได้เน้นเฉพาะการส่งเท่านั้น แต่ยังรวมถึงการเข้ารหัสด้วย มีการพัฒนารูปแบบต่างๆมากมายสำหรับแบนด์วิดท์สูงหรือต่ำเพื่อเข้ารหัสภาพถ่ายจากนั้นสตรีมผ่านอินเทอร์เน็ตหรืออื่น ๆ
วิสัยทัศน์ของเครื่องจักร / หุ่นยนต์
นอกเหนือจากความท้าทายมากมายที่หุ่นยนต์เผชิญอยู่ในปัจจุบันความท้าทายที่ยิ่งใหญ่ที่สุดอย่างหนึ่งก็คือการเพิ่มวิสัยทัศน์ของหุ่นยนต์ ทำให้หุ่นยนต์สามารถมองเห็นสิ่งต่างๆระบุสิ่งเหล่านั้นระบุสิ่งกีดขวาง ฯลฯ มีงานมากมายที่ได้รับการสนับสนุนจากสาขานี้และได้มีการนำสาขาการมองเห็นคอมพิวเตอร์อื่น ๆ มาใช้ในการทำงานกับมัน
การตรวจจับอุปสรรค์
การตรวจจับสิ่งกีดขวางเป็นหนึ่งในงานทั่วไปที่ทำผ่านการประมวลผลภาพโดยการระบุประเภทของวัตถุต่างๆในภาพจากนั้นคำนวณระยะห่างระหว่างหุ่นยนต์และสิ่งกีดขวาง

หุ่นยนต์สาวกไลน์
หุ่นยนต์ส่วนใหญ่ในปัจจุบันทำงานโดยทำตามเส้นจึงเรียกว่าหุ่นยนต์ผู้ติดตามสาย วิธีนี้ช่วยให้หุ่นยนต์เคลื่อนที่ไปตามเส้นทางและทำงานบางอย่างได้ สิ่งนี้สามารถทำได้โดยการประมวลผลภาพ

การประมวลผลสี
การประมวลผลสีรวมถึงการประมวลผลภาพสีและช่องว่างสีต่างๆที่ใช้ ตัวอย่างเช่นรุ่นสี RGB, YCbCr, HSV นอกจากนี้ยังเกี่ยวข้องกับการศึกษาการส่งการจัดเก็บและการเข้ารหัสภาพสีเหล่านี้
การจดจำรูปแบบ
การจดจำรูปแบบเกี่ยวข้องกับการศึกษาจากการประมวลผลภาพและจากสาขาอื่น ๆ ที่รวมถึงการเรียนรู้ของเครื่อง (สาขาหนึ่งของปัญญาประดิษฐ์) ในการจดจำรูปแบบจะใช้การประมวลผลภาพเพื่อระบุวัตถุในรูปภาพจากนั้นจะใช้การเรียนรู้ของเครื่องเพื่อฝึกระบบสำหรับการเปลี่ยนแปลงรูปแบบ การจดจำรูปแบบใช้ในการวินิจฉัยโดยใช้คอมพิวเตอร์ช่วยการจดจำลายมือการจดจำรูปภาพเป็นต้น
การประมวลผลวิดีโอ
วิดีโอไม่ได้เป็นเพียงแค่การเคลื่อนไหวที่รวดเร็วของรูปภาพเท่านั้น คุณภาพของวิดีโอขึ้นอยู่กับจำนวนเฟรม / รูปภาพต่อนาทีและคุณภาพของแต่ละเฟรมที่ใช้ การประมวลผลวิดีโอเกี่ยวข้องกับการลดสัญญาณรบกวนการเพิ่มรายละเอียดการตรวจจับการเคลื่อนไหวการแปลงอัตราเฟรมการแปลงอัตราส่วนการแปลงพื้นที่สีเป็นต้น
เราจะดูตัวอย่างนี้เพื่อทำความเข้าใจแนวคิดของมิติ
คิดว่าคุณมีเพื่อนที่อาศัยอยู่บนดวงจันทร์และเขาต้องการส่งของขวัญให้คุณเป็นของขวัญวันเกิด เขาถามคุณเกี่ยวกับที่อยู่อาศัยของคุณบนโลก ปัญหาเดียวคือบริการจัดส่งบนดวงจันทร์ไม่เข้าใจที่อยู่ตามตัวอักษร แต่จะเข้าใจเฉพาะพิกัดที่เป็นตัวเลขเท่านั้น แล้วคุณจะส่งตำแหน่งของคุณให้เขาบนโลกได้อย่างไร?
นั่นคือที่มาของแนวคิดเรื่องมิติ มิติกำหนดจำนวนจุดต่ำสุดที่ต้องใช้ในการชี้ตำแหน่งของวัตถุใด ๆ ภายในช่องว่าง
กลับไปที่ตัวอย่างของเราอีกครั้งที่คุณต้องส่งตำแหน่งบนโลกให้เพื่อนบนดวงจันทร์ คุณส่งพิกัดสามคู่ให้เขา อันแรกเรียกว่าลองจิจูดอันที่สองเรียกว่าละติจูดและอันที่สามเรียกว่าระดับความสูง
พิกัดทั้งสามนี้กำหนดตำแหน่งของคุณบนพื้นโลก สองตัวแรกกำหนดตำแหน่งของคุณและอันที่สามกำหนดความสูงของคุณเหนือระดับน้ำทะเล
นั่นหมายความว่าต้องมีเพียงสามพิกัดเท่านั้นที่จะกำหนดตำแหน่งของคุณบนโลกได้ นั่นหมายความว่าคุณอาศัยอยู่ในโลกที่เป็น 3 มิติ และด้วยเหตุนี้จึงไม่เพียงตอบคำถามเกี่ยวกับมิติ แต่ยังตอบเหตุผลว่าทำไมเราจึงอาศัยอยู่ในโลก 3 มิติ
เนื่องจากเรากำลังศึกษาแนวคิดนี้โดยอ้างอิงถึงการประมวลผลภาพดิจิทัลดังนั้นตอนนี้เราจะเชื่อมโยงแนวคิดเรื่องมิตินี้กับรูปภาพ
ขนาดของภาพ
ดังนั้นถ้าเราอยู่ในโลก 3 มิติหมายถึงโลก 3 มิติแล้วขนาดของภาพที่เราจับได้คืออะไร ภาพเป็นสองมิตินั่นคือเหตุผลที่เรากำหนดภาพเป็นสัญญาณ 2 มิติด้วย รูปภาพมีความสูงและความกว้างเท่านั้น ภาพไม่มีความลึก เพียงแค่ดูที่ภาพด้านล่างนี้
หากคุณจะดูรูปด้านบนแสดงว่ามีแกนเพียงสองแกนคือแกนความสูงและความกว้าง คุณไม่สามารถรับรู้ความลึกจากภาพนี้ นั่นคือเหตุผลที่เรากล่าวว่าภาพเป็นสัญญาณสองมิติ แต่ตาของเราสามารถรับรู้วัตถุสามมิติได้ แต่จะมีการอธิบายเพิ่มเติมในบทช่วยสอนถัดไปเกี่ยวกับวิธีการทำงานของกล้องและการรับรู้ภาพ
การสนทนานี้นำไปสู่คำถามอื่น ๆ ว่าระบบ 3 มิติเกิดขึ้นจาก 2 มิติได้อย่างไร
โทรทัศน์ทำงานอย่างไร?
ถ้าเราดูภาพด้านบนเราจะเห็นว่ามันเป็นภาพสองมิติ ในการแปลงเป็นสามมิติเราต้องการมิติอื่น ให้ใช้เวลาเป็นมิติที่สามในกรณีนี้เราจะย้ายภาพสองมิตินี้ในช่วงเวลาของมิติที่สาม แนวคิดเดียวกับที่เกิดขึ้นในโทรทัศน์ซึ่งช่วยให้เรารับรู้ความลึกของวัตถุต่างๆบนหน้าจอ นั่นหมายความว่าสิ่งที่มาในทีวีหรือสิ่งที่เราเห็นในจอโทรทัศน์นั้นเป็น 3d เราสามารถใช่ เหตุผลก็คือในกรณีของทีวีเราถ้าเราเล่นวิดีโอ จากนั้นวิดีโอก็ไม่ใช่สิ่งอื่นใดนอกจากรูปภาพสองมิติจะเคลื่อนไปตามมิติเวลา เนื่องจากวัตถุสองมิติกำลังเคลื่อนผ่านมิติที่สามซึ่งเป็นเวลาดังนั้นเราจึงสามารถพูดได้ว่าเป็น 3 มิติ
ขนาดสัญญาณต่างกัน
สัญญาณ 1 มิติ
ตัวอย่างทั่วไปของสัญญาณ 1 มิติคือรูปคลื่น สามารถแทนค่าทางคณิตศาสตร์เป็น
F (x) = รูปคลื่น
โดยที่ x เป็นตัวแปรอิสระ เนื่องจากเป็นสัญญาณมิติเดียวดังนั้นจึงมีการใช้ตัวแปร x เพียงตัวเดียว
การแสดงภาพของสัญญาณมิติเดียวได้รับด้านล่าง:
รูปด้านบนแสดงสัญญาณมิติเดียว
ตอนนี้นำไปสู่คำถามอื่นซึ่งก็คือแม้ว่ามันจะเป็นสัญญาณมิติเดียวแล้วทำไมมันถึงมีสองแกน? คำตอบสำหรับคำถามนี้คือแม้ว่ามันจะเป็นสัญญาณหนึ่งมิติ แต่เรากำลังวาดมันในพื้นที่สองมิติ หรือเราสามารถพูดได้ว่าช่องว่างที่เราใช้แทนสัญญาณนี้เป็นสองมิติ นั่นเป็นเหตุให้ดูเหมือนสัญญาณสองมิติ
บางทีคุณอาจเข้าใจแนวคิดของมิติเดียวได้ดีขึ้นโดยดูรูปด้านล่าง

ตอนนี้อ้างอิงกลับไปที่การสนทนาครั้งแรกของเราเกี่ยวกับมิติพิจารณารูปด้านบนเป็นเส้นจริงที่มีจำนวนบวกจากจุดหนึ่งไปยังอีกจุดหนึ่ง ทีนี้ถ้าเราต้องอธิบายตำแหน่งของจุดใด ๆ บนเส้นนี้เราก็แค่ต้องการตัวเลขเพียงตัวเดียวซึ่งหมายถึงมิติเดียว
สัญญาณ 2 มิติ
ตัวอย่างทั่วไปของสัญญาณสองมิติคือภาพซึ่งได้กล่าวไปแล้วข้างต้น

ดังที่เราได้เห็นแล้วว่าภาพเป็นสัญญาณสองมิติกล่าวคือมีสองมิติ สามารถแสดงทางคณิตศาสตร์เป็น:
F (x, y) = รูปภาพ
โดยที่ x และ y เป็นสองตัวแปร แนวคิดของสองมิติสามารถอธิบายได้ในแง่ของคณิตศาสตร์เช่น:
ตอนนี้ในรูปด้านบนให้ติดป้ายที่มุมทั้งสี่ของสี่เหลี่ยมเป็น A, B, C และ D ตามลำดับ ถ้าเราเรียกส่วนของเส้นตรงหนึ่งส่วนในรูป AB และอีกแผ่นซีดีเราจะเห็นว่าส่วนคู่ขนานทั้งสองนี้รวมกันและสร้างเป็นกำลังสอง แต่ละส่วนของเส้นตรงสอดคล้องกับมิติเดียวดังนั้นส่วนของเส้นตรงทั้งสองนี้จึงสอดคล้องกับ 2 มิติ
สัญญาณ 3 มิติ
สัญญาณสามมิติตามชื่อหมายถึงสัญญาณที่มีสามมิติ ตัวอย่างที่พบบ่อยที่สุดได้รับการกล่าวถึงในตอนต้นซึ่งเป็นของโลกของเรา เราอาศัยอยู่ในโลกสามมิติ ตัวอย่างนี้ได้รับการกล่าวถึงอย่างละเอียดมาก อีกตัวอย่างหนึ่งของสัญญาณสามมิติคือลูกบาศก์หรือข้อมูลเชิงปริมาตรหรือตัวอย่างที่พบบ่อยที่สุดคือตัวการ์ตูนเคลื่อนไหวหรือ 3 มิติ
การแสดงทางคณิตศาสตร์ของสัญญาณสามมิติคือ:
F (x, y, z) = ตัวละครที่เคลื่อนไหว
แกนหรือมิติอื่น Z เกี่ยวข้องกับสามมิติซึ่งให้ภาพลวงตาของความลึก ในระบบพิกัดคาร์ทีเซียนสามารถดูได้ดังนี้:

สัญญาณ 4 มิติ
ในสัญญาณสี่มิติสี่มิติเกี่ยวข้อง สามตัวแรกเหมือนกับสัญญาณสามมิติคือ (X, Y, Z) และอันที่สี่ที่เพิ่มเข้ามาคือ T (เวลา) เวลามักเรียกว่ามิติชั่วคราวซึ่งเป็นวิธีการวัดการเปลี่ยนแปลง ในทางคณิตศาสตร์สัญญาณสี่ d สามารถระบุได้ดังนี้:
F (x, y, z, t) = ภาพยนตร์การ์ตูน
ตัวอย่างทั่วไปของสัญญาณ 4 มิติอาจเป็นภาพเคลื่อนไหว 3 มิติ เนื่องจากตัวละครแต่ละตัวเป็นตัวละคร 3 มิติและจากนั้นพวกเขาก็เคลื่อนไหวตามเวลาเนื่องจากเราเห็นภาพลวงตาของภาพยนตร์สามมิติเหมือนโลกแห่งความจริงมากขึ้น
นั่นหมายความว่าในความเป็นจริงภาพยนตร์แอนิเมชั่นมี 4 มิติคือการเคลื่อนไหวของตัวละคร 3 มิติในช่วงเวลามิติที่สี่
ดวงตาของมนุษย์ทำงานอย่างไร?
ก่อนที่เราจะพูดถึงการสร้างภาพในกล้องอะนาล็อกและดิจิตอลเราต้องหารือเกี่ยวกับการสร้างภาพบนดวงตาของมนุษย์ก่อน เนื่องจากหลักการพื้นฐานที่ตามมาด้วยกล้องนั้นถูกนำมาจากทางสายตามนุษย์จึงทำงานได้
เมื่อแสงตกกระทบกับวัตถุนั้นแสงจะสะท้อนกลับหลังจากกระทบกับวัตถุนั้น รังสีของแสงเมื่อผ่านเลนส์ตาก่อให้เกิดมุมเฉพาะและภาพจะเกิดขึ้นที่เรตินาซึ่งเป็นด้านหลังของผนัง ภาพที่เกิดขึ้นจะกลับหัว ภาพนี้ถูกตีความโดยสมองและนั่นทำให้เราสามารถเข้าใจสิ่งต่างๆ เนื่องจากการก่อตัวของมุมเราสามารถรับรู้ความสูงและความลึกของวัตถุที่เราเห็นได้ สิ่งนี้ได้รับการอธิบายเพิ่มเติมในบทช่วยสอนเรื่องการเปลี่ยนแปลงมุมมอง
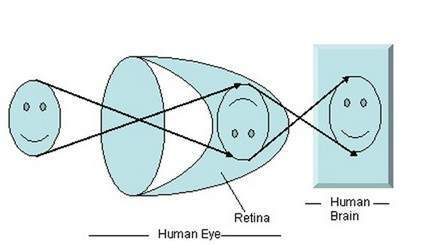
ดังที่คุณเห็นในรูปด้านบนว่าเมื่อแสงดวงอาทิตย์ตกกระทบวัตถุ (ในกรณีนี้คือใบหน้าของวัตถุ) จะสะท้อนกลับและรังสีที่แตกต่างกันจะก่อให้เกิดมุมที่แตกต่างกันเมื่อส่งผ่านเลนส์และภาพกลับด้านของ วัตถุได้ถูกสร้างขึ้นที่ผนังด้านหลัง ส่วนสุดท้ายของรูปแสดงว่าวัตถุได้รับการตีความโดยสมองและกลับด้าน
ตอนนี้เรามาสนทนากันที่รูปแบบภาพในกล้องอนาล็อกและดิจิตอล
การสร้างภาพในกล้องอะนาล็อก
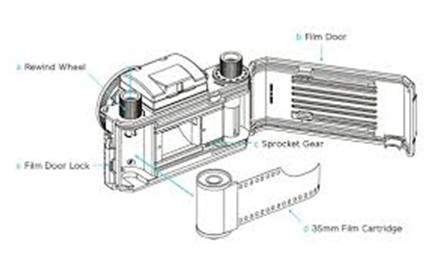
ในกล้องอะนาล็อกการสร้างภาพเกิดจากปฏิกิริยาทางเคมีที่เกิดขึ้นบนแถบที่ใช้ในการสร้างภาพ
ใช้แถบ 35 มม. ในกล้องอะนาล็อก แสดงในรูปด้วยตลับฟิล์ม 35 มม. แถบนี้เคลือบด้วยซิลเวอร์เฮไลด์ (สารเคมี)

ใช้แถบ 35 มม. ในกล้องอะนาล็อก แสดงในรูปด้วยตลับฟิล์ม 35 มม. แถบนี้เคลือบด้วยซิลเวอร์เฮไลด์ (สารเคมี)
แสงไม่ได้เป็นเพียงอนุภาคขนาดเล็กที่เรียกว่าอนุภาคโฟตอนดังนั้นเมื่ออนุภาคโฟตอนเหล่านี้ถูกส่งผ่านกล้องจะทำปฏิกิริยากับอนุภาคซิลเวอร์เฮไลด์บนแถบและส่งผลให้เงินซึ่งเป็นลบของภาพ
เพื่อให้เข้าใจได้ดีขึ้นลองดูสมการนี้
โฟตอน (อนุภาคแสง) + ซิลเวอร์เฮไลด์? สีเงิน? ภาพลบ

นี่เป็นเพียงพื้นฐานเท่านั้นแม้ว่าการสร้างภาพจะเกี่ยวข้องกับแนวคิดอื่น ๆ อีกมากมายเกี่ยวกับการผ่านของแสงภายในและแนวคิดของชัตเตอร์และความเร็วชัตเตอร์และรูรับแสงและการเปิด แต่สำหรับตอนนี้เราจะไปยังส่วนถัดไป แม้ว่าแนวคิดเหล่านี้ส่วนใหญ่จะได้รับการกล่าวถึงในบทแนะนำเรื่องชัตเตอร์และรูรับแสง
นี่เป็นเพียงพื้นฐานเท่านั้นแม้ว่าการสร้างภาพจะเกี่ยวข้องกับแนวคิดอื่น ๆ อีกมากมายเกี่ยวกับการผ่านของแสงภายในและแนวคิดของชัตเตอร์และความเร็วชัตเตอร์และรูรับแสงและการเปิด แต่สำหรับตอนนี้เราจะไปยังส่วนถัดไป แม้ว่าแนวคิดเหล่านี้ส่วนใหญ่จะได้รับการกล่าวถึงในบทแนะนำเรื่องชัตเตอร์และรูรับแสง
การสร้างภาพในกล้องดิจิทัล
ในกล้องดิจิทัลการสร้างภาพไม่ได้เกิดจากปฏิกิริยาทางเคมีที่เกิดขึ้น แต่มันค่อนข้างซับซ้อนกว่านี้ ในกล้องดิจิทัลอาร์เรย์ CCD ใช้สำหรับการสร้างภาพ
การสร้างภาพผ่านอาร์เรย์ CCD

CCD ย่อมาจากอุปกรณ์ชาร์จคู่ เป็นเซ็นเซอร์ภาพและเช่นเดียวกับเซ็นเซอร์อื่น ๆ ที่ตรวจจับค่าและแปลงเป็นสัญญาณไฟฟ้า ในกรณีของ CCD จะตรวจจับภาพและแปลงเป็นสัญญาณไฟฟ้าเป็นต้น
CCD นี้อยู่ในรูปของอาร์เรย์หรือตารางสี่เหลี่ยม มันเหมือนกับเมทริกซ์ที่เซลล์แต่ละเซลล์ในเมทริกซ์มีเซ็นเซอร์ที่ตรวจจับความเข้มของโฟตอน
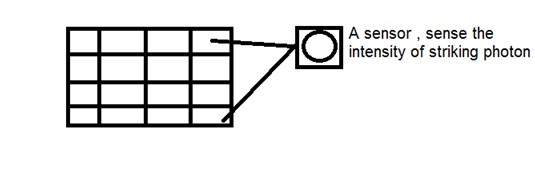
เช่นเดียวกับกล้องอะนาล็อกในกรณีของดิจิตอลเช่นกันเมื่อแสงตกกระทบวัตถุแสงจะสะท้อนกลับหลังจากกระทบวัตถุและอนุญาตให้เข้าไปในกล้องได้
เซ็นเซอร์แต่ละตัวของอาร์เรย์ CCD นั้นเป็นเซ็นเซอร์อนาล็อก เมื่อโฟตอนของแสงกระทบกับชิปจะมีประจุไฟฟ้าเพียงเล็กน้อยในเซ็นเซอร์ภาพถ่ายแต่ละตัว การตอบสนองของเซ็นเซอร์แต่ละตัวจะเท่ากับปริมาณแสงหรือพลังงาน (โฟตอน) ที่ขีดทับบนพื้นผิวของเซ็นเซอร์โดยตรง
เนื่องจากเราได้กำหนดภาพเป็นสัญญาณสองมิติแล้วและเนื่องจากการก่อตัวของอาร์เรย์ CCD สองมิติภาพที่สมบูรณ์จึงสามารถทำได้จากอาร์เรย์ CCD นี้
มีเซ็นเซอร์จำนวน จำกัด และหมายความว่าสามารถจับรายละเอียดได้อย่าง จำกัด นอกจากนี้เซ็นเซอร์แต่ละตัวยังสามารถมีค่าเดียวกับอนุภาคโฟตอนแต่ละตัวที่กระทบกับมัน
ดังนั้นจำนวนโฟตอนที่โดดเด่น (ปัจจุบัน) จึงถูกนับและจัดเก็บ เพื่อที่จะวัดสิ่งเหล่านี้ได้อย่างแม่นยำเซนเซอร์ CMOS ภายนอกจะติดมากับอาร์เรย์ CCD ด้วย
รู้เบื้องต้นเกี่ยวกับพิกเซล
ค่าของเซ็นเซอร์แต่ละตัวของอาร์เรย์ CCD หมายถึงค่าของแต่ละพิกเซล จำนวนเซ็นเซอร์ = จำนวนพิกเซล นอกจากนี้ยังหมายความว่าเซ็นเซอร์แต่ละตัวสามารถมีได้เพียงค่าเดียวเท่านั้น
กำลังจัดเก็บภาพ
ประจุที่จัดเก็บโดยอาร์เรย์ CCD จะถูกแปลงเป็นแรงดันไฟฟ้าทีละพิกเซล ด้วยความช่วยเหลือของวงจรเพิ่มเติมแรงดันไฟฟ้านี้จะถูกแปลงเป็นข้อมูลดิจิทัลจากนั้นจะถูกเก็บไว้
แต่ละ บริษัท ที่ผลิตกล้องดิจิทัลจะทำเซ็นเซอร์ CCD ของตัวเอง ซึ่งรวมถึง Sony, Mistubishi, Nikon, Samsung, Toshiba, FujiFilm, Canon เป็นต้น
นอกเหนือจากปัจจัยอื่น ๆ แล้วคุณภาพของภาพที่ถ่ายยังขึ้นอยู่กับประเภทและคุณภาพของอาร์เรย์ CCD ที่ใช้
ในบทช่วยสอนนี้เราจะพูดถึงแนวคิดพื้นฐานเกี่ยวกับกล้องเช่นรูรับแสงชัตเตอร์ความเร็วชัตเตอร์ ISO และเราจะพูดถึงการใช้แนวคิดเหล่านี้ร่วมกันเพื่อถ่ายภาพที่ดี
รูรับแสง
รูรับแสงคือช่องเล็ก ๆ ที่ช่วยให้แสงเดินทางเข้าไปในกล้องได้ นี่คือภาพของรูรับแสง

คุณจะเห็นใบมีดเล็ก ๆ เหมือนสิ่งของอยู่ในรูรับแสง ใบมีดเหล่านี้สร้างรูปทรงแปดเหลี่ยมที่สามารถเปิดปิดได้ ดังนั้นจึงสมเหตุสมผลที่ยิ่งใบพัดจะเปิดมากขึ้นช่องที่แสงจะต้องผ่านก็จะใหญ่ขึ้น ยิ่งรูใหญ่เท่าไหร่แสงก็ยิ่งเข้าได้มากขึ้นเท่านั้น
ผลกระทบ
เอฟเฟกต์ของรูรับแสงจะสัมพันธ์โดยตรงกับความสว่างและความมืดของภาพ หากช่องรับแสงกว้างก็จะทำให้แสงผ่านเข้าสู่กล้องได้มากขึ้น แสงที่มากขึ้นจะส่งผลให้มีโฟตอนมากขึ้นซึ่งจะส่งผลให้ภาพสว่างขึ้นในที่สุด
ตัวอย่างนี้แสดงไว้ด้านล่าง
พิจารณาภาพถ่ายสองภาพนี้


ด้านขวาจะดูสว่างกว่านั่นหมายความว่าเมื่อถ่ายด้วยกล้องรูรับแสงจะเปิดกว้าง เมื่อเปรียบเทียบกับภาพอื่นทางด้านซ้ายซึ่งมืดมากเมื่อเทียบกับภาพแรกนั่นแสดงให้เห็นว่าเมื่อถ่ายภาพนั้นรูรับแสงไม่ได้เปิดกว้าง
ขนาด
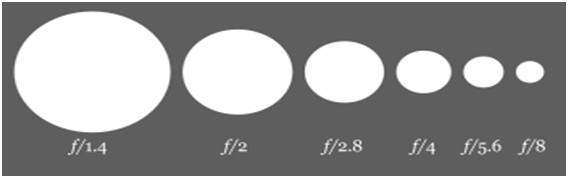
ตอนนี้ให้พูดคุยเกี่ยวกับคณิตศาสตร์ที่อยู่เบื้องหลังรูรับแสง ขนาดของรูรับแสงแสดงด้วยค่า af และมันแปรผกผันกับการเปิดรูรับแสง
นี่คือสองสมการที่อธิบายแนวคิดนี้ได้ดีที่สุด
ขนาดรูรับแสงกว้าง = ค่า f เล็ก
ขนาดรูรับแสงเล็ก = ค่า f มากกว่า
ในภาพสามารถแสดงเป็น:
ชัตเตอร์
หลังจากรูรับแสงแล้วจะมีชัตเตอร์ แสงเมื่อปล่อยให้ผ่านจากรูรับแสงจะตกกระทบกับชัตเตอร์โดยตรง ชัตเตอร์คือฝาปิดหน้าต่างที่ปิดสนิทหรืออาจคิดว่าเป็นม่านก็ได้ โปรดจำไว้ว่าเมื่อเราพูดถึงเซ็นเซอร์ CCD อาร์เรย์ที่สร้างภาพ ด้านหลังชัตเตอร์คือเซ็นเซอร์ ชัตเตอร์จึงเป็นเพียงสิ่งเดียวที่อยู่ระหว่างการสร้างภาพและแสงเมื่อผ่านรูรับแสง
ทันทีที่ชัตเตอร์เปิดขึ้นแสงจะตกที่เซ็นเซอร์ภาพและภาพจะเกิดขึ้นบนอาร์เรย์
ผลกระทบ
หากชัตเตอร์ปล่อยให้แสงผ่านไปนานกว่านี้ภาพจะสว่างขึ้น ในทำนองเดียวกันภาพที่มืดกว่าจะเกิดขึ้นเมื่อชัตเตอร์ได้รับอนุญาตให้เคลื่อนที่อย่างรวดเร็วดังนั้นแสงที่อนุญาตให้ผ่านจึงมีโฟตอนน้อยมากและภาพที่เกิดขึ้นบนเซ็นเซอร์อาร์เรย์ CCD จะมืดมาก
ชัตเตอร์มีแนวคิดหลักอีกสองประการ:
ความเร็วชัตเตอร์
เวลาชัตเตอร์
ความเร็วชัตเตอร์
ความเร็วชัตเตอร์สามารถเรียกได้ว่าเป็นจำนวนครั้งที่ชัตเตอร์เปิดหรือปิด จำไว้ว่าเราไม่ได้พูดถึงระยะเวลาที่ชัตเตอร์เปิดหรือปิด
เวลาชัตเตอร์
เวลาชัตเตอร์สามารถกำหนดเป็น
เมื่อชัตเตอร์เปิดขึ้นระยะเวลารอจนกว่าจะปิดเรียกว่าเวลาชัตเตอร์
ในกรณีนี้เราไม่ได้พูดถึงกี่ครั้งที่ชัตเตอร์เปิดหรือปิด แต่เรากำลังพูดถึงเวลาที่ยังคงเปิดกว้าง
ตัวอย่างเช่น:
เราสามารถเข้าใจแนวคิดทั้งสองนี้ได้ดีขึ้นด้วยวิธีนี้ นั่นหมายความว่าชัตเตอร์จะเปิด 15 ครั้งแล้วจึงปิดและแต่ละครั้งจะเปิดเป็นเวลา 1 วินาทีแล้วจึงปิด ในตัวอย่างนี้ 15 คือความเร็วชัตเตอร์และ 1 วินาทีคือเวลาชัตเตอร์
ความสัมพันธ์
ความสัมพันธ์ระหว่างความเร็วชัตเตอร์และเวลาชัตเตอร์คือทั้งคู่มีสัดส่วนผกผันซึ่งกันและกัน
ความสัมพันธ์นี้สามารถกำหนดได้ในสมการด้านล่าง
ความเร็วชัตเตอร์มากขึ้น = เวลาชัตเตอร์น้อยลง
ความเร็วชัตเตอร์น้อยลง = เวลาชัตเตอร์มากขึ้น
คำอธิบาย:
ยิ่งใช้เวลาน้อยเท่าไหร่ความเร็วก็ยิ่งมากขึ้นเท่านั้น และยิ่งต้องใช้เวลามากเท่าไหร่ความเร็วก็ยิ่งน้อยลงเท่านั้น
การใช้งาน
ทั้งสองแนวคิดร่วมกันทำให้เกิดการใช้งานที่หลากหลาย บางส่วนได้รับด้านล่าง
วัตถุที่เคลื่อนไหวเร็ว:
หากคุณต้องการถ่ายภาพของวัตถุที่เคลื่อนที่เร็วอาจเป็นรถยนต์หรืออะไรก็ได้ การปรับความเร็วชัตเตอร์และเวลาจะมีผลอย่างมาก
ดังนั้นในการจับภาพเช่นนี้เราจะทำการแก้ไขสองครั้ง:
เพิ่มความเร็วชัตเตอร์
ลดเวลาชัตเตอร์
สิ่งที่เกิดขึ้นคือเมื่อเราเพิ่มความเร็วชัตเตอร์จำนวนครั้งมากขึ้นชัตเตอร์จะเปิดหรือปิด หมายความว่าตัวอย่างแสงที่แตกต่างกันจะยอมให้ผ่านเข้ามาได้และเมื่อเราลดเวลาชัตเตอร์ลงนั่นหมายความว่าเราจะจับภาพฉากนั้นทันทีและปิดประตูชัตเตอร์
หากคุณทำเช่นนี้คุณจะได้ภาพที่คมชัดของวัตถุที่เคลื่อนไหวเร็ว
เพื่อที่จะเข้าใจเราจะดูตัวอย่างนี้ สมมติว่าคุณต้องการถ่ายภาพการตกน้ำที่เคลื่อนไหวอย่างรวดเร็ว
คุณตั้งค่าความเร็วชัตเตอร์เป็น 1 วินาทีและคุณถ่ายภาพ นี่คือสิ่งที่คุณจะได้รับ

จากนั้นตั้งค่าความเร็วชัตเตอร์ให้เร็วขึ้นเท่านี้คุณก็จะได้

จากนั้นอีกครั้งคุณตั้งค่าความเร็วชัตเตอร์ให้เร็วยิ่งขึ้นและคุณจะได้รับ

คุณจะเห็นในภาพสุดท้ายว่าเราเพิ่มความเร็วชัตเตอร์ให้เร็วมากนั่นหมายความว่าชัตเตอร์จะเปิดหรือปิดใน 200 วินาที 1 วินาทีและเราได้ภาพที่คมชัด
ISO
ค่า ISO ถูกวัดเป็นตัวเลข หมายถึงความไวของแสงต่อกล้อง หากค่า ISO ต่ำลงหมายความว่ากล้องของเรามีความไวต่อแสงน้อยลงและหากค่า ISO สูงแสดงว่ามีความไวแสงมากกว่า
ผลกระทบ
ยิ่ง ISO สูงเท่าไหร่ภาพก็จะยิ่งสว่างมากขึ้นเท่านั้น หากตั้งค่า ISO ไว้ที่ 1600 ภาพจะสว่างขึ้นมากและในทางกลับกัน
ผลข้างเคียง
หาก ISO เพิ่มขึ้นสัญญาณรบกวนในภาพจะเพิ่มขึ้นด้วย ปัจจุบัน บริษัท ผลิตกล้องส่วนใหญ่กำลังดำเนินการลบสัญญาณรบกวนออกจากภาพเมื่อตั้งค่า ISO ไว้ที่ความเร็วสูงขึ้น
พิกเซล
พิกเซลเป็นองค์ประกอบที่เล็กที่สุดของรูปภาพ แต่ละพิกเซลสอดคล้องกับค่าใดค่าหนึ่ง ในภาพขนาด 8 บิตสีเทาค่าของพิกเซลระหว่าง 0 ถึง 255 ค่าของพิกเซลที่จุดใด ๆ จะสอดคล้องกับความเข้มของโฟตอนแสงที่ตกกระทบ ณ จุดนั้น แต่ละพิกเซลจะจัดเก็บค่าตามสัดส่วนของความเข้มของแสง ณ ตำแหน่งนั้น ๆ
PEL
พิกเซลเรียกอีกอย่างว่า PEL คุณสามารถเข้าใจพิกเซลได้มากขึ้นจากรูปภาพด้านล่าง
ในภาพด้านบนอาจมีพิกเซลหลายพันพิกเซลซึ่งประกอบกันเป็นภาพนี้ เราจะซูมภาพนั้นให้เท่าที่จะเห็นการแบ่งพิกเซลบางส่วน ดังแสดงในภาพด้านล่าง

ในภาพด้านบนอาจมีพิกเซลหลายพันพิกเซลซึ่งประกอบกันเป็นภาพนี้ เราจะซูมภาพนั้นให้เท่าที่จะเห็นการแบ่งพิกเซลบางส่วน ดังแสดงในภาพด้านล่าง
ความสัมพันธ์จัดส่งด้วยอาร์เรย์ CCD
เราได้เห็นแล้วว่าภาพเกิดขึ้นในอาร์เรย์ CCD ได้อย่างไร ดังนั้นพิกเซลจึงสามารถกำหนดเป็น
การแบ่งอาร์เรย์ CCD ที่เล็กที่สุดเรียกอีกอย่างว่าพิกเซล
แต่ละส่วนของอาร์เรย์ CCD มีค่าเทียบกับความเข้มของโฟตอนที่กระทบกับมัน ค่านี้สามารถเรียกได้ว่าเป็นพิกเซล
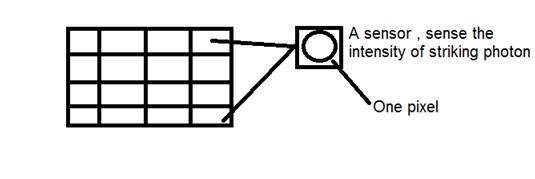
การคำนวณจำนวนพิกเซลทั้งหมด
เราได้กำหนดภาพเป็นสัญญาณสองมิติหรือเมทริกซ์ จากนั้นในกรณีนั้นจำนวน PEL จะเท่ากับจำนวนแถวที่คูณด้วยจำนวนคอลัมน์
สิ่งนี้สามารถแสดงทางคณิตศาสตร์ได้ดังนี้:
จำนวนพิกเซลทั้งหมด = จำนวนแถว (X) จำนวนคอลัมน์
หรือเราสามารถพูดได้ว่าจำนวนคู่พิกัด (x, y) ประกอบขึ้นเป็นจำนวนพิกเซลทั้งหมด
เราจะดูรายละเอียดเพิ่มเติมในบทช่วยสอนเกี่ยวกับประเภทรูปภาพว่าเราจะคำนวณพิกเซลในภาพสีได้อย่างไร
ระดับสีเทา
ค่าของพิกเซล ณ จุดใด ๆ แสดงถึงความเข้มของภาพ ณ ตำแหน่งนั้นและเรียกอีกอย่างว่าระดับสีเทา
เราจะดูรายละเอียดเพิ่มเติมเกี่ยวกับค่าของพิกเซลในการจัดเก็บภาพและแบบฝึกหัดบิตต่อพิกเซล แต่สำหรับตอนนี้เราจะดูแนวคิดของค่าพิกเซลเพียงค่าเดียว
ค่าพิกเซล (0)
ดังที่ได้กำหนดไว้แล้วในตอนต้นของบทช่วยสอนนี้ว่าแต่ละพิกเซลสามารถมีได้เพียงค่าเดียวและแต่ละค่าจะแสดงถึงความเข้มของแสงที่จุดนั้นของภาพ
ตอนนี้เราจะดูที่ค่าเฉพาะ 0 ค่า 0 หมายถึงไม่มีแสง หมายความว่า 0 หมายถึงความมืดและยังหมายความว่าเมื่อใดก็ตามที่พิกเซลมีค่าเป็น 0 หมายความว่า ณ จุดนั้นจะเกิดสีดำขึ้น
ลองดูที่เมทริกซ์รูปภาพนี้
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
ตอนนี้เมทริกซ์รูปภาพนี้เต็มไปด้วย 0 พิกเซลทั้งหมดมีค่าเป็น 0 ถ้าเราจะคำนวณจำนวนพิกเซลทั้งหมดจากเมทริกซ์นี้นี่คือวิธีที่เราจะทำ
จำนวนพิกเซลทั้งหมด = จำนวนทั้งหมด ของแถว X ทั้งหมดไม่ ของคอลัมน์
= 3 X 3
= 9.
หมายความว่ารูปภาพจะถูกสร้างขึ้นโดยมี 9 พิกเซลและรูปภาพนั้นจะมีขนาด 3 แถวและ 3 คอลัมน์และที่สำคัญที่สุดคือรูปภาพจะเป็นสีดำ
ภาพที่ได้จะเป็นแบบนี้

ทำไมภาพนี้ถึงเป็นสีดำทั้งหมด เนื่องจากพิกเซลทั้งหมดในภาพมีค่าเป็น 0
เมื่อดวงตาของมนุษย์มองเห็นสิ่งใกล้ตัวจะดูใหญ่กว่าเมื่อเปรียบเทียบกับคนที่อยู่ห่างไกล สิ่งนี้เรียกว่ามุมมองโดยทั่วไป ในขณะที่การแปลงเป็นการถ่ายโอนวัตถุ ฯลฯ จากสถานะหนึ่งไปยังอีกสถานะหนึ่ง
โดยรวมแล้วการแปลงมุมมองจะเกี่ยวข้องกับการแปลงโลก 3 มิติให้เป็นภาพ 2 มิติ หลักการเดียวกันกับที่การมองเห็นของมนุษย์ทำงานและหลักการเดียวกันกับที่กล้องทำงาน
เราจะดูรายละเอียดเกี่ยวกับสาเหตุที่สิ่งนี้เกิดขึ้นว่าวัตถุที่อยู่ใกล้คุณดูใหญ่ขึ้นในขณะที่วัตถุที่อยู่ห่างไกลจะดูเล็กลงแม้ว่าจะดูใหญ่ขึ้นเมื่อคุณเอื้อมถึงก็ตาม
เราจะเริ่มการสนทนานี้โดยใช้กรอบอ้างอิง:
กรอบอ้างอิง:
กรอบอ้างอิงเป็นชุดของค่าที่เกี่ยวข้องกับการที่เราวัดบางสิ่ง
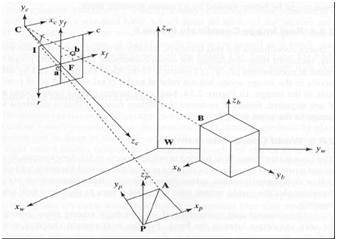
5 เฟรมอ้างอิง
ในการวิเคราะห์โลก 3 มิติ / ภาพ / ฉากจำเป็นต้องมีกรอบอ้างอิง 5 แบบ
Object
World
Camera
Image
Pixel
กรอบพิกัดวัตถุ
เฟรมพิกัดวัตถุใช้สำหรับการสร้างโมเดลวัตถุ ตัวอย่างเช่นการตรวจสอบว่าวัตถุหนึ่ง ๆ อยู่ในสถานที่ที่เหมาะสมหรือไม่เมื่อเทียบกับวัตถุอื่น เป็นระบบพิกัด 3 มิติ
กรอบพิกัดโลก
กรอบพิกัดโลกใช้สำหรับวัตถุที่เกี่ยวข้องร่วมกันในโลก 3 มิติ เป็นระบบพิกัด 3 มิติ
กรอบพิกัดของกล้อง
เฟรมประสานกล้องใช้เพื่อเชื่อมโยงวัตถุที่เกี่ยวข้องกับกล้อง เป็นระบบพิกัด 3 มิติ
กรอบพิกัดภาพ
ไม่ใช่ระบบพิกัด 3 มิติ แต่เป็นระบบ 2d ใช้เพื่ออธิบายวิธีการแมปจุด 3 มิติในระนาบภาพ 2 มิติ
กรอบพิกัดพิกเซล
นอกจากนี้ยังเป็นระบบพิกัด 2d แต่ละพิกเซลมีค่าพิกัดพิกเซล
การเปลี่ยนแปลงระหว่าง 5 เฟรมนี้

นั่นคือวิธีที่ฉาก 3 มิติเปลี่ยนเป็น 2 มิติด้วยภาพพิกเซล
ตอนนี้เราจะอธิบายแนวคิดนี้ทางคณิตศาสตร์
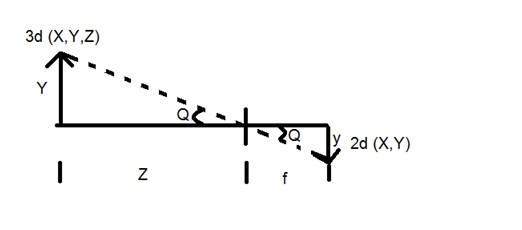
Y = วัตถุ 3 มิติ
y = 2d รูปภาพ
f = ทางยาวโฟกัสของกล้อง
Z = ระยะห่างระหว่างภาพและกล้อง
ตอนนี้มีสองมุมที่แตกต่างกันที่เกิดขึ้นในการแปลงนี้ซึ่งแสดงโดย Q
มุมแรกคือ
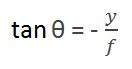
โดยที่เครื่องหมายลบหมายถึงภาพนั้นกลับด้าน มุมที่สองที่เกิดขึ้นคือ:

การเปรียบเทียบทั้งสองสมการที่เราได้รับ

จากสมการนี้เราจะเห็นว่าเมื่อรังสีของแสงสะท้อนกลับหลังจากที่ตกกระทบจากวัตถุผ่านจากกล้องจะเกิดภาพกลับด้าน
เราสามารถเข้าใจสิ่งนี้ได้ดีขึ้นด้วยตัวอย่างนี้
ตัวอย่างเช่น
การคำนวณขนาดของภาพที่เกิดขึ้น
สมมติว่ามีการถ่ายภาพบุคคลสูง 5 ม. และยืนอยู่ห่างจากกล้อง 50 ม. และเราต้องบอกให้ได้ว่าภาพบุคคลนั้นมีขนาดเท่าใดโดยกล้องทางยาวโฟกัสคือ 50 มม.
วิธีการแก้:
เนื่องจากทางยาวโฟกัสมีหน่วยเป็นมิลลิเมตรดังนั้นเราจึงต้องแปลงทุกสิ่งเป็นมิลลิเมตรเพื่อคำนวณ
ดังนั้น,
Y = 5000 มม.
f = 50 มม.
Z = 50000 มม.
เราได้รับการใส่ค่าในสูตร
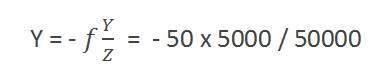
= -5 มม.
อีกครั้งเครื่องหมายลบแสดงว่าภาพกลับด้าน
Bpp หรือบิตต่อพิกเซลแสดงถึงจำนวนบิตต่อพิกเซล จำนวนสีที่แตกต่างกันในภาพขึ้นอยู่กับความลึกของสีหรือบิตต่อพิกเซล
บิตในคณิตศาสตร์:
มันเหมือนกับการเล่นกับบิตไบนารี
หนึ่งบิตสามารถแทนค่าได้กี่ตัวเลข
0
1
สามารถสร้างชุดค่าผสมสองบิตได้กี่ชุด
00
01
10
11
หากเราคิดค้นสูตรคำนวณจำนวนชุดค่าผสมทั้งหมดที่สามารถสร้างจากบิตได้ก็จะเป็นเช่นนี้
โดย bpp หมายถึงบิตต่อพิกเซล ใส่ 1 ในสูตรที่คุณได้ 2 ใส่ 2 ในสูตรคุณจะได้ 4 มันจะเพิ่มขึ้นแบบทวีคูณ
จำนวนสีที่ต่างกัน:
ดังที่เราได้กล่าวไปแล้วในตอนต้นว่าจำนวนสีที่แตกต่างกันนั้นขึ้นอยู่กับจำนวนบิตต่อพิกเซล
ตารางสำหรับบิตและสีบางส่วนได้รับด้านล่าง
| บิตต่อพิกเซล | จำนวนสี |
|---|---|
| 1 bpp | 2 สี |
| 2 bpp | 4 สี |
| 3 bpp | 8 สี |
| 4 bpp | 16 สี |
| 5 bpp | 32 สี |
| 6 bpp | 64 สี |
| 7 bpp | 128 สี |
| 8 bpp | 256 สี |
| 10 bpp | 1024 สี |
| 16 bpp | 65536 สี |
| 24 bpp | 16777216 สี (16.7 ล้านสี) |
| 32 bpp | 4294967296 สี (4294 ล้านสี) |
ตารางนี้แสดงจำนวนบิตต่อพิกเซลและจำนวนสีที่แตกต่างกัน
เฉดสี
คุณสามารถสังเกตเห็นรูปแบบของการเติบโตแบบยกกำลังได้อย่างง่ายดาย ภาพสเกลสีเทาที่มีชื่อเสียงมีขนาด 8 bpp หมายความว่ามีสีที่แตกต่างกัน 256 สีหรือ 256 เฉดสี
เฉดสีสามารถแสดงเป็น:
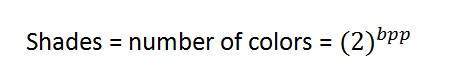
ภาพสีมักอยู่ในรูปแบบ 24 bpp หรือ 16 bpp
เราจะดูเพิ่มเติมเกี่ยวกับรูปแบบสีและประเภทรูปภาพอื่น ๆ ในบทแนะนำเกี่ยวกับประเภทรูปภาพ
ค่าสี:
สีดำ:
สีขาว:
ค่าที่แสดงถึงสีขาวสามารถคำนวณได้ดังนี้:
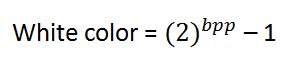
ในกรณีของ 1 bpp, 0 หมายถึงสีดำและ 1 หมายถึงสีขาว
ในกรณีที่ 8 bpp, 0 หมายถึงสีดำและ 255 หมายถึงสีขาว
สีเทา:
เมื่อคุณคำนวณค่าสีขาวดำคุณจะคำนวณค่าพิกเซลของสีเทาได้
สีเทาเป็นจุดกึ่งกลางของสีดำและสีขาว ที่กล่าวว่า
ในกรณีของ 8bpp ค่าพิกเซลที่แสดงถึงสีเทาคือ 127 หรือ 128bpp (ถ้าคุณนับจาก 1 ไม่ใช่จาก 0)
ข้อกำหนดในการจัดเก็บรูปภาพ
หลังจากการอภิปรายของบิตต่อพิกเซลตอนนี้เรามีทุกสิ่งที่เราต้องการในการคำนวณขนาดของภาพ
ขนาดรูปภาพ
ขนาดของรูปภาพขึ้นอยู่กับสามสิ่ง
จำนวนแถว
จำนวนคอลัมน์
จำนวนบิตต่อพิกเซล
สูตรคำนวณขนาดได้รับด้านล่าง
ขนาดของรูปภาพ = แถว * cols * bpp
หมายความว่าถ้าคุณมีภาพให้พูดว่า:

สมมติว่ามี 1024 แถวและมี 1024 คอลัมน์ และเนื่องจากเป็นภาพระดับสีเทาจึงมีเฉดสีเทาที่แตกต่างกัน 256 เฉดหรือมีบิตต่อพิกเซล จากนั้นใส่ค่าเหล่านี้ในสูตรเราจะได้
ขนาดของรูปภาพ = แถว * cols * bpp
= 1024 * 1024 * 8
= 8388608 บิต
แต่เนื่องจากไม่ใช่คำตอบมาตรฐานที่เรารู้จักดังนั้นจะแปลงเป็นรูปแบบของเรา
การแปลงเป็นไบต์ = 8388608/8 = 1048576 ไบต์
การแปลงเป็นกิโลไบต์ = 1048576/1024 = 1024kb
การแปลงเป็นเมกะไบต์ = 1024/1024 = 1 Mb.
นั่นคือวิธีคำนวณขนาดภาพและจัดเก็บ ตอนนี้ในสูตรถ้าคุณได้รับขนาดของภาพและบิตต่อพิกเซลคุณยังสามารถคำนวณแถวและคอลัมน์ของรูปภาพได้โดยที่รูปภาพเป็นรูปสี่เหลี่ยมจัตุรัส (แถวเดียวกันและคอลัมน์เดียวกัน)
มีรูปภาพหลายประเภทและเราจะดูรายละเอียดเกี่ยวกับรูปภาพประเภทต่างๆและการกระจายของสี
ภาพไบนารี
ภาพไบนารีตามชื่อมีค่าพิกเซลเพียงสองค่า
0 และ 1.
ในแบบฝึกหัดบิตต่อพิกเซลก่อนหน้านี้เราได้อธิบายรายละเอียดเกี่ยวกับการแสดงค่าพิกเซลเป็นสีตามลำดับ
ในที่นี้ 0 หมายถึงสีดำและ 1 หมายถึงสีขาว เป็นที่รู้จักกันในชื่อ Monochrome
ภาพขาวดำ:
ภาพที่เกิดขึ้นจึงประกอบด้วยสีดำและสีขาวเท่านั้นจึงสามารถเรียกได้ว่าเป็นภาพขาวดำ

ไม่มีระดับสีเทา
หนึ่งในสิ่งที่น่าสนใจเกี่ยวกับภาพไบนารีนี้คือไม่มีระดับสีเทาอยู่ในนั้น พบเพียงสองสีที่เป็นสีดำและสีขาว
รูปแบบ
ภาพไบนารีมีรูปแบบ PBM (แผนที่บิตแบบพกพา)
รูปแบบสี 2, 3, 4, 5, 6 บิต
ภาพที่มีรูปแบบสี 2, 3, 4, 5 และ 6 บิตยังไม่ถูกใช้อย่างแพร่หลายในปัจจุบัน พวกเขาถูกใช้ในสมัยก่อนสำหรับจอทีวีแบบเก่าหรือจอมอนิเตอร์
แต่แต่ละสีเหล่านี้มีระดับสีเทามากกว่าสองระดับและด้วยเหตุนี้จึงมีสีเทาซึ่งแตกต่างจากภาพไบนารี
ใน 2 บิต 4 ใน 3 บิต 8 ใน 4 บิต 16 ใน 5 บิต 32 ใน 6 บิต 64 สีที่แตกต่างกันมีอยู่
รูปแบบสี 8 บิต
รูปแบบสี 8 บิตเป็นรูปแบบภาพที่มีชื่อเสียงที่สุดรูปแบบหนึ่ง มีเฉดสีที่แตกต่างกันถึง 256 เฉดสี เป็นที่รู้จักกันทั่วไปในชื่อภาพระดับสีเทา
ช่วงของสีใน 8 บิตแตกต่างกันไปตั้งแต่ 0-255 โดย 0 หมายถึงสีดำและ 255 หมายถึงสีขาวและ 127 หมายถึงสีเทา
รูปแบบนี้เริ่มใช้โดยระบบปฏิบัติการ UNIX รุ่นแรก ๆ และ Macintoshes สีรุ่นแรก ๆ
ภาพสีเทาของไอน์สไตน์แสดงอยู่ด้านล่าง:

รูปแบบ
รูปแบบของภาพเหล่านี้คือ PGM (Portable Gray Map)
รูปแบบนี้ไม่ได้รับการสนับสนุนโดยค่าเริ่มต้นจาก windows ในการดูภาพระดับสีเทาคุณต้องมีโปรแกรมดูรูปภาพหรือกล่องเครื่องมือประมวลผลภาพเช่น Matlab
ด้านหลังภาพสเกลสีเทา:
ดังที่เราได้อธิบายไปแล้วหลายครั้งในบทช่วยสอนก่อนหน้านี้ว่ารูปภาพไม่ใช่อะไรนอกจากฟังก์ชันสองมิติและสามารถแสดงด้วยอาร์เรย์หรือเมทริกซ์สองมิติได้ ดังนั้นในกรณีของภาพของไอน์สไตน์ที่แสดงด้านบนจะมีเมทริกซ์สองมิติอยู่ด้านหลังโดยมีค่าอยู่ระหว่าง 0 ถึง 255
แต่นั่นไม่ใช่กรณีของภาพสี
รูปแบบสี 16 บิต
เป็นรูปแบบภาพสี มีสีที่แตกต่างกัน 65,536 สี เรียกอีกอย่างว่ารูปแบบสีสูง
Microsoft ใช้ในระบบที่รองรับรูปแบบสี 8 บิตมากกว่า ตอนนี้ในรูปแบบ 16 บิตนี้และรูปแบบต่อไปเราจะพูดถึงซึ่งเป็นรูปแบบ 24 บิตเป็นทั้งรูปแบบสี
การกระจายของสีในภาพสีไม่ง่ายเหมือนในภาพสีเทา
รูปแบบ 16 บิตจริง ๆ แล้วแบ่งออกเป็นสามรูปแบบเพิ่มเติม ได้แก่ แดงเขียวและน้ำเงิน รูปแบบ (RGB) ที่มีชื่อเสียง
เป็นภาพที่แสดงในภาพด้านล่าง
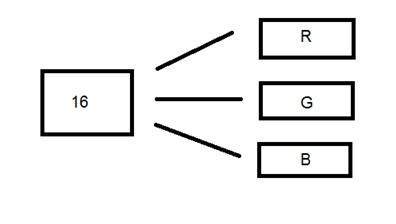
ตอนนี้คำถามเกิดขึ้นว่าคุณจะแบ่ง 16 เป็นสามได้อย่างไร ถ้าคุณทำแบบนี้
5 บิตสำหรับ R, 5 บิตสำหรับ G, 5 บิตสำหรับ B
จากนั้นมีหนึ่งบิตที่เหลืออยู่ในท้ายที่สุด
ดังนั้นการกระจาย 16 บิตจึงเป็นแบบนี้
5 บิตสำหรับ R, 6 บิตสำหรับ G, 5 บิตสำหรับบี
บิตเพิ่มเติมที่ถูกทิ้งไว้จะถูกเพิ่มเข้าไปในบิตสีเขียว เนื่องจากสีเขียวเป็นสีที่สบายตาที่สุดในทั้งสามสีนี้
โปรดทราบว่านี่คือการแจกจ่ายไม่ได้เป็นไปตามระบบทั้งหมด มีบางคนแนะนำช่องอัลฟาใน 16 บิต
การแจกแจงอีกรูปแบบ 16 บิตเป็นดังนี้:
4 บิตสำหรับ R, 4 บิตสำหรับ G, 4 บิตสำหรับ B, 4 บิตสำหรับช่องอัลฟา
หรือบางส่วนแจกจ่ายแบบนี้
5 บิตสำหรับ R, 5 บิตสำหรับ G, 5 บิตสำหรับ B, 1 บิตสำหรับช่องอัลฟา
รูปแบบสี 24 บิต
รูปแบบสี 24 บิตหรือที่เรียกว่ารูปแบบสีจริง เช่นเดียวกับรูปแบบสี 16 บิตในรูปแบบสี 24 บิต 24 บิตจะถูกแจกจ่ายอีกครั้งในสามรูปแบบที่แตกต่างกันคือสีแดงสีเขียวและสีน้ำเงิน
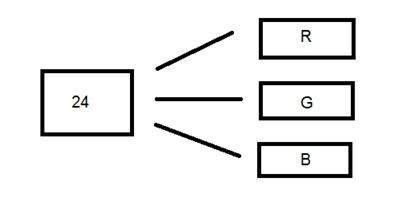
เนื่องจาก 24 ถูกหารด้วย 8 เท่า ๆ กันดังนั้นจึงมีการกระจายช่องสีที่ต่างกันสามช่องอย่างเท่าเทียมกัน
การกระจายของพวกเขาเป็นเช่นนี้
8 บิตสำหรับ R, 8 บิตสำหรับ G, 8 บิตสำหรับ B
เบื้องหลังภาพ 24 บิต
แตกต่างจากภาพสเกลสีเทา 8 บิตซึ่งมีหนึ่งเมทริกซ์อยู่ข้างหลังภาพ 24 บิตมีเมทริกซ์ที่แตกต่างกันสามเมทริกซ์ของ R, G, B

รูปแบบ
เป็นรูปแบบที่ใช้บ่อยที่สุด รูปแบบคือ PPM (Portable pixMap) ซึ่งรองรับโดยระบบปฏิบัติการ Linux หน้าต่างที่มีชื่อเสียงมีรูปแบบของตัวเองซึ่งก็คือ BMP (Bitmap)
ในบทช่วยสอนนี้เราจะมาดูกันว่ารหัสสีต่างๆสามารถรวมกันเพื่อสร้างสีอื่น ๆ ได้อย่างไรและเราจะซ่อนรหัสสี RGB เป็นฐานสิบหกและในทางกลับกันได้อย่างไร
รหัสสีที่แตกต่างกัน
สีทั้งหมดที่นี่เป็นรูปแบบ 24 บิตซึ่งหมายความว่าแต่ละสีจะมีสีแดง 8 บิตสีเขียว 8 บิตสีน้ำเงิน 8 บิตอยู่ในนั้น หรือเราสามารถพูดได้ว่าแต่ละสีมีสามส่วนที่แตกต่างกัน คุณต้องเปลี่ยนปริมาณของสามส่วนนี้เพื่อให้เป็นสีใดก็ได้
รูปแบบสีไบนารี
สีดำ
ภาพ:

รหัสทศนิยม:
(0,0,0)
คำอธิบาย:
ดังที่ได้อธิบายไปแล้วในบทเรียนก่อนหน้านี้ว่าในรูปแบบ 8 บิต 0 หมายถึงสีดำ ดังนั้นถ้าเราต้องทำสีดำล้วนเราต้องทำให้ R, G, B ทั้งสามส่วนเป็น 0
สี: ขาว
ภาพ:

รหัสทศนิยม:
(255,255,255)
คำอธิบาย:
เนื่องจากแต่ละส่วนของ R, G, B เป็นส่วน 8 บิต ดังนั้นใน 8 บิตสีขาวจะถูกสร้างขึ้นด้วย 255 อธิบายไว้ในบทช่วยสอนของพิกเซล ดังนั้นในการสร้างสีขาวเราตั้งค่าแต่ละส่วนเป็น 255 และนั่นคือวิธีที่เราได้สีขาว ด้วยการตั้งค่าแต่ละค่าเป็น 255 เราจะได้ค่ารวม 255 นั่นทำให้สีเป็นสีขาว
รุ่นสี RGB:
สี: แดง
ภาพ:

รหัสทศนิยม:
(255,0,0)
คำอธิบาย:
เนื่องจากเราต้องการเพียงสีแดงดังนั้นเราจึงนำส่วนที่เหลือของสองส่วนที่เหลือเป็นสีเขียวและสีน้ำเงินออกเป็นศูนย์และเราตั้งค่าส่วนสีแดงให้มากที่สุดคือ 255
สี: เขียว
ภาพ:

รหัสทศนิยม:
(0,255,0)
คำอธิบาย:
เนื่องจากเราต้องการเพียงสีเขียวดังนั้นเราจึงนำส่วนที่เหลือของสองส่วนที่เหลือเป็นสีแดงและสีน้ำเงินออกเป็นศูนย์และเราตั้งค่าส่วนสีเขียวเป็นค่าสูงสุดคือ 255
สี: น้ำเงิน
ภาพ:

รหัสทศนิยม:
(0,0,255)
คำอธิบาย:
เนื่องจากเราต้องการเพียงสีฟ้าดังนั้นเราจึงนำส่วนที่เหลือของสองส่วนที่เหลือเป็นสีแดงและสีเขียวออกเป็นศูนย์และเราตั้งค่าส่วนสีน้ำเงินไว้ที่ค่าสูงสุดคือ 255
สีเทา:
สี: เทา
ภาพ:

รหัสทศนิยม:
(128,128,128)
คำอธิบาย:
ตามที่เราได้กำหนดไว้แล้วในบทช่วยสอนเรื่องพิกเซลสีเทานั้นเป็นจุดกึ่งกลาง ในรูปแบบ 8 บิตจุดกึ่งกลางคือ 128 หรือ 127 ในกรณีนี้เราเลือก 128 ดังนั้นเราจึงตั้งค่าแต่ละส่วนเป็นจุดกึ่งกลางซึ่งเป็น 128 และส่งผลให้ค่ากลางโดยรวมและเราได้สีเทา
รุ่นสี CMYK:
CMYK เป็นรูปแบบสีอื่นที่ c ย่อมาจากสีฟ้า, m ย่อมาจาก magenta, y หมายถึงสีเหลืองและ k สำหรับสีดำ รุ่น CMYK มักใช้ในเครื่องพิมพ์สีซึ่งมีการใช้ตลับสีสองสี หนึ่งประกอบด้วย CMY และอื่น ๆ ประกอบด้วยสีดำ
สีของ CMY สามารถทำได้จากการเปลี่ยนปริมาณหรือส่วนของสีแดงสีเขียวและสีน้ำเงิน
สี: ฟ้า
ภาพ:

รหัสทศนิยม:
(0,255,255)
คำอธิบาย:
สีฟ้าเกิดจากการรวมกันของสองสีที่แตกต่างกันคือสีเขียวและสีน้ำเงิน เราจึงตั้งค่าสองค่านี้เป็นค่าสูงสุดและเราให้ส่วนของสีแดงเป็นศูนย์ และเราได้สีฟ้า
สี: Magenta
ภาพ:

รหัสทศนิยม:
(255,0,255)
คำอธิบาย:
สีม่วงแดงเกิดจากการผสมกันของสองสีที่แตกต่างกันคือสีแดงและสีน้ำเงิน เราจึงตั้งค่าสองค่านี้เป็นค่าสูงสุดและเราให้ส่วนของสีเขียวเป็นศูนย์ และเราได้สีม่วงแดง
สี: เหลือง
ภาพ:

รหัสทศนิยม:
(255,255,0)
คำอธิบาย:
สีเหลืองเกิดจากการรวมกันของสองสีที่แตกต่างกันคือสีแดงและสีเขียว เราจึงตั้งค่าสองตัวนี้เป็นค่าสูงสุดและเราให้ส่วนของสีน้ำเงินเป็นศูนย์ และเราได้สีเหลือง
การแปลง
ตอนนี้เราจะมาดูกันว่าการแปลงสีจากรูปแบบหนึ่งไปเป็นอีกรูปแบบหนึ่งอย่างไร
การแปลงจาก RGB เป็นรหัส Hex:
การแปลงจาก Hex เป็น rgb ทำได้ด้วยวิธีนี้:
ใช้สี เช่น: White = (255, 255, 255)
ใช้ส่วนแรกเช่น 255
หารด้วย 16 ดังนี้:
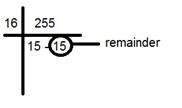
ใช้ตัวเลขสองตัวด้านล่างบรรทัดตัวประกอบและส่วนที่เหลือ ในกรณีนี้คือ 15 15 ซึ่งเป็น FF
ทำซ้ำขั้นตอนที่ 2 สำหรับสองส่วนถัดไป
รวมรหัสฐานสิบหกทั้งหมดเป็นหนึ่งเดียว
คำตอบ: #FFFFFF
การแปลงจาก Hex เป็น RGB:
การแปลงจากรหัสฐานสิบหกเป็นรูปแบบทศนิยม rgb ทำได้ด้วยวิธีนี้
ใช้เลขฐานสิบหก เช่น #FFFFFF
แบ่งตัวเลขนี้ออกเป็น 3 ส่วน: FF FF FF
ใช้ส่วนแรกและแยกส่วนประกอบ: FF
แปลงแต่ละส่วนแยกกันเป็นไบนารี: (1111) (1111)
ตอนนี้รวมไบนารีแต่ละรายการเข้าด้วยกัน: 11111111
แปลงไบนารีนี้เป็นทศนิยม: 255
ทำซ้ำขั้นตอนที่ 2 อีกสองครั้ง
ค่ามาในขั้นตอนแรกคือ R ค่าที่สองคือ G และค่าที่สามเป็นของ B
ตอบ: (255, 255, 255)
สีทั่วไปและรหัส Hex ได้รับในตารางนี้
| สี | รหัส Hex |
|---|---|
| ดำ | # 000000 |
| สีขาว | #FFFFFF |
| สีเทา | # 808080 |
| แดง | # FF0000 |
| เขียว | # 00FF00 |
| สีน้ำเงิน | # 0000FF |
| สีฟ้า | # 00FFFF |
| ม่วงแดง | # FF00FF |
| สีเหลือง | # FFFF00 |
วิธีการเฉลี่ย
วิธีถ่วงน้ำหนักหรือวิธีการส่องสว่าง
วิธีการเฉลี่ย
วิธีการเฉลี่ยเป็นวิธีที่ง่ายที่สุด คุณต้องใช้ค่าเฉลี่ยของสามสี เนื่องจากเป็นภาพ RGB ดังนั้นจึงหมายความว่าคุณได้เพิ่ม r ด้วย g ด้วย b แล้วหารด้วย 3 เพื่อให้ได้ภาพระดับสีเทาที่คุณต้องการ
มันทำด้วยวิธีนี้
ระดับสีเทา = (R + G + B) / 3
ตัวอย่างเช่น:

หากคุณมีภาพสีเหมือนภาพที่แสดงด้านบนและต้องการแปลงเป็นสีเทาโดยใช้วิธีการเฉลี่ย ผลลัพธ์ต่อไปนี้จะปรากฏขึ้น

คำอธิบาย
มีสิ่งหนึ่งที่ต้องแน่ใจคือมีบางอย่างเกิดขึ้นกับผลงานต้นฉบับ หมายความว่าวิธีการเฉลี่ยของเราใช้ได้ผล แต่ผลลัพธ์ไม่เป็นไปตามที่คาดหวัง เราต้องการแปลงภาพเป็นโทนสีเทา แต่มันกลายเป็นภาพที่ค่อนข้างดำ
ปัญหา
ปัญหานี้เกิดขึ้นเนื่องจากเราใช้ค่าเฉลี่ยของสามสี เนื่องจากสีทั้งสามสีมีความยาวคลื่นที่แตกต่างกันสามสีและมีส่วนร่วมในการสร้างภาพดังนั้นเราจึงต้องหาค่าเฉลี่ยตามการมีส่วนร่วมของพวกเขาไม่ใช่ทำโดยเฉลี่ยโดยใช้วิธีการหาค่าเฉลี่ย ตอนนี้สิ่งที่เรากำลังทำคือสิ่งนี้
33% ของสีแดง 33% ของสีเขียว 33% ของสีน้ำเงิน
เรารับ 33% ของแต่ละส่วนนั่นหมายความว่าแต่ละส่วนมีส่วนสนับสนุนในภาพเหมือนกัน แต่ในความเป็นจริงนั้นไม่ใช่อย่างนั้น วิธีการแก้ปัญหานี้ได้รับโดยวิธีการส่องสว่าง
วิธีถ่วงน้ำหนักหรือวิธีการส่องสว่าง
คุณได้เห็นปัญหาที่เกิดขึ้นในวิธีการเฉลี่ย วิธีถ่วงน้ำหนักมีวิธีแก้ปัญหานั้น เนื่องจากสีแดงมีความยาวคลื่นมากกว่าของทั้งสามสีและสีเขียวเป็นสีที่ไม่เพียง แต่มีความยาวคลื่นน้อยกว่าสีแดง แต่ยังเป็นสีเขียวที่ให้เอฟเฟกต์ผ่อนคลายแก่ดวงตามากขึ้นด้วย
หมายความว่าเราต้องลดการมีส่วนร่วมของสีแดงและเพิ่มการมีส่วนร่วมของสีเขียวและใส่สีฟ้าระหว่างสองสีนี้
ดังนั้นสมการใหม่ในรูปแบบคือ:
ภาพสีเทาใหม่ = ((0.3 * R) + (0.59 * G) + (0.11 * B))
ตามสมการนี้สีแดงมีส่วนร่วม 30% สีเขียวมีส่วนทำให้ 59% ซึ่งมากกว่าในทั้งสามสีและสีน้ำเงินมีส่วน 11%
ใช้สมการนี้กับรูปภาพเราจะได้สิ่งนี้
ภาพต้นฉบับ:

ภาพระดับสีเทา:

คำอธิบาย
ดังที่คุณเห็นที่นี่ภาพได้ถูกแปลงเป็นสีเทาอย่างถูกต้องโดยใช้วิธีการถ่วงน้ำหนัก เมื่อเปรียบเทียบกับผลลัพธ์ของวิธีการเฉลี่ยภาพนี้จะสว่างกว่า
การแปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิตอล:
เอาต์พุตของเซ็นเซอร์ภาพส่วนใหญ่เป็นสัญญาณแอนะล็อกและเราไม่สามารถใช้การประมวลผลแบบดิจิทัลกับมันได้เนื่องจากเราไม่สามารถจัดเก็บได้ เราไม่สามารถจัดเก็บได้เนื่องจากต้องใช้หน่วยความจำที่ไม่มีที่สิ้นสุดในการจัดเก็บสัญญาณที่มีค่าไม่สิ้นสุด
ดังนั้นเราจึงต้องแปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัล
ในการสร้างภาพที่เป็นดิจิทัลเราจำเป็นต้องปกปิดข้อมูลต่อเนื่องให้อยู่ในรูปแบบดิจิทัล มีสองขั้นตอนที่ทำ
Sampling
Quantization
เราจะพูดคุยเกี่ยวกับการสุ่มตัวอย่างในตอนนี้และการหาปริมาณจะถูกกล่าวถึงในภายหลัง แต่สำหรับตอนนี้เราจะพูดถึงความแตกต่างระหว่างสองสิ่งนี้และความต้องการของสองขั้นตอนนี้
แนวคิดพื้นฐาน:
แนวคิดพื้นฐานเบื้องหลังการแปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัลคือ

เพื่อแปลงแกนทั้งสอง (x, y) เป็นรูปแบบดิจิทัล
เนื่องจากภาพไม่ต่อเนื่องไม่เพียง แต่ในพิกัด (แกน x) แต่ยังอยู่ในแอมพลิจูด (แกน y) ด้วยดังนั้นส่วนที่เกี่ยวข้องกับการกำหนดพิกัดเป็นดิจิทัลจึงเรียกว่าการสุ่มตัวอย่าง และส่วนที่เกี่ยวข้องกับการทำให้แอมพลิจูดเป็นดิจิทัลนั้นเรียกว่า quantization
การสุ่มตัวอย่าง
การสุ่มตัวอย่างได้รับการแนะนำในบทแนะนำเบื้องต้นเกี่ยวกับสัญญาณและระบบแล้ว แต่เราจะพูดถึงที่นี่เพิ่มเติม
นี่คือสิ่งที่เราได้พูดคุยเกี่ยวกับการสุ่มตัวอย่าง
คำว่าการสุ่มตัวอย่างหมายถึงการเก็บตัวอย่าง
เราแปลงแกน x เป็นดิจิทัลในการสุ่มตัวอย่าง
มันทำกับตัวแปรอิสระ
ในกรณีของสมการ y = sin (x) จะทำกับตัวแปร x
แบ่งออกเป็นสองส่วนเพิ่มเติมคือการสุ่มตัวอย่างและการสุ่มตัวอย่างลง

หากคุณดูรูปด้านบนคุณจะเห็นว่ามีรูปแบบสุ่มบางอย่างในสัญญาณ รูปแบบเหล่านี้เกิดจากเสียงรบกวน ในการสุ่มตัวอย่างเราลดเสียงดังกล่าวโดยการเก็บตัวอย่าง เห็นได้ชัดว่าเราใช้ตัวอย่างมากขึ้นคุณภาพของภาพจะดีขึ้นสัญญาณรบกวนจะถูกลบออกมากขึ้นและในทางกลับกันก็เกิดขึ้นเช่นเดียวกัน
อย่างไรก็ตามหากคุณทำการสุ่มตัวอย่างบนแกน x สัญญาณจะไม่ถูกแปลงเป็นรูปแบบดิจิทัลเว้นแต่คุณจะทำการสุ่มตัวอย่างแกน y ด้วยซึ่งเรียกว่า quantization ยิ่งในที่สุดตัวอย่างก็หมายความว่าคุณกำลังรวบรวมข้อมูลมากขึ้นและในกรณีของภาพก็หมายถึงพิกเซลที่มากขึ้น
ความสัมพันธ์มาพร้อมกับพิกเซล
เนื่องจากพิกเซลเป็นองค์ประกอบที่เล็กที่สุดในรูปภาพ จำนวนพิกเซลทั้งหมดในภาพสามารถคำนวณได้เป็น
Pixels = จำนวนแถวทั้งหมด * จำนวนคอลัมน์ทั้งหมด
สมมติว่าเรามีพิกเซลทั้งหมด 25 พิกเซลนั่นหมายความว่าเรามีภาพสี่เหลี่ยมจัตุรัสขนาด 5 X 5 จากนั้นเมื่อเราได้ทำการสุ่มตัวอย่างด้านบนแล้วตัวอย่างที่มากขึ้นจะทำให้ได้พิกเซลมากขึ้นในที่สุด นั่นหมายความว่าสัญญาณต่อเนื่องของเราเราได้ตัวอย่าง 25 ตัวอย่างบนแกน x นั่นหมายถึง 25 พิกเซลของภาพนี้
สิ่งนี้นำไปสู่ข้อสรุปอีกประการหนึ่งว่าเนื่องจากพิกเซลเป็นส่วนที่เล็กที่สุดของอาร์เรย์ CCD ดังนั้นมันหมายความว่ามันมีความสัมพันธ์กับอาร์เรย์ CCD ด้วยซึ่งสามารถอธิบายได้ดังนี้
ความสัมพันธ์กับอาร์เรย์ CCD
จำนวนเซ็นเซอร์บนอาร์เรย์ CCD จะเท่ากับจำนวนพิกเซลโดยตรง และเนื่องจากเราได้ข้อสรุปว่าจำนวนพิกเซลเท่ากับจำนวนตัวอย่างโดยตรงนั่นหมายความว่าตัวอย่างจำนวนนั้นเท่ากับจำนวนเซ็นเซอร์บนอาร์เรย์ CCD โดยตรง
การสุ่มตัวอย่างมากเกินไป
ในตอนแรกเราได้กำหนดว่าการสุ่มตัวอย่างแบ่งออกเป็นสองประเภทเพิ่มเติม ซึ่งขึ้นอยู่กับการสุ่มตัวอย่างและการสุ่มตัวอย่างลง การสุ่มตัวอย่างขึ้นเรียกอีกอย่างว่าการสุ่มตัวอย่างเกิน
การสุ่มตัวอย่างเกินขนาดมีแอปพลิเคชั่นที่ลึกมากในการประมวลผลภาพซึ่งเรียกว่าการซูม
การซูม
เราจะแนะนำการซูมอย่างเป็นทางการในบทช่วยสอนที่กำลังจะมาถึง แต่สำหรับตอนนี้เราจะอธิบายสั้น ๆ เกี่ยวกับการซูม
การซูมหมายถึงการเพิ่มจำนวนพิกเซลดังนั้นเมื่อคุณซูมภาพคุณจะเห็นรายละเอียดมากขึ้น
การเพิ่มจำนวนพิกเซลทำได้โดยการสุ่มตัวอย่างมากเกินไป วิธีหนึ่งในการซูมคือหรือเพื่อเพิ่มจำนวนตัวอย่างคือการซูมแบบออปติกผ่านการเคลื่อนไหวของมอเตอร์ของเลนส์แล้วจึงจับภาพ แต่เราต้องทำเมื่อจับภาพได้แล้ว
มีความแตกต่างระหว่างการซูมและการสุ่มตัวอย่าง
แนวคิดเหมือนกันคือเพิ่มกลุ่มตัวอย่าง แต่ความแตกต่างที่สำคัญคือในขณะที่ทำการสุ่มตัวอย่างสัญญาณการซูมจะกระทำบนภาพดิจิทัล
ก่อนที่เราจะกำหนดความละเอียดพิกเซลจำเป็นต้องกำหนดพิกเซล
พิกเซล
เราได้กำหนดพิกเซลไว้แล้วในบทแนะนำเกี่ยวกับแนวคิดของพิกเซลซึ่งเรากำหนดพิกเซลเป็นองค์ประกอบที่เล็กที่สุดของภาพ นอกจากนี้เรายังกำหนดให้พิกเซลสามารถจัดเก็บค่าตามสัดส่วนของความเข้มของแสง ณ ตำแหน่งนั้น ๆ
ตอนนี้เนื่องจากเราได้กำหนดพิกเซลแล้วเราจะกำหนดว่าอะไรคือความละเอียด
ความละเอียด
ความละเอียดสามารถกำหนดได้หลายวิธี เช่นความละเอียดพิกเซล, ความละเอียดเชิงพื้นที่, ความละเอียดชั่วคราว, ความละเอียดสเปกตรัม ซึ่งเราจะพูดถึงความละเอียดพิกเซล
คุณอาจเคยเห็นว่าในการตั้งค่าคอมพิวเตอร์ของคุณเองคุณมีความละเอียดจอภาพ 800 x 600, 640 x 480 เป็นต้น
ในความละเอียดพิกเซลคำว่าความละเอียดหมายถึงจำนวนพิกเซลทั้งหมดในภาพดิจิทัล ตัวอย่างเช่น. หากรูปภาพมีแถว M และ N คอลัมน์ความละเอียดสามารถกำหนดเป็น MX N ได้
หากเรากำหนดความละเอียดเป็นจำนวนพิกเซลทั้งหมดความละเอียดของพิกเซลสามารถกำหนดได้ด้วยชุดตัวเลขสองตัว ตัวเลขแรกคือความกว้างของรูปภาพหรือพิกเซลข้ามคอลัมน์และตัวเลขที่สองคือความสูงของรูปภาพหรือพิกเซลที่มีความกว้าง
เราสามารถพูดได้ว่ายิ่งความละเอียดของพิกเซลสูงเท่าใดคุณภาพของภาพก็ยิ่งสูงขึ้นเท่านั้น
เราสามารถกำหนดความละเอียดพิกเซลของภาพเป็น 4500 X 5500
ล้านพิกเซล
เราสามารถคำนวณเมกะพิกเซลของกล้องโดยใช้ความละเอียดพิกเซล
พิกเซลคอลัมน์ (กว้าง) X แถวพิกเซล (สูง) / 1 ล้าน
ขนาดของภาพสามารถกำหนดได้ด้วยความละเอียดพิกเซล
ขนาด = ความละเอียดพิกเซล X bpp (บิตต่อพิกเซล)
การคำนวณเมกะพิกเซลของกล้อง
สมมติว่าเรามีภาพขนาด 2500 X 3192
ความละเอียดพิกเซล = 2500 * 3192 = 7982350 ไบต์
หารด้วย 1 ล้าน = 7.9 = 8 เมกะพิกเซล (โดยประมาณ)
อัตราส่วนภาพ
อีกแนวคิดที่สำคัญเกี่ยวกับความละเอียดของพิกเซลคืออัตราส่วนภาพ
อัตราส่วนภาพคืออัตราส่วนระหว่างความกว้างของรูปภาพและความสูงของรูปภาพ โดยทั่วไปมักอธิบายว่าเป็นตัวเลขสองตัวคั่นด้วยเครื่องหมายจุดคู่ (8: 9) อัตราส่วนนี้แตกต่างกันในภาพที่แตกต่างกันและในหน้าจอที่แตกต่างกัน อัตราส่วนภาพทั่วไปคือ:
1.33: 1, 1.37: 1, 1.43: 1, 1.50: 1, 1.56: 1, 1.66: 1, 1.75: 1, 1.78: 1, 1.85: 1, 2.00: 1 ฯลฯ
ความได้เปรียบ:
อัตราส่วนภาพจะรักษาความสมดุลระหว่างลักษณะที่ปรากฏของภาพบนหน้าจอหมายความว่าจะรักษาอัตราส่วนระหว่างพิกเซลแนวนอนและแนวตั้ง ไม่ให้ภาพบิดเบี้ยวเมื่ออัตราส่วนกว้างยาวเพิ่มขึ้น
ตัวอย่างเช่น:
นี่คือภาพตัวอย่างซึ่งมี 100 แถวและ 100 คอลัมน์ หากเราต้องการให้มีขนาดเล็กลงและเงื่อนไขก็คือคุณภาพยังคงเหมือนเดิมหรือในลักษณะอื่น ๆ ที่ภาพไม่ผิดเพี้ยนนี่จะเกิดขึ้นได้อย่างไร
ภาพต้นฉบับ:

การเปลี่ยนแถวและคอลัมน์โดยรักษาอัตราส่วนใน MS Paint
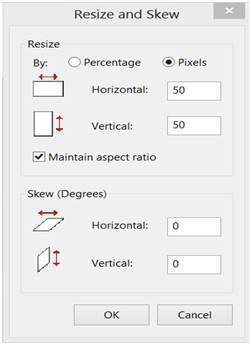
ผลลัพธ์

ภาพเล็กลง แต่มีความสมดุลเท่ากัน
คุณอาจเคยเห็นอัตราส่วนภาพในโปรแกรมเล่นวิดีโอซึ่งคุณสามารถปรับวิดีโอตามความละเอียดหน้าจอของคุณได้
การค้นหาขนาดของภาพจากอัตราส่วนภาพ:
อัตราส่วนภาพบอกเราได้หลายอย่าง ด้วยอัตราส่วนภาพคุณสามารถคำนวณขนาดของภาพพร้อมกับขนาดของภาพได้
ตัวอย่างเช่น
หากคุณได้รับรูปภาพที่มีอัตราส่วน 6: 2 ของรูปภาพที่มีความละเอียดพิกเซล 480000 พิกเซลเนื่องจากรูปภาพนั้นเป็นภาพสเกลสีเทา
และคุณจะถูกขอให้คำนวณสองสิ่ง
แก้ไขความละเอียดของพิกเซลเพื่อคำนวณขนาดของภาพ
คำนวณขนาดของภาพ
วิธีการแก้:
ให้:
อัตราส่วนภาพ: c: r = 6: 2
ความละเอียดพิกเซล: c * r = 480000
บิตต่อพิกเซล: ภาพระดับสีเทา = 8bpp
หา:
จำนวนแถว =?
จำนวน cols =?
การแก้ส่วนแรก:
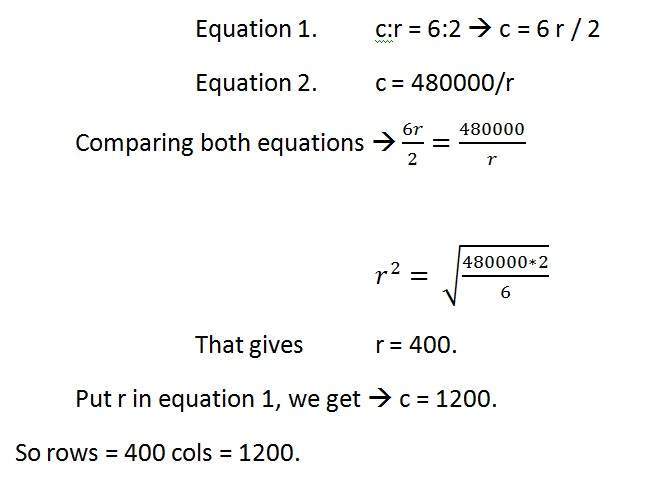
การแก้ส่วนที่ 2:
ขนาด = แถว * cols * bpp
ขนาดของภาพเป็นบิต = 400 * 1200 * 8 = 3840000 บิต
ขนาดของภาพเป็นไบต์ = 480000 ไบต์
ขนาดของภาพเป็นกิโลไบต์ = 48 กิโลไบต์ (โดยประมาณ)
ในบทช่วยสอนนี้เราจะแนะนำแนวคิดเกี่ยวกับการซูมและเทคนิคทั่วไปที่ใช้ในการซูมภาพ
การซูม
การซูมหมายถึงการขยายภาพโดยให้รายละเอียดในภาพสามารถมองเห็นได้ชัดเจนขึ้น การซูมภาพมีแอพพลิเคชั่นมากมายตั้งแต่การซูมผ่านเลนส์กล้องไปจนถึงการซูมภาพบนอินเทอร์เน็ตเป็นต้น
ตัวอย่างเช่น

ถูกซูมเข้า

คุณสามารถซูมบางอย่างได้สองขั้นตอน
ขั้นตอนแรกรวมถึงการซูมก่อนที่จะถ่ายภาพใดภาพหนึ่ง สิ่งนี้เรียกว่าการซูมก่อนการประมวลผล การซูมนี้เกี่ยวข้องกับฮาร์ดแวร์และการเคลื่อนไหวของกลไก
ขั้นตอนที่สองคือการซูมเมื่อจับภาพได้แล้ว มันทำผ่านอัลกอริทึมต่างๆมากมายที่เราปรับแต่งพิกเซลเพื่อซูมเข้าไปในส่วนที่ต้องการ
เราจะพูดถึงรายละเอียดในบทช่วยสอนถัดไป
ซูมออปติคอลเทียบกับซูมดิจิตอล
กล้องรองรับการซูมสองประเภทนี้
ซูมออปติคอล:
การซูมแบบออปติคอลทำได้โดยใช้การเคลื่อนไหวของเลนส์กล้องของคุณ การซูมแบบออปติคอลคือการซูมที่แท้จริง ผลลัพธ์ของการซูมออปติคอลนั้นดีกว่าการซูมแบบดิจิตอลมาก ในการซูมแบบออปติคอลภาพจะถูกขยายโดยเลนส์ในลักษณะที่วัตถุในภาพดูเหมือนจะอยู่ใกล้กับกล้องมากขึ้น ในการซูมออปติคอลเลนส์จะขยายทางกายภาพเพื่อซูมหรือขยายวัตถุ
ซูมแบบดิจิตอล:
การซูมดิจิตอลโดยทั่วไปเป็นการประมวลผลภาพภายในกล้อง ในระหว่างการซูมดิจิตอลศูนย์กลางของภาพจะขยายและขอบของภาพจะถูกครอบตัดออก เนื่องจากศูนย์กลางขยายดูเหมือนว่าวัตถุจะอยู่ใกล้คุณมากขึ้น
ในระหว่างการซูมแบบดิจิทัลพิกเซลจะขยายออกเนื่องจากคุณภาพของภาพลดลง
ผลเช่นเดียวกันของการซูมดิจิตอลสามารถเห็นได้หลังจากถ่ายภาพผ่านคอมพิวเตอร์ของคุณโดยใช้กล่องเครื่องมือ / ซอฟต์แวร์ประมวลผลภาพเช่น Photoshop
ภาพต่อไปนี้เป็นผลมาจากการซูมแบบดิจิตอลโดยใช้วิธีใดวิธีหนึ่งต่อไปนี้ที่ระบุไว้ด้านล่างในวิธีการซูม

ตอนนี้เนื่องจากเรากำลังใช้การประมวลผลภาพดิจิทัลเราจึงไม่โฟกัสว่าจะซูมภาพได้อย่างไรโดยใช้เลนส์หรือสิ่งอื่น ๆ แต่เราจะมุ่งเน้นไปที่วิธีการซึ่งช่วยให้สามารถซูมภาพดิจิทัลได้
วิธีการซูม:
แม้ว่าจะมีหลายวิธีที่ใช้ได้ผล แต่เราจะพูดถึงวิธีการที่พบบ่อยที่สุดที่นี่
ตามรายการด้านล่าง
การจำลองพิกเซลหรือ (การแก้ไขเพื่อนบ้านที่ใกล้ที่สุด)
วิธีการระงับคำสั่งซื้อเป็นศูนย์
ซูม K ครั้ง
ทั้งสามวิธีนี้แนะนำอย่างเป็นทางการในบทช่วยสอนถัดไป
ในบทช่วยสอนนี้เราจะแนะนำวิธีการซูมสามวิธีอย่างเป็นทางการที่แนะนำในบทแนะนำเกี่ยวกับการซูมเบื้องต้น
วิธีการ
การจำลองพิกเซลหรือ (การแก้ไขเพื่อนบ้านที่ใกล้ที่สุด)
วิธีการระงับคำสั่งซื้อเป็นศูนย์
ซูม K ครั้ง
แต่ละวิธีมีข้อดีและข้อเสียของตัวเอง เราจะเริ่มต้นด้วยการพูดคุยเกี่ยวกับการจำลองแบบพิกเซล
วิธีที่ 1: การจำลองแบบพิกเซล:
บทนำ:
เรียกอีกอย่างว่าการแก้ไขเพื่อนบ้านที่ใกล้ที่สุด ตามชื่อของมันในวิธีนี้เราเพียงแค่จำลองพิกเซลข้างเคียง ดังที่เราได้กล่าวไปแล้วในบทช่วยสอนเรื่องการสุ่มตัวอย่างการซูมนั้นไม่ได้เป็นเพียงการเพิ่มจำนวนของตัวอย่างหรือพิกเซล อัลกอริทึมนี้ทำงานบนหลักการเดียวกัน
การทำงาน:
ในวิธีนี้เราสร้างพิกเซลใหม่จากพิกเซลที่กำหนดไว้แล้ว แต่ละพิกเซลจะจำลองแบบด้วยวิธีนี้ n เท่าของแถวที่ชาญฉลาดและคอลัมน์ที่ชาญฉลาดและคุณจะได้ภาพที่ซูม ง่ายๆแค่นั้นเอง
ตัวอย่างเช่น:
หากคุณมีรูปภาพ 2 แถวและ 2 คอลัมน์และคุณต้องการซูมสองครั้งหรือ 2 ครั้งโดยใช้การจำลองพิกเซลคุณสามารถทำได้ที่นี่
เพื่อความเข้าใจที่ดีขึ้นภาพจึงถูกถ่ายในรูปแบบของเมทริกซ์โดยมีค่าพิกเซลของภาพ
| 1 | 2 |
| 3 | 4 |
ภาพด้านบนมีสองแถวและสองคอลัมน์ก่อนอื่นเราจะซูมเข้าแถวอย่างชาญฉลาด
การซูมแถวที่ชาญฉลาด:
เมื่อเราซูมเข้าแถวอย่างชาญฉลาดเราก็แค่คัดลอกพิกเซลของแถวไปยังเซลล์ใหม่ที่อยู่ติดกัน
นี่คือวิธีการทำ
| 1 | 1 | 2 | 2 |
| 3 | 3 | 4 | 4 |
ดังที่คุณสามารถทำได้ในเมทริกซ์ด้านบนแต่ละพิกเซลจะถูกจำลองซ้ำสองครั้งในแถว
การซูมขนาดคอลัมน์:
ขั้นตอนต่อไปคือการจำลองคอลัมน์พิกเซลแต่ละคอลัมน์อย่างชาญฉลาดซึ่งเราจะคัดลอกพิกเซลของคอลัมน์ไปยังคอลัมน์ใหม่ที่อยู่ติดกันหรืออยู่ด้านล่าง
นี่คือวิธีการทำ
| 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 2 |
| 3 | 3 | 4 | 4 |
| 3 | 3 | 4 | 4 |
ขนาดภาพใหม่:
ดังที่เห็นได้จากตัวอย่างด้านบนภาพต้นฉบับ 2 แถวและ 2 คอลัมน์ถูกแปลงเป็น 4 แถวและ 4 คอลัมน์หลังจากการซูม นั่นหมายถึงภาพใหม่มีขนาด
(แถวภาพต้นฉบับ * ปัจจัยการซูม, ภาพต้นฉบับ * ปัจจัยการซูม)
ข้อดีและข้อเสีย:
ข้อดีอย่างหนึ่งของเทคนิคการซูมนี้คือมันง่ายมาก คุณต้องคัดลอกพิกเซลและไม่มีอะไรอื่น
ข้อเสียของเทคนิคนี้คือภาพถูกซูม แต่เอาต์พุตเบลอมาก และเมื่อปัจจัยการซูมเพิ่มขึ้นภาพก็เบลอมากขึ้นเรื่อย ๆ ซึ่งจะส่งผลให้ภาพเบลออย่างสมบูรณ์ในที่สุด
วิธีที่ 2: การระงับคำสั่งซื้อเป็นศูนย์
บทนำ
วิธีการระงับคำสั่งศูนย์เป็นอีกวิธีหนึ่งในการซูม เรียกอีกอย่างว่าซูมสองครั้ง เพราะซูมได้แค่สองครั้ง. เราจะเห็นในตัวอย่างด้านล่างว่าเหตุใดจึงทำเช่นนั้น
กำลังทำงาน
ในวิธีการระงับลำดับศูนย์เราเลือกองค์ประกอบที่อยู่ติดกันสองรายการจากแถวตามลำดับจากนั้นเราจึงเพิ่มและหารผลลัพธ์ด้วยสองและวางผลลัพธ์ไว้ระหว่างสององค์ประกอบนั้น ก่อนอื่นเราทำแถวนี้อย่างชาญฉลาดจากนั้นเราทำคอลัมน์นี้อย่างชาญฉลาด
ตัวอย่างเช่น
ให้ถ่ายภาพขนาด 2 แถวและ 2 คอลัมน์แล้วซูมสองครั้งโดยใช้การระงับลำดับศูนย์
| 1 | 2 |
| 3 | 4 |
ก่อนอื่นเราจะขยายแถวอย่างชาญฉลาดจากนั้นคอลัมน์ที่ชาญฉลาด
การซูมแถวอย่างชาญฉลาด
| 1 | 1 | 2 |
| 3 | 3 | 4 |
เมื่อเราหาตัวเลขสองตัวแรก: (2 + 1) = 3 แล้วเราหารด้วย 2 เราจะได้ 1.5 ซึ่งประมาณเป็น 1 วิธีเดียวกันนี้จะถูกนำไปใช้ในแถวที่ 2
การซูมคอลัมน์อย่างชาญฉลาด
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 3 | 4 |
เราเอาค่าพิกเซลของคอลัมน์ที่อยู่ติดกัน 2 ค่าซึ่งก็คือ 1 และ 3 เราบวกมันเข้าไปและได้ 4. 4 หารด้วย 2 และเราจะได้ 2 ซึ่งอยู่ระหว่างค่าเหล่านั้น ใช้วิธีการเดียวกันในทุกคอลัมน์
ขนาดภาพใหม่
ดังที่คุณเห็นว่าขนาดของรูปภาพใหม่คือ 3 x 3 โดยที่ขนาดของรูปภาพต้นฉบับคือ 2 x 2 ดังนั้นจึงหมายความว่าขนาดของรูปภาพใหม่จะขึ้นอยู่กับสูตรต่อไปนี้
(2 (จำนวนแถว) ลบ 1) X (2 (จำนวนคอลัมน์) ลบ 1)
ข้อดีและข้อเสีย
ข้อดีอย่างหนึ่งของเทคนิคการซูมนี้คือไม่ได้สร้างภาพเบลอเมื่อเทียบกับวิธีการแก้ไขเพื่อนบ้านที่ใกล้ที่สุด แต่มันก็มีข้อเสียตรงที่มันสามารถทำงานได้ด้วยพลังของ 2 เท่านั้นสามารถแสดงได้ที่นี่
เหตุผลเบื้องหลังการซูมสองครั้ง:
พิจารณารูปภาพ 2 แถวด้านบนและ 2 คอลัมน์ ถ้าเราต้องซูม 6 เท่าโดยใช้วิธี zero order hold ก็ไม่สามารถทำได้ ตามสูตรที่แสดงให้เราเห็นนี้
มันสามารถซูมได้เพียง 2 2,4,8,16,32 และอื่น ๆ
แม้ว่าคุณจะพยายามซูมก็ไม่สามารถทำได้ เนื่องจากในตอนแรกเมื่อคุณจะซูมสองครั้งและผลลัพธ์จะเหมือนกับที่แสดงในคอลัมน์การซูมที่ชาญฉลาดด้วยขนาดเท่ากับ 3x3 จากนั้นคุณจะซูมอีกครั้งและคุณจะได้ขนาดเท่ากับ 5 x 5 ตอนนี้ถ้าคุณจะทำอีกครั้งคุณจะได้ขนาดเท่ากับ 9 x 9
ในขณะที่ตามสูตรของคุณคำตอบควรเป็น 11x11 เป็น (6 (2) ลบ 1) X (6 (2) ลบ 1) ให้ 11 x 11
วิธีที่ 3: การซูม K-Times
บทนำ:
K times เป็นวิธีการซูมที่สามที่เราจะพูดถึง เป็นหนึ่งในอัลกอริทึมการซูมที่สมบูรณ์แบบที่สุดที่กล่าวถึง รองรับความท้าทายทั้งการซูมสองครั้งและการจำลองพิกเซล K ในอัลกอริทึมการซูมนี้หมายถึงปัจจัยการซูม
การทำงาน:
มันทำงานในลักษณะนี้
ก่อนอื่นคุณต้องใช้สองพิกเซลที่อยู่ติดกันเหมือนที่คุณทำในการซูมสองครั้ง จากนั้นคุณต้องลบสิ่งที่เล็กกว่าออกจากค่าที่มากกว่า เราเรียกผลลัพธ์นี้ว่า (OP)
แบ่งเอาต์พุต (OP) ด้วยปัจจัยการซูม (K) ตอนนี้คุณต้องเพิ่มผลลัพธ์ให้เป็นค่าที่น้อยลงและใส่ผลลัพธ์ไว้ระหว่างสองค่านั้น
เพิ่มค่า OP อีกครั้งให้กับค่าที่คุณเพิ่งใส่และวางอีกครั้งถัดจากค่าที่ใส่ก่อนหน้านี้ คุณต้องทำจนกว่าคุณจะวางค่า k-1 ลงไป
ทำซ้ำขั้นตอนเดียวกันสำหรับแถวและคอลัมน์ทั้งหมดและคุณจะได้ภาพที่ซูม
ตัวอย่างเช่น:
สมมติว่าคุณมีรูปภาพ 2 แถวและ 3 คอลัมน์ซึ่งได้รับด้านล่าง และคุณต้องซูมสามครั้งหรือสามครั้ง
| 15 | 30 | 15 |
| 30 | 15 | 30 |
K ในกรณีนี้คือ 3 K = 3
จำนวนค่าที่ควรแทรกคือ k-1 = 3-1 = 2
การซูมแถวอย่างชาญฉลาด
ใช้สองพิกเซลแรกที่อยู่ติดกัน ซึ่ง ได้แก่ 15 และ 30
ลบ 15 จาก 30 30-15 = 15
หาร 15 ด้วย k. 15 / k = 15/3 = 5 เราเรียกมันว่า OP (โดยที่ op เป็นเพียงชื่อ)
เพิ่ม OP ลงในตัวเลขที่ต่ำกว่า 15 + OP = 15 + 5 = 20
เพิ่ม OP เป็น 20 อีกครั้ง 20 + OP = 20 + 5 = 25
เราทำ 2 ครั้งเพราะเราต้องใส่ค่า k-1
ทำซ้ำขั้นตอนนี้สำหรับสองพิกเซลที่อยู่ติดกันถัดไป แสดงไว้ในตารางแรก
หลังจากแทรกค่าแล้วคุณต้องเรียงค่าที่แทรกตามลำดับจากน้อยไปมากดังนั้นจึงยังคงมีความสมมาตรระหว่างค่าเหล่านี้
จะแสดงในตารางที่สอง
ตารางที่ 1.
| 15 | 20 | 25 | 30 | 20 | 25 | 15 |
| 30 | 20 | 25 | 15 | 20 | 25 | 30 |
ตารางที่ 2.

การซูมคอลัมน์อย่างชาญฉลาด
ขั้นตอนเดียวกันจะต้องดำเนินการคอลัมน์อย่างชาญฉลาด ขั้นตอนนี้รวมถึงการรับค่าพิกเซลสองค่าที่อยู่ติดกันแล้วลบค่าที่เล็กกว่าออกจากค่าที่ใหญ่กว่า หลังจากนั้นคุณต้องหารด้วย k จัดเก็บผลลัพธ์เป็น OP เพิ่ม OP ให้เล็กลงจากนั้นเพิ่ม OP อีกครั้งในค่าที่มาจากการเพิ่มครั้งแรกของ OP แทรกค่าใหม่
นี่คือสิ่งที่คุณได้รับหลังจากนั้น
| 15 | 20 | 25 | 30 | 25 | 20 | 15 |
| 20 | 21 | 21 | 25 | 21 | 21 | 20 |
| 25 | 22 | 22 | 20 | 22 | 22 | 25 |
| 30 | 25 | 20 | 15 | 20 | 25 | 30 |
ขนาดภาพใหม่
วิธีที่ดีที่สุดในการคำนวณสูตรสำหรับขนาดของรูปภาพใหม่คือการเปรียบเทียบขนาดของรูปภาพต้นฉบับกับรูปภาพสุดท้าย ขนาดของรูปภาพต้นฉบับคือ 2 X 3 และขนาดของรูปภาพใหม่คือ 4 x 7
สูตรจึงเป็น:
(K (จำนวนแถวลบ 1) + 1) X (K (จำนวน cols ลบ 1) + 1)
ข้อดีและข้อเสีย
ข้อได้เปรียบที่ชัดเจนอย่างหนึ่งของอัลกอริทึมการซูมเวลา k คือสามารถคำนวณการซูมของปัจจัยใด ๆ ที่เป็นพลังของอัลกอริธึมการจำลองแบบพิกเซลและยังให้ผลลัพธ์ที่ดีขึ้น (เบลอน้อยลง) ซึ่งเป็นพลังของวิธีการระงับคำสั่งเป็นศูนย์ ดังนั้นจึงประกอบด้วยพลังของสองอัลกอริทึม
ความยากเพียงอย่างเดียวของอัลกอริทึมนี้คือต้องเรียงลำดับในตอนท้ายซึ่งเป็นขั้นตอนเพิ่มเติมและทำให้ต้นทุนในการคำนวณเพิ่มขึ้น
ความละเอียดของภาพ
ความละเอียดของภาพสามารถกำหนดได้หลายวิธี ประเภทหนึ่งซึ่งเป็นความละเอียดพิกเซลที่ได้รับการกล่าวถึงในบทช่วยสอนเกี่ยวกับความละเอียดพิกเซลและอัตราส่วนภาพ
ในบทช่วยสอนนี้เราจะกำหนดความละเอียดอีกประเภทหนึ่งซึ่งก็คือความละเอียดเชิงพื้นที่
ความละเอียดเชิงพื้นที่:
ความละเอียดเชิงพื้นที่ระบุว่าความคมชัดของภาพไม่สามารถกำหนดได้ด้วยความละเอียดของพิกเซล จำนวนพิกเซลในภาพไม่สำคัญ
ความละเอียดเชิงพื้นที่สามารถกำหนดเป็นไฟล์
รายละเอียดที่เล็กที่สุดในภาพที่มองเห็นได้ (การประมวลผลภาพดิจิทัล - Gonzalez, Woods - 2nd Edition)
หรือในทางอื่นเราสามารถกำหนดความละเอียดเชิงพื้นที่เป็นจำนวนพิกเซลอิสระต่อนิ้ว
ในระยะสั้นความละเอียดเชิงพื้นที่หมายถึงเราไม่สามารถเปรียบเทียบภาพสองประเภทที่แตกต่างกันเพื่อดูว่าภาพใดชัดเจนหรือภาพใดไม่ชัดเจน หากเราต้องเปรียบเทียบทั้งสองภาพเพื่อดูว่าภาพใดชัดเจนกว่าหรือมีความละเอียดเชิงพื้นที่มากกว่าเราจะต้องเปรียบเทียบภาพสองภาพที่มีขนาดเท่ากัน
ตัวอย่างเช่น:
คุณไม่สามารถเปรียบเทียบสองภาพนี้เพื่อดูความชัดเจนของภาพได้


แม้ว่าทั้งสองภาพจะเป็นภาพคนเดียวกัน แต่นั่นไม่ใช่เงื่อนไขที่เรากำลังตัดสิน ภาพทางด้านซ้ายคือภาพของ Einstein ที่มีขนาด 227 x 222 ออกมาในขณะที่ภาพทางด้านขวามีขนาด 980 X 749 และยังเป็นภาพที่มีการซูม เราไม่สามารถเปรียบเทียบให้เห็นว่าอันไหนชัดเจนกว่ากัน โปรดจำไว้ว่าปัจจัยของการซูมไม่สำคัญในเงื่อนไขนี้สิ่งเดียวที่สำคัญคือสองภาพนี้ไม่เท่ากัน
ดังนั้นในการวัดความละเอียดเชิงพื้นที่รูปภาพด้านล่างจะแสดงวัตถุประสงค์


ตอนนี้คุณสามารถเปรียบเทียบสองภาพนี้ ทั้งสองภาพมีขนาดเท่ากันซึ่งมีขนาด 227 X 222 เมื่อเปรียบเทียบกันแล้วคุณจะเห็นว่าภาพทางด้านซ้ายมีความละเอียดเชิงพื้นที่มากกว่าหรือมีความชัดเจนมากกว่าภาพทางด้านขวา นั่นเป็นเพราะภาพทางขวามือเป็นภาพเบลอ
การวัดความละเอียดเชิงพื้นที่:
เนื่องจากความละเอียดเชิงพื้นที่หมายถึงความชัดเจนดังนั้นสำหรับอุปกรณ์ที่แตกต่างกันจึงมีการวัดที่แตกต่างกันเพื่อวัด
ตัวอย่างเช่น:
จุดต่อนิ้ว
เส้นต่อนิ้ว
พิกเซลต่อนิ้ว
พวกเขาจะกล่าวถึงรายละเอียดเพิ่มเติมในบทช่วยสอนถัดไป แต่มีการแนะนำสั้น ๆ ไว้ด้านล่าง
จุดต่อนิ้ว:
จุดต่อนิ้วหรือ DPI มักใช้ในจอภาพ
เส้นต่อนิ้ว:
เส้นต่อนิ้วหรือ LPI มักใช้ในเครื่องพิมพ์เลเซอร์
พิกเซลต่อนิ้ว:
พิกเซลต่อนิ้วหรือ PPI วัดได้สำหรับอุปกรณ์ต่างๆเช่นแท็บเล็ตโทรศัพท์มือถือเป็นต้น
ในบทแนะนำเกี่ยวกับการแก้ปัญหาเชิงพื้นที่ก่อนหน้านี้เราได้พูดถึงการแนะนำสั้น ๆ ของ PPI, DPI, LPI ตอนนี้เรากำลังจะหารืออย่างเป็นทางการทั้งหมด
พิกเซลต่อนิ้ว
ความหนาแน่นของพิกเซลหรือพิกเซลต่อนิ้วเป็นการวัดความละเอียดเชิงพื้นที่สำหรับอุปกรณ์ต่างๆซึ่งรวมถึงแท็บเล็ตโทรศัพท์มือถือ
ยิ่ง PPI สูงเท่าไหร่คุณภาพก็ยิ่งสูงขึ้นเท่านั้น เพื่อให้เข้าใจมากขึ้นว่ามันคำนวณอย่างไร ให้คำนวณ PPI ของโทรศัพท์มือถือ
การคำนวณพิกเซลต่อนิ้ว (PPI) ของ Samsung galaxy S4:

Samsung galaxy s4 มี PPI หรือความหนาแน่นของพิกเซล 441 แต่จะคำนวณอย่างไร?
ก่อนอื่นเราจะใช้ทฤษฎีบท Pythagoras เพื่อคำนวณความละเอียดของเส้นทแยงมุมเป็นพิกเซล
สามารถกำหนดเป็น:
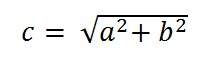
โดยที่ a และ b คือความละเอียดความสูงและความกว้างในพิกเซลและ c คือความละเอียดแนวทแยงเป็นพิกเซล
สำหรับ Samsung galaxy s4 มีขนาด 1080 x 1920 พิกเซล
ดังนั้นการใส่ค่าเหล่านั้นลงในสมการจะได้ผลลัพธ์
C = 2202.90717
ตอนนี้เราจะคำนวณ PPI
PPI = c / ขนาดเส้นทแยงมุมเป็นนิ้ว
ขนาดเส้นทแยงมุมเป็นนิ้วของ Samsun galaxy s4 คือ 5.0 นิ้วซึ่งสามารถยืนยันได้จากทุกที่
PPI = 2202.90717 / 5.0
PPI = 440.58
PPI = 441 (โดยประมาณ)
นั่นหมายความว่าความหนาแน่นของพิกเซลของ Samsung galaxy s4 คือ 441 PPI
จุดต่อนิ้ว.
dpi มักเกี่ยวข้องกับ PPI ในขณะที่ทั้งสองมีความแตกต่างกัน DPI หรือจุดต่อนิ้วเป็นการวัดความละเอียดเชิงพื้นที่ของเครื่องพิมพ์ ในกรณีของเครื่องพิมพ์ dpi หมายถึงจำนวนจุดหมึกที่พิมพ์ต่อนิ้วเมื่อพิมพ์ภาพออกจากเครื่องพิมพ์
อย่าลืมว่าแต่ละพิกเซลต่อนิ้วไม่จำเป็นต้องพิมพ์ทีละจุดต่อนิ้ว อาจมีหลายจุดต่อนิ้วที่ใช้สำหรับการพิมพ์หนึ่งพิกเซล สาเหตุที่เครื่องพิมพ์สีส่วนใหญ่ใช้รุ่น CMYK สีมีจำนวน จำกัด เครื่องพิมพ์มีให้เลือกจากสีเหล่านี้เพื่อสร้างสีของพิกเซลในขณะที่ในพีซีคุณมีสีหลายแสนสี
ยิ่งค่า dpi ของเครื่องพิมพ์สูงเท่าใดคุณภาพของเอกสารที่พิมพ์หรือภาพบนกระดาษก็จะยิ่งสูงขึ้นเท่านั้น
โดยปกติเครื่องพิมพ์เลเซอร์บางรุ่นจะมี dpi ที่ 300 และบางรุ่นมี 600 หรือมากกว่า
เส้นต่อนิ้ว
เมื่อ dpi หมายถึงจุดต่อนิ้วซับต่อนิ้วหมายถึงเส้นของจุดต่อนิ้ว ความละเอียดของหน้าจอ halftone วัดเป็นเส้นต่อนิ้ว
ตารางต่อไปนี้แสดงความจุบรรทัดต่อนิ้วของเครื่องพิมพ์
| เครื่องพิมพ์ | LPI |
|---|---|
| การพิมพ์สกรีน | 45-65 lpi |
| เครื่องพิมพ์เลเซอร์ (300 dpi) | 65 lpi |
| เครื่องพิมพ์เลเซอร์ (600 dpi) | 85-105 lpi |
| Offset Press (กระดาษหนังสือพิมพ์) | 85 lpi |
| Offset Press (กระดาษเคลือบ) | 85-185 lpi |
ความละเอียดของภาพ:
ความละเอียดระดับสีเทา:
ความละเอียดระดับสีเทาหมายถึงการเปลี่ยนแปลงที่คาดเดาได้หรือกำหนดได้ในเฉดสีหรือระดับสีเทาในรูปภาพ
ในความละเอียดระดับสีเทาสั้น ๆ จะเท่ากับจำนวนบิตต่อพิกเซล
เราได้พูดถึงบิตต่อพิกเซลแล้วในบทช่วยสอนเกี่ยวกับบิตต่อพิกเซลและข้อกำหนดในการจัดเก็บภาพ เราจะกำหนด bpp ที่นี่สั้น ๆ
BPP:
จำนวนสีที่แตกต่างกันในภาพขึ้นอยู่กับความลึกของสีหรือบิตต่อพิกเซล
ทางคณิตศาสตร์:
ความสัมพันธ์ทางคณิตศาสตร์ที่สามารถสร้างขึ้นระหว่างความละเอียดระดับสีเทาและบิตต่อพิกเซลสามารถกำหนดเป็น

ในสมการนี้ L หมายถึงจำนวนระดับสีเทา นอกจากนี้ยังสามารถกำหนดเป็นเฉดสีเทา และ k หมายถึง bpp หรือบิตต่อพิกเซล ดังนั้น 2 ยกกำลังของบิตต่อพิกเซลเท่ากับความละเอียดระดับสีเทา
ตัวอย่างเช่น:

ภาพไอน์สไตน์ด้านบนนี้เป็นภาพสเกลสีเทา หมายถึงภาพที่มี 8 บิตต่อพิกเซลหรือ 8bpp
ตอนนี้ถ้าจะคำนวณความละเอียดระดับสีเทาเราจะทำอย่างไร
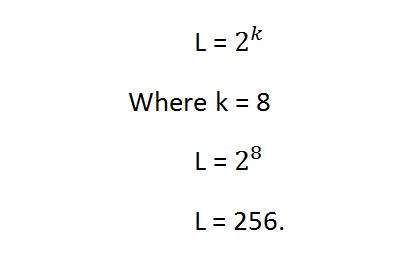
หมายความว่าความละเอียดระดับสีเทาคือ 256 หรืออีกนัยหนึ่งเราสามารถพูดได้ว่าภาพนี้มีเฉดสีเทาที่แตกต่างกัน 256 เฉด
ยิ่งมีจำนวนบิตต่อพิกเซลของภาพมากเท่าใดความละเอียดระดับสีเทาก็ยิ่งมากขึ้นเท่านั้น
การกำหนดความละเอียดระดับสีเทาในแง่ของ bpp:
ไม่จำเป็นว่าควรกำหนดความละเอียดระดับสีเทาในรูปของระดับเท่านั้น เรายังกำหนดเป็นบิตต่อพิกเซลได้อีกด้วย
ตัวอย่างเช่น:
หากคุณได้รับภาพ 4 bpp และระบบจะขอให้คุณคำนวณความละเอียดระดับสีเทา มีสองคำตอบสำหรับคำถามนั้น
คำตอบแรกคือ 16 ระดับ
คำตอบที่สองคือ 4 บิต
ค้นหา bpp จากความละเอียดระดับสีเทา:
คุณยังสามารถค้นหาบิตต่อพิกเซลได้จากความละเอียดระดับสีเทาที่กำหนด สำหรับสิ่งนี้เราต้องบิดสูตรเล็กน้อย
สมการ 1.

สูตรนี้ค้นหาระดับ ทีนี้ถ้าเราหาบิตต่อพิกเซลหรือในกรณีนี้ k เราก็จะเปลี่ยนเป็นแบบนี้
K = log ฐาน 2 (L) สมการ (2)
เนื่องจากในสมการแรกความสัมพันธ์ระหว่างระดับ (L) และบิตต่อพิกเซล (k) เป็นเลขชี้กำลัง ตอนนี้เราต้องเปลี่ยนกลับดังนั้นสิ่งที่ผกผันของเลขชี้กำลังคือ log
มาดูตัวอย่างเพื่อค้นหาบิตต่อพิกเซลจากความละเอียดระดับสีเทา
ตัวอย่างเช่น:
หากคุณได้รับภาพ 256 ระดับ บิตต่อพิกเซลที่จำเป็นสำหรับมันคืออะไร
เราใส่ 256 ในสมการ
K = ฐานบันทึก 2 (256)
K = 8.
ดังนั้นคำตอบคือ 8 บิตต่อพิกเซล
ความละเอียดระดับสีเทาและการหาปริมาณ:
การหาปริมาณจะถูกนำมาใช้อย่างเป็นทางการในบทช่วยสอนถัดไป แต่ในที่นี้เราจะอธิบายถึงความสัมพันธ์ระหว่างความละเอียดระดับสีเทาและการหาปริมาณ
พบความละเอียดระดับสีเทาบนแกน y ของสัญญาณ ในบทแนะนำเกี่ยวกับความรู้เบื้องต้นเกี่ยวกับสัญญาณและระบบเราได้ศึกษาว่าการแปลงสัญญาณอนาล็อกเป็นดิจิทัลต้องใช้สองขั้นตอน การสุ่มตัวอย่างและการหาปริมาณ

ทำการสุ่มตัวอย่างบนแกน x และการหาปริมาณจะทำในแกน Y
นั่นหมายถึงการแปลงความละเอียดระดับสีเทาของภาพให้เป็นดิจิทัลจะทำในการหาปริมาณ
เราได้แนะนำการหาปริมาณในการสอนสัญญาณและระบบของเรา เราจะเชื่อมโยงอย่างเป็นทางการกับภาพดิจิทัลในบทช่วยสอนนี้ มาพูดคุยกันก่อนเล็กน้อยเกี่ยวกับการหาปริมาณ
การแปลงสัญญาณเป็นดิจิทัล
ดังที่เราได้เห็นในบทช่วยสอนก่อนหน้านี้การแปลงสัญญาณแอนะล็อกให้เป็นดิจิทัลนั้นต้องใช้สองขั้นตอนพื้นฐาน การสุ่มตัวอย่างและการหาปริมาณ ทำการสุ่มตัวอย่างบนแกน x เป็นการแปลงแกน x (ค่าอนันต์) เป็นค่าดิจิทัล
รูปด้านล่างแสดงการสุ่มตัวอย่างสัญญาณ

การสุ่มตัวอย่างที่สัมพันธ์กับภาพดิจิทัล:
แนวคิดของการสุ่มตัวอย่างเกี่ยวข้องโดยตรงกับการซูม ยิ่งคุณใช้ตัวอย่างมากเท่าไหร่คุณก็จะได้พิกเซลมากขึ้นเท่านั้น การสุ่มตัวอย่างเกินสามารถเรียกได้ว่าเป็นการซูม สิ่งนี้ได้รับการกล่าวถึงภายใต้การสอนการสุ่มตัวอย่างและการซูม
แต่เรื่องราวของการแปลงสัญญาณดิจิทัลไม่ได้จบลงที่การสุ่มตัวอย่างเช่นกันยังมีอีกขั้นตอนที่เกี่ยวข้องซึ่งเรียกว่า Quantization
Quantization คืออะไร
Quantization ตรงข้ามกับการสุ่มตัวอย่าง มันทำบนแกน y เมื่อคุณกำลังปรับขนาดรูปภาพคุณกำลังแบ่งสัญญาณออกเป็นควอนต้า (พาร์ติชัน)
บนแกน x ของสัญญาณคือค่าพิกัดและบนแกน y เรามีแอมพลิจูด ดังนั้นการแปลงแอมพลิจูดให้เป็นดิจิทัลจึงเรียกว่า Quantization
นี่คือวิธีการทำ

คุณจะเห็นในภาพนี้ว่าสัญญาณได้รับการวัดปริมาณออกเป็นสามระดับที่แตกต่างกัน นั่นหมายความว่าเมื่อเราสุ่มตัวอย่างรูปภาพเรารวบรวมค่าต่างๆมากมายและในการหาปริมาณเราตั้งค่าระดับให้กับค่าเหล่านี้ สิ่งนี้สามารถชัดเจนมากขึ้นในภาพด้านล่าง
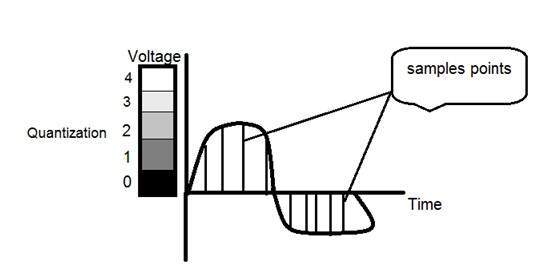
ในรูปที่แสดงในการสุ่มตัวอย่างแม้ว่าตัวอย่างจะถูกนำไปแล้ว แต่ก็ยังคงทอดในแนวตั้งไปยังช่วงของค่าระดับสีเทาอย่างต่อเนื่อง ในรูปที่แสดงด้านบนค่าที่เรียงตามแนวตั้งเหล่านี้ได้รับการวัดปริมาณออกเป็น 5 ระดับหรือพาร์ติชันที่แตกต่างกัน ตั้งแต่ 0 ดำไปจนถึง 4 ขาว ระดับนี้อาจแตกต่างกันไปตามประเภทของภาพที่คุณต้องการ
ความสัมพันธ์ของการหาปริมาณกับระดับสีเทาได้รับการกล่าวถึงเพิ่มเติมด้านล่าง
ความสัมพันธ์ของปริมาณที่มีความละเอียดระดับสีเทา:
ตัวเลขเชิงปริมาณที่แสดงด้านบนมีระดับสีเทา 5 ระดับ หมายความว่าภาพที่เกิดจากสัญญาณนี้จะมีสีต่างกันเพียง 5 สี มันจะเป็นภาพขาวดำไม่มากก็น้อยที่มีสีเทาบ้าง ตอนนี้ถ้าคุณต้องการปรับปรุงคุณภาพของภาพให้ดีขึ้นมีสิ่งหนึ่งที่คุณสามารถทำได้ที่นี่ ซึ่งก็คือการเพิ่มระดับหรือความละเอียดระดับสีเทาขึ้น หากคุณเพิ่มระดับนี้เป็น 256 แสดงว่าคุณมีภาพระดับสีเทา ซึ่งดีกว่ามากแล้วภาพขาวดำเรียบง่าย
ตอนนี้ 256 หรือ 5 หรือระดับที่คุณเคยเลือกเรียกว่าระดับสีเทา จำสูตรที่เราพูดถึงในบทช่วยสอนก่อนหน้าเกี่ยวกับความละเอียดระดับสีเทาซึ่งก็คือ

เราได้หารือกันว่าระดับสีเทาสามารถกำหนดได้สองวิธี ซึ่งเป็นสองคนนี้
ระดับสีเทา = จำนวนบิตต่อพิกเซล (BPP) (k ในสมการ)
ระดับสีเทา = จำนวนระดับต่อพิกเซล
ในกรณีนี้เรามีระดับสีเทาเท่ากับ 256 ถ้าเราต้องคำนวณจำนวนบิตเราก็ใส่ค่าลงในสมการ ในกรณีของ 256 ระดับเรามีเฉดสีเทา 256 เฉดและ 8 บิตต่อพิกเซลดังนั้นภาพจึงเป็นภาพระดับสีเทา
ลดระดับสีเทา
ตอนนี้เราจะลดระดับสีเทาของภาพเพื่อดูเอฟเฟกต์บนภาพ
ตัวอย่างเช่น:
สมมติว่าคุณมีรูปภาพของ 8bpp ซึ่งมีระดับที่แตกต่างกัน 256 ระดับ มันเป็นภาพโทนสีเทาและภาพจะมีลักษณะประมาณนี้
256 ระดับสีเทา

ตอนนี้เราจะเริ่มลดระดับสีเทา ก่อนอื่นเราจะลดระดับสีเทาจาก 256 เป็น 128
128 ระดับสีเทา

ไม่มีผลต่อภาพมากนักหลังจากลดระดับสีเทาลงเหลือครึ่งหนึ่ง ให้ลดลงบ้าง
64 ระดับสีเทา

ยังไม่มีผลมากนักจากนั้นให้ลดระดับมากขึ้น
32 ระดับสีเทา

ประหลาดใจที่เห็นว่ายังมีผลเล็กน้อย อาจเป็นเพราะเหตุผลนั่นคือภาพของไอน์สไตน์ แต่ช่วยลดระดับให้มากขึ้น
16 ระดับสีเทา

บูมที่นี่เราไปในที่สุดภาพก็เผยให้เห็นว่ามันได้รับผลกระทบจากระดับ
8 ระดับสีเทา

4 ระดับสีเทา

ตอนนี้ก่อนที่จะลดลงอีก 2 ระดับคุณจะเห็นได้อย่างง่ายดายว่าภาพบิดเบี้ยวไม่ดีโดยการลดระดับสีเทา ตอนนี้เราจะลดเป็น 2 ระดับซึ่งไม่มีอะไรนอกจากระดับขาวดำธรรมดา หมายความว่าภาพจะเป็นภาพขาวดำธรรมดา ๆ
2 ระดับสีเทา

นั่นคือระดับสุดท้ายที่เราทำได้เพราะถ้าลดลงไปอีกมันจะเป็นเพียงภาพสีดำซึ่งไม่สามารถตีความได้
Contouring:
มีข้อสังเกตที่น่าสนใจคือเมื่อเราลดจำนวนระดับสีเทาจะมีเอฟเฟกต์พิเศษปรากฏขึ้นในภาพซึ่งสามารถมองเห็นได้ชัดเจนในภาพระดับสีเทา 16 ภาพ เอฟเฟกต์นี้เรียกว่า Contouring
เส้นโค้งการตั้งค่า ISO:
คำตอบของเอฟเฟกต์นี้ว่าเหตุใดจึงปรากฏอยู่ในเส้นโค้งการตั้งค่า Iso พวกเขาจะกล่าวถึงในบทแนะนำต่อไปของเส้นโค้งการตั้งค่า Contouring และ Iso
Contouring คืออะไร?
เมื่อเราลดจำนวนระดับสีเทาในภาพสีหรือขอบที่ผิดพลาดบางส่วนจะเริ่มปรากฏบนภาพ สิ่งนี้ได้แสดงไว้ในบทช่วยสอนสุดท้ายของ Quantization
มาดูกันเลย
ลองพิจารณาเรามีภาพ 8bpp (ภาพระดับสีเทา) ที่มีระดับสีเทาหรือสีเทา 256 เฉด

ภาพด้านบนนี้มีเฉดสีเทาที่แตกต่างกัน 256 เฉด ตอนนี้เมื่อเราลดเป็น 128 และลดอีก 64 ภาพจะมากหรือน้อยเท่ากัน แต่เมื่อลดระดับลงไปอีก 32 ระดับเราได้ภาพแบบนี้

หากคุณมองอย่างใกล้ชิดคุณจะพบว่าเอฟเฟกต์เริ่มปรากฏบนภาพเอฟเฟกต์เหล่านี้จะมองเห็นได้ชัดเจนขึ้นเมื่อเราลดระดับลงไปอีก 16 ระดับและเราได้ภาพเช่นนี้

เส้นเหล่านี้ที่เริ่มปรากฏบนภาพนี้เรียกว่าเส้นขอบที่มองเห็นได้ชัดเจนในภาพด้านบน
เพิ่มและลดรูปร่าง
ผลของการสร้างเส้นขอบจะเพิ่มขึ้นเมื่อเราลดจำนวนระดับสีเทาและผลจะลดลงเมื่อเราเพิ่มจำนวนระดับสีเทา พวกเขาทั้งสองในทางกลับกัน

VS

นั่นหมายถึงการหาปริมาณที่มากขึ้นจะมีผลในรูปทรงมากขึ้นและในทางกลับกัน แต่เป็นเช่นนี้เสมอ คำตอบคือไม่ขึ้นอยู่กับสิ่งอื่นที่กล่าวถึงด้านล่าง
เส้นโค้ง Isopreference
การศึกษาที่ดำเนินการเกี่ยวกับผลกระทบของระดับสีเทาและรูปร่างและผลลัพธ์แสดงในรูปแบบของกราฟในรูปแบบของเส้นโค้งหรือที่เรียกว่าเส้นโค้งค่ากำหนด Iso
ปรากฏการณ์ของเส้นโค้งแบบ Isopreference แสดงให้เห็นว่าผลของเส้นโครงร่างไม่เพียงขึ้นอยู่กับการลดลงของความละเอียดระดับสีเทา แต่ยังขึ้นอยู่กับรายละเอียดของภาพด้วย
สาระสำคัญของการศึกษาคือ:
หากภาพมีรายละเอียดมากขึ้นผลของเส้นโครงร่างจะเริ่มปรากฏในภาพนี้ในภายหลังเมื่อเปรียบเทียบกับภาพที่มีรายละเอียดน้อยกว่าเมื่อมีการวัดระดับสีเทา
จากการวิจัยต้นฉบับนักวิจัยได้ถ่ายภาพทั้งสามภาพนี้และปรับความละเอียดระดับสีเทาในทั้งสามภาพ
ภาพเป็น



ระดับของรายละเอียด:
ภาพแรกมีเพียงใบหน้าเท่านั้นจึงมีรายละเอียดน้อยมาก ภาพที่สองมีวัตถุอื่น ๆ ในภาพด้วยเช่นกล้องถ่ายรูปขาตั้งกล้องและวัตถุพื้นหลังเป็นต้นในขณะที่ภาพที่สามมีรายละเอียดมากกว่าภาพอื่น ๆ ทั้งหมด
การทดลอง:
ความละเอียดระดับสีเทานั้นแตกต่างกันไปในทุกภาพและขอให้ผู้ชมให้คะแนนทั้งสามภาพนี้ตามอัตวิสัย หลังจากการจัดอันดับกราฟจะถูกวาดตามผลลัพธ์
ผลลัพธ์:
ผลลัพธ์ถูกวาดบนกราฟ เส้นโค้งแต่ละเส้นบนกราฟแสดงภาพเดียว ค่าบนแกน x แสดงถึงจำนวนระดับสีเทาและค่าบนแกน y แทนบิตต่อพิกเซล (k)
กราฟได้แสดงไว้ด้านล่าง
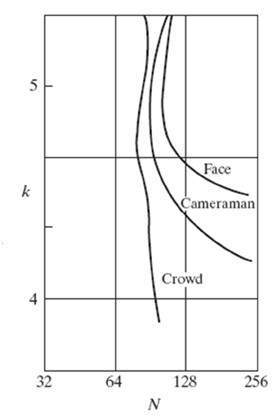
จากกราฟนี้เราจะเห็นว่าภาพแรกซึ่งเป็นใบหน้าอยู่ภายใต้เส้นโครงร่างในช่วงต้นจากนั้นอีกสองภาพทั้งหมด ภาพที่สองซึ่งเป็นของตากล้องจะต้องมีเส้นโครงร่างเล็กน้อยหลังจากภาพแรกเมื่อระดับสีเทาลดลง เนื่องจากมีรายละเอียดมากกว่าภาพแรก และภาพที่สามอาจมีรูปร่างมากหลังจากสองภาพแรกคือ: หลังจาก 4 bpp เนื่องจากภาพนี้มีรายละเอียดมากขึ้น
สรุป:
ดังนั้นสำหรับภาพที่มีรายละเอียดมากขึ้นเส้นโค้ง isopreference จึงเป็นแนวตั้งมากขึ้นเรื่อย ๆ นอกจากนี้ยังหมายความว่าสำหรับภาพที่มีรายละเอียดจำนวนมากจำเป็นต้องมีระดับสีเทาน้อยมาก
ในบทช่วยสอนเรื่อง Quantization และ Contouring สองบทที่ผ่านมาเราพบว่าการลดระดับสีเทาของรูปภาพจะช่วยลดจำนวนสีที่ต้องใช้ในการแสดงภาพ หากระดับสีเทาลดลง 2 2 ภาพที่ปรากฏจะไม่มีความละเอียดเชิงพื้นที่มากนักหรือไม่น่าสนใจมากนัก
Dithering:
Dithering เป็นกระบวนการที่เราสร้างภาพลวงตาของสีที่ไม่มีอยู่จริง ทำได้โดยการจัดเรียงพิกเซลแบบสุ่ม
ตัวอย่างเช่น. ลองพิจารณาภาพนี้

นี่คือภาพที่มีพิกเซลขาวดำเท่านั้น พิกเซลของมันถูกจัดเรียงตามลำดับเพื่อสร้างภาพอื่นที่แสดงด้านล่าง หมายเหตุเกี่ยวกับการจัดเรียงของพิกเซลมีการเปลี่ยนแปลง แต่ไม่ใช่จำนวนพิกเซล

ทำไมต้อง Dithering?
ทำไมเราถึงต้องการการแยกส่วนคำตอบของสิ่งนี้อยู่ที่ความสัมพันธ์กับการหาปริมาณ
Dithering กับ quantization
เมื่อเราทำการวัดปริมาณจนถึงระดับสุดท้ายเราจะเห็นว่าภาพที่มาในระดับสุดท้าย (ระดับ 2) มีลักษณะเช่นนี้

ตอนนี้อย่างที่เราเห็นจากภาพตรงนี้ว่าภาพยังไม่ชัดเจนนักโดยเฉพาะอย่างยิ่งถ้าคุณจะดูที่แขนซ้ายและด้านหลังของภาพของไอน์สไตน์ นอกจากนี้ภาพนี้ยังไม่มีข้อมูลหรือรายละเอียดเกี่ยวกับ Einstein มากนัก
ตอนนี้ถ้าเราจะเปลี่ยนภาพนี้เป็นภาพที่ให้รายละเอียดมากกว่านี้เราต้องทำการแยก
กำลังทำการ dithering
ก่อนอื่นเราจะดำเนินการเกี่ยวกับการเกณฑ์ โดยปกติ Dithering จะทำงานเพื่อปรับปรุงขีด จำกัด ในระหว่างการขีด จำกัด ขอบคมจะปรากฏขึ้นโดยที่การไล่ระดับสีจะราบรื่นในภาพ
ในการกำหนดเกณฑ์เราเพียงแค่เลือกค่าคงที่ พิกเซลทั้งหมดที่อยู่เหนือค่านั้นถือเป็น 1 และค่าทั้งหมดที่อยู่ด้านล่างจะถือเป็น 0
เราได้ภาพนี้หลังจากขีด จำกัด

เนื่องจากภาพนี้ไม่มีการเปลี่ยนแปลงมากนักเนื่องจากค่าเป็น 0 และ 1 หรือขาวดำในภาพนี้อยู่แล้ว
ตอนนี้เราทำการสุ่ม dithering กับมัน การจัดเรียงพิกเซลแบบสุ่ม

เราได้ภาพที่ให้รายละเอียดมากขึ้น แต่คอนทราสต์ต่ำมาก
เราจึงทำการแยกส่วนเพิ่มเติมเพื่อเพิ่มความเปรียบต่าง ภาพที่เราได้คือ:

ตอนนี้เราผสมผสานแนวคิดของการแบ่งแบบสุ่มพร้อมกับเกณฑ์และเราได้ภาพแบบนี้

ตอนนี้คุณเห็นแล้วเราได้ภาพเหล่านี้ทั้งหมดเพียงแค่จัดเรียงพิกเซลของภาพใหม่ การจัดเรียงใหม่นี้อาจเป็นการสุ่มหรืออาจเป็นไปตามมาตรการบางอย่าง
ก่อนที่จะพูดถึงการใช้ฮิสโตแกรมในการประมวลผลภาพเราจะมาดูกันก่อนว่าฮิสโตแกรมคืออะไรใช้อย่างไรจากนั้นจึงเป็นตัวอย่างของฮิสโตแกรมเพื่อให้เข้าใจฮิสโตแกรมมากขึ้น
ฮิสโตแกรม:
ฮิสโตแกรมคือกราฟ กราฟที่แสดงความถี่ของสิ่งใด ๆ โดยปกติแล้วฮิสโตแกรมจะมีแถบที่แสดงถึงความถี่ของการเกิดข้อมูลในชุดข้อมูลทั้งหมด
ฮิสโตแกรมมีสองแกนคือแกน x และแกน y
แกน x ประกอบด้วยเหตุการณ์ที่คุณต้องนับความถี่
แกน y ประกอบด้วยความถี่
ความสูงที่แตกต่างกันของแถบแสดงความถี่ของการเกิดข้อมูลที่แตกต่างกัน
โดยปกติฮิสโตแกรมจะมีลักษณะเช่นนี้
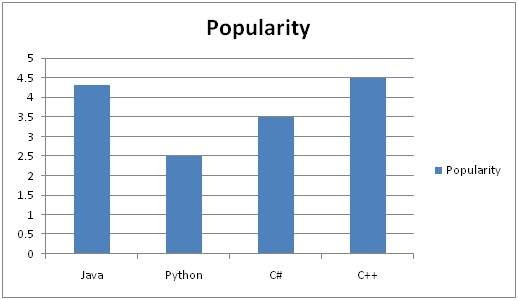
ตอนนี้เราจะเห็นตัวอย่างของฮิสโตแกรมนี้คือการสร้าง
ตัวอย่าง:
พิจารณาชั้นเรียนของนักเรียนเขียนโปรแกรมและคุณกำลังสอน Python ให้พวกเขา
ในตอนท้ายของภาคการศึกษาคุณจะได้ผลลัพธ์ที่แสดงในตาราง แต่มันยุ่งมากและไม่แสดงผลการเรียนโดยรวมของคุณ ดังนั้นคุณต้องสร้างฮิสโตแกรมของผลลัพธ์ของคุณเพื่อแสดงความถี่โดยรวมของการเกิดเกรดในชั้นเรียนของคุณ นี่คือวิธีที่คุณจะทำ
ใบแสดงผล:
| ชื่อ | เกรด |
|---|---|
| จอห์น | ก |
| แจ็ค | ง |
| คาร์เตอร์ | ข |
| ทอมมี่ | ก |
| ลิซ่า | C + |
| เดเร็ค | ก - |
| ทอม | B + |
ฮิสโตแกรมของแผ่นผลลัพธ์:
ตอนนี้สิ่งที่คุณจะทำคือคุณต้องหาสิ่งที่อยู่บนแกน x และแกน y
มีสิ่งหนึ่งที่ต้องแน่ใจคือแกน y นั้นมีความถี่ดังนั้นสิ่งที่อยู่บนแกน x แกน X ประกอบด้วยเหตุการณ์ที่ต้องคำนวณความถี่ ในกรณีนี้แกน x มีเกรด
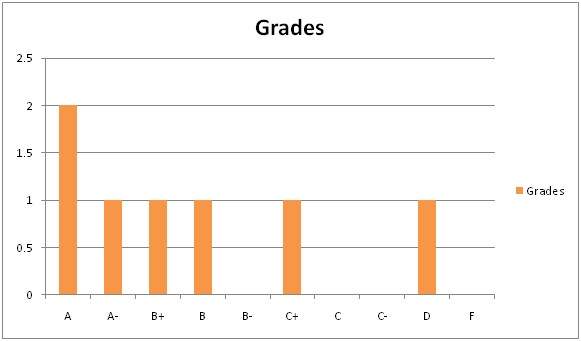
ตอนนี้เราจะใช้ฮิสโตแกรมในภาพอย่างไร
ฮิสโตแกรมของรูปภาพ
ฮิสโตแกรมของรูปภาพเช่นเดียวกับฮิสโตแกรมอื่น ๆ ก็แสดงความถี่เช่นกัน แต่ฮิสโตแกรมภาพแสดงความถี่ของค่าความเข้มของพิกเซล ในฮิสโตแกรมรูปภาพแกน x จะแสดงความเข้มของระดับสีเทาและแกน y จะแสดงความถี่ของความเข้มเหล่านี้
ตัวอย่างเช่น:

ฮิสโตแกรมของภาพด้านบนของไอน์สไตน์จะเป็นแบบนี้
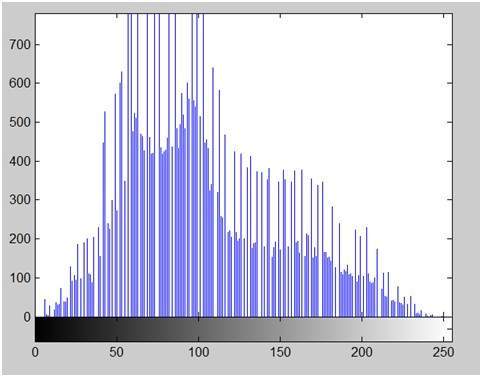
แกน x ของฮิสโตแกรมแสดงช่วงของค่าพิกเซล เนื่องจากเป็นภาพขนาด 8 bpp นั่นหมายความว่ามีสีเทา 256 ระดับหรือเฉดสีเทาอยู่ในนั้น นั่นคือสาเหตุที่ช่วงของแกน x เริ่มจาก 0 และสิ้นสุดที่ 255 โดยมีช่องว่าง 50 ในขณะที่แกน y คือจำนวนความเข้มเหล่านี้
ดังที่คุณเห็นจากกราฟแท่งส่วนใหญ่ที่มีความถี่สูงจะอยู่ในส่วนครึ่งแรกซึ่งเป็นส่วนที่มืดกว่า นั่นหมายความว่าภาพที่เราได้นั้นมืดลง และสิ่งนี้สามารถพิสูจน์ได้จากภาพด้วย
การใช้ฮิสโตแกรม:
ฮิสโตแกรมมีประโยชน์มากมายในการประมวลผลภาพ การใช้งานครั้งแรกตามที่ได้กล่าวไว้ข้างต้นคือการวิเคราะห์ภาพ เราสามารถคาดเดาเกี่ยวกับรูปภาพได้โดยดูที่ฮิสโตแกรม มันเหมือนกับการเอ็กซเรย์กระดูกของร่างกาย
การใช้ฮิสโตแกรมครั้งที่สองมีวัตถุประสงค์เพื่อความสว่าง ฮิสโตแกรมมีการใช้งานที่กว้างในความสว่างของภาพ ไม่เพียง แต่ในความสว่างเท่านั้น แต่ยังใช้ฮิสโทแกรมในการปรับคอนทราสต์ของภาพอีกด้วย
การใช้ฮิสโตแกรมที่สำคัญอีกประการหนึ่งคือการทำให้ภาพเท่ากัน
และสุดท้าย แต่ไม่ท้ายสุดฮิสโตแกรมมีประโยชน์อย่างกว้างขวางในการกำหนดเกณฑ์ ส่วนใหญ่จะใช้ในการมองเห็นด้วยคอมพิวเตอร์
ความสว่าง:
ความสว่างเป็นคำที่สัมพันธ์กัน ขึ้นอยู่กับการรับรู้ภาพของคุณ เนื่องจากความสว่างเป็นคำที่สัมพันธ์กันดังนั้นความสว่างจึงสามารถกำหนดเป็นปริมาณพลังงานที่ส่งออกโดยแหล่งกำเนิดแสงที่สัมพันธ์กับแหล่งกำเนิดที่เราเปรียบเทียบ ในบางกรณีเราสามารถพูดได้ง่ายๆว่าภาพสว่างและในบางกรณีการรับรู้ไม่ใช่เรื่องง่าย
ตัวอย่างเช่น:
เพียงแค่ดูทั้งสองภาพนี้แล้วเปรียบเทียบว่าภาพใดสว่างกว่ากัน

เราจะเห็นได้ง่ายว่าภาพทางด้านขวาจะสว่างกว่าเมื่อเทียบกับภาพทางซ้าย
แต่ถ้าภาพด้านขวาทำให้มืดกว่าภาพแรกเราก็บอกได้ว่าภาพด้านซ้ายสว่างกว่าด้านซ้าย
วิธีทำให้ภาพสว่างขึ้น
ความสว่างสามารถเพิ่มหรือลดได้เพียงแค่การบวกหรือการลบอย่างง่ายในเมทริกซ์ภาพ
พิจารณาภาพสีดำ 5 แถวและ 5 คอลัมน์

เนื่องจากเราทราบแล้วว่าแต่ละภาพมีเมทริกซ์ที่ด้านหลังซึ่งมีค่าพิกเซล เมทริกซ์ภาพนี้ได้รับด้านล่าง
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
เนื่องจากเมทริกซ์ทั้งหมดเต็มไปด้วยศูนย์และภาพจึงมืดลงมาก
ตอนนี้เราจะเปรียบเทียบกับภาพสีดำอื่น ๆ เพื่อดูว่าภาพนี้สว่างขึ้นหรือไม่

ยังคงเหมือนกันทั้งสองภาพตอนนี้เราจะดำเนินการบางอย่างกับ image1 เนื่องจากภาพที่สองจะสว่างขึ้น
สิ่งที่เราจะทำก็คือเราจะเพิ่มค่า 1 ให้กับแต่ละค่าเมทริกซ์ของรูปภาพ 1 หลังจากเพิ่มรูปภาพ 1 แล้วจะได้อะไรประมาณนี้

ตอนนี้เราจะเปรียบเทียบกับภาพที่ 2 อีกครั้งและดูความแตกต่าง

เราเห็นว่ายังไม่สามารถบอกได้ว่าภาพใดสว่างขึ้นเนื่องจากทั้งสองภาพมีลักษณะเหมือนกัน
ตอนนี้สิ่งที่เราจะทำคือเราจะเพิ่ม 50 ให้กับแต่ละค่าเมทริกซ์ของรูปภาพ 1 และดูว่าภาพนั้นกลายเป็นอย่างไร
ผลลัพธ์จะได้รับด้านล่าง

อีกครั้งเราจะเปรียบเทียบกับภาพที่ 2
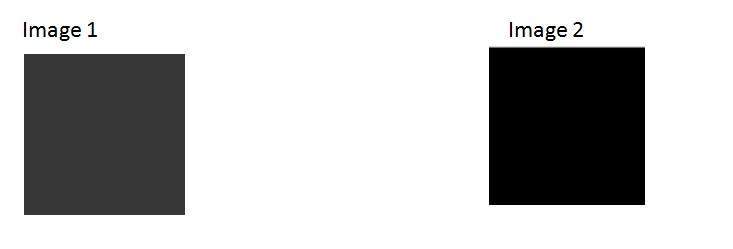
ตอนนี้คุณจะเห็นว่าภาพที่ 1 สว่างขึ้นเล็กน้อยจากนั้นภาพที่ 2 เราไปต่อและเพิ่มอีก 45 ค่าให้กับเมทริกซ์ของภาพ 1 และคราวนี้เราจะเปรียบเทียบทั้งสองภาพอีกครั้ง

ตอนนี้เมื่อคุณเปรียบเทียบคุณจะเห็นว่าภาพนี้ 1 สว่างกว่าภาพ 2 อย่างชัดเจน
แม้จะสว่างกว่าแล้วก็ตามภาพเก่า 1. ณ จุดนี้เมทริกซ์ของอิมเมจ 1 มี 100 ในแต่ละดัชนีเมื่อเพิ่มครั้งแรก 5 จากนั้น 50 แล้ว 45 ดังนั้น 5 + 50 + 45 = 100
ความคมชัด
คอนทราสต์สามารถอธิบายได้ง่ายๆว่าเป็นความแตกต่างระหว่างความเข้มพิกเซลสูงสุดและต่ำสุดในภาพ
ตัวอย่างเช่น.
พิจารณาภาพสุดท้าย 1 ด้วยความสว่าง

เมทริกซ์ของภาพนี้คือ:
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 |
ค่าสูงสุดในเมทริกซ์นี้คือ 100
ค่าต่ำสุดในเมทริกซ์นี้คือ 100
Contrast = ความเข้มพิกเซลสูงสุด (ลบด้วย) ความเข้มพิกเซลต่ำสุด
= 100 (ลบด้วย) 100
= 0
0 หมายความว่าภาพนี้มีความเปรียบต่าง 0
ก่อนที่เราจะพูดถึงการเปลี่ยนแปลงภาพคืออะไรเราจะพูดถึงการเปลี่ยนแปลงคืออะไร
การเปลี่ยนแปลง
การเปลี่ยนแปลงเป็นหน้าที่ ฟังก์ชันที่จับคู่ชุดหนึ่งกับอีกชุดหนึ่งหลังจากดำเนินการบางอย่าง
ระบบประมวลผลภาพดิจิตอล:
เราได้เห็นไปแล้วในบทแนะนำเบื้องต้นว่าในการประมวลผลภาพดิจิทัลเราจะพัฒนาระบบที่อินพุตจะเป็นรูปภาพและเอาต์พุตจะเป็นรูปภาพด้วย และระบบจะทำการประมวลผลภาพอินพุตและให้เอาต์พุตเป็นภาพที่ประมวลผล ดังแสดงด้านล่าง
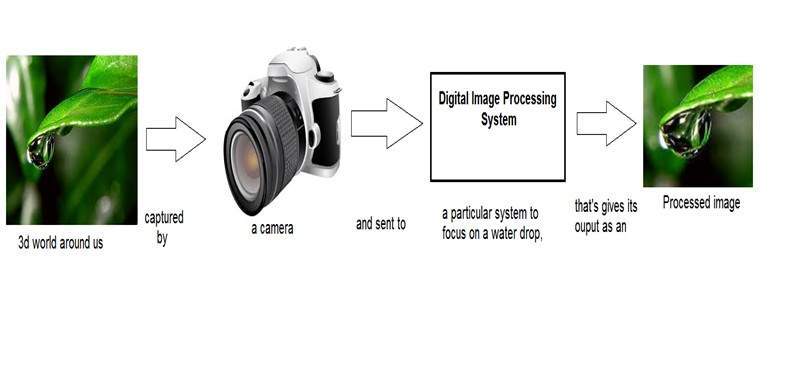
ฟังก์ชัน Now ที่ใช้ภายในระบบดิจิทัลนี้ซึ่งประมวลผลภาพและแปลงเป็นเอาต์พุตสามารถเรียกได้ว่าเป็นฟังก์ชันการแปลง
ตามที่แสดงการแปลงหรือความสัมพันธ์วิธีที่รูปภาพ 1 ถูกแปลงเป็นรูปภาพ 2
การเปลี่ยนแปลงรูปภาพ
พิจารณาสมการนี้
ก (x, y) = T {f (x, y)}
ในสมการนี้
F (x, y) = ภาพอินพุตที่ต้องใช้ฟังก์ชันการแปลง
G (x, y) = ภาพที่ส่งออกหรือภาพที่ประมวลผล
T คือฟังก์ชันการเปลี่ยนแปลง
ความสัมพันธ์ระหว่างอิมเมจอินพุตและอิมเมจเอาต์พุตที่ประมวลผลสามารถแสดงเป็น
s = T (r)
โดยที่ r คือค่าพิกเซลหรือความเข้มระดับสีเทาของ f (x, y) ณ จุดใด ๆ และ s คือค่าพิกเซลหรือความเข้มระดับสีเทาของ g (x, y) ณ จุดใด ๆ
การแปลงระดับสีเทาขั้นพื้นฐานได้รับการกล่าวถึงในบทช่วยสอนของเราเกี่ยวกับการแปลงระดับสีเทาขั้นพื้นฐาน
ตอนนี้เราจะพูดถึงฟังก์ชั่นการแปลงขั้นพื้นฐานบางอย่าง
ตัวอย่าง:
พิจารณาฟังก์ชันการเปลี่ยนแปลงนี้
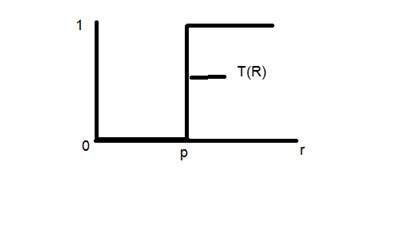
ให้จุด r เป็น 256 และจุด p เป็น 127 พิจารณาว่าภาพนี้เป็นภาพ bpp หนึ่งภาพ นั่นหมายความว่าเรามีความเข้มเพียง 2 ระดับนั่นคือ 0 และ 1 ดังนั้นในกรณีนี้การเปลี่ยนแปลงที่แสดงโดยกราฟสามารถอธิบายได้ว่า
ค่าความเข้มของพิกเซลทั้งหมดที่ต่ำกว่า 127 (จุด p) เป็น 0 หมายถึงสีดำ และค่าความเข้มของพิกเซลทั้งหมดที่มากกว่า 127 เป็น 1 นั่นหมายถึงสีขาว แต่เมื่อถึงจุด 127 มีการเปลี่ยนเกียร์กะทันหันดังนั้นเราจึงไม่สามารถบอกได้ว่า ณ จุดนั้นค่าจะเป็น 0 หรือ 1
ในทางคณิตศาสตร์ฟังก์ชันการเปลี่ยนแปลงนี้สามารถแสดงเป็น:
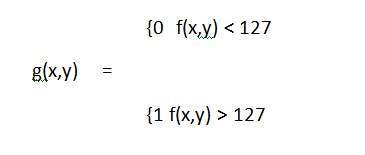
พิจารณาการเปลี่ยนแปลงอื่นเช่นนี้:
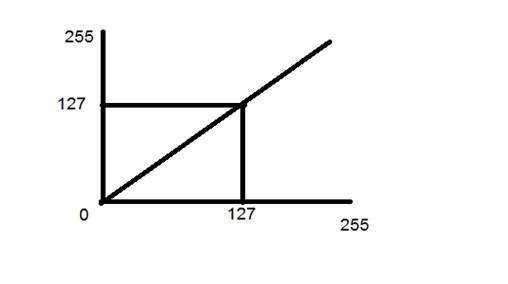
ตอนนี้ถ้าคุณจะดูกราฟนี้คุณจะเห็นเส้นตรงระหว่างภาพอินพุตและภาพเอาต์พุต
แสดงว่าสำหรับแต่ละพิกเซลหรือค่าความเข้มของภาพอินพุตมีค่าความเข้มของภาพที่ส่งออกเท่ากัน นั่นหมายความว่าภาพที่ส่งออกเป็นภาพจำลองที่แน่นอนของภาพอินพุต
สามารถแสดงทางคณิตศาสตร์เป็น:
ก. (x, y) = f (x, y)
ภาพอินพุตและเอาต์พุตจะอยู่ในกรณีนี้ดังแสดงด้านล่าง

แนวคิดพื้นฐานของฮิสโทแกรมได้รับการกล่าวถึงในบทแนะนำเกี่ยวกับฮิสโตแกรมเบื้องต้น แต่เราจะแนะนำฮิสโตแกรมสั้น ๆ ที่นี่
ฮิสโตแกรม:
ฮิสโตแกรมไม่ใช่อะไรนอกจากกราฟที่แสดงความถี่ของการเกิดข้อมูล ฮิสโตแกรมมีประโยชน์มากมายในการประมวลผลภาพซึ่งเราจะพูดถึงผู้ใช้รายหนึ่งที่นี่ซึ่งเรียกว่าการเลื่อนแบบฮิสโตแกรม
ฮิสโตแกรมเลื่อน
ในการเลื่อนฮิสโตแกรมเราเพียงแค่เลื่อนฮิสโตแกรมทั้งหมดไปทางขวาหรือซ้าย เนื่องจากการเลื่อนหรือเลื่อนของฮิสโตแกรมไปทางขวาหรือซ้ายทำให้สามารถเห็นการเปลี่ยนแปลงที่ชัดเจนในภาพได้ในบทช่วยสอนนี้เราจะใช้การเลื่อนฮิสโตแกรมเพื่อจัดการความสว่าง
คำว่า: ความสว่างได้รับการกล่าวถึงในบทแนะนำเกี่ยวกับความสว่างและความเปรียบต่าง แต่เราจะอธิบายสั้น ๆ ตรงนี้
ความสว่าง:
ความสว่างเป็นคำที่สัมพันธ์กัน ความสว่างสามารถกำหนดเป็นความเข้มของแสงที่ปล่อยออกมาจากแหล่งกำเนิดแสงเฉพาะ
ความคมชัด:
คอนทราสต์สามารถกำหนดให้เป็นความแตกต่างระหว่างความเข้มพิกเซลสูงสุดและต่ำสุดในรูปภาพ
ฮิสโตแกรมแบบเลื่อน
การเพิ่มความสว่างโดยใช้การเลื่อนฮิสโตแกรม

ฮิสโตแกรมของภาพนี้แสดงไว้ด้านล่าง
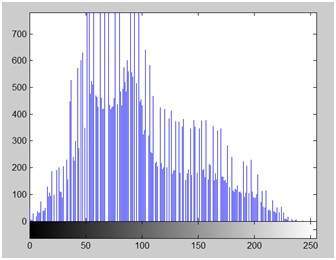
บนแกน y ของฮิสโตแกรมนี้คือความถี่หรือจำนวนนับ และบนแกน x เรามีค่าระดับสีเทา ดังที่คุณเห็นจากฮิสโตแกรมด้านบนความเข้มของระดับสีเทาเหล่านั้นที่มีจำนวนมากกว่า 700 อยู่ในส่วนครึ่งแรกหมายถึงส่วนที่ดำกว่า นั่นคือเหตุผลที่เราได้ภาพที่มืดกว่าเล็กน้อย
เพื่อให้มันสว่างขึ้นเราจะเลื่อนฮิสโตแกรมไปทางขวาหรือไปทางส่วนสีขาว ในการจะทำเราต้องเพิ่มค่าอย่างน้อย 50 ให้กับภาพนี้ เนื่องจากเราสามารถดูได้จากฮิสโตแกรมด้านบนว่าภาพนี้มีความเข้ม 0 พิกเซลด้วยซึ่งเป็นสีดำล้วน ดังนั้นถ้าเราเพิ่ม 0 ถึง 50 เราจะเปลี่ยนค่าทั้งหมดที่อยู่ที่ความเข้ม 0 เป็นความเข้ม 50 และค่าที่เหลือทั้งหมดจะเลื่อนตาม
มาทำกันเถอะ
สิ่งที่เราได้รับหลังจากเพิ่ม 50 ให้กับความเข้มของแต่ละพิกเซล
ภาพได้แสดงไว้ด้านล่าง

และฮิสโตแกรมได้แสดงไว้ด้านล่าง
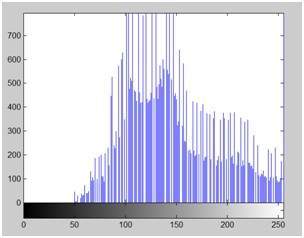
ให้เปรียบเทียบสองภาพนี้กับฮิสโทแกรมเพื่อดูว่าต้องมีการเปลี่ยนแปลงอะไรบ้าง
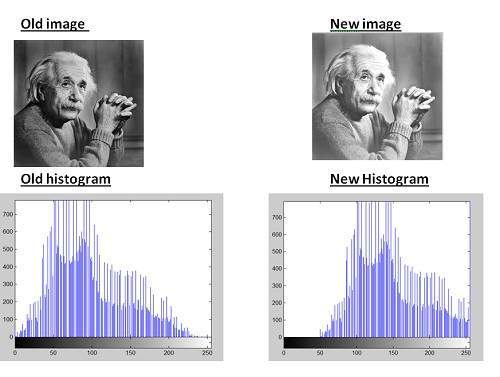
สรุป:
ดังที่เราเห็นได้อย่างชัดเจนจากฮิสโตแกรมใหม่ว่าค่าพิกเซลทั้งหมดถูกเลื่อนไปทางขวาและสามารถเห็นเอฟเฟกต์ของมันได้ในภาพใหม่
การลดความสว่างโดยใช้การเลื่อนฮิสโตแกรม
ตอนนี้ถ้าเราลดความสว่างของภาพใหม่ลงจนภาพเก่าดูสว่างขึ้นเราต้องลบค่าบางส่วนออกจากเมทริกซ์ทั้งหมดของภาพใหม่ ค่าที่เราจะลบคือ 80 เนื่องจากเราได้เพิ่ม 50 ลงในภาพต้นฉบับแล้วและเราได้ภาพใหม่ที่สว่างกว่าตอนนี้ถ้าเราต้องการให้มันมืดลงเราต้องลบออกอย่างน้อยมากกว่า 50
และนี่คือสิ่งที่เราได้หลังจากลบ 80 ออกจากรูปใหม่
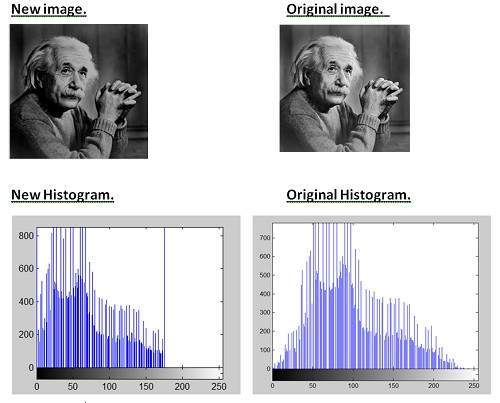
สรุป:
เห็นได้ชัดจากฮิสโตแกรมของภาพใหม่ว่าค่าพิกเซลทั้งหมดถูกเลื่อนไปทางขวาดังนั้นจึงสามารถตรวจสอบได้จากภาพว่าภาพใหม่มีสีเข้มขึ้นและตอนนี้ภาพต้นฉบับดูสว่างขึ้นเมื่อเทียบกับภาพใหม่นี้
ข้อดีอีกอย่างหนึ่งของ Histogram s ที่เราพูดถึงในบทแนะนำเกี่ยวกับฮิสโตแกรมคือการเพิ่มความเปรียบต่าง
มีสองวิธีในการเพิ่มความเปรียบต่าง อันแรกเรียกว่าการยืดฮิสโตแกรมที่เพิ่มคอนทราสต์ อันที่สองเรียกว่าการทำให้เท่าเทียมกันของฮิสโตแกรมซึ่งช่วยเพิ่มความเปรียบต่างและได้รับการกล่าวถึงในบทช่วยสอนเรื่องการทำให้เท่ากันฮิสโตแกรม
ก่อนที่เราจะพูดถึงการยืดฮิสโตแกรมเพื่อเพิ่มความคมชัดเราจะกำหนดคอนทราสต์สั้น ๆ
ความคมชัด
คอนทราสต์คือความแตกต่างระหว่างความเข้มพิกเซลสูงสุดและต่ำสุด
ลองพิจารณาภาพนี้

ฮิสโตแกรมของภาพนี้แสดงอยู่ด้านล่าง
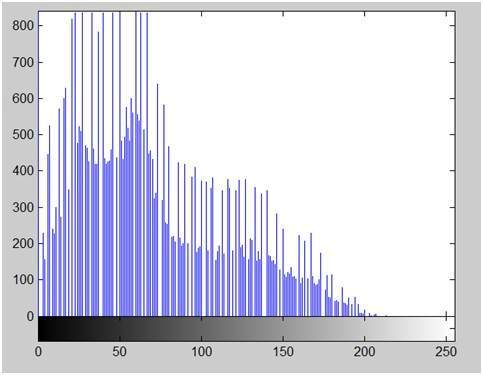
ตอนนี้เราคำนวณความคมชัดจากภาพนี้
ความคมชัด = 225
ตอนนี้เราจะเพิ่มความคมชัดของภาพ
การเพิ่มความคมชัดของภาพ:
สูตรสำหรับการยืดฮิสโตแกรมของภาพเพื่อเพิ่มความคมชัดคือ
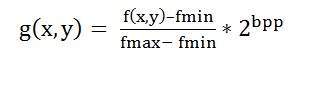
สูตรต้องการค้นหาความเข้มพิกเซลต่ำสุดและสูงสุดคูณด้วยระดับสีเทา ในกรณีของเราภาพคือ 8bpp ดังนั้นระดับสีเทาคือ 256
ค่าต่ำสุดคือ 0 และค่าสูงสุดคือ 225 ดังนั้นสูตรในกรณีของเราคือ
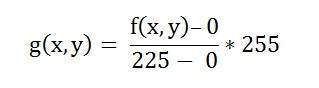
โดยที่ f (x, y) หมายถึงค่าของความเข้มของแต่ละพิกเซล สำหรับแต่ละ f (x, y) ในรูปภาพเราจะคำนวณสูตรนี้
หลังจากทำเช่นนี้เราจะสามารถเพิ่มความเปรียบต่างได้
ภาพต่อไปนี้ปรากฏขึ้นหลังจากใช้การยืดฮิสโตแกรม

ฮิสโตแกรมที่ยืดออกของภาพนี้แสดงไว้ด้านล่าง
สังเกตรูปร่างและสมมาตรของฮิสโตแกรม ขณะนี้ฮิสโตแกรมถูกยืดออกหรือขยายด้วยวิธีอื่น ลองดูสิ
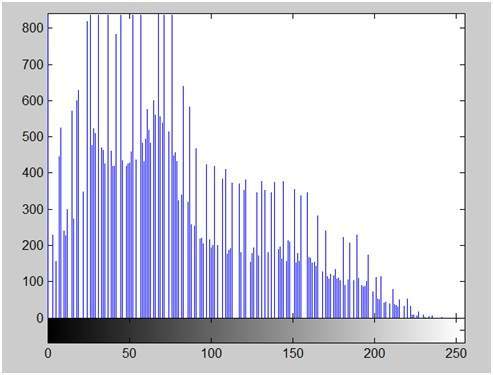
ในกรณีนี้สามารถคำนวณความคมชัดของภาพได้
ความคมชัด = 240
ดังนั้นเราสามารถพูดได้ว่าคอนทราสต์ของภาพเพิ่มขึ้น
หมายเหตุ: วิธีการเพิ่มความเปรียบต่างนี้ใช้ไม่ได้เสมอไป แต่ก็ล้มเหลวในบางกรณี
การยืดฮิสโตแกรมล้มเหลว
ดังที่เราได้กล่าวไปแล้วว่าอัลกอริทึมล้มเหลวในบางกรณี กรณีเหล่านี้รวมถึงรูปภาพด้วยเมื่อมีความเข้มของพิกเซล 0 และ 255 อยู่ในภาพ
เนื่องจากเมื่อความเข้มของพิกเซล 0 และ 255 ปรากฏในภาพดังนั้นในกรณีนี้จะกลายเป็นความเข้มของพิกเซลต่ำสุดและสูงสุดซึ่งจะทำลายสูตรเช่นนี้
สูตรดั้งเดิม
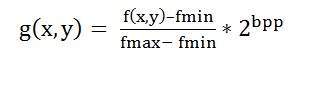
การใส่ค่ากรณีล้มเหลวในสูตร:
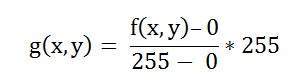
ทำให้นิพจน์นั้นง่ายขึ้น
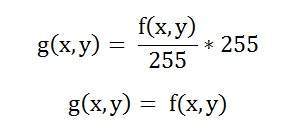
นั่นหมายความว่าภาพที่ส่งออกจะเท่ากับภาพที่ประมวลผล นั่นหมายความว่าไม่มีผลของการยืดฮิสโตแกรมในภาพนี้
PMF และ CDF ทั้งสองคำเป็นของความน่าจะเป็นและสถิติ ตอนนี้คำถามที่ควรเกิดขึ้นในใจของคุณนั่นคือเหตุใดเราจึงศึกษาความน่าจะเป็น เป็นเพราะแนวคิดทั้งสองนี้ของ PMF และ CDF จะถูกนำไปใช้ในบทช่วยสอนถัดไปของการทำให้เท่าเทียมกันของฮิสโตแกรม ดังนั้นหากคุณไม่รู้วิธีคำนวณ PMF และ CDF คุณจะไม่สามารถใช้การปรับสมดุลฮิสโตแกรมกับภาพของคุณได้
PMF คืออะไร?
PMF ย่อมาจากฟังก์ชันมวลความน่าจะเป็น ตามชื่อที่แนะนำจะให้ความน่าจะเป็นของตัวเลขแต่ละตัวในชุดข้อมูลหรือคุณสามารถพูดได้ว่าโดยทั่วไปจะให้จำนวนหรือความถี่ของแต่ละองค์ประกอบ
วิธีคำนวณ PMF:
เราจะคำนวณ PMF จากสองวิธีที่แตกต่างกัน อันดับแรกจากเมทริกซ์เพราะในบทช่วยสอนถัดไปเราต้องคำนวณ PMF จากเมทริกซ์และรูปภาพก็ไม่มีอะไรมากจากเมทริกซ์สองมิติ
จากนั้นเราจะใช้อีกตัวอย่างหนึ่งซึ่งเราจะคำนวณ PMF จากฮิสโตแกรม
พิจารณาเมทริกซ์นี้
| 1 | 2 | 7 | 5 | 6 |
| 7 | 2 | 3 | 4 | 5 |
| 0 | 1 | 5 | 7 | 3 |
| 1 | 2 | 5 | 6 | 7 |
| 6 | 1 | 0 | 3 | 4 |
ทีนี้ถ้าเราจะคำนวณ PMF ของเมทริกซ์นี้เราจะทำอย่างไร
ในตอนแรกเราจะรับค่าแรกในเมทริกซ์จากนั้นเราจะนับเวลาที่ค่านี้ปรากฏในเมทริกซ์ทั้งหมด หลังจากนับแล้วพวกเขาสามารถแสดงในฮิสโตแกรมหรือในตารางเช่นนี้ด้านล่าง
PMF
| 0 | 2 | 2/25 |
| 1 | 4 | 4/25 |
| 2 | 3 | 25/3 |
| 3 | 3 | 25/3 |
| 4 | 2 | 2/25 |
| 5 | 4 | 4/25 |
| 6 | 3 | 25/3 |
| 7 | 4 | 4/25 |
โปรดทราบว่าผลรวมของการนับต้องเท่ากับจำนวนค่าทั้งหมด
การคำนวณ PMF จากฮิสโตแกรม
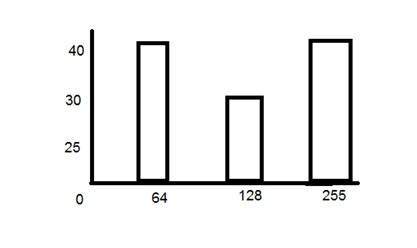
ฮิสโตแกรมด้านบนแสดงความถี่ของค่าระดับสีเทาสำหรับภาพ 8 บิตต่อพิกเซล
ตอนนี้ถ้าเราต้องคำนวณ PMF เราจะดูการนับของแต่ละแท่งจากแกนแนวตั้งแล้วหารด้วยจำนวนทั้งหมด
PMF ของฮิสโตแกรมข้างบนคือนี่
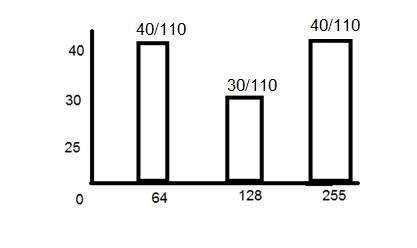
สิ่งสำคัญอีกอย่างที่ควรทราบในฮิสโตแกรมข้างต้นคือการไม่เพิ่มขึ้นอย่างจำเจ ดังนั้นเพื่อเพิ่มความซ้ำซากจำเจเราจะคำนวณ CDF
CDF คืออะไร?
CDF ย่อมาจากฟังก์ชันการกระจายสะสม เป็นฟังก์ชันที่คำนวณผลรวมสะสมของค่าทั้งหมดที่คำนวณโดย PMF โดยทั่วไปแล้วผลรวมก่อนหน้านี้
คำนวณอย่างไร?
เราจะคำนวณ CDF โดยใช้ฮิสโตแกรม นี่คือวิธีการทำ พิจารณาฮิสโตแกรมที่แสดงด้านบนซึ่งแสดง PMF
เนื่องจากฮิสโตแกรมนี้ไม่ได้เพิ่มขึ้นอย่างซ้ำซากจำเจดังนั้นจะทำให้มันเติบโตอย่างจำเจ
เราจะคงค่าแรกไว้เหมือนเดิมจากนั้นในค่าที่ 2 เราจะเพิ่มค่าแรกไปเรื่อย ๆ
นี่คือ CDF ของฟังก์ชัน PMF ด้านบน
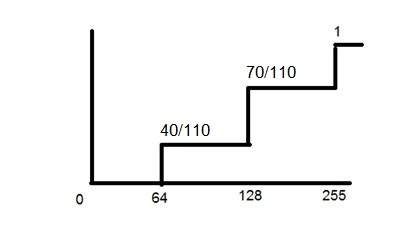
ตอนนี้ดังที่คุณเห็นจากกราฟด้านบนว่าค่าแรกของ PMF ยังคงเป็นอยู่ ค่าที่สองของ PMF จะถูกเพิ่มในค่าแรกและวางไว้เหนือ 128 ค่าที่สามของ PMF ถูกเพิ่มในค่าที่สองของ CDF ซึ่งให้ 110/110 ซึ่งเท่ากับ 1
และตอนนี้ฟังก์ชั่นนี้กำลังเติบโตอย่างจำเจซึ่งเป็นเงื่อนไขที่จำเป็นสำหรับการปรับสมดุลของฮิสโตแกรม
การใช้ PMF และ CDF ในการปรับสมดุลของฮิสโตแกรม
ฮิสโตแกรมอีควอไลเซอร์
การทำให้เท่าเทียมกันของฮิสโตแกรมจะกล่าวถึงในบทช่วยสอนถัดไป แต่จะมีการแนะนำสั้น ๆ เกี่ยวกับการทำให้เท่ากันของฮิสโตแกรมด้านล่าง
ฮิสโตแกรมอีควอไลเซอร์ใช้เพื่อเพิ่มความคมชัดของภาพ
PMF และ CDF ใช้ในการทำให้เท่าเทียมกันของฮิสโตแกรมตามที่อธิบายไว้ในตอนต้นของบทช่วยสอนนี้ ในการปรับสมดุลของฮิสโตแกรมขั้นตอนแรกและขั้นที่สองคือ PMF และ CDF เนื่องจากในฮิสโตแกรมอีควอไลเซอร์เราต้องทำให้ค่าพิกเซลทั้งหมดของรูปภาพเท่ากัน PMF จึงช่วยให้เราคำนวณความน่าจะเป็นของค่าพิกเซลแต่ละภาพในภาพ และ CDF ให้ผลรวมสะสมของค่าเหล่านี้แก่เรา ยิ่งไปกว่านั้น CDF นี้จะถูกคูณด้วยระดับเพื่อค้นหาความเข้มของพิกเซลใหม่ซึ่งจับคู่กับค่าเก่าและฮิสโตแกรมของคุณจะถูกทำให้เท่ากัน
เราได้เห็นแล้วว่าสามารถเพิ่มความเปรียบต่างได้โดยใช้การยืดฮิสโตแกรม ในบทช่วยสอนนี้เราจะมาดูกันว่าสามารถใช้การปรับสมดุลของฮิสโตแกรมเพื่อเพิ่มความเปรียบต่างได้อย่างไร
ก่อนที่จะทำการอีควอไลเซอร์ฮิสโตแกรมคุณต้องรู้แนวคิดสำคัญสองประการที่ใช้ในการปรับสมดุลฮิสโตแกรม แนวคิดทั้งสองนี้เรียกว่า PMF และ CDF
พวกเขาจะกล่าวถึงในบทแนะนำ PMF และ CDF ของเรา โปรดไปที่พวกเขาเพื่อทำความเข้าใจแนวคิดของการปรับสมดุลของฮิสโตแกรมให้สำเร็จ
ฮิสโตแกรม Equalization:
ฮิสโตแกรมอีควอไลเซอร์ใช้เพื่อเพิ่มความเปรียบต่าง ไม่จำเป็นว่าคอนทราสต์จะเพิ่มขึ้นเสมอไป อาจมีบางกรณีที่การทำให้เท่าเทียมกันของฮิสโตแกรมอาจแย่ลง ในกรณีนี้ความคมชัดจะลดลง
เริ่มต้นการปรับสมดุลของฮิสโตแกรมโดยใช้ภาพด้านล่างนี้เป็นภาพธรรมดา
ภาพ

ฮิสโตแกรมของภาพนี้:
ฮิสโตแกรมของภาพนี้แสดงไว้ด้านล่าง
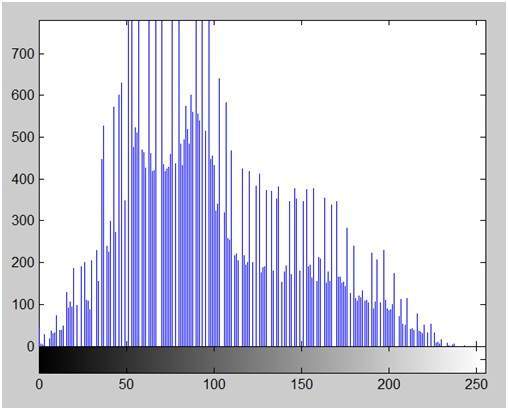
ตอนนี้เราจะทำการปรับค่าฮิสโตแกรมให้เท่ากัน
PMF:
ก่อนอื่นเราต้องคำนวณ PMF (ฟังก์ชันมวลความน่าจะเป็น) ของพิกเซลทั้งหมดในภาพนี้ หากคุณไม่ทราบวิธีคำนวณ PMF โปรดไปที่บทแนะนำการคำนวณ PMF ของเรา
CDF:
ขั้นตอนต่อไปของเราเกี่ยวข้องกับการคำนวณ CDF (ฟังก์ชันการกระจายสะสม) อีกครั้งหากคุณไม่รู้วิธีคำนวณ CDF โปรดไปที่บทช่วยสอนการคำนวณ CDF ของเรา
คำนวณ CDF ตามระดับสีเทา
ตัวอย่างเช่นให้พิจารณาสิ่งนี้ว่า CDF ที่คำนวณในขั้นตอนที่สองมีลักษณะเช่นนี้
| ค่าระดับสีเทา | ซีดีเอฟ |
|---|---|
| 0 | 0.11 |
| 1 | 0.22 |
| 2 | 0.55 |
| 3 | 0.66 |
| 4 | 0.77 |
| 5 | 0.88 |
| 6 | 0.99 |
| 7 | 1 |
จากนั้นในขั้นตอนนี้คุณจะคูณค่า CDF ด้วย (ระดับสีเทา (ลบ) 1)
พิจารณาว่าเรามีภาพ 3 bpp จากนั้นจำนวนเลเวลที่เรามีคือ 8 และ 1 ลบ 8 ได้ 7 เราก็คูณ CDF ด้วย 7 นี่คือสิ่งที่เราได้หลังจากการคูณ
| ค่าระดับสีเทา | ซีดีเอฟ | CDF * (ระดับ -1) |
|---|---|---|
| 0 | 0.11 | 0 |
| 1 | 0.22 | 1 |
| 2 | 0.55 | 3 |
| 3 | 0.66 | 4 |
| 4 | 0.77 | 5 |
| 5 | 0.88 | 6 |
| 6 | 0.99 | 6 |
| 7 | 1 | 7 |
ตอนนี้เรามีขั้นตอนสุดท้ายซึ่งเราต้องแมปค่าระดับสีเทาใหม่เป็นจำนวนพิกเซล
สมมติว่าค่าระดับสีเทาเก่าของเรามีจำนวนพิกเซลเหล่านี้
| ค่าระดับสีเทา | ความถี่ |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 10 |
| 5 | 12 |
| 6 | 14 |
| 7 | 16 |
ทีนี้ถ้าเราจับคู่ค่าใหม่ของเรากับนี่คือสิ่งที่เราได้
| ค่าระดับสีเทา | ค่าระดับสีเทาใหม่ | ความถี่ |
|---|---|---|
| 0 | 0 | 2 |
| 1 | 1 | 4 |
| 2 | 3 | 6 |
| 3 | 4 | 8 |
| 4 | 5 | 10 |
| 5 | 6 | 12 |
| 6 | 6 | 14 |
| 7 | 7 | 16 |
ตอนนี้จับคู่ค่าใหม่ที่คุณอยู่ในฮิสโตแกรมและคุณทำเสร็จแล้ว
ให้ใช้เทคนิคนี้กับภาพต้นฉบับของเรา หลังจากใช้แล้วเราได้ภาพต่อไปนี้และฮิสโตแกรมต่อไปนี้
ภาพการปรับสมดุลของฮิสโตแกรม

ฟังก์ชันการกระจายแบบสะสมของรูปภาพนี้
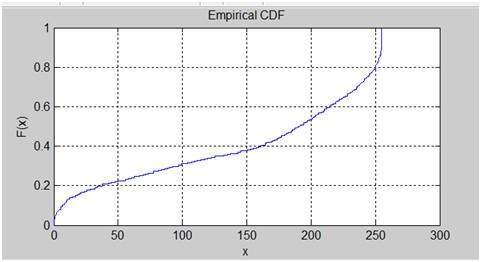
ฮิสโตแกรมการปรับสมดุล Histogram
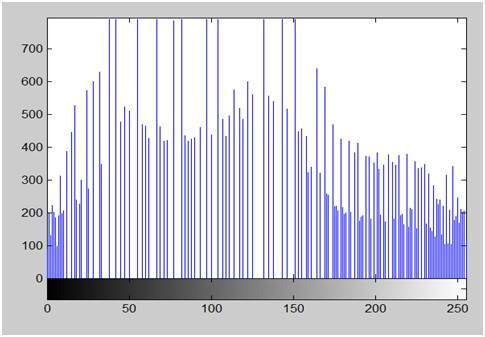
เปรียบเทียบทั้งฮิสโทแกรมและรูปภาพ

สรุป
ดังที่คุณเห็นได้อย่างชัดเจนจากภาพว่าความคมชัดของภาพใหม่ได้รับการปรับปรุงและฮิสโตแกรมได้รับการปรับให้เท่ากันด้วย นอกจากนี้ยังมีสิ่งสำคัญอีกประการหนึ่งที่ควรทราบในระหว่างการปรับสมดุลของฮิสโตแกรมรูปร่างโดยรวมของฮิสโตแกรมจะเปลี่ยนไปโดยที่ในฮิสโตแกรมยืดรูปร่างโดยรวมของฮิสโตแกรมจะยังคงเหมือนเดิม
เราได้พูดถึงการเปลี่ยนแปลงพื้นฐานบางประการในบทช่วยสอนเรื่องการแปลงขั้นพื้นฐาน ในบทช่วยสอนนี้เราจะดูการเปลี่ยนแปลงระดับสีเทาขั้นพื้นฐาน
การปรับปรุงภาพ
การปรับแต่งภาพให้คอนทราสต์ที่ดีขึ้นและภาพที่มีรายละเอียดมากขึ้นเมื่อเปรียบเทียบกับภาพที่ไม่ได้ปรับปรุง การปรับแต่งภาพมีแอพพลิเคชั่นมาก ใช้เพื่อปรับปรุงภาพทางการแพทย์ภาพที่ถ่ายด้วยการรับรู้ระยะไกลภาพจากดาวเทียม ฯลฯ
ฟังก์ชั่นการแปลงร่างได้รับด้านล่าง
s = T (r)
โดยที่ r คือพิกเซลของภาพอินพุตและ s คือพิกเซลของภาพที่ส่งออก T คือฟังก์ชันการแปลงที่จับคู่ค่าของ r แต่ละค่ากับค่า s การปรับปรุงภาพสามารถทำได้โดยการแปลงระดับสีเทาซึ่งจะกล่าวถึงด้านล่าง
การเปลี่ยนแปลงระดับสีเทา
การแปลงระดับสีเทาพื้นฐานมีสามแบบ
Linear
Logarithmic
อำนาจกฎหมาย
กราฟโดยรวมของการเปลี่ยนเหล่านี้แสดงไว้ด้านล่าง
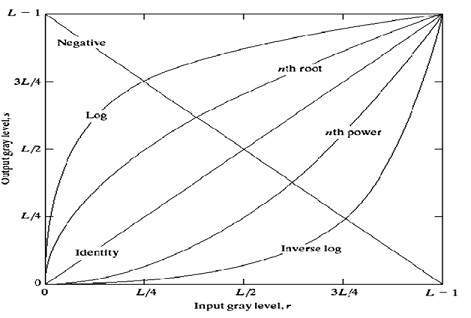
การแปลงเชิงเส้น
อันดับแรกเราจะดูการแปลงเชิงเส้น การแปลงเชิงเส้นรวมถึงเอกลักษณ์ที่เรียบง่ายและการเปลี่ยนแปลงเชิงลบ มีการพูดถึงการเปลี่ยนแปลงตัวตนในบทช่วยสอนเรื่องการแปลงภาพ แต่มีคำอธิบายสั้น ๆ เกี่ยวกับการเปลี่ยนแปลงนี้ที่นี่
การเปลี่ยนแปลงข้อมูลประจำตัวแสดงเป็นเส้นตรง ในการเปลี่ยนแปลงนี้ค่าแต่ละค่าของภาพอินพุตจะถูกจับคู่โดยตรงกับค่าอื่น ๆ ของภาพที่ส่งออก ส่งผลให้ภาพอินพุตและภาพเอาต์พุตเดียวกัน และด้วยเหตุนี้จึงเรียกว่าการเปลี่ยนแปลงตัวตน ได้แสดงไว้ด้านล่าง
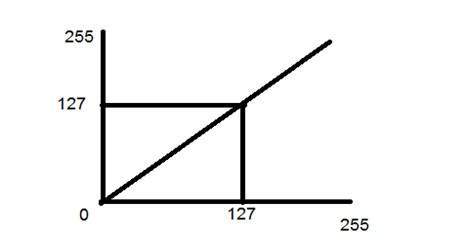
การเปลี่ยนแปลงเชิงลบ
การแปลงเชิงเส้นครั้งที่สองคือการแปลงเชิงลบซึ่งตรงกันข้ามกับการแปลงตัวตน ในการแปลงค่าลบแต่ละค่าของอิมเมจอินพุตจะถูกลบออกจาก L-1 และแมปลงบนรูปภาพเอาต์พุต
ผลเป็นแบบนี้บ้าง
อินพุตรูปภาพ

ภาพที่ส่งออก

ในกรณีนี้ได้ทำการเปลี่ยนแปลงต่อไปนี้แล้ว
s = (L - 1) - r
เนื่องจากภาพอินพุตของ Einstein เป็นภาพ 8 bpp ดังนั้นจำนวนระดับในภาพนี้จึงเป็น 256 เมื่อใส่ 256 ในสมการเราจะได้สิ่งนี้
s = 255 - ร
ดังนั้นแต่ละค่าจะถูกลบด้วย 255 และภาพผลลัพธ์ได้แสดงไว้ด้านบน สิ่งที่เกิดขึ้นก็คือพิกเซลที่สว่างขึ้นจะมืดลงและภาพที่มืดลงจะกลายเป็นแสง และส่งผลให้ภาพลักษณ์เป็นลบ
ได้แสดงไว้ในกราฟด้านล่าง
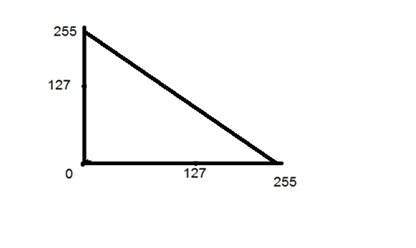
การแปลงลอการิทึม:
การแปลงลอการิทึมยังมีการแปลงอีกสองประเภท การแปลงบันทึกและการแปลงบันทึกผกผัน
บันทึกการเปลี่ยนแปลง
การแปลงบันทึกสามารถกำหนดได้โดยสูตรนี้
s = c บันทึก (r + 1)
โดยที่ s และ r คือค่าพิกเซลของเอาต์พุตและภาพอินพุตและ c เป็นค่าคงที่ ค่า 1 จะถูกเพิ่มให้กับค่าพิกเซลของภาพที่ป้อนเนื่องจากหากมีความเข้มของพิกเซลเป็น 0 ในภาพบันทึก (0) จะเท่ากับอินฟินิตี้ ดังนั้นจึงเพิ่ม 1 เพื่อให้ค่าต่ำสุดเป็นอย่างน้อย 1
ในระหว่างการแปลงบันทึกพิกเซลมืดในภาพจะขยายเมื่อเทียบกับค่าพิกเซลที่สูงขึ้น ค่าพิกเซลที่สูงขึ้นเป็นชนิดของการบีบอัดในการแปลงบันทึก ส่งผลให้เกิดการปรับปรุงภาพตามมา
ค่าของ c ในการแปลงบันทึกจะปรับประเภทของการเพิ่มประสิทธิภาพที่คุณกำลังมองหา
อินพุตรูปภาพ

บันทึก Tranform Image

การแปลงบันทึกผกผันตรงข้ามกับการแปลงบันทึก
อำนาจ - การเปลี่ยนแปลงกฎหมาย
ยังมีการเปลี่ยนแปลงอีกสองอย่างคือการแปลงกฎอำนาจซึ่งรวมถึงพลังที่ n และการแปลงรากที่ n การเปลี่ยนแปลงเหล่านี้สามารถกำหนดได้จากนิพจน์:
s = cr ^ γ
สัญลักษณ์γนี้เรียกว่าแกมมาเนื่องจากการเปลี่ยนแปลงนี้เรียกอีกอย่างว่าการแปลงแกมมา
การเปลี่ยนแปลงค่าของγจะแตกต่างกันไปตามการปรับปรุงของภาพ อุปกรณ์ / จอภาพที่แตกต่างกันมีการแก้ไขแกมมาของตัวเองนั่นคือสาเหตุที่ทำให้แสดงภาพด้วยความเข้มที่ต่างกัน
การแปลงประเภทนี้ใช้สำหรับการปรับปรุงภาพสำหรับอุปกรณ์แสดงผลประเภทต่างๆ แกมมาของอุปกรณ์แสดงผลต่างกัน ตัวอย่างเช่นแกมมาของ CRT อยู่ระหว่าง 1.8 ถึง 2.5 นั่นหมายความว่าภาพที่แสดงบน CRT นั้นมืด
การแก้ไขแกมมา
s = cr ^ γ
s = cr ^ (1 / 2.5)
ภาพเดียวกัน แต่มีค่าแกมมาต่างกันได้แสดงไว้ที่นี่
ตัวอย่างเช่น:
แกมมา = 10

แกมมา = 8

แกมมา = 6

บทช่วยสอนนี้เป็นแนวคิดเกี่ยวกับสัญญาณและระบบที่สำคัญอย่างหนึ่ง เราจะหารือเกี่ยวกับการสนทนาอย่างสมบูรณ์ มันคืออะไร? เป็นเพราะอะไร? เราจะบรรลุอะไรได้บ้าง?
เราจะเริ่มพูดคุยเกี่ยวกับการแปลงจากพื้นฐานของการประมวลผลภาพ
การประมวลผลภาพคืออะไร
ดังที่เราได้กล่าวไปแล้วในบทแนะนำเกี่ยวกับการประมวลผลภาพและในสัญญาณและระบบว่าการประมวลผลภาพเป็นการศึกษาสัญญาณและระบบไม่มากก็น้อยเพราะภาพไม่ได้เป็นเพียงสัญญาณสองมิติ
นอกจากนี้เรายังได้พูดคุยกันว่าในการประมวลผลภาพเรากำลังพัฒนาระบบที่มีอินพุตเป็นรูปภาพและเอาต์พุตจะเป็นรูปภาพ นี่แสดงเป็นภาพเป็น
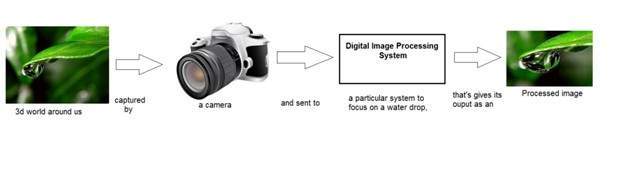
กล่องที่แสดงในรูปด้านบนที่ระบุว่า“ ระบบประมวลผลภาพดิจิทัล” อาจคิดว่าเป็นกล่องดำ
สามารถแสดงเป็น:

จนถึงตอนนี้เราไปถึงไหนแล้ว
จนถึงตอนนี้เราได้พูดถึงวิธีการสำคัญสองวิธีในการปรับแต่งภาพ หรืออีกนัยหนึ่งเราสามารถพูดได้ว่ากล่องดำของเราทำงานได้สองวิธีที่แตกต่างกันจนถึงตอนนี้
สองวิธีในการจัดการภาพที่แตกต่างกันคือ
Graphs (Histograms)

วิธีนี้เรียกว่าการประมวลผลฮิสโตแกรม เราได้พูดถึงรายละเอียดในบทช่วยสอนก่อนหน้านี้สำหรับการเพิ่มความคมชัดการปรับปรุงภาพความสว่าง ฯลฯ
Transformation functions
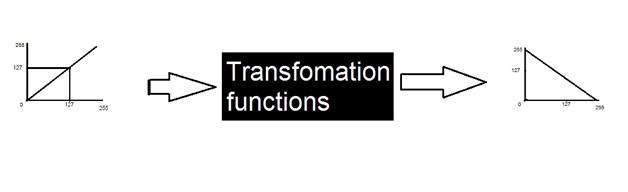
วิธีนี้เรียกว่าการแปลงร่างซึ่งเราได้พูดถึงการเปลี่ยนแปลงประเภทต่างๆและการแปลงระดับสีเทา
อีกวิธีหนึ่งในการจัดการกับภาพ
เราจะพูดถึงวิธีการจัดการกับรูปภาพอีกวิธีหนึ่ง วิธีอื่นนี้เรียกว่าการแปลง โดยปกติกล่องดำ (ระบบ) ที่ใช้สำหรับการประมวลผลภาพคือระบบ LTI หรือระบบไม่แปรผันของเวลาเชิงเส้น ตามเส้นตรงเราหมายถึงระบบที่เอาต์พุตเป็นเส้นตรงเสมอไม่บันทึกหรือเลขชี้กำลังหรืออื่น ๆ และตามเวลาที่ไม่แปรเปลี่ยนเราหมายถึงระบบที่ยังคงเหมือนเดิมในช่วงเวลา
ตอนนี้เราจะใช้วิธีที่สามนี้ สามารถแสดงเป็น

สามารถแสดงทางคณิตศาสตร์ได้สองวิธี
g(x,y) = h(x,y) * f(x,y)
สามารถอธิบายได้ว่า "มาสก์เชื่อมต่อกับรูปภาพ"
หรือ
g(x,y) = f(x,y) * h(x,y)
สามารถอธิบายได้ว่าเป็น "ภาพที่เชื่อมต่อด้วยหน้ากาก"
มีสองวิธีในการแสดงสิ่งนี้เนื่องจากตัวดำเนินการ Convolution (*) เป็นแบบสับเปลี่ยน h (x, y) คือหน้ากากหรือตัวกรอง
มาส์กคืออะไร?
หน้ากากยังเป็นสัญญาณ สามารถแสดงด้วยเมทริกซ์สองมิติ โดยปกติมาสก์จะมีขนาด 1x1, 3x3, 5x5, 7x7 หน้ากากควรเป็นเลขคี่เสมอเพราะคนอื่นฉลาดคุณจะหาจุดกึ่งกลางของหน้ากากไม่เจอ ทำไมเราต้องหาตรงกลางของหน้ากาก คำตอบอยู่ด้านล่างในหัวข้อวิธีดำเนินการ Convolution?
วิธีการทำ Convolution?
ในการดำเนินการ Convolution กับรูปภาพควรทำตามขั้นตอนต่อไปนี้
พลิกหน้ากาก (แนวนอนและแนวตั้ง) เพียงครั้งเดียว
เลื่อนหน้ากากไปที่รูปภาพ
คูณองค์ประกอบที่เกี่ยวข้องแล้วเพิ่ม
ทำซ้ำขั้นตอนนี้จนกว่าค่าทั้งหมดของภาพจะได้รับการคำนวณ
ตัวอย่าง Convolution
มาทำการสนทนากัน ขั้นตอนที่ 1 คือการพลิกหน้ากาก
หน้ากาก:
มาสก์ของเรากันเถอะ
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
พลิกหน้ากากในแนวนอน
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
พลิกหน้ากากในแนวตั้ง
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
ภาพ:
ลองพิจารณาภาพให้เป็นแบบนี้
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
การแปลง
การแปลงมาสก์เหนือรูปภาพ มันทำด้วยวิธีนี้ วางกึ่งกลางของมาสก์ที่แต่ละองค์ประกอบของรูปภาพ คูณองค์ประกอบที่เกี่ยวข้องแล้วเพิ่มและวางผลลัพธ์ลงในองค์ประกอบของภาพที่คุณวางตรงกลางมาสก์
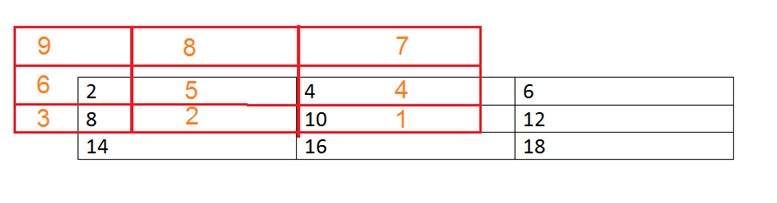
กล่องสีแดงคือมาสก์และค่าในสีส้มคือค่าของมาสก์ กล่องสีดำและค่าเป็นของรูปภาพ ตอนนี้สำหรับพิกเซลแรกของภาพค่าจะถูกคำนวณเป็น
พิกเซลแรก = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)
= 10 + 16 + 16 + 10
= 52
วาง 52 ในภาพต้นฉบับที่ดัชนีแรกและทำซ้ำขั้นตอนนี้สำหรับแต่ละพิกเซลของภาพ
ทำไมต้อง Convolution
Convolution สามารถบรรลุบางสิ่งบางอย่างซึ่งสองวิธีก่อนหน้านี้ในการจัดการภาพไม่สามารถบรรลุได้ ซึ่งรวมถึงการเบลอการเหลาการตรวจจับขอบการลดจุดรบกวน ฯลฯ
หน้ากากคืออะไร.
หน้ากากคือตัวกรอง แนวคิดของการกำบังเรียกอีกอย่างว่าการกรองเชิงพื้นที่ Masking เรียกอีกอย่างว่าการกรอง ในแนวคิดนี้เราจัดการกับการกรองที่ดำเนินการโดยตรงกับรูปภาพ
ตัวอย่างมาสก์ได้แสดงไว้ด้านล่าง
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
การกรองคืออะไร
ขั้นตอนการกรองเรียกอีกอย่างหนึ่งว่าการสร้างมาสก์ด้วยรูปภาพ เนื่องจากกระบวนการนี้เหมือนกันกับคอนโวลูชั่นดังนั้นหน้ากากกรองจึงเรียกอีกอย่างว่าหน้ากากคอนโวลูชั่น
วิธีการทำ
กระบวนการทั่วไปของการกรองและการใช้มาสก์ประกอบด้วยการย้ายมาสก์ตัวกรองจากจุดหนึ่งไปยังอีกจุดหนึ่งในรูปภาพ ในแต่ละจุด (x, y) ของภาพต้นฉบับการตอบสนองของตัวกรองจะคำนวณโดยความสัมพันธ์ที่กำหนดไว้ล่วงหน้า ค่าตัวกรองทั้งหมดถูกกำหนดไว้ล่วงหน้าและเป็นมาตรฐาน
ประเภทของตัวกรอง
โดยทั่วไปมีตัวกรองสองประเภท หนึ่งเรียกว่าเป็นตัวกรองเชิงเส้นหรือตัวกรองการปรับให้เรียบและอื่น ๆ เรียกว่าตัวกรองโดเมนความถี่
ทำไมต้องใช้ตัวกรอง
ใช้ฟิลเตอร์กับภาพเพื่อวัตถุประสงค์หลายประการ การใช้งานทั่วไปสองอย่างมีดังต่อไปนี้:
ฟิลเตอร์ใช้สำหรับการเบลอภาพและการลดสัญญาณรบกวน
มีการใช้ฟิลเตอร์หรือการตรวจจับขอบและความคม
การลดความเบลอและสัญญาณรบกวน:
ฟิลเตอร์มักใช้สำหรับการเบลอและลดจุดรบกวน การเบลอภาพใช้ในขั้นตอนก่อนการประมวลผลเช่นการลบรายละเอียดขนาดเล็กออกจากภาพก่อนการแยกวัตถุขนาดใหญ่
มาสก์สำหรับการเบลอ
มาสก์ทั่วไปสำหรับการเบลอคือ
ตัวกรองกล่อง
ตัวกรองถัวเฉลี่ยถ่วงน้ำหนัก
ในกระบวนการเบลอเราจะลดเนื้อหาขอบในภาพและพยายามทำให้การเปลี่ยนระหว่างความเข้มของพิกเซลที่แตกต่างกันราบรื่นที่สุด
นอกจากนี้ยังสามารถลดจุดรบกวนได้โดยใช้การเบลอ
การตรวจจับขอบและความคมชัด:
นอกจากนี้ยังสามารถใช้มาสก์หรือฟิลเตอร์สำหรับการตรวจจับขอบในภาพและเพื่อเพิ่มความคมชัดของภาพ
ขอบคืออะไร
นอกจากนี้เรายังสามารถพูดได้ว่าการเปลี่ยนแปลงอย่างกะทันหันของความไม่ต่อเนื่องในภาพเรียกว่าขอบ การเปลี่ยนภาพที่มีนัยสำคัญเรียกว่าเป็นขอบภาพที่มีขอบแสดงอยู่ด้านล่าง
ภาพต้นฉบับ

ภาพเดียวกันกับขอบ

มีการพูดถึงการแนะนำสั้น ๆ เกี่ยวกับการเบลอในแบบฝึกหัดก่อนหน้านี้เกี่ยวกับแนวคิดเรื่องมาสก์ แต่เราจะพูดถึงอย่างเป็นทางการที่นี่
เบลอ
ในการเบลอเราเบลอภาพง่ายๆ ภาพจะดูคมชัดหรือมีรายละเอียดมากขึ้นหากเราสามารถรับรู้วัตถุและรูปร่างทั้งหมดในนั้นได้อย่างถูกต้อง ตัวอย่างเช่น. ภาพที่มีใบหน้าดูชัดเจนเมื่อเราสามารถระบุตาหูจมูกริมฝีปากหน้าผาก ฯลฯ ได้ชัดเจนมาก รูปร่างของวัตถุนี้เกิดจากขอบของมัน ดังนั้นในการเบลอเราจึงลดเนื้อหาขอบและทำให้การเปลี่ยนจากสีหนึ่งไปเป็นอีกสีหนึ่งได้อย่างราบรื่น
การเบลอเทียบกับการซูม
คุณอาจเห็นภาพเบลอเมื่อคุณซูมภาพ เมื่อคุณซูมภาพโดยใช้การจำลองแบบพิกเซลและปัจจัยการซูมเพิ่มขึ้นคุณจะเห็นภาพเบลอ ภาพนี้มีรายละเอียดน้อยเช่นกัน แต่ไม่ใช่การเบลอที่แท้จริง
เนื่องจากในการซูมคุณจะเพิ่มพิกเซลใหม่ให้กับภาพซึ่งจะเพิ่มจำนวนพิกเซลโดยรวมในภาพในขณะที่การเบลอจำนวนพิกเซลของภาพปกติและภาพเบลอยังคงเท่าเดิม
ตัวอย่างทั่วไปของภาพเบลอ

ประเภทของตัวกรอง
การเบลอภาพสามารถทำได้หลายวิธี ประเภทของฟิลเตอร์ทั่วไปที่ใช้ในการเบลอคือ
ค่าเฉลี่ยตัวกรอง
ตัวกรองถัวเฉลี่ยถ่วงน้ำหนัก
ตัวกรอง Gaussian
จากสามข้อนี้เราจะพูดถึงสองข้อแรกที่นี่และ Gaussian จะกล่าวถึงในบทช่วยสอนที่กำลังจะมาถึงในภายหลัง
ค่าเฉลี่ยตัวกรอง
ตัวกรองค่าเฉลี่ยเรียกอีกอย่างว่าตัวกรองกล่องและตัวกรองค่าเฉลี่ย ตัวกรองค่าเฉลี่ยมีคุณสมบัติดังต่อไปนี้
ต้องเป็นเลขคี่
ผลรวมขององค์ประกอบทั้งหมดควรเป็น 1
องค์ประกอบทั้งหมดควรเหมือนกัน
ถ้าเราทำตามกฎนี้สำหรับมาสก์ 3x3 เราได้ผลลัพธ์ดังต่อไปนี้
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
เนื่องจากเป็นมาสก์ 3x3 จึงหมายความว่ามี 9 เซลล์ เงื่อนไขที่ว่าผลรวมขององค์ประกอบทั้งหมดควรเท่ากับ 1 สามารถทำได้โดยหารแต่ละค่าด้วย 9 As
1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 = 9/9 = 1
ผลลัพธ์ของมาสก์ 3x3 บนรูปภาพแสดงอยู่ด้านล่าง
ภาพต้นฉบับ:

ภาพเบลอ

อาจจะเห็นผลไม่ชัดเจนสักเท่าไหร่ มาเพิ่มความเบลอกันเถอะ สามารถเพิ่มความเบลอได้โดยการเพิ่มขนาดของมาสก์ ยิ่งเป็นขนาดของหน้ากากมากเท่าไหร่ก็ยิ่งมีความเบลอมากเท่านั้น เนื่องจากมีมาสก์ที่มากขึ้นจะมีการรองรับจำนวนพิกเซลมากขึ้นและมีการกำหนดการเปลี่ยนแปลงที่ราบรื่นเพียงครั้งเดียว
ผลลัพธ์ของมาสก์ 5x5 บนรูปภาพแสดงอยู่ด้านล่าง
ภาพต้นฉบับ:

ภาพเบลอ:

ในทำนองเดียวกันถ้าเราเพิ่มมาสก์การเบลอจะมากขึ้นและผลลัพธ์จะแสดงด้านล่าง
ผลลัพธ์ของมาสก์ขนาด 7x7 บนรูปภาพแสดงอยู่ด้านล่าง
ภาพต้นฉบับ:

ภาพเบลอ:

ผลลัพธ์ของมาสก์ขนาด 9x9 บนรูปภาพแสดงอยู่ด้านล่าง
ภาพต้นฉบับ:

ภาพเบลอ:

ผลลัพธ์ของมาสก์ขนาด 11x11 บนรูปภาพแสดงอยู่ด้านล่าง
ภาพต้นฉบับ:

ภาพเบลอ:

ตัวกรองถัวเฉลี่ยถ่วงน้ำหนัก
ในตัวกรองค่าเฉลี่ยถ่วงน้ำหนักเราให้น้ำหนักกับค่ากลางมากขึ้น เนื่องจากการมีส่วนร่วมของศูนย์กลายเป็นค่าที่เหลือมากขึ้น เนื่องจากการกรองแบบถัวเฉลี่ยถ่วงน้ำหนักเราสามารถควบคุมการเบลอได้จริง
คุณสมบัติของตัวกรองถัวเฉลี่ยถ่วงน้ำหนักคือ
ต้องเป็นเลขคี่
ผลรวมขององค์ประกอบทั้งหมดควรเป็น 1
น้ำหนักขององค์ประกอบกลางควรมากกว่าองค์ประกอบอื่น ๆ ทั้งหมด
ตัวกรอง 1
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 1 | 1 |
คุณสมบัติทั้งสองมีความพึงพอใจซึ่ง ได้แก่ (1 และ 3) แต่ทรัพย์สิน 2 ไม่พอใจ. ดังนั้นเพื่อให้เป็นที่พอใจเราจะหารตัวกรองทั้งหมดด้วย 10 อย่างง่าย ๆ หรือคูณด้วย 1/10
ตัวกรอง 2
| 1 | 1 | 1 |
| 1 | 10 | 1 |
| 1 | 1 | 1 |
ปัจจัยหาร = 18.
เราได้พูดคุยสั้น ๆ เกี่ยวกับการตรวจจับขอบในบทแนะนำเบื้องต้นเกี่ยวกับมาสก์ เราจะพูดถึงการตรวจจับขอบอย่างเป็นทางการที่นี่
ขอบคืออะไร
นอกจากนี้เรายังสามารถพูดได้ว่าการเปลี่ยนแปลงอย่างกะทันหันของความไม่ต่อเนื่องในภาพเรียกว่าขอบ การเปลี่ยนภาพที่มีนัยสำคัญเรียกว่าเป็นขอบ
ประเภทของขอบ
ขอบโดยทั่วไปมีสามประเภท:
ขอบแนวนอน
ขอบแนวตั้ง
ขอบในแนวทแยง
ทำไมต้องตรวจจับขอบ
ข้อมูลรูปร่างส่วนใหญ่ของรูปภาพอยู่ในขอบ ก่อนอื่นเราจะตรวจจับขอบเหล่านี้ในภาพและโดยใช้ฟิลเตอร์เหล่านี้จากนั้นโดยการปรับปรุงพื้นที่ของภาพที่มีขอบความคมของภาพจะเพิ่มขึ้นและภาพจะชัดเจนขึ้น
ต่อไปนี้เป็นมาสก์สำหรับการตรวจจับขอบที่เราจะพูดถึงในบทช่วยสอนที่กำลังจะมาถึง
ปรีวิทย์โอเปอเรเตอร์
ผู้ดำเนินการ Sobel
หน้ากากโรบินสันเข็มทิศ
หน้ากาก Krisch Compass
Laplacian Operator.
ตัวกรองทั้งหมดที่กล่าวมาข้างต้นคือฟิลเตอร์เชิงเส้นหรือฟิลเตอร์ปรับให้เรียบ
ปรีวิทย์โอเปอเรเตอร์
ตัวดำเนินการ Prewitt ใช้สำหรับตรวจจับขอบในแนวนอนและแนวตั้ง
ผู้ดำเนินการ Sobel
ตัวดำเนินการ sobel นั้นคล้ายกับตัวดำเนินการ Prewitt มาก นอกจากนี้ยังเป็นมาสก์ลอกเลียนแบบและใช้สำหรับการตรวจจับขอบ นอกจากนี้ยังคำนวณขอบทั้งในแนวนอนและแนวตั้ง
หน้ากากโรบินสันเข็มทิศ
ตัวดำเนินการนี้เรียกอีกอย่างว่าหน้ากากทิศทาง ในตัวดำเนินการนี้เราใช้หน้ากากเดียวและหมุนไปตามทิศทางหลักของเข็มทิศทั้ง 8 ทิศทางเพื่อคำนวณขอบของแต่ละทิศทาง
มาสก์ Kirsch Compass
Kirsch Compass Mask ยังเป็นมาสก์อนุพันธ์ที่ใช้สำหรับค้นหาขอบ หน้ากาก Kirsch ยังใช้สำหรับการคำนวณขอบในทุกทิศทาง
Laplacian Operator.
Laplacian Operator ยังเป็นตัวดำเนินการอนุพันธ์ที่ใช้ในการหาขอบในภาพ Laplacian เป็นมาสก์อนุพันธ์อันดับสอง สามารถแบ่งออกได้อีกเป็น laplacian positive และ negative laplacian
หน้ากากทั้งหมดนี้พบขอบ บางตัวพบในแนวนอนและแนวตั้งบางตัวพบในทิศทางเดียวเท่านั้นและบางตัวพบในทุกทิศทาง แนวคิดต่อไปที่เกิดขึ้นหลังจากนี้คือการทำให้คมชัดซึ่งสามารถทำได้เมื่อดึงขอบออกจากภาพแล้ว
เหลา:
การเหลาจะตรงข้ามกับการเบลอ ในการเบลอเราลดเนื้อหาขอบและในความคมเราเพิ่มเนื้อหาขอบ ดังนั้นในการเพิ่มเนื้อหาขอบในภาพเราต้องหาขอบก่อน
สามารถค้นหาขอบได้ด้วยวิธีใดวิธีหนึ่งที่อธิบายไว้ข้างต้นโดยใช้ตัวดำเนินการใด ๆ หลังจากหาขอบแล้วเราจะเพิ่มขอบเหล่านั้นลงในภาพดังนั้นภาพจะมีขอบมากขึ้นและมันจะดูคมขึ้น
นี่เป็นวิธีหนึ่งในการทำให้ภาพคมชัดขึ้น
ภาพที่คมชัดแสดงอยู่ด้านล่าง
ภาพต้นฉบับ

เพิ่มความคมชัดของภาพ

ตัวดำเนินการ Prewitt ใช้สำหรับการตรวจจับขอบในภาพ ตรวจจับขอบสองประเภท:
ขอบแนวนอน
ขอบแนวตั้ง
ขอบคำนวณโดยใช้ความแตกต่างระหว่างความเข้มของพิกเซลที่สอดคล้องกันของรูปภาพ มาสก์ทั้งหมดที่ใช้สำหรับการตรวจจับขอบเรียกอีกอย่างว่ามาสก์อนุพันธ์ เนื่องจากตามที่เราได้ระบุไว้หลายครั้งก่อนหน้านี้ในบทเรียนชุดนี้รูปภาพก็เป็นสัญญาณเช่นกันดังนั้นการเปลี่ยนแปลงสัญญาณจึงสามารถคำนวณได้โดยใช้ความแตกต่างเท่านั้น นั่นคือสาเหตุที่ตัวดำเนินการเหล่านี้เรียกอีกอย่างว่าตัวดำเนินการอนุพันธ์หรือมาสก์อนุพันธ์
มาสก์อนุพันธ์ทั้งหมดควรมีคุณสมบัติดังต่อไปนี้:
ควรมีเครื่องหมายตรงข้ามอยู่ในหน้ากาก
ผลรวมของมาสก์ควรเท่ากับศูนย์
น้ำหนักที่มากขึ้นหมายถึงการตรวจจับขอบที่มากขึ้น
ตัวดำเนินการ Prewitt มีหน้ากากสองอันสำหรับตรวจจับขอบในแนวนอนและอีกอันสำหรับตรวจจับขอบในแนวตั้ง
ทิศทางแนวตั้ง:
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
หน้ากากด้านบนจะพบขอบในแนวตั้งและเป็นเพราะคอลัมน์ศูนย์ในแนวตั้ง เมื่อคุณปรับมาสก์นี้กับรูปภาพมันจะทำให้คุณได้ขอบแนวตั้งในรูปภาพ
มันทำงานอย่างไร:
เมื่อเราใช้มาสก์นี้กับรูปภาพจะมีขอบแนวตั้งที่เด่นชัด มันทำงานเหมือนเป็นอนุพันธ์ลำดับแรกและคำนวณความแตกต่างของความเข้มของพิกเซลในพื้นที่ขอบ เนื่องจากคอลัมน์กลางเป็นศูนย์จึงไม่รวมค่าดั้งเดิมของรูปภาพ แต่จะคำนวณความแตกต่างของค่าพิกเซลด้านขวาและด้านซ้ายรอบขอบนั้น สิ่งนี้จะเพิ่มความเข้มของขอบและเพิ่มขึ้นเมื่อเทียบกับภาพต้นฉบับ
ทิศทางแนวนอน:
| -1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
หน้ากากด้านบนจะพบขอบในแนวนอนและเป็นเพราะคอลัมน์ศูนย์นั้นอยู่ในแนวนอน เมื่อคุณจะปรับมาสก์นี้เข้ากับรูปภาพมันจะมีขอบแนวนอนที่เด่นชัดในภาพ
มันทำงานอย่างไร:
มาสก์นี้จะทำให้ขอบแนวนอนเด่นชัดในรูปภาพ นอกจากนี้ยังทำงานบนหลักการของมาสก์ด้านบนและคำนวณความแตกต่างระหว่างความเข้มของพิกเซลของขอบเฉพาะ เนื่องจากแถวกลางของมาสก์ประกอบด้วยเลขศูนย์จึงไม่รวมค่าดั้งเดิมของขอบในภาพ แต่จะคำนวณความแตกต่างของความเข้มพิกเซลด้านบนและด้านล่างของขอบเฉพาะ จึงเพิ่มการเปลี่ยนแปลงอย่างฉับพลันของความรุนแรงและทำให้มองเห็นขอบได้ชัดเจนขึ้น ทั้งสองหน้ากากข้างต้นเป็นไปตามหลักการของมาสก์อนุพันธ์ ทั้งสองมาสก์มีเครื่องหมายตรงข้ามกันและทั้งสองมาสก์ผลรวมเท่ากับศูนย์ เงื่อนไขที่สามจะใช้ไม่ได้กับโอเปอเรเตอร์นี้เนื่องจากทั้งสองมาสก์ข้างต้นเป็นแบบมาตรฐานและเราไม่สามารถเปลี่ยนค่าในตัวดำเนินการนี้ได้
ตอนนี้ได้เวลาดูการใช้งานมาสก์เหล่านี้แล้ว:
ภาพตัวอย่าง:
ต่อไปนี้เป็นภาพตัวอย่างที่เราจะใช้สองหน้ากากข้างบนพร้อมกัน

หลังจากใช้ Vertical Mask:
หลังจากใช้มาสก์แนวตั้งกับภาพตัวอย่างด้านบนแล้วจะได้ภาพต่อไปนี้ ภาพนี้มีขอบแนวตั้ง คุณสามารถตัดสินได้อย่างถูกต้องมากขึ้นโดยเปรียบเทียบกับภาพขอบแนวนอน

หลังจากใช้ Horizontal Mask:
หลังจากใช้มาสก์แนวนอนกับภาพตัวอย่างด้านบนแล้วจะได้ภาพต่อไปนี้

เปรียบเทียบ:
ดังที่คุณเห็นว่าในภาพแรกที่เราใช้มาสก์แนวตั้งขอบแนวตั้งทั้งหมดจะมองเห็นได้ชัดเจนกว่าภาพต้นฉบับ ในภาพที่สองเราได้ใช้มาสก์แนวนอนและทำให้มองเห็นขอบแนวนอนทั้งหมด ด้วยวิธีนี้คุณจะเห็นว่าเราสามารถตรวจจับขอบทั้งแนวนอนและแนวตั้งจากรูปภาพได้
ตัวดำเนินการ sobel นั้นคล้ายกับตัวดำเนินการ Prewitt มาก นอกจากนี้ยังเป็นมาสก์ลอกเลียนแบบและใช้สำหรับการตรวจจับขอบ เช่นเดียวกับตัวดำเนินการ sobel ตัวดำเนินการ Prewitt ยังใช้เพื่อตรวจจับขอบสองประเภทในภาพ:
ทิศทางแนวตั้ง
ทิศทางแนวนอน
ความแตกต่างกับ Prewitt Operator:
ความแตกต่างที่สำคัญคือในตัวดำเนินการ sobel ค่าสัมประสิทธิ์ของมาสก์จะไม่คงที่และสามารถปรับเปลี่ยนได้ตามความต้องการของเราเว้นแต่จะไม่ละเมิดคุณสมบัติใด ๆ ของมาสก์อนุพันธ์
ต่อไปนี้เป็น Mask แนวตั้งของ Sobel Operator:
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
มาสก์นี้ทำงานเหมือนกับมาสก์แนวตั้งของตัวดำเนินการ Prewitt ทุกประการ มีความแตกต่างเพียงอย่างเดียวนั่นคือมีค่า "2" และ "-2" อยู่ตรงกลางของคอลัมน์ที่หนึ่งและสาม เมื่อนำไปใช้กับรูปภาพมาสก์นี้จะเน้นที่ขอบแนวตั้ง
มันทำงานอย่างไร:
เมื่อเราใช้มาสก์นี้กับรูปภาพจะมีขอบแนวตั้งที่เด่นชัด มันทำงานเหมือนเป็นอนุพันธ์ลำดับแรกและคำนวณความแตกต่างของความเข้มของพิกเซลในพื้นที่ขอบ
เนื่องจากคอลัมน์กลางเป็นศูนย์จึงไม่รวมค่าดั้งเดิมของรูปภาพ แต่จะคำนวณความแตกต่างของค่าพิกเซลด้านขวาและด้านซ้ายรอบขอบนั้น นอกจากนี้ค่ากลางของทั้งคอลัมน์แรกและคอลัมน์ที่สามคือ 2 และ -2 ตามลำดับ
สิ่งนี้ให้น้ำหนักกับค่าพิกเซลรอบขอบมากขึ้น สิ่งนี้จะเพิ่มความเข้มของขอบและเพิ่มขึ้นเมื่อเทียบกับภาพต้นฉบับ
ต่อไปนี้คือ Mask แนวนอนของ Sobel Operator:
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
หน้ากากด้านบนจะพบขอบในแนวนอนและเป็นเพราะคอลัมน์ศูนย์นั้นอยู่ในแนวนอน เมื่อคุณจะปรับมาสก์นี้เข้ากับรูปภาพมันจะมีขอบแนวนอนที่เด่นชัดในภาพ ข้อแตกต่างเพียงอย่างเดียวคือมี 2 และ -2 เป็นองค์ประกอบกึ่งกลางของแถวแรกและแถวที่สาม
มันทำงานอย่างไร:
มาสก์นี้จะทำให้ขอบแนวนอนเด่นชัดในรูปภาพ นอกจากนี้ยังทำงานบนหลักการของมาสก์ด้านบนและคำนวณความแตกต่างระหว่างความเข้มของพิกเซลของขอบเฉพาะ เนื่องจากแถวกลางของมาสก์ประกอบด้วยเลขศูนย์จึงไม่รวมค่าดั้งเดิมของขอบในภาพ แต่จะคำนวณความแตกต่างของความเข้มพิกเซลด้านบนและด้านล่างของขอบเฉพาะ จึงเพิ่มการเปลี่ยนแปลงอย่างฉับพลันของความรุนแรงและทำให้มองเห็นขอบได้ชัดเจนขึ้น
ตอนนี้ได้เวลาดูการใช้งานมาสก์เหล่านี้แล้ว:
ภาพตัวอย่าง:
ต่อไปนี้เป็นภาพตัวอย่างที่เราจะใช้สองหน้ากากข้างบนพร้อมกัน

หลังจากใช้ Vertical Mask:
หลังจากใช้มาสก์แนวตั้งกับภาพตัวอย่างด้านบนแล้วจะได้ภาพต่อไปนี้

หลังจากใช้ Horizontal Mask:
หลังจากใช้มาสก์แนวนอนกับภาพตัวอย่างด้านบนแล้วจะได้ภาพต่อไปนี้

เปรียบเทียบ:
ดังที่คุณเห็นว่าในภาพแรกที่เราใช้มาสก์แนวตั้งขอบแนวตั้งทั้งหมดจะมองเห็นได้ชัดเจนกว่าภาพต้นฉบับ ในภาพที่สองเราได้ใช้มาสก์แนวนอนและทำให้มองเห็นขอบแนวนอนทั้งหมด
ด้วยวิธีนี้คุณจะเห็นว่าเราสามารถตรวจจับขอบทั้งแนวนอนและแนวตั้งจากรูปภาพได้ นอกจากนี้หากคุณเปรียบเทียบผลลัพธ์ของตัวดำเนินการ sobel กับตัวดำเนินการ Prewitt คุณจะพบว่าตัวดำเนินการ sobel พบขอบมากขึ้นหรือทำให้ขอบมองเห็นได้ชัดเจนขึ้นเมื่อเทียบกับ Prewitt Operator
เนื่องจากในตัวดำเนินการ sobel เราได้จัดสรรน้ำหนักให้กับความเข้มของพิกเซลรอบ ๆ ขอบมากขึ้น
ใช้น้ำหนักมากขึ้นในการมาส์ก
ตอนนี้เรายังสามารถเห็นได้ว่าถ้าเราใช้น้ำหนักมากขึ้นกับมาสก์ก็จะยิ่งได้ขอบมากขึ้นสำหรับเรา ตามที่กล่าวไว้ในตอนต้นของบทช่วยสอนว่าไม่มีสัมประสิทธิ์คงที่ในตัวดำเนินการ sobel ดังนั้นนี่คือตัวดำเนินการแบบถ่วงน้ำหนักอื่น
| -1 | 0 | 1 |
| -5 | 0 | 5 |
| -1 | 0 | 1 |
หากคุณสามารถเปรียบเทียบผลลัพธ์ของมาสก์นี้กับมาสก์แนวตั้งของ Prewitt เป็นที่ชัดเจนว่ามาสก์นี้จะให้ขอบมากกว่าเมื่อเทียบกับ Prewitt เพียงเพราะเรามีน้ำหนักมากกว่าในหน้ากาก
หน้ากากโรบินสันเป็นอีกประเภทหนึ่งของมาสก์ Derrivate ซึ่งใช้สำหรับการตรวจจับขอบ ตัวดำเนินการนี้เรียกอีกอย่างว่าหน้ากากทิศทาง ในโอเปอเรเตอร์นี้เราใช้หน้ากากเดียวและหมุนไปตามทิศทางหลักของเข็มทิศทั้ง 8 ทิศทางดังต่อไปนี้:
North
ตะวันตกเฉียงเหนือ
West
ตะวันตกเฉียงใต้
South
ตะวันออกเฉียงใต้
East
ภาคตะวันออกเฉียงเหนือ
ไม่มีหน้ากากที่ตายตัว คุณสามารถใช้หน้ากากใดก็ได้และคุณต้องหมุนเพื่อหาขอบตามทิศทางที่กล่าวมาทั้งหมด มาสก์ทั้งหมดจะถูกหมุนบนฐานของทิศทางของคอลัมน์ศูนย์
ตัวอย่างเช่นลองดูหน้ากากต่อไปนี้ซึ่งอยู่ในทิศทางเหนือแล้วหมุนเพื่อสร้างมาสก์ทิศทางทั้งหมด
หน้ากากทิศเหนือ
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
หน้ากากทิศตะวันตกเฉียงเหนือ
| 0 | 1 | 2 |
| -1 | 0 | 1 |
| -2 | -1 | 0 |
หน้ากากทิศตะวันตก
| 1 | 2 | 1 |
| 0 | 0 | 0 |
| -1 | -2 | -1 |
หน้ากากทิศตะวันตกเฉียงใต้
| 2 | 1 | 0 |
| 1 | 0 | -1 |
| 0 | -1 | -2 |
หน้ากากทิศใต้
| 1 | 0 | -1 |
| 2 | 0 | -2 |
| 1 | 0 | -1 |
หน้ากากทิศตะวันออกเฉียงใต้
| 0 | -1 | -2 |
| 1 | 0 | -1 |
| 2 | 1 | 0 |
หน้ากากทิศตะวันออก
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
หน้ากากทิศตะวันออกเฉียงเหนือ
| -2 | -1 | 0 |
| -1 | 0 | 1 |
| 0 | 1 | 2 |
ดังที่คุณจะเห็นว่าทิศทางทั้งหมดถูกครอบคลุมบนพื้นฐานของทิศทางศูนย์ แต่ละหน้ากากจะให้ขอบตามทิศทางของมัน ตอนนี้เรามาดูผลลัพธ์ของมาสก์ด้านบนทั้งหมด สมมติว่าเรามีภาพตัวอย่างซึ่งเราต้องหาขอบทั้งหมด นี่คือภาพตัวอย่างของเรา:
ภาพตัวอย่าง:

ตอนนี้เราจะใช้ตัวกรองด้านบนทั้งหมดกับภาพนี้และเราจะได้ผลลัพธ์ต่อไปนี้
ขอบทิศเหนือ

ขอบทิศตะวันตกเฉียงเหนือ

ขอบทิศทางตะวันตก

ขอบทิศตะวันตกเฉียงใต้

ขอบทิศใต้

ขอบทิศตะวันออกเฉียงใต้

ขอบทิศทางตะวันออก

ขอบทิศตะวันออกเฉียงเหนือ

อย่างที่คุณเห็นว่าด้วยการใช้มาสก์ข้างต้นทั้งหมดคุณจะได้รับขอบในทุกทิศทาง ผลลัพธ์ยังขึ้นอยู่กับภาพ สมมติว่ามีรูปภาพซึ่งไม่มีขอบทิศทางตะวันออกเฉียงเหนือดังนั้นหน้ากากนั้นจะใช้ไม่ได้ผล
Kirsch Compass Mask ยังเป็นมาสก์อนุพันธ์ที่ใช้สำหรับค้นหาขอบ นี่ก็เหมือนกับเข็มทิศโรบินสันค้นหาขอบในทั้งแปดทิศทางของเข็มทิศ ความแตกต่างเพียงอย่างเดียวระหว่างหน้ากาก Robinson และ kirsch compass คือใน Kirsch เรามีหน้ากากมาตรฐาน แต่ใน Kirsch เราเปลี่ยนหน้ากากตามความต้องการของเราเอง
ด้วยความช่วยเหลือของ Kirsch Compass Masks เราสามารถค้นหาขอบได้ในแปดทิศทางต่อไปนี้
North
ตะวันตกเฉียงเหนือ
West
ตะวันตกเฉียงใต้
South
ตะวันออกเฉียงใต้
East
ภาคตะวันออกเฉียงเหนือ
เราใช้มาสก์มาตรฐานซึ่งเป็นไปตามคุณสมบัติทั้งหมดของมาสก์อนุพันธ์จากนั้นหมุนเพื่อหาขอบ
ตัวอย่างเช่นลองดูหน้ากากต่อไปนี้ซึ่งอยู่ในทิศทางเหนือแล้วหมุนเพื่อสร้างมาสก์ทิศทางทั้งหมด
หน้ากากทิศเหนือ
| -3 | -3 | 5 |
| -3 | 0 | 5 |
| -3 | -3 | 5 |
หน้ากากทิศตะวันตกเฉียงเหนือ
| -3 | 5 | 5 |
| -3 | 0 | 5 |
| -3 | -3 | -3 |
หน้ากากทิศตะวันตก
| 5 | 5 | 5 |
| -3 | 0 | -3 |
| -3 | -3 | -3 |
หน้ากากทิศตะวันตกเฉียงใต้
| 5 | 5 | -3 |
| 5 | 0 | -3 |
| -3 | -3 | -3 |
หน้ากากทิศใต้
| 5 | -3 | -3 |
| 5 | 0 | -3 |
| 5 | -3 | -3 |
หน้ากากทิศตะวันออกเฉียงใต้
| -3 | -3 | -3 |
| 5 | 0 | -3 |
| 5 | 5 | -3 |
หน้ากากทิศตะวันออก
| -3 | -3 | -3 |
| -3 | 0 | -3 |
| 5 | 5 | 5 |
หน้ากากทิศตะวันออกเฉียงเหนือ
| -3 | -3 | -3 |
| -3 | 0 | 5 |
| -3 | 5 | 5 |
อย่างที่คุณเห็นว่ามีการปิดทุกทิศทางและแต่ละหน้ากากจะให้ขอบทิศทางของตัวเอง ตอนนี้เพื่อช่วยให้คุณเข้าใจแนวคิดของมาสก์เหล่านี้ได้ดีขึ้นเราจะนำมาใช้กับภาพจริง สมมติว่าเรามีภาพตัวอย่างซึ่งเราต้องหาขอบทั้งหมด นี่คือภาพตัวอย่างของเรา:
ภาพตัวอย่าง

ตอนนี้เราจะใช้ตัวกรองด้านบนทั้งหมดกับภาพนี้และเราจะได้ผลลัพธ์ต่อไปนี้
ขอบทิศเหนือ

ขอบทิศตะวันตกเฉียงเหนือ

ขอบทิศทางตะวันตก

ขอบทิศตะวันตกเฉียงใต้

ขอบทิศใต้

ขอบทิศตะวันออกเฉียงใต้

ขอบทิศทางตะวันออก

ขอบทิศตะวันออกเฉียงเหนือ

อย่างที่คุณเห็นว่าด้วยการใช้มาสก์ข้างต้นทั้งหมดคุณจะได้รับขอบในทุกทิศทาง ผลลัพธ์ยังขึ้นอยู่กับภาพ สมมติว่ามีรูปภาพซึ่งไม่มีขอบทิศทางตะวันออกเฉียงเหนือดังนั้นหน้ากากนั้นจะใช้ไม่ได้ผล
Laplacian Operator ยังเป็นตัวดำเนินการอนุพันธ์ที่ใช้ในการหาขอบในภาพ ความแตกต่างที่สำคัญระหว่าง Laplacian กับตัวดำเนินการอื่น ๆ เช่น Prewitt, Sobel, Robinson และ Kirsch คือทั้งหมดนี้เป็นมาสก์อนุพันธ์ลำดับที่หนึ่ง แต่ Laplacian เป็นมาสก์อนุพันธ์ลำดับที่สอง ในมาสก์นี้เรามีการจำแนกประเภทเพิ่มเติมอีกสองประเภทหนึ่งคือตัวดำเนินการ Laplacian เชิงบวกและอื่น ๆ คือตัวดำเนินการ Laplacian เชิงลบ
ความแตกต่างอีกอย่างระหว่าง Laplacian และตัวดำเนินการอื่น ๆ คือไม่เหมือนกับตัวดำเนินการอื่น ๆ Laplacian ไม่ได้นำขอบออกไปในทิศทางใดทิศทางหนึ่ง แต่จะใช้ขอบในการจำแนกประเภทต่อไปนี้
ขอบขาเข้า
ขอบด้านนอก
มาดูกันว่าตัวดำเนินการ Laplacian ทำงานอย่างไร
ตัวดำเนินการ Laplacian ที่เป็นบวก:
ใน Positive Laplacian เรามีมาสก์มาตรฐานซึ่งองค์ประกอบตรงกลางของหน้ากากควรเป็นลบและองค์ประกอบมุมของหน้ากากควรเป็นศูนย์
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
ตัวดำเนินการ Laplacian ที่เป็นบวกใช้เพื่อดึงขอบออกด้านนอกของภาพ
ตัวดำเนินการ Laplacian เชิงลบ:
ในตัวดำเนินการ Laplacian ค่าลบเรายังมีมาสก์มาตรฐานซึ่งองค์ประกอบตรงกลางควรเป็นบวก องค์ประกอบทั้งหมดในมุมควรเป็นศูนย์และองค์ประกอบที่เหลือทั้งหมดในมาสก์ควรเป็น -1
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
ตัวดำเนินการ Laplacian เชิงลบใช้เพื่อดึงขอบเข้าด้านในของรูปภาพ
มันทำงานอย่างไร:
Laplacian เป็นตัวดำเนินการอนุพันธ์ ใช้ไฮไลต์ความไม่ต่อเนื่องของระดับสีเทาในภาพและพยายามพิจารณาขนาดพื้นที่ที่มีระดับสีเทาที่แตกต่างกันอย่างช้าๆ ผลลัพธ์ที่ได้จากการดำเนินการนี้จะสร้างภาพที่มีเส้นขอบสีเทาและความไม่ต่อเนื่องอื่น ๆ บนพื้นหลังสีเข้ม สิ่งนี้ทำให้เกิดขอบด้านในและด้านนอกของรูปภาพ
สิ่งสำคัญคือวิธีใช้ฟิลเตอร์เหล่านี้กับรูปภาพ จำไว้ว่าเราไม่สามารถใช้ตัวดำเนินการ Laplacian ทั้งบวกและลบกับรูปภาพเดียวกันได้ เราต้องใช้เพียงอันเดียว แต่สิ่งที่ต้องจำก็คือถ้าเราใช้ตัวดำเนินการ Laplacian ที่เป็นบวกกับภาพเราจะลบภาพผลลัพธ์ออกจากภาพต้นฉบับเพื่อให้ได้ภาพที่คมชัดขึ้น ในทำนองเดียวกันถ้าเราใช้ตัวดำเนินการ Laplacian ที่เป็นลบเราก็ต้องเพิ่มภาพผลลัพธ์ลงในภาพต้นฉบับเพื่อให้ได้ภาพที่คมชัดขึ้น
ลองใช้ฟิลเตอร์เหล่านี้กับรูปภาพและดูว่าจะทำให้เราเข้าและออกจากขอบภาพได้อย่างไร สมมติว่าเรามีภาพตัวอย่างดังต่อไปนี้
ภาพตัวอย่าง

After applying Positive Laplacian Operator:
หลังจากใช้ตัวดำเนินการ Laplacian ที่เป็นบวกเราจะได้ภาพต่อไปนี้

After applying Negative Laplacian Operator:
หลังจากใช้ตัวดำเนินการ Laplacian ลบเราจะได้ภาพต่อไปนี้

เราได้จัดการกับรูปภาพในหลายโดเมน ตอนนี้เรากำลังประมวลผลสัญญาณ (ภาพ) ในโดเมนความถี่ เนื่องจากอนุกรมฟูเรียร์และโดเมนความถี่นี้เป็นคณิตศาสตร์ล้วนๆดังนั้นเราจะพยายามย่อส่วนของคณิตศาสตร์นั้นให้น้อยที่สุดและมุ่งเน้นไปที่การใช้งานในกรมทรัพย์สินทางปัญญามากขึ้น
การวิเคราะห์โดเมนความถี่
จนถึงตอนนี้โดเมนทั้งหมดที่เราวิเคราะห์สัญญาณเราวิเคราะห์ตามเวลา แต่ในโดเมนความถี่เราไม่ได้วิเคราะห์สัญญาณเกี่ยวกับเวลา แต่เกี่ยวกับความถี่
ความแตกต่างระหว่างโดเมนเชิงพื้นที่และโดเมนความถี่
ในโดเมนเชิงพื้นที่เราจัดการกับรูปภาพตามที่เป็นจริง ค่าพิกเซลของภาพจะเปลี่ยนไปตามฉาก ในขณะที่โดเมนความถี่เราจัดการกับอัตราที่ค่าพิกเซลกำลังเปลี่ยนแปลงในโดเมนเชิงพื้นที่
เพื่อความเรียบง่ายลองใส่วิธีนี้
Spatial domain

ในโดเมนเชิงพื้นที่อย่างง่ายเราจัดการโดยตรงกับเมทริกซ์รูปภาพ ในขณะที่โดเมนความถี่เราจัดการภาพเช่นนี้
โดเมนความถี่
ก่อนอื่นเราเปลี่ยนรูปภาพเป็นการแจกแจงความถี่ จากนั้นระบบกล่องดำของเราจะทำการประมวลผลสิ่งที่ต้องดำเนินการและผลลัพธ์ของกล่องดำในกรณีนี้ไม่ใช่ภาพ แต่เป็นการแปลง หลังจากดำเนินการแปลงแบบผกผันแล้วจะถูกแปลงเป็นรูปภาพที่ดูในโดเมนเชิงพื้นที่
สามารถดูเป็นภาพได้
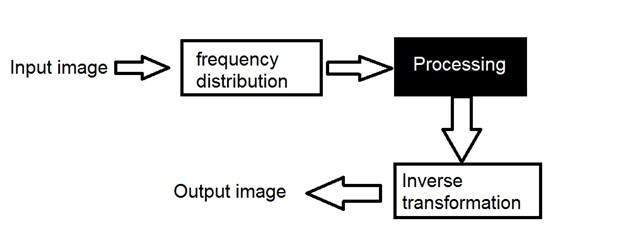
ที่นี่เราได้ใช้คำว่าการเปลี่ยนแปลง แท้จริงแล้วหมายถึงอะไร?
การเปลี่ยนแปลง
สัญญาณสามารถแปลงจากโดเมนเวลาเป็นโดเมนความถี่โดยใช้ตัวดำเนินการทางคณิตศาสตร์ที่เรียกว่าการแปลง มีการเปลี่ยนแปลงหลายอย่างที่ทำเช่นนี้ บางส่วนได้รับด้านล่าง
ซีรี่ส์ฟูเรียร์
การเปลี่ยนแปลงฟูเรียร์
ลาปลาซแปลงร่าง
Z แปลง
จากทั้งหมดนี้เราจะพูดถึงอนุกรมฟูริเยร์และการแปลงฟูเรียร์อย่างละเอียดในบทช่วยสอนครั้งต่อไป
ส่วนประกอบความถี่
รูปภาพใด ๆ ในโดเมนเชิงพื้นที่สามารถแสดงในโดเมนความถี่ได้ แต่จริงๆแล้วความถี่นี้หมายถึงอะไร
เราจะแบ่งส่วนประกอบความถี่ออกเป็นสองส่วนหลัก ๆ
High frequency components
ส่วนประกอบความถี่สูงสอดคล้องกับขอบในรูปภาพ
Low frequency components
ส่วนประกอบความถี่ต่ำในภาพสอดคล้องกับพื้นที่เรียบ
ในบทช่วยสอนล่าสุดของการวิเคราะห์โดเมนความถี่เราได้พูดคุยกันว่าอนุกรมฟูริเยร์และการแปลงฟูริเยร์ใช้เพื่อแปลงสัญญาณเป็นโดเมนความถี่
Fourier
ฟูริเยร์เป็นนักคณิตศาสตร์ในปี 1822 เขาให้อนุกรมฟูริเยร์และการแปลงฟูเรียร์เพื่อแปลงสัญญาณเป็นโดเมนความถี่
Fourier Series
อนุกรมฟูริเยร์ระบุว่าสัญญาณเป็นระยะสามารถแสดงเป็นผลรวมของไซน์และโคไซน์เมื่อคูณด้วยน้ำหนักที่แน่นอนนอกจากนี้ยังระบุว่าสัญญาณเป็นระยะสามารถแบ่งออกเป็นสัญญาณเพิ่มเติมได้ด้วยคุณสมบัติต่อไปนี้
สัญญาณคือไซน์และโคไซน์
สัญญาณเป็นฮาร์มอนิกของกันและกัน
สามารถดูเป็นภาพได้
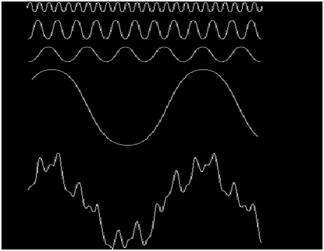
ในสัญญาณข้างต้นสัญญาณสุดท้ายคือผลรวมของสัญญาณทั้งหมดข้างต้น นี่คือความคิดของฟูเรียร์
คำนวณอย่างไร
เนื่องจากดังที่เราได้เห็นในโดเมนความถี่ในการประมวลผลภาพในโดเมนความถี่เราจำเป็นต้องแปลงภาพโดยใช้เป็นโดเมนความถี่ก่อนและเราต้องใช้เวลาผกผันของผลลัพธ์เพื่อแปลงกลับเป็นโดเมนเชิงพื้นที่ นั่นเป็นเหตุผลว่าทำไมอนุกรมฟูริเยร์และการแปลงฟูริเยร์จึงมีสองสูตร หนึ่งสำหรับการแปลงและอีกอันแปลงกลับเป็นโดเมนเชิงพื้นที่
อนุกรมฟูริเยร์
อนุกรมฟูริเยร์สามารถแสดงได้ด้วยสูตรนี้
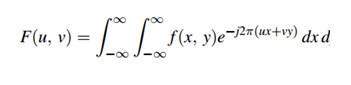
สูตรนี้สามารถคำนวณผกผันได้
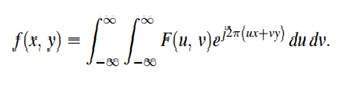
การแปลงฟูเรียร์
การแปลงฟูเรียร์ระบุเพียงว่าสัญญาณที่ไม่ใช่คาบที่มีพื้นที่ใต้เส้นโค้ง จำกัด สามารถแสดงเป็นอินทิกรัลของไซน์และโคไซน์หลังจากคูณด้วยน้ำหนักที่แน่นอน
การแปลงฟูริเยร์มีแอพพลิเคชั่นที่หลากหลายซึ่งรวมถึงการบีบอัดภาพ (เช่นการบีบอัด JPEG) การกรองและการวิเคราะห์ภาพ
ความแตกต่างระหว่างอนุกรมฟูริเยร์และการแปลง
แม้ว่าอนุกรมฟูริเยร์และการแปลงฟูริเยร์จะได้รับจากฟูริเยร์ แต่ความแตกต่างระหว่างอนุกรมฟูริเยร์นั้นใช้กับสัญญาณเป็นระยะและการแปลงฟูริเยร์จะใช้กับสัญญาณที่ไม่ใช่คาบ
ใช้อันไหนกับภาพ.
ตอนนี้คำถามคือว่าจะใช้อันไหนกับรูปภาพอนุกรมฟูริเยร์หรือการแปลงฟูริเยร์ คำตอบสำหรับคำถามนี้อยู่ที่ความจริงที่ว่าภาพคืออะไร รูปภาพไม่เป็นระยะ และเนื่องจากภาพไม่เป็นช่วงเวลาดังนั้นการแปลงฟูริเยร์จึงถูกใช้เพื่อแปลงเป็นโดเมนความถี่
การแปลงฟูเรียร์แบบไม่ต่อเนื่อง
เนื่องจากเรากำลังจัดการกับรูปภาพและภาพดิจิทัลที่ไม่ต่อเนื่องดังนั้นสำหรับภาพดิจิทัลเราจะดำเนินการเกี่ยวกับการแปลงฟูเรียร์แบบไม่ต่อเนื่อง

พิจารณาระยะฟูเรียร์ข้างต้นของไซน์ ประกอบด้วยสามสิ่ง
ความถี่เชิงพื้นที่
Magnitude
Phase
ความถี่เชิงพื้นที่เกี่ยวข้องโดยตรงกับความสว่างของภาพ ขนาดของไซนัสเกี่ยวข้องโดยตรงกับความเปรียบต่าง คอนทราสต์คือความแตกต่างระหว่างความเข้มพิกเซลสูงสุดและต่ำสุด เฟสมีข้อมูลสี
สูตรสำหรับการแปลงฟูเรียร์แบบไม่ต่อเนื่อง 2 มิติได้รับด้านล่าง
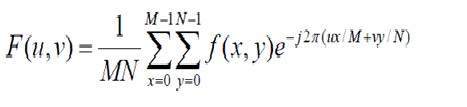
การแปลงฟูเรียร์แบบไม่ต่อเนื่องคือการแปลงฟูเรียร์ตัวอย่างดังนั้นจึงมีตัวอย่างบางส่วนที่แสดงถึงรูปภาพ ในสูตรด้านบน f (x, y) แสดงถึงรูปภาพและ F (u, v) หมายถึงการแปลงฟูเรียร์แบบไม่ต่อเนื่อง สูตรสำหรับการแปลงฟูเรียร์แบบไม่ต่อเนื่องผกผัน 2 มิติได้รับด้านล่าง
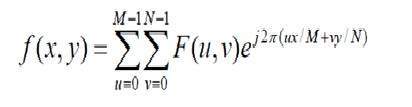
การแปลงฟูริเยร์แบบไม่ต่อเนื่องผกผันจะแปลงการแปลงฟูเรียร์กลับไปเป็นรูปภาพ
พิจารณาสัญญาณนี้
ตอนนี้เราจะเห็นภาพซึ่งเราจะคำนวณสเปกตรัมขนาด FFT จากนั้นเปลี่ยนขนาดสเปกตรัม FFT จากนั้นเราจะนำ Log ของสเปกตรัมที่เลื่อนนั้น
ภาพต้นฉบับ

ฟูริเยร์เปลี่ยนขนาดสเปกตรัม

การเปลี่ยนรูปแบบ Shifted Fourier

สเปกตรัมขนาดที่เปลี่ยนไป

ในบทช่วยสอนที่แล้วเราได้พูดถึงภาพในโดเมนความถี่ ในบทช่วยสอนนี้เราจะกำหนดความสัมพันธ์ระหว่างโดเมนความถี่และรูปภาพ (โดเมนเชิงพื้นที่)
ตัวอย่างเช่น:
ลองพิจารณาตัวอย่างนี้

รูปภาพเดียวกันในโดเมนความถี่สามารถแสดงเป็นไฟล์.

ตอนนี้ความสัมพันธ์ระหว่างอิมเมจหรือโดเมนเชิงพื้นที่และโดเมนความถี่คืออะไร ความสัมพันธ์นี้สามารถอธิบายได้ด้วยทฤษฎีบทซึ่งเรียกว่าทฤษฎีบท Convolution
ทฤษฎีบทการแปลง
ความสัมพันธ์ระหว่างโดเมนเชิงพื้นที่และโดเมนความถี่สามารถกำหนดได้โดยทฤษฎีบทคอนโวลูชั่น
ทฤษฎีบทการแปลงสามารถแสดงเป็น.
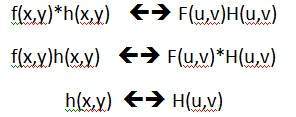
สามารถระบุได้ว่า Convolution ในโดเมนเชิงพื้นที่เท่ากับการกรองในโดเมนความถี่และในทางกลับกัน
การกรองในโดเมนความถี่สามารถแสดงได้ดังต่อไปนี้:

The steps in filtering are given below.
ในขั้นตอนแรกเราต้องทำการประมวลผลภาพล่วงหน้าในโดเมนเชิงพื้นที่หมายถึงเพิ่มคอนทราสต์หรือความสว่าง
จากนั้นเราจะทำการแปลงฟูเรียร์แบบไม่ต่อเนื่องของภาพ
จากนั้นเราจะจัดกึ่งกลางของการแปลงฟูริเยร์แบบไม่ต่อเนื่องเนื่องจากเราจะนำการแปลงฟูเรียร์ที่ไม่ต่อเนื่องมาอยู่ตรงกลางจากมุม
จากนั้นเราจะใช้การกรองหมายความว่าเราจะคูณการแปลงฟูเรียร์ด้วยฟังก์ชันตัวกรอง
จากนั้นเราจะเลื่อน DFT จากกึ่งกลางไปที่มุมอีกครั้ง
ขั้นตอนสุดท้ายจะใช้ในการแปลงฟูเรียร์แบบไม่ต่อเนื่องผกผันเพื่อนำผลลัพธ์กลับจากโดเมนความถี่เป็นโดเมนเชิงพื้นที่
และขั้นตอนของการประมวลผลหลังนี้เป็นทางเลือกเช่นเดียวกับการประมวลผลล่วงหน้าซึ่งเราเพียงแค่เพิ่มลักษณะของภาพ
ฟิลเตอร์
แนวคิดของตัวกรองในโดเมนความถี่เหมือนกับแนวคิดของหน้ากากในการแปลงสัญญาณ
หลังจากแปลงรูปภาพเป็นโดเมนความถี่แล้วตัวกรองบางตัวจะถูกนำไปใช้ในกระบวนการกรองเพื่อดำเนินการประมวลผลภาพประเภทต่างๆ การประมวลผลรวมถึงการเบลอภาพการทำให้ภาพคมชัดเป็นต้น
ประเภททั่วไปของตัวกรองสำหรับวัตถุประสงค์เหล่านี้ ได้แก่ :
ตัวกรองความถี่สูงในอุดมคติ
ตัวกรองความถี่ต่ำในอุดมคติ
Gaussian high pass filter
ตัวกรองความถี่ต่ำ Gaussian
ในบทช่วยสอนถัดไปเราจะพูดถึงรายละเอียดเกี่ยวกับตัวกรอง
ในบทช่วยสอนสุดท้ายเราจะพูดคุยสั้น ๆ เกี่ยวกับตัวกรอง ในบทช่วยสอนนี้เราจะพูดคุยเกี่ยวกับพวกเขาอย่างละเอียด ก่อนที่จะพูดคุยเกี่ยวกับมาสก์กันก่อน แนวคิดของหน้ากากได้รับการกล่าวถึงในบทช่วยสอนเรื่องการแปลงร่างและมาสก์
มาสก์เบลอเทียบกับมาสก์อนุพันธ์
เราจะทำการเปรียบเทียบระหว่างการเบลอมาสก์และมาสก์อนุพันธ์
มาสก์เบลอ:
มาสก์การเบลอมีคุณสมบัติดังต่อไปนี้
ค่าทั้งหมดในมาสก์การเบลอเป็นค่าบวก
ผลรวมของค่าทั้งหมดเท่ากับ 1
เนื้อหาขอบจะลดลงโดยใช้มาสก์การเบลอ
เมื่อขนาดของมาส์กโตขึ้นจะมีผลต่อความเรียบเนียนมากขึ้น
มาสก์อนุพันธ์:
มาสก์อนุพันธ์มีคุณสมบัติดังต่อไปนี้
มาสก์อนุพันธ์มีค่าบวกและค่าลบ
ผลรวมของค่าทั้งหมดในมาสก์อนุพันธ์เท่ากับศูนย์
เนื้อหาขอบจะเพิ่มขึ้นโดยมาสก์อนุพันธ์
เมื่อขนาดของมาสก์ใหญ่ขึ้นเนื้อหาขอบก็จะเพิ่มขึ้น
ความสัมพันธ์ระหว่างการเบลอมาสก์และมาสก์อนุพันธ์กับฟิลเตอร์ความถี่สูงและฟิลเตอร์ความถี่ต่ำ
ความสัมพันธ์ระหว่างมาสก์การเบลอและมาสก์อนุพันธ์ที่มีตัวกรองความถี่สูงและตัวกรองความถี่ต่ำสามารถกำหนดได้ง่ายๆว่า
มาสก์เบลอเรียกอีกอย่างว่าโลว์พาสฟิลเตอร์
มาสก์อนุพันธ์เรียกอีกอย่างว่าตัวกรองความถี่สูง
ส่วนประกอบความถี่สูงและส่วนประกอบความถี่ความถี่ต่ำ
ส่วนประกอบความถี่สูงหมายถึงขอบในขณะที่ส่วนประกอบความถี่ความถี่ต่ำหมายถึงบริเวณที่ราบเรียบ
ตัวกรองความถี่ต่ำและความถี่สูงในอุดมคติ
นี่คือตัวอย่างทั่วไปของตัวกรองความถี่ต่ำ
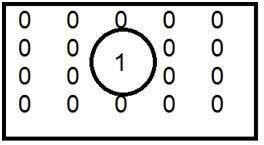
เมื่อวางไว้ด้านในและศูนย์วางไว้ด้านนอกเราจะได้ภาพเบลอ ตอนนี้เมื่อเราเพิ่มขนาด 1 ความเบลอก็จะเพิ่มขึ้นและเนื้อหาขอบจะลดลง
นี่คือตัวอย่างทั่วไปของตัวกรองความถี่สูง
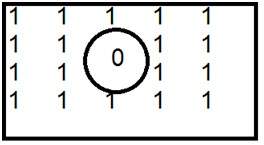
เมื่อใส่ 0 เข้าไปข้างในเราจะได้ขอบซึ่งทำให้เราได้ภาพร่าง ตัวกรองความถี่ต่ำที่ดีเยี่ยมในโดเมนความถี่ได้รับด้านล่าง

ตัวกรองความถี่ต่ำในอุดมคติสามารถแสดงเป็นกราฟิกได้
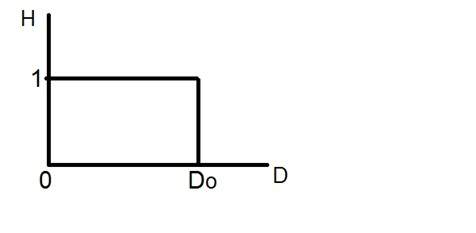
ทีนี้ลองใช้ฟิลเตอร์นี้กับภาพจริงแล้วมาดูกันว่าเราได้อะไร
ภาพตัวอย่าง.

รูปภาพในโดเมนความถี่

ใช้ฟิลเตอร์เหนือรูปภาพนี้

รูปภาพผลลัพธ์

ในทำนองเดียวกันตัวกรองความถี่สูงในอุดมคติสามารถใช้กับรูปภาพได้ แต่เห็นได้ชัดว่าผลลัพธ์จะแตกต่างกันเนื่องจากความถี่ต่ำจะลดเนื้อหาที่มีขอบและความถี่สูงจะเพิ่มขึ้น
Gaussian Low pass และ Gaussian High pass filter
Gaussian low pass และ Gaussian high pass filter ช่วยลดปัญหาที่เกิดขึ้นในตัวกรองความถี่ต่ำและความถี่สูงในอุดมคติ
ปัญหานี้เรียกว่าเอฟเฟกต์เสียงเรียกเข้า นี่เป็นเพราะเหตุผลเนื่องจากในบางจุดการเปลี่ยนระหว่างสีหนึ่งไปเป็นอีกสีไม่สามารถกำหนดได้อย่างแม่นยำเนื่องจากเอฟเฟกต์เสียงเรียกเข้าจะปรากฏที่จุดนั้น
ดูกราฟนี้
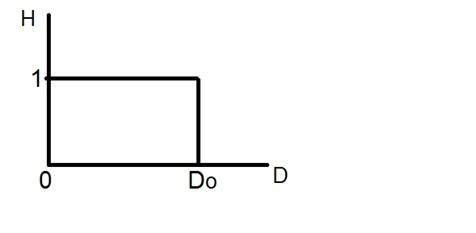
นี่คือการแสดงตัวกรองความถี่ต่ำในอุดมคติ ณ จุดที่แน่นอนของ Do คุณไม่สามารถบอกได้ว่าค่าจะเป็น 0 หรือ 1 เนื่องจากเอฟเฟกต์เสียงเรียกเข้าจะปรากฏที่จุดนั้น
ดังนั้นเพื่อลดเอฟเฟกต์ที่ปรากฏคือโลว์พาสในอุดมคติและฟิลเตอร์ความถี่สูงในอุดมคติจึงมีการนำตัวกรองความถี่ต่ำแบบเกาส์เซียนและตัวกรองความถี่สูงแบบเกาส์เซียนมาใช้
Gaussian Low pass filter
แนวคิดของการกรองและการส่งผ่านต่ำยังคงเหมือนเดิม แต่มีเพียงการเปลี่ยนแปลงเท่านั้นที่แตกต่างกันและราบรื่นมากขึ้น
ตัวกรองความถี่ต่ำ Gaussian สามารถแสดงเป็น

สังเกตการเปลี่ยนเส้นโค้งที่ราบรื่นเนื่องจากในแต่ละจุดค่าของ Do สามารถกำหนดได้อย่างแน่นอน
Gaussian high pass filter
ตัวกรองความถี่สูงแบบเกาส์เซียนมีแนวคิดเช่นเดียวกับฟิลเตอร์ความถี่สูงในอุดมคติ แต่อีกครั้งการเปลี่ยนจะราบรื่นกว่าเมื่อเทียบกับฟิลเตอร์ในอุดมคติ
ในบทช่วยสอนนี้เราจะพูดถึงช่องว่างสี
ช่องว่างสีคืออะไร?
ช่องว่างสีคือโหมดสีประเภทต่างๆที่ใช้ในการประมวลผลภาพและสัญญาณและระบบเพื่อวัตถุประสงค์ต่างๆ ช่องว่างสีทั่วไปบางส่วน ได้แก่ :
RGB
CMY’K
Y’UV
YIQ
Y’CbCr
HSV
RGB
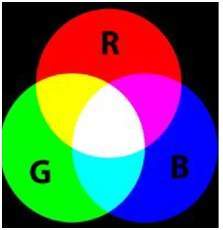
RGB เป็นพื้นที่สีที่ใช้กันอย่างแพร่หลายและเราได้พูดถึงเรื่องนี้ไปแล้วในบทช่วยสอนที่ผ่านมา RGB ย่อมาจากสีเขียวแดงและสีน้ำเงิน
สิ่งที่โมเดล RGB ระบุว่าภาพสีแต่ละภาพนั้นประกอบขึ้นจากภาพที่แตกต่างกันสามภาพ ภาพสีแดงภาพสีน้ำเงินและภาพสีดำ ภาพสีเทาปกติสามารถกำหนดได้ด้วยเมทริกซ์เดียว แต่จริงๆแล้วภาพสีประกอบด้วยเมทริกซ์ที่แตกต่างกันสามเมทริกซ์
เมทริกซ์ภาพสีเดียว = เมทริกซ์สีแดง + เมทริกซ์สีน้ำเงิน + เมทริกซ์สีเขียว
สิ่งนี้สามารถเห็นได้ดีที่สุดในตัวอย่างด้านล่างนี้
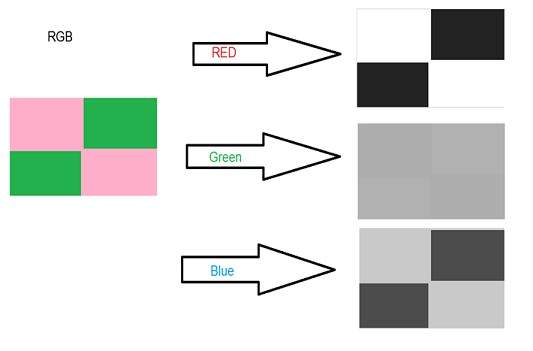
การใช้งาน RGB
การใช้งานทั่วไปของรุ่น RGB คือ
หลอดรังสีแคโทด (CRT)
จอแสดงผลคริสตัลเหลว (LCD)
Plasma Display หรือจอแสดงผล LED เช่นโทรทัศน์
จอภาพประมวลผลหรือหน้าจอขนาดใหญ่
CMYK

การแปลง RGB เป็น CMY
การแปลงจาก RGB เป็น CMY ทำได้โดยใช้วิธีนี้
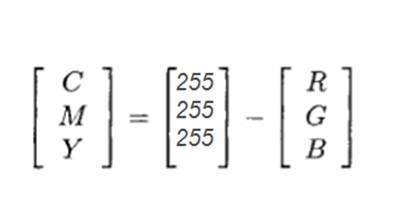
พิจารณาว่าคุณมีภาพสีหมายความว่าคุณมีอาร์เรย์ที่แตกต่างกันสามอาร์เรย์ ได้แก่ แดงเขียวและน้ำเงิน ตอนนี้ถ้าคุณต้องการแปลงเป็น CMY นี่คือสิ่งที่คุณต้องทำ คุณต้องลบมันด้วยจำนวนระดับสูงสุด - 1. แต่ละเมทริกซ์จะถูกลบและเมทริกซ์ CMY ตามลำดับจะเต็มไปด้วยผลลัพธ์
Y'UV
Y'UV กำหนดพื้นที่สีในรูปของหนึ่งลูมา (Y ') และสององค์ประกอบโครเมียม (UV) โมเดลสี Y'UV ใช้ในมาตรฐานวิดีโอสีผสมต่อไปนี้
NTSC (คณะกรรมการระบบโทรทัศน์แห่งชาติ)
PAL (เฟสสลับสาย)
SECAM (Sequential couleur a amemoire ภาษาฝรั่งเศสสำหรับ "สีตามลำดับพร้อมหน่วยความจำ)

Y'CbCr
โมเดลสี Y'CbCr ประกอบด้วย Y 'ส่วนประกอบของ luma และ cb และ cr เป็นส่วนประกอบของโครเมียมที่แตกต่างกันสีน้ำเงินและสีแดง
ไม่ใช่พื้นที่สีแน่นอน ส่วนใหญ่จะใช้กับระบบดิจิทัล
แอปพลิเคชันทั่วไป ได้แก่ การบีบอัด JPEG และ MPEG
Y'UV มักใช้เป็นคำสำหรับ Y'CbCr อย่างไรก็ตามรูปแบบที่แตกต่างกันโดยสิ้นเชิง ความแตกต่างที่สำคัญระหว่างสองสิ่งนี้คืออดีตเป็นอนาล็อกในขณะที่ภายหลังเป็นดิจิทัล

ในบทช่วยสอนสุดท้ายของการบีบอัดภาพเราจะพูดถึงเทคนิคบางอย่างที่ใช้ในการบีบอัด
เราจะพูดถึงการบีบอัด JPEG ซึ่งเป็นการบีบอัดแบบสูญเสียเนื่องจากข้อมูลบางส่วนสูญเสียไปในที่สุด
มาคุยกันก่อนว่าการบีบอัดภาพคืออะไร
การบีบอัดภาพ
การบีบอัดภาพเป็นวิธีการบีบอัดข้อมูลบนภาพดิจิทัล
วัตถุประสงค์หลักในการบีบอัดภาพคือ:
จัดเก็บข้อมูลในรูปแบบที่มีประสิทธิภาพ
ส่งข้อมูลในรูปแบบที่มีประสิทธิภาพ
การบีบอัดภาพอาจสูญเสียหรือไม่สูญเสีย
การบีบอัด JPEG
JPEG ย่อมาจากกลุ่มผู้เชี่ยวชาญด้านการถ่ายภาพร่วม เป็นมาตรฐานระหว่างประเทศแรกในการบีบอัดภาพ มีการใช้กันอย่างแพร่หลายในปัจจุบัน มันอาจจะสูญเสียและไม่สูญเสีย แต่เทคนิคที่เราจะพูดถึงในวันนี้คือเทคนิคการบีบอัดแบบสูญเสีย
การบีบอัด jpeg ทำงานอย่างไร:
ขั้นตอนแรกคือการแบ่งภาพออกเป็นบล็อกโดยแต่ละภาพมีขนาด 8 x8

สำหรับบันทึกบอกว่าภาพขนาด 8x8 นี้มีค่าต่อไปนี้
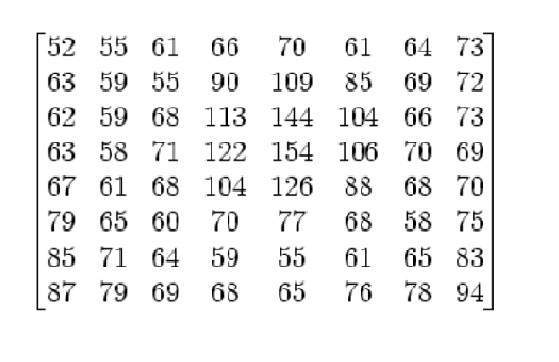
ช่วงของความเข้มของพิกเซลตอนนี้อยู่ระหว่าง 0 ถึง 255 เราจะเปลี่ยนช่วงจาก -128 เป็น 127
การลบ 128 ออกจากค่าพิกเซลแต่ละค่าจะให้ค่าพิกเซลตั้งแต่ -128 ถึง 127 หลังจากลบ 128 ออกจากค่าพิกเซลแต่ละค่าเราได้ผลลัพธ์ดังต่อไปนี้

ตอนนี้เราจะคำนวณโดยใช้สูตรนี้
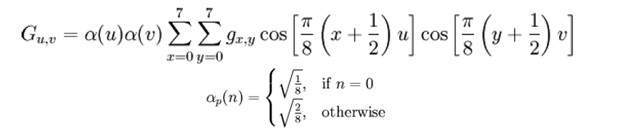
ผลลัพธ์มาจากสิ่งนี้ถูกเก็บไว้ในเมทริกซ์ A (j, k)
มีเมทริกซ์มาตรฐานที่ใช้สำหรับการคำนวณการบีบอัด JPEG ซึ่งกำหนดโดยเมทริกซ์ที่เรียกว่าเมทริกซ์ Luminance
เมทริกซ์นี้ได้รับด้านล่าง
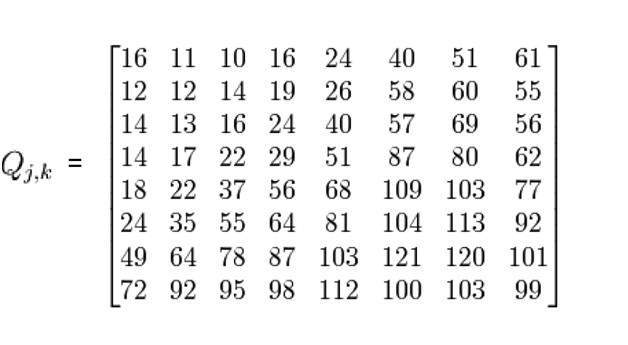
ใช้สูตรต่อไปนี้

เราได้ผลลัพธ์นี้หลังจากสมัคร

ตอนนี้เราจะดำเนินการเคล็ดลับจริงซึ่งทำในการบีบอัด JPEG ซึ่งเป็นการเคลื่อนไหว ZIG-ZAG ลำดับซิกแซกสำหรับเมทริกซ์ด้านบนแสดงไว้ด้านล่าง คุณต้องทำการซิกแซกจนกว่าคุณจะพบศูนย์ทั้งหมดข้างหน้า ดังนั้นภาพของเราจึงถูกบีบอัด

Summarizing JPEG compression
ขั้นตอนแรกคือการแปลงรูปภาพเป็น Y'CbCr และเพียงแค่เลือกช่อง Y 'และแบ่งเป็น 8 x 8 บล็อก จากนั้นเริ่มจากบล็อกแรกแมปช่วงตั้งแต่ -128 ถึง 127 หลังจากนั้นคุณต้องหาการแปลงฟูเรียร์แบบไม่ต่อเนื่องของเมทริกซ์ ผลลัพธ์ของสิ่งนี้ควรเป็นเชิงปริมาณ ขั้นตอนสุดท้ายคือการใช้การเข้ารหัสในลักษณะซิกแซกและทำจนกว่าคุณจะพบศูนย์ทั้งหมด
บันทึกอาร์เรย์หนึ่งมิติเท่านี้ก็เสร็จแล้ว
Note. You have to repeat this procedure for all the block of 8 x 8.
การรู้จำอักขระด้วยแสงมักจะย่อว่า OCR ซึ่งรวมถึงการแปลงภาพสแกนของภาพที่เขียนด้วยลายมือพิมพ์ดีดที่เขียนด้วยลายมือเป็นกลไกและทางไฟฟ้าให้เป็นข้อความของเครื่อง เป็นวิธีการทั่วไปในการแปลงข้อความที่พิมพ์เป็นดิจิทัลเพื่อให้สามารถค้นหาทางอิเล็กทรอนิกส์จัดเก็บให้กะทัดรัดยิ่งขึ้นแสดงบนบรรทัดและใช้ในกระบวนการของเครื่องจักรเช่นการแปลด้วยเครื่องข้อความเป็นคำพูดและการขุดข้อความ
ในช่วงไม่กี่ปีที่ผ่านมาเทคโนโลยี OCR (Optical Character Recognition) ได้ถูกนำไปใช้ในอุตสาหกรรมทั้งหมดซึ่งเป็นการปฏิวัติกระบวนการจัดการเอกสาร OCR ทำให้เอกสารที่สแกนกลายเป็นมากกว่าไฟล์รูปภาพโดยเปลี่ยนเป็นเอกสารที่ค้นหาได้ทั้งหมดพร้อมเนื้อหาข้อความที่คอมพิวเตอร์รู้จัก ด้วยความช่วยเหลือของ OCR ผู้คนไม่จำเป็นต้องพิมพ์เอกสารสำคัญซ้ำด้วยตนเองอีกต่อไปเมื่อป้อนลงในฐานข้อมูลอิเล็กทรอนิกส์ แต่ OCR จะดึงข้อมูลที่เกี่ยวข้องและป้อนโดยอัตโนมัติ ผลลัพธ์คือการประมวลผลข้อมูลที่ถูกต้องและมีประสิทธิภาพโดยใช้เวลาน้อยลง
การรู้จำอักขระด้วยแสงมีพื้นที่การวิจัยหลายด้าน แต่ส่วนที่พบมากที่สุดมีดังต่อไปนี้
Banking:
เขาใช้ OCR แตกต่างกันไปตามสาขาต่างๆ แอปพลิเคชั่นหนึ่งที่รู้จักกันอย่างแพร่หลายคือในด้านการธนาคารซึ่งใช้ OCR เพื่อประมวลผลการตรวจสอบโดยไม่ต้องมีมนุษย์เข้าไปเกี่ยวข้อง สามารถใส่เช็คลงในเครื่องได้การเขียนบนนั้นจะถูกสแกนทันทีและจำนวนเงินที่ถูกต้องจะถูกโอน เทคโนโลยีนี้เกือบจะสมบูรณ์แบบสำหรับการตรวจสอบที่พิมพ์แล้วและค่อนข้างแม่นยำสำหรับการตรวจสอบด้วยลายมือแม้ว่าจะต้องมีการยืนยันด้วยตนเองในบางครั้ง โดยรวมแล้วจะช่วยลดเวลารอในหลาย ๆ ธนาคาร
Blind and visually impaired persons:
ปัจจัยสำคัญประการหนึ่งในการเริ่มต้นการวิจัยเบื้องหลัง OCR คือนักวิทยาศาสตร์ต้องการสร้างคอมพิวเตอร์หรืออุปกรณ์ที่สามารถอ่านหนังสือให้คนตาบอดฟังได้ นักวิทยาศาสตร์วิจัยคนนี้ได้สร้างเครื่องสแกนแบบ Flatbed ซึ่งคนส่วนใหญ่รู้จักกันในชื่อเครื่องสแกนเอกสาร
Legal department:
ในอุตสาหกรรมกฎหมายมีการเคลื่อนไหวที่สำคัญในการแปลงเอกสารกระดาษให้เป็นดิจิทัล เพื่อประหยัดเนื้อที่และไม่จำเป็นต้องร่อนไฟล์กระดาษในกล่องเอกสารจะถูกสแกนและป้อนลงในฐานข้อมูลคอมพิวเตอร์ OCR ช่วยให้ขั้นตอนง่ายขึ้นโดยการทำให้เอกสารเป็นข้อความที่ค้นหาได้เพื่อให้ง่ายต่อการค้นหาและทำงานร่วมกับครั้งเดียวในฐานข้อมูล ปัจจุบันผู้เชี่ยวชาญด้านกฎหมายสามารถเข้าถึงไลบรารีเอกสารขนาดใหญ่ในรูปแบบอิเล็กทรอนิกส์ได้อย่างรวดเร็วและง่ายดายซึ่งสามารถค้นหาได้ง่ายๆโดยพิมพ์คำหลักไม่กี่คำ
Retail Industry:
เทคโนโลยีการจดจำบาร์โค้ดยังเกี่ยวข้องกับ OCR เราเห็นการใช้เทคโนโลยีนี้ในการใช้งานทั่วไปในแต่ละวัน
Other Uses:
OCR ใช้กันอย่างแพร่หลายในสาขาอื่น ๆ รวมถึงการศึกษาการเงินและหน่วยงานของรัฐ OCR ได้จัดทำตำราออนไลน์นับไม่ถ้วนช่วยประหยัดเงินสำหรับนักเรียนและช่วยให้สามารถแบ่งปันความรู้ได้ แอปพลิเคชันการถ่ายภาพใบแจ้งหนี้ถูกนำมาใช้ในหลาย ๆ ธุรกิจเพื่อติดตามบันทึกทางการเงินและป้องกันไม่ให้มีการค้างชำระ ในหน่วยงานของรัฐและองค์กรอิสระ OCR ช่วยลดความยุ่งยากในการรวบรวมและวิเคราะห์ข้อมูลรวมถึงกระบวนการอื่น ๆ ในขณะที่เทคโนโลยีพัฒนาอย่างต่อเนื่องจึงพบแอปพลิเคชั่นสำหรับเทคโนโลยี OCR มากขึ้นเรื่อย ๆ รวมถึงการใช้การจดจำลายมือที่เพิ่มขึ้น
วิสัยทัศน์คอมพิวเตอร์
การมองเห็นของคอมพิวเตอร์เกี่ยวข้องกับการสร้างแบบจำลองและการจำลองการมองเห็นของมนุษย์โดยใช้ซอฟต์แวร์คอมพิวเตอร์และฮาร์ดแวร์ อย่างเป็นทางการถ้าเรากำหนดวิสัยทัศน์ของคอมพิวเตอร์คำจำกัดความของมันก็คือการมองเห็นของคอมพิวเตอร์เป็นระเบียบวินัยที่ศึกษาวิธีสร้างใหม่ขัดขวางและทำความเข้าใจฉาก 3 มิติจากภาพ 2 มิติในแง่ของคุณสมบัติของโครงสร้างที่มีอยู่ในฉาก
ต้องการความรู้จากสาขาต่อไปนี้เพื่อที่จะเข้าใจและกระตุ้นการทำงานของระบบการมองเห็นของมนุษย์
วิทยาศาสตร์คอมพิวเตอร์
วิศวกรรมไฟฟ้า
Mathematics
Physiology
Biology
วิทยาศาสตร์ความรู้ความเข้าใจ
ลำดับชั้นของวิสัยทัศน์คอมพิวเตอร์:
การมองเห็นคอมพิวเตอร์แบ่งออกเป็นสามประเภทพื้นฐานดังต่อไปนี้:
การมองเห็นระดับต่ำ: รวมภาพกระบวนการสำหรับการแยกคุณลักษณะ
การมองเห็นระดับกลาง: รวมถึงการรับรู้วัตถุและการตีความฉาก 3 มิติ
วิสัยทัศน์ระดับสูง: รวมถึงการอธิบายแนวคิดของฉากเช่นกิจกรรมความตั้งใจและพฤติกรรม
สาขาที่เกี่ยวข้อง:
Computer Vision ทับซ้อนกันอย่างมีนัยสำคัญกับฟิลด์ต่อไปนี้:
การประมวลผลภาพ: เน้นไปที่การจัดการภาพ
การจดจำรูปแบบ: ศึกษาเทคนิคต่างๆในการจำแนกรูปแบบ
Photogrammetry: เกี่ยวข้องกับการได้รับการวัดที่แม่นยำจากภาพ
Computer Vision Vs การประมวลผลภาพ:
การประมวลผลภาพศึกษาภาพไปสู่การแปลงภาพ อินพุตและเอาต์พุตของการประมวลผลภาพมีทั้งรูปภาพ
การมองเห็นด้วยคอมพิวเตอร์คือการสร้างคำอธิบายที่ชัดเจนและมีความหมายของวัตถุทางกายภาพจากภาพของมัน ผลลัพธ์ของการมองเห็นด้วยคอมพิวเตอร์คือคำอธิบายหรือการตีความโครงสร้างในฉาก 3 มิติ
ตัวอย่างการใช้งาน:
Robotics
Medicine
Security
Transportation
ระบบอัตโนมัติอุตสาหกรรม
การประยุกต์ใช้หุ่นยนต์:
การแปลกำหนดตำแหน่งหุ่นยนต์โดยอัตโนมัติ
Navigation
หลีกเลี่ยงอุปสรรค
การประกอบ (การเจาะรูการเชื่อมการทาสี)
การจัดการ (เช่นหุ่นยนต์บังคับ PUMA)
Human Robot Interaction (HRI): หุ่นยนต์อัจฉริยะเพื่อโต้ตอบและให้บริการผู้คน
ใบสมัครยา:
การจำแนกประเภทและการตรวจหา (เช่นการจำแนกรอยโรคหรือเซลล์และการตรวจหาเนื้องอก)
การแบ่งส่วน 2D / 3D
การสร้างอวัยวะใหม่ของมนุษย์ 3 มิติ (MRI หรืออัลตราซาวนด์)
การผ่าตัดด้วยหุ่นยนต์นำทางด้วยสายตา
แอปพลิเคชันระบบอัตโนมัติทางอุตสาหกรรม:
การตรวจสอบอุตสาหกรรม (การตรวจจับข้อบกพร่อง)
Assembly
การอ่านฉลากบาร์โค้ดและแพ็คเกจ
การจัดเรียงวัตถุ
ความเข้าใจเอกสาร (เช่น OCR)
แอปพลิเคชันความปลอดภัย:
ไบโอเมตริกซ์ (ม่านตาพิมพ์ลายนิ้วมือจดจำใบหน้า)
การเฝ้าระวัง - ตรวจจับกิจกรรมหรือพฤติกรรมที่น่าสงสัยบางอย่าง
ใบสมัครการขนส่ง:
รถยนต์ที่เป็นอิสระ
ความปลอดภัยเช่นการตรวจสอบความระมัดระวังของผู้ขับขี่
คอมพิวเตอร์กราฟิก
คอมพิวเตอร์กราฟิกเป็นภาพกราฟิกที่สร้างขึ้นโดยใช้คอมพิวเตอร์และการนำเสนอข้อมูลภาพโดยคอมพิวเตอร์โดยเฉพาะด้วยความช่วยเหลือจากฮาร์ดแวร์และซอฟต์แวร์กราฟิกเฉพาะ โดยปกติเราสามารถพูดได้ว่าคอมพิวเตอร์กราฟิกคือการสร้างการจัดการและการจัดเก็บวัตถุทางเรขาคณิต (การสร้างแบบจำลอง) และภาพ (การแสดงผล)
สาขาคอมพิวเตอร์กราฟิกที่พัฒนาขึ้นพร้อมกับการเกิดขึ้นของฮาร์ดแวร์คอมพิวเตอร์กราฟิก ปัจจุบันคอมพิวเตอร์กราฟิกถูกใช้ในเกือบทุกสาขา เครื่องมือที่มีประสิทธิภาพมากมายได้รับการพัฒนาเพื่อแสดงภาพข้อมูล สาขาคอมพิวเตอร์กราฟิกได้รับความนิยมมากขึ้นเมื่อ บริษัท ต่างๆเริ่มใช้มันในวิดีโอเกม ปัจจุบันเป็นอุตสาหกรรมที่มีมูลค่าหลายพันล้านดอลลาร์และเป็นแรงผลักดันหลักเบื้องหลังการพัฒนาคอมพิวเตอร์กราฟิก พื้นที่การใช้งานทั่วไปบางส่วนมีดังต่อไปนี้:
การออกแบบโดยใช้คอมพิวเตอร์ช่วย (CAD)
กราฟิกการนำเสนอ
ภาพเคลื่อนไหว 3 มิติ
การศึกษาและการฝึกอบรม
อินเทอร์เฟซผู้ใช้แบบกราฟิก
การออกแบบโดยใช้คอมพิวเตอร์ช่วย:
ใช้ในการออกแบบอาคารรถยนต์เครื่องบินและสินค้าอื่น ๆ อีกมากมาย
ใช้ทำระบบเสมือนจริง
กราฟิกการนำเสนอ:
นิยมใช้ในการสรุปข้อมูลทางการเงินสถิติ
ใช้สร้างสไลด์
ภาพเคลื่อนไหว 3 มิติ:
ใช้อย่างมากในอุตสาหกรรมภาพยนตร์โดย บริษัท ต่างๆเช่น Pixar, DresmsWorks
เพื่อเพิ่มเอฟเฟกต์พิเศษในเกมและภาพยนตร์
การศึกษาและการฝึกอบรม:
คอมพิวเตอร์สร้างแบบจำลองของระบบทางกายภาพ
การแสดงภาพทางการแพทย์
3D MRI
การสแกนฟันและกระดูก
เครื่องกระตุ้นการฝึกนักบินเป็นต้น
อินเทอร์เฟซผู้ใช้แบบกราฟิก:
ใช้เพื่อสร้างอินเทอร์เฟซผู้ใช้แบบกราฟิกเช่นปุ่มไอคอนและส่วนประกอบอื่น ๆ