ซีรีส์ฟูเรียร์และทรานส์ฟอร์ม
ในบทช่วยสอนล่าสุดของการวิเคราะห์โดเมนความถี่เราได้พูดคุยกันว่าอนุกรมฟูริเยร์และการแปลงฟูริเยร์ใช้เพื่อแปลงสัญญาณเป็นโดเมนความถี่
ฟูเรียร์
ฟูเรียร์เป็นนักคณิตศาสตร์ในปี 1822 เขาให้อนุกรมฟูริเยร์และการแปลงฟูเรียร์เพื่อแปลงสัญญาณเป็นโดเมนความถี่
ซีรี่ส์ฟูเรียร์
อนุกรมฟูริเยร์ระบุว่าสัญญาณเป็นระยะสามารถแสดงเป็นผลรวมของไซน์และโคไซน์เมื่อคูณด้วยน้ำหนักที่แน่นอนนอกจากนี้ยังระบุว่าสัญญาณเป็นระยะสามารถแบ่งออกเป็นสัญญาณเพิ่มเติมได้ด้วยคุณสมบัติต่อไปนี้
- สัญญาณคือไซน์และโคไซน์
- สัญญาณเป็นฮาร์มอนิกของกันและกัน
สามารถดูเป็นภาพได้
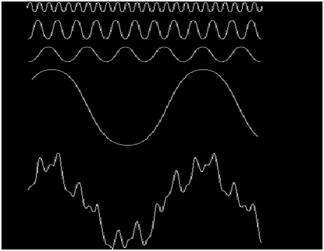
ในสัญญาณข้างต้นสัญญาณสุดท้ายคือผลรวมของสัญญาณข้างต้นทั้งหมด นี่คือความคิดของฟูเรียร์
คำนวณอย่างไร
เนื่องจากดังที่เราได้เห็นในโดเมนความถี่นั้นในการประมวลผลภาพในโดเมนความถี่เราจำเป็นต้องแปลงภาพโดยใช้เป็นโดเมนความถี่ก่อนและเราต้องใช้เวลาผกผันของผลลัพธ์เพื่อแปลงกลับเป็นโดเมนเชิงพื้นที่ นั่นเป็นเหตุผลที่ทั้งอนุกรมฟูริเยร์และการแปลงฟูเรียร์มีสองสูตร หนึ่งสำหรับการแปลงและอีกอันแปลงกลับเป็นโดเมนเชิงพื้นที่
อนุกรมฟูริเยร์
อนุกรมฟูริเยร์สามารถแสดงได้ด้วยสูตรนี้
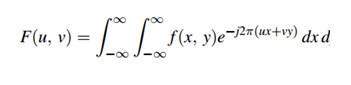
สูตรนี้สามารถคำนวณผกผันได้
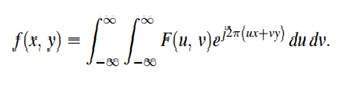
การแปลงฟูเรียร์
การแปลงฟูริเยร์ระบุว่าสัญญาณที่ไม่ใช่คาบที่มีพื้นที่ใต้เส้นโค้ง จำกัด สามารถแสดงเป็นปริพันธ์ของไซน์และโคไซน์ได้หลังจากคูณด้วยน้ำหนักที่แน่นอน
การแปลงฟูริเยร์มีแอพพลิเคชั่นที่หลากหลายซึ่งรวมถึงการบีบอัดภาพ (เช่นการบีบอัด JPEG) การกรองและการวิเคราะห์ภาพ
ความแตกต่างระหว่างอนุกรมฟูริเยร์และการแปลง
แม้ว่าอนุกรมฟูริเยร์และการแปลงฟูริเยร์จะได้รับจากฟูริเยร์ แต่ความแตกต่างระหว่างอนุกรมฟูริเยร์นั้นใช้กับสัญญาณเป็นระยะและการแปลงฟูริเยร์จะใช้กับสัญญาณที่ไม่ใช่คาบ
ใช้อันไหนกับภาพ
ตอนนี้คำถามคือว่าจะใช้อันไหนกับภาพอนุกรมฟูริเยร์หรือการแปลงฟูริเยร์ คำตอบสำหรับคำถามนี้อยู่ที่ความจริงที่ว่าภาพคืออะไร รูปภาพไม่เป็นระยะ และเนื่องจากภาพไม่เป็นระยะดังนั้นการแปลงฟูริเยร์จึงถูกใช้เพื่อแปลงเป็นโดเมนความถี่
การแปลงฟูเรียร์แบบไม่ต่อเนื่อง
เนื่องจากเรากำลังจัดการกับภาพและในความเป็นจริงภาพดิจิทัลดังนั้นสำหรับภาพดิจิทัลเราจะดำเนินการเกี่ยวกับการแปลงฟูเรียร์แบบไม่ต่อเนื่อง

พิจารณาระยะฟูเรียร์ข้างต้นของไซน์ ประกอบด้วยสามสิ่ง
- ความถี่เชิงพื้นที่
- Magnitude
- Phase
ความถี่เชิงพื้นที่เกี่ยวข้องโดยตรงกับความสว่างของภาพ ขนาดของไซนัสเกี่ยวข้องโดยตรงกับความเปรียบต่าง คอนทราสต์คือความแตกต่างระหว่างความเข้มพิกเซลสูงสุดและต่ำสุด เฟสมีข้อมูลสี
สูตรสำหรับการแปลงฟูเรียร์แบบไม่ต่อเนื่อง 2 มิติได้รับด้านล่าง
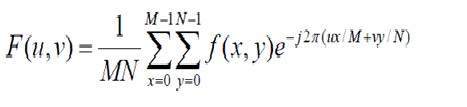
การแปลงฟูเรียร์แบบไม่ต่อเนื่องคือการแปลงฟูเรียร์ตัวอย่างดังนั้นจึงมีตัวอย่างบางส่วนที่แสดงถึงรูปภาพ ในสูตรด้านบน f (x, y) แสดงถึงรูปภาพและ F (u, v) หมายถึงการแปลงฟูเรียร์แบบไม่ต่อเนื่อง สูตรสำหรับการแปลงฟูเรียร์แบบไม่ต่อเนื่องผกผัน 2 มิติได้รับด้านล่าง
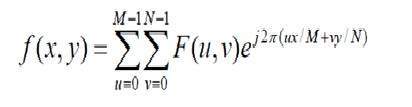
การแปลงฟูริเยร์แบบไม่ต่อเนื่องผกผันจะแปลงการแปลงฟูเรียร์กลับไปเป็นรูปภาพ
พิจารณาสัญญาณนี้
ตอนนี้เราจะเห็นภาพซึ่งเราจะคำนวณสเปกตรัมขนาด FFT จากนั้นเปลี่ยนขนาดสเปกตรัม FFT จากนั้นเราจะนำ Log ของสเปกตรัมที่เลื่อนนั้น
ภาพต้นฉบับ

ฟูริเยร์เปลี่ยนขนาดสเปกตรัม

การเปลี่ยนรูปแบบ Shifted Fourier

สเปกตรัมขนาดที่เปลี่ยนไป
