การแปลงภาพ
ก่อนที่เราจะพูดถึงการเปลี่ยนแปลงภาพคืออะไรเราจะพูดถึงการเปลี่ยนแปลงคืออะไร
การเปลี่ยนแปลง
การเปลี่ยนแปลงเป็นหน้าที่ ฟังก์ชันที่จับคู่ชุดหนึ่งกับอีกชุดหนึ่งหลังจากดำเนินการบางอย่าง
ระบบประมวลผลภาพดิจิตอล
เราได้เห็นแล้วในบทแนะนำเบื้องต้นว่าในการประมวลผลภาพดิจิทัลเราจะพัฒนาระบบที่อินพุตจะเป็นรูปภาพและเอาต์พุตจะเป็นรูปภาพด้วย และระบบจะดำเนินการประมวลผลภาพอินพุตและให้เอาต์พุตเป็นภาพที่ประมวลผล ดังแสดงด้านล่าง
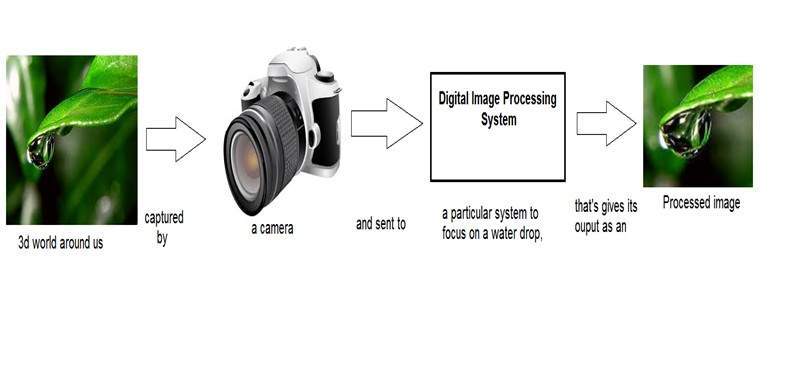
ฟังก์ชัน Now ที่ใช้ภายในระบบดิจิทัลนี้ซึ่งประมวลผลรูปภาพและแปลงเป็นเอาต์พุตสามารถเรียกได้ว่าเป็นฟังก์ชันการแปลง
ตามที่แสดงการแปลงหรือความสัมพันธ์วิธีที่รูปภาพ 1 ถูกแปลงเป็นรูปภาพ 2
การเปลี่ยนแปลงภาพ
พิจารณาสมการนี้
ก (x, y) = T {f (x, y)}
ในสมการนี้
F (x, y) = ภาพอินพุตที่ต้องใช้ฟังก์ชันการแปลง
G (x, y) = ภาพที่ส่งออกหรือภาพที่ประมวลผล
T คือฟังก์ชันการเปลี่ยนแปลง
ความสัมพันธ์ระหว่างอิมเมจอินพุตและอิมเมจเอาต์พุตที่ประมวลผลสามารถแสดงเป็น
s = T (r)
โดยที่ r คือค่าพิกเซลหรือความเข้มระดับสีเทาของ f (x, y) ณ จุดใด ๆ และ s คือค่าพิกเซลหรือความเข้มระดับสีเทาของ g (x, y) ณ จุดใด ๆ
การแปลงระดับสีเทาพื้นฐานได้รับการกล่าวถึงในบทช่วยสอนของเราเกี่ยวกับการแปลงระดับสีเทาขั้นพื้นฐาน
ตอนนี้เราจะพูดถึงฟังก์ชั่นการแปลงขั้นพื้นฐานบางอย่าง
ตัวอย่าง
พิจารณาฟังก์ชันการเปลี่ยนแปลงนี้
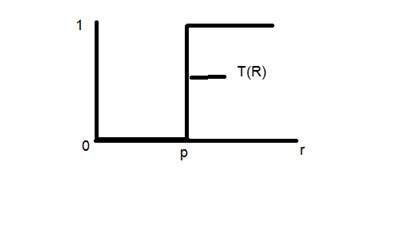
ให้จุด r เป็น 256 และจุด p เป็น 127 พิจารณาว่าภาพนี้เป็นภาพ bpp หนึ่งภาพ นั่นหมายความว่าเรามีความเข้มเพียง 2 ระดับนั่นคือ 0 และ 1 ดังนั้นในกรณีนี้การเปลี่ยนแปลงที่แสดงโดยกราฟสามารถอธิบายได้ว่า
ค่าความเข้มของพิกเซลทั้งหมดที่ต่ำกว่า 127 (จุด p) เป็น 0 หมายถึงสีดำ และค่าความเข้มพิกเซลทั้งหมดที่มากกว่า 127 เท่ากับ 1 นั่นหมายถึงสีขาว แต่เมื่อถึงจุด 127 มีการเปลี่ยนแปลงอย่างกะทันหันดังนั้นเราจึงไม่สามารถบอกได้ว่า ณ จุดนั้นแน่นอนค่าจะเป็น 0 หรือ 1
ในทางคณิตศาสตร์ฟังก์ชันการเปลี่ยนแปลงนี้สามารถแสดงเป็น:
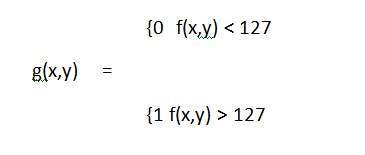
ลองพิจารณาการเปลี่ยนแปลงอื่นเช่นนี้
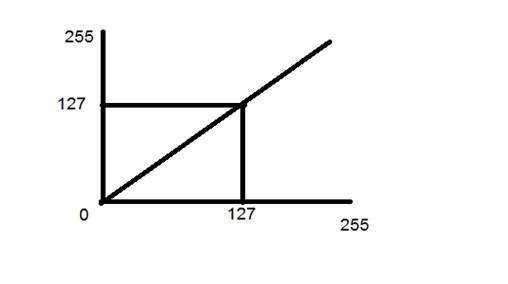
ตอนนี้ถ้าคุณจะดูกราฟนี้คุณจะเห็นเส้นตรงระหว่างภาพอินพุตและภาพเอาต์พุต
แสดงว่าสำหรับแต่ละพิกเซลหรือค่าความเข้มของภาพอินพุตมีค่าความเข้มของภาพที่ส่งออกเท่ากัน นั่นหมายความว่าภาพที่ส่งออกเป็นภาพจำลองที่แน่นอนของภาพอินพุต
สามารถแสดงทางคณิตศาสตร์เป็น:
ก. (x, y) = f (x, y)
ภาพอินพุตและเอาต์พุตจะอยู่ในกรณีนี้ดังแสดงด้านล่าง
