สะพาน AC
ในบทนี้ให้เราพูดคุยเกี่ยวกับสะพาน AC ซึ่งสามารถใช้ในการวัดความเหนี่ยวนำได้ สะพานไฟฟ้ากระแสสลับทำงานโดยใช้สัญญาณแรงดันไฟฟ้ากระแสสลับเท่านั้น circuit diagram ของสะพาน AC แสดงดังรูปด้านล่าง
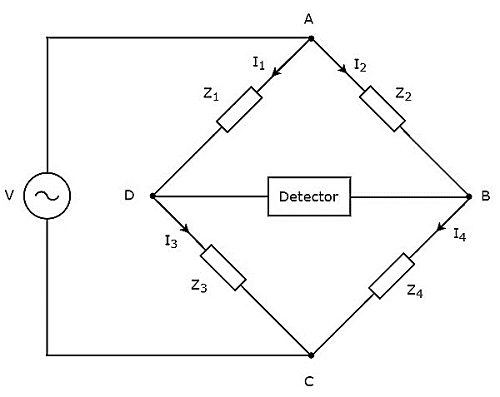
ดังแสดงในรูปด้านบนสะพาน AC ส่วนใหญ่ประกอบด้วยสี่แขนซึ่งเชื่อมต่อกันในรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขนทั้งหมดนี้ประกอบด้วยอิมพีแดนซ์บางส่วน
นอกจากนี้ยังต้องใช้เครื่องตรวจจับและแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับเพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่รู้จัก ดังนั้นหนึ่งในสองตัวนี้วางอยู่ในแนวทแยงมุมของสะพาน AC หนึ่งเส้นและอีกอันหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน AC สภาพสมดุลของสะพานวีทสโตนเป็น -
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
เราจะได้รับไฟล์ balancing condition of AC bridgeเพียงแค่แทนที่ R ด้วย Z ในสมการด้านบน
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
ที่นี่ $ Z_ {1} $ และ $ Z_ {2} $ เป็นอิมพีแดนซ์คงที่ ในขณะที่ $ Z_ {3} $ เป็นอิมพีแดนซ์ตัวแปรมาตรฐานและ $ Z_ {4} $ เป็นอิมพีแดนซ์ที่ไม่รู้จัก
Note - เราสามารถเลือกอิมพีแดนซ์สองตัวจากสี่ตัวนั้นเป็นอิมพีแดนซ์คงที่อิมพีแดนซ์ตัวหนึ่งเป็นอิมพีแดนซ์ตัวแปรมาตรฐานและอิมพีแดนซ์อื่น ๆ เป็นอิมพีแดนซ์ที่ไม่รู้จักตามการใช้งาน
ต่อไปนี้เป็นสะพาน AC สองตัวซึ่งสามารถใช้วัดได้ inductance.
- สะพาน Maxwell
- สะพาน Hay
ตอนนี้ให้เราพูดคุยเกี่ยวกับสะพาน AC สองตัวนี้ทีละตัว
สะพาน Maxwell
สะพานของ Maxwell เป็นสะพาน AC ที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขนสองข้างของสะพานนี้ประกอบด้วยตัวต้านทานเดี่ยวแขนข้างหนึ่งประกอบด้วยชุดตัวต้านทานและตัวเหนี่ยวนำและแขนอีกข้างประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกัน
เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับใช้เพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่รู้จัก ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของ Maxwell และอีกอันหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน Maxwell
สะพานของ Maxwell ใช้ในการวัดค่าของความเหนี่ยวนำขนาดกลาง circuit diagram ของสะพาน Maxwell แสดงไว้ในรูปด้านล่าง
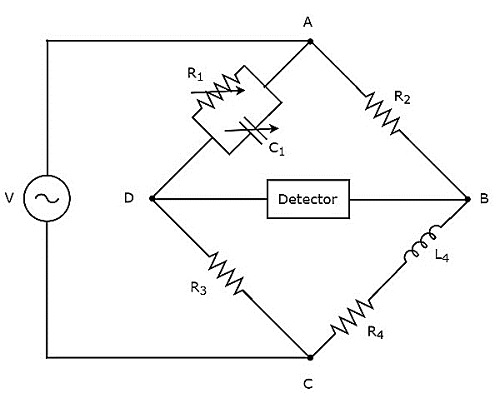
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือสี่เหลี่ยม แขน AB และ CD ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ตามลำดับ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ แขน DA ประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ สมการ 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ สมการ 2
โดยการแทนค่าของตัวต้านทาน $ R_ {1} $, $ R_ {2} $ และ $ R_ {3} $ ในสมการ 1 เราจะได้ค่าตัวต้านทาน $ R_ {4} $ ในทำนองเดียวกันโดยการแทนค่าของตัวเก็บประจุ $ C_ {1} $ และค่าของตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ในสมการ 2 เราจะได้ค่าตัวเหนี่ยวนำ $ L_ {4 } $.
advantage ของสะพานของ Maxwell คือทั้งค่าของตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ จะไม่ขึ้นกับค่าของความถี่
สะพาน Hay
Hay's bridge เป็นบริดจ์รุ่นดัดแปลงของ Maxwell ซึ่งเราได้รับโดยการปรับเปลี่ยนแขนซึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานเข้ากับแขนซึ่งประกอบด้วยชุดตัวต้านทานและตัวเก็บประจุในสะพานของ Maxwell
สะพาน Hay ใช้ในการวัดค่าของความเหนี่ยวนำสูง circuit diagram ของสะพาน Hay แสดงไว้ในรูปด้านล่าง
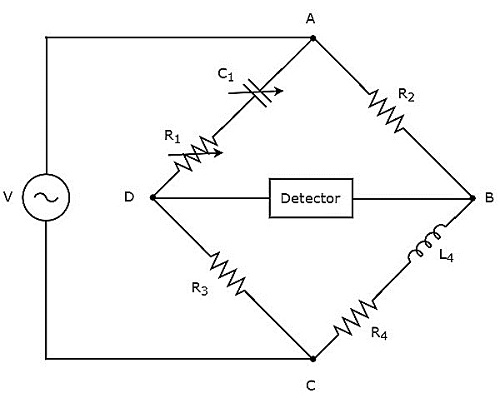
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือสี่เหลี่ยม แขน AB และ CD ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ตามลำดับ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ แขน DA ประกอบด้วยชุดตัวต้านทาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ โอเมก้า C_ {1}} \ right)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $
คูณตัวเศษและตัวส่วนของเงื่อนไขด้านขวามือของสมการข้างบนด้วย $ 1 - j \ omega R_ {1} C_ {1} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ โอเมก้า R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ โอเมก้า ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ สมการ 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ สมการ 4
โดยการแทนค่าของ $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ และ $ \ omega $ ในสมการ 3 และสมการ 4 เราจะได้ค่าของตัวต้านทาน $ R_ {4 } $ และตัวเหนี่ยวนำ $ L_ {4} $