โพรบ CRO

เราสามารถเชื่อมต่อวงจรทดสอบใด ๆ เข้ากับออสซิลโลสโคปผ่านหัววัด เนื่องจาก CRO เป็นออสซิลโลสโคปพื้นฐานจึงเรียกโพรบที่เชื่อมต่ออยู่ด้วยCRO probe.

เราควรเลือกโพรบในลักษณะที่ไม่ควรสร้างปัญหาในการโหลดกับวงจรทดสอบ เพื่อให้เราสามารถวิเคราะห์วงจรทดสอบด้วยสัญญาณได้อย่างถูกต้องบนหน้าจอ CRO

โพรบ CRO ควรมีดังต่อไปนี้ characteristics.

• ความต้านทานสูง
• แบนด์วิดท์สูง

block diagram ของโพรบ CRO แสดงไว้ในรูปด้านล่าง

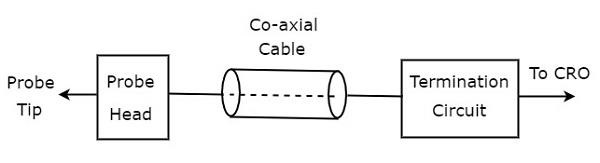
ดังแสดงในรูปหัววัด CRO ส่วนใหญ่ประกอบด้วยสามบล็อก คือหัวโพรบสายแกนร่วมและวงจรเลิกจ้าง สายเคเบิลแกนร่วมเพียงแค่เชื่อมต่อหัวโพรบและวงจรเลิกจ้าง

ประเภทของ CRO Probes

หัววัด CRO สามารถแบ่งออกได้ดังต่อไปนี้ two types.

• Passive Probes
• Active Probes

ตอนนี้ให้เราพูดคุยเกี่ยวกับโพรบทั้งสองประเภทนี้ทีละประเภท

Passive Probes

หากหัวโพรบประกอบด้วยองค์ประกอบแบบพาสซีฟจะเรียกว่า passive probe. แผนภาพวงจรของโพรบแบบพาสซีฟแสดงไว้ในรูปด้านล่าง

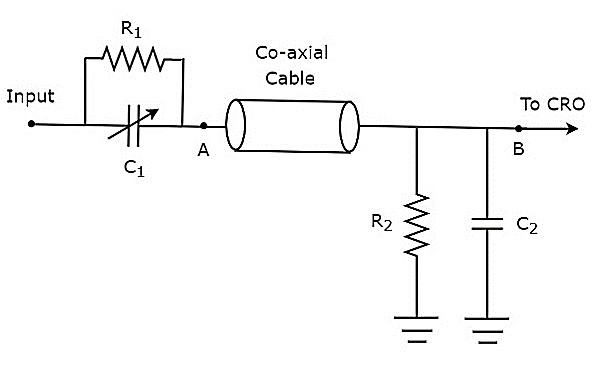
ดังแสดงในรูปหัวโพรบประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุแบบแปรผัน $ C_ {1} $ ในทำนองเดียวกันวงจรเลิกจ้างประกอบด้วยชุดตัวต้านทานแบบขนาน $ R_ {2} $ และตัวเก็บประจุ $ C_ {2} $

แผนภาพวงจรข้างต้นได้รับการแก้ไขในรูปแบบของ bridge circuit และแสดงในรูปด้านล่าง

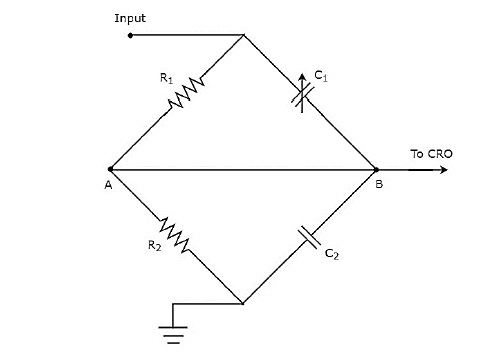
เราสามารถบาลานซ์บริดจ์ได้โดยการปรับค่าของตัวเก็บประจุแบบแปรผัน $ c_ {1} $ เราจะพูดถึงแนวคิดของสะพานในบทต่อไปนี้ ในขณะนี้ให้พิจารณาสิ่งต่อไปนี้balancing condition of AC bridge.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

Substitute, อิมพีแดนซ์ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เท่ากับ $ R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ { 2} $ และ $ \ frac {1} {j \ omega C_ {2}} $ ตามลำดับในสมการด้านบน

$$ R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ right) R_ {2 } $$

$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $ สมการ 1

ตามหลักการแบ่งแรงดันเราจะได้ voltage across resistor, $R_{2}$ เช่น

$$ V_ {0} = V_ {i} \ left (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ right) $$

attenuation factorคืออัตราส่วนของแรงดันไฟฟ้าอินพุต $ V_ {i} $ และแรงดันขาออก $ V_ {0} $ ดังนั้นจากสมการด้านบนเราจะได้ปัจจัยการลดทอน $ \ alpha $ as

$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$

$ \ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2} $ สมการ 2

จากสมการ 2 เราสามารถสรุปได้ว่าค่าของ $ R_ {1} $ มากกว่าหรือเท่ากับค่า 2 สำหรับค่าจำนวนเต็มของ $ \: \ alpha> 1 $

แทนสมการ 2 ในสมการ 1

$$ \ left (\ alpha-1 \ right) R_ {2} C_ {1} = R_ {2} C_ {2} $$

$ \ Rightarrow \ left (\ alpha-1 \ right) C_ {1} = C_ {2} $

$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)} $ สมการ 3

จากสมการ 3 เราสามารถสรุปได้ว่าค่าของ $ C_ {1} $ น้อยกว่าหรือเท่ากับค่า $ C_ {2} $ สำหรับค่าจำนวนเต็ม $ \ alpha> 1 $

Example

ให้เราหาค่า $ R_ {1} $ และ $ C_ {1} $ ของโพรบที่มีปัจจัยการลดทอน $ \ alpha $ เป็น 10 สมมติ $ R_ {2} = 1 M \ Omega $ และ $ C_ {2} = 18pF $.

• Step1 - เราจะได้รับค่า $ R_ {1} $ โดยแทนที่ค่าของ $ \ alpha $ และ $ R_ {2} $ ในสมการ 2

$$ R_ {1} = \ left (10-1 \ right) \ times 1 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 M \ Omega $$

Step 2 - เราจะได้รับค่า $ C_ {1} $ โดยแทนที่ค่าของ $ \ alpha $ และ $ C_ {2} $ ในสมการ 3

$$ C_ {1} = \ frac {18 \ times10 ^ {- 12}} {\ left (10-1 \ right)} $$

$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {- 12} $$

$$ \ Rightarrow C_ {1} = 2 pF $$

ดังนั้นค่าของ $ R_ {1} $ และ $ C_ {1} $ ของโพรบจะเป็น $ 9M \ Omega $ และ $ 2pF $ ตามลำดับสำหรับข้อกำหนดที่กำหนด

Active Probes

หากหัวโพรบประกอบด้วยชิ้นส่วนอิเล็กทรอนิกส์ที่ใช้งานอยู่จะเรียกว่า active probe. แผนภาพบล็อกของโพรบที่ใช้งานอยู่แสดงในรูปด้านล่าง

ดังแสดงในรูปหัวโพรบประกอบด้วยตัวติดตามแหล่งสัญญาณ FET ในน้ำตกที่มีตัวติดตามตัวปล่อย BJT ตัวติดตามแหล่งสัญญาณ FET ให้อิมพีแดนซ์อินพุตสูงและอิมพีแดนซ์เอาต์พุตต่ำ ในขณะที่วัตถุประสงค์ของผู้ติดตามตัวปล่อย BJT คือการหลีกเลี่ยงหรือกำจัดความไม่ตรงกันของอิมพีแดนซ์

อีกสองส่วนเช่นสายเคเบิลแกนร่วมและวงจรเลิกจ้างยังคงเหมือนเดิมทั้งในโพรบที่ใช้งานและแบบพาสซีฟ