สะพาน DC

DC bridgesสามารถใช้งานได้โดยใช้สัญญาณแรงดันไฟฟ้ากระแสตรงเท่านั้น สะพานกระแสตรงมีประโยชน์ในการวัดค่าของความต้านทานที่ไม่รู้จักซึ่งมีอยู่ในสะพาน Wheatstone's Bridge เป็นตัวอย่างของสะพาน DC

ตอนนี้ให้เราพูดคุยเกี่ยวกับ Wheatstone’s Bridge เพื่อหาค่าความต้านทานที่ไม่รู้จัก

สะพานวีทสโตน

สะพานวีทสโตนเป็นสะพานกระแสตรงซึ่งส่วนใหญ่มีแขนทั้งสี่ข้าง แขนทั้งสี่นี้เป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือรูปสี่เหลี่ยมจัตุรัสและแขนแต่ละข้างประกอบด้วยตัวต้านทานหนึ่งตัว

ในการหาค่าความต้านทานที่ไม่รู้จักเราต้องใช้กัลวาโนมิเตอร์และแหล่งจ่ายแรงดันไฟฟ้ากระแสตรง ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของวีทสโตนและอีกอันหนึ่งวางไว้ในแนวทแยงมุมของสะพานวีทสโตน

สะพานของวีทสโตนใช้ในการวัดค่าของความต้านทานปานกลาง circuit diagram ของสะพานวีทสโตนแสดงไว้ในรูปด้านล่าง

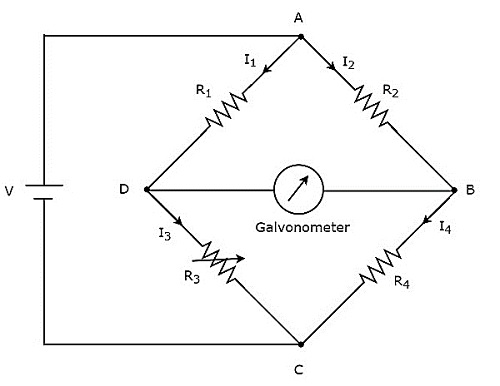
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็น a rhombusหรือรูปทรงสี่เหลี่ยม ประกอบด้วยตัวต้านทาน $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ และ $ R_ {1} $ ตามลำดับ ปล่อยให้กระแสที่ไหลผ่านแขนตัวต้านทานเหล่านี้คือ $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ และ $ I_ {1} $ ตามลำดับและทิศทางของกระแสเหล่านี้จะแสดงในรูป

แขนทแยงมุม DB และ AC ประกอบด้วยกัลวาโนมิเตอร์และแหล่งกำเนิดแรงดันไฟฟ้ากระแสตรงของโวลต์ V ตามลำดับ ที่นี่ตัวต้านทาน $ R_ {3} $ เป็นตัวต้านทานตัวแปรมาตรฐานและตัวต้านทาน $ R_ {4} $ เป็นตัวต้านทานที่ไม่รู้จัก เราทำได้balance the bridgeโดยการเปลี่ยนค่าความต้านทานของตัวต้านทาน $ R_ {3} $

วงจรสะพานด้านบนมีความสมดุลเมื่อไม่มีกระแสไหลผ่านแขนทแยงมุม DB นั่นหมายความว่ามีno deflection ในกัลวาโนมิเตอร์เมื่อสะพานสมดุล

สะพานจะสมดุลเมื่อต่อไปนี้ two conditions พอใจ

• แรงดันไฟฟ้าข้ามแขน AD เท่ากับแรงดันไฟฟ้าข้ามแขน AB กล่าวคือ

$$ V_ {AD} = V_ {AB} $$

$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ สมการ 1

• แรงดันไฟฟ้าข้ามแขน DC เท่ากับแรงดันไฟฟ้าข้ามแขน BC กล่าวคือ

$$ V_ {DC} = V_ {BC} $$

$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $ สมการ 2

จากเงื่อนไขสมดุลสองประการข้างต้นเราจะได้รับสิ่งต่อไปนี้ two conclusions.

• กระแสที่ไหลผ่านแขน AD จะเท่ากับของแขน DC กล่าวคือ

$$ I_ {1} = I_ {3} $$

• กระแสที่ไหลผ่านแขน AB จะเท่ากับแขน BC กล่าวคือ

$$ I_ {2} = I_ {4} $$

หาอัตราส่วนของสมการ 1 และสมการ 2

$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ สมการ 3

แทน $ I_ {1} = I_ {3} $ และ $ I_ {2} = I_ {4} $ ในสมการ 3

$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$

$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$

$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

โดยการแทนค่าที่ทราบของตัวต้านทาน $ R_ {1} $, $ R_ {2} $ และ $ R_ {3} $ ในสมการด้านบนเราจะได้ value of resistor,$R_{4}$.