คู่มือฉบับย่อ
เครื่องมือที่ใช้วัดปริมาณใด ๆ เรียกว่าเครื่องมือวัด บทช่วยสอนนี้ครอบคลุมส่วนใหญ่ในไฟล์electronic instrumentsซึ่งมีประโยชน์สำหรับการวัดปริมาณหรือพารามิเตอร์ทางไฟฟ้า
ต่อไปนี้เป็นเครื่องมืออิเล็กทรอนิกส์ที่ใช้บ่อยที่สุด
- Voltmeter
- Ammeter
- Ohmmeter
- Multimeter
ตอนนี้ให้เราพูดคุยเกี่ยวกับเครื่องมือเหล่านี้สั้น ๆ
โวลต์มิเตอร์
ตามชื่อ voltmeterเป็นเครื่องมือวัดที่วัดแรงดันไฟฟ้าข้ามจุดสองจุดของวงจรไฟฟ้า โวลต์มิเตอร์มีสองประเภท: โวลต์มิเตอร์ DC และโวลต์มิเตอร์ AC
DC โวลต์มิเตอร์จะวัดแรงดันไฟฟ้ากระแสตรงในจุดสองจุดของวงจรไฟฟ้าในขณะที่โวลต์มิเตอร์ AC จะวัดแรงดันไฟฟ้ากระแสสลับในสองจุดใด ๆ ของวงจรไฟฟ้า ตัวอย่างของpractical DC voltmeter ดังแสดงในรูปด้านล่าง

DC โวลต์มิเตอร์ที่แสดงในรูปด้านบนคือ a $(0-100)V$ DC voltmeter. ดังนั้นจึงสามารถใช้วัดแรงดันไฟฟ้ากระแสตรงจากศูนย์โวลต์ถึง 10 โวลต์
แอมมิเตอร์
ตามชื่อ ammeterเป็นเครื่องมือวัดที่ใช้วัดกระแสไฟฟ้าที่ไหลผ่านสองจุดของวงจรไฟฟ้า แอมป์มิเตอร์มีสองประเภท: แอมป์มิเตอร์ DC และแอมป์มิเตอร์ AC
แอมป์มิเตอร์ DC วัดกระแสไฟฟ้ากระแสตรงที่ไหลผ่านสองจุดของวงจรไฟฟ้า ในขณะที่แอมป์มิเตอร์ AC จะวัดกระแสไฟฟ้ากระแสสลับที่ไหลผ่านสองจุดของวงจรไฟฟ้า ตัวอย่างของpractical AC ammeter แสดงดังรูปด้านล่าง -

แอมป์มิเตอร์ AC ที่แสดงในรูปด้านบนคือ a $(0-100)A \:$ AC ammeter. ดังนั้นจึงสามารถใช้วัดกระแสไฟฟ้ากระแสสลับจากศูนย์แอมป์ถึง 100 แอมป์
โอห์มมิเตอร์
Ohmmeterใช้เพื่อวัดค่าความต้านทานระหว่างจุดสองจุดของวงจรไฟฟ้า นอกจากนี้ยังสามารถใช้เพื่อค้นหาค่าของตัวต้านทานที่ไม่รู้จัก โอห์มมิเตอร์มีสองประเภท ได้แก่ โอห์มมิเตอร์แบบอนุกรมและโอห์มมิเตอร์แบบปัด
ในโอห์มมิเตอร์ประเภทอนุกรมตัวต้านทานที่ไม่ทราบค่าและที่จะวัดควรเชื่อมต่อแบบอนุกรมกับโอห์มมิเตอร์ มันมีประโยชน์สำหรับการวัดhigh values of resistances.

ในโอห์มมิเตอร์ชนิด shunt ตัวต้านทานที่ไม่ทราบค่าและที่จะวัดควรเชื่อมต่อแบบขนาน (shunt) กับโอห์มมิเตอร์ มันมีประโยชน์สำหรับการวัดlow values of resistances.
ตัวอย่างของ practical shunt ohmmeterแสดงในรูปด้านบน โอห์มมิเตอร์ที่แสดงในรูปด้านบนคือ$(0-100)\Omega$ shunt ohmmeter. ดังนั้นจึงสามารถใช้เพื่อวัดค่าความต้านทานตั้งแต่ศูนย์โอห์มถึง 100 โอห์ม
มัลติมิเตอร์
Multimeterเป็นเครื่องมืออิเล็กทรอนิกส์ที่ใช้ในการวัดปริมาณเช่นแรงดันกระแสและความต้านทานทีละรายการ สามารถใช้ในการวัดแรงดันไฟฟ้ากระแสตรงและกระแสสลับกระแสตรงและกระแสสลับและความต้านทานในหลายช่วง มัลติมิเตอร์ที่ใช้งานได้จริงแสดงในรูปต่อไปนี้ -

ดังแสดงในรูปมัลติมิเตอร์นี้สามารถใช้ในการวัดความต้านทานสูงต่างๆความต้านทานต่ำแรงดันไฟฟ้ากระแสตรงแรงดันไฟฟ้ากระแสสลับกระแสตรงและกระแส AC มาตราส่วนและช่วงของค่าที่แตกต่างกันสำหรับแต่ละปริมาณเหล่านี้มีการระบุไว้ในรูปด้านบน
เครื่องมือที่เราพิจารณาในบทนี้ ได้แก่ indicating type instrumentsเนื่องจากตัวชี้ของเครื่องมือเหล่านี้เบี่ยงเบนและชี้ไปที่ค่าเฉพาะ เราจะพูดถึงเครื่องมือวัดอิเล็กทรอนิกส์เหล่านี้โดยละเอียดในบทต่อ ๆ ไป
ลักษณะของเครื่องมือวัดที่เป็นประโยชน์ในการทราบประสิทธิภาพของเครื่องมือและช่วยในการวัดปริมาณหรือพารามิเตอร์ใด ๆ เรียกว่า Performance Characteristics.
ประเภทของลักษณะการปฏิบัติงาน
ลักษณะการทำงานของเครื่องมือสามารถจำแนกได้ดังต่อไปนี้ two types.
- ลักษณะคงที่
- ลักษณะไดนามิก
ตอนนี้ให้เราพูดคุยเกี่ยวกับลักษณะสองประเภทนี้ทีละประเภท
ลักษณะคงที่
ลักษณะของปริมาณหรือพารามิเตอร์เครื่องมือวัดที่ do not varyเมื่อเทียบกับเวลาเรียกว่าลักษณะคงที่ บางครั้งปริมาณหรือพารามิเตอร์เหล่านี้อาจเปลี่ยนแปลงช้าตามเวลา ต่อไปนี้เป็นรายการของstatic characteristics.
- Accuracy
- Precision
- Sensitivity
- Resolution
- ข้อผิดพลาดคงที่
ตอนนี้ให้เราพูดคุยเกี่ยวกับลักษณะคงที่เหล่านี้ทีละคน
ความถูกต้อง
ความแตกต่างทางพีชคณิตระหว่างค่าที่ระบุของเครื่องมือ $ A_ {i} $ กับมูลค่าที่แท้จริง $ A_ {t} $ เรียกว่า accuracy. ในทางคณิตศาสตร์สามารถแสดงเป็น -
$$ ความแม่นยำ = A_ {i} - A_ {t} $$
คำว่าความแม่นยำหมายถึงมูลค่าที่ระบุของเครื่องมือ $ A_ {i} $ ใกล้เคียงกับมูลค่าที่แท้จริงมากขึ้นคือ $ A_ {t} $
ข้อผิดพลาดคงที่
ความแตกต่างระหว่างมูลค่าที่แท้จริง $ A_ {t} $ ของปริมาณที่ไม่แปรผันตามเวลาและมูลค่าที่ระบุของเครื่องมือ $ A_ {i} $ เรียกว่า static error, $ e_ {s} $. ในทางคณิตศาสตร์สามารถแสดงเป็น -
$$ e_ {s} = A_ {t} - A_ {i} $$
คำว่าข้อผิดพลาดคงหมายถึงความไม่ถูกต้องของเครื่องมือ หากข้อผิดพลาดคงที่แสดงในรูปของเปอร์เซ็นต์จะเรียกว่าpercentage of static error. ในทางคณิตศาสตร์สามารถแสดงเป็น -
$$ \% e_ {s} = \ frac {e_ {s}} {A_ {t}} \ times 100 $$
แทนค่า $ e_ {s} $ ทางขวามือของสมการด้านบน -
$$ \% e_ {s} = \ frac {A_ {t} - A_ {i}} {A_ {t}} \ times 100 $$
ที่ไหน
$ \% e_ {s} $ คือเปอร์เซ็นต์ของข้อผิดพลาดคงที่
ความแม่นยำ
หากเครื่องมือระบุค่าเดียวกันซ้ำ ๆ เมื่อใช้ในการวัดปริมาณเดียวกันภายใต้สถานการณ์เดียวกันในหลาย ๆ ครั้งเราสามารถพูดได้ว่าเครื่องมือนั้นมีค่าสูง precision.
ความไว
อัตราส่วนของการเปลี่ยนแปลงเอาต์พุต $ \ Delta A_ {out} $ ของเครื่องมือสำหรับการเปลี่ยนแปลงที่กำหนดในอินพุต $ \ Delta A_ {in} $ ที่จะวัดเรียกว่า sensitivity, S. ในทางคณิตศาสตร์สามารถแสดงเป็น -
$$ S = \ frac {\ Delta A_ {out}} {\ Delta A_ {in}} $$
คำว่าความไวหมายถึงการเปลี่ยนแปลงที่น้อยที่สุดในอินพุตที่วัดได้ซึ่งจำเป็นสำหรับเครื่องมือในการตอบสนอง
หากเส้นโค้งการปรับเทียบเป็น linearจากนั้นความไวของเครื่องมือจะเป็นค่าคงที่และเท่ากับความชันของเส้นโค้งการสอบเทียบ
หากเส้นโค้งการปรับเทียบเป็น non-linearจากนั้นความไวของเครื่องมือจะไม่เป็นค่าคงที่และจะแตกต่างกันไปตามอินพุต
ความละเอียด
หากเอาต์พุตของเครื่องมือจะเปลี่ยนก็ต่อเมื่อมีการเพิ่มขึ้นเฉพาะของอินพุตดังนั้นการเพิ่มขึ้นของอินพุตจะเรียกว่า Resolution. นั่นหมายความว่าเครื่องมือสามารถวัดอินพุตได้อย่างมีประสิทธิภาพเมื่อมีความละเอียดของอินพุต
ลักษณะไดนามิก
ลักษณะของเครื่องมือที่ใช้ในการวัดปริมาณหรือพารามิเตอร์ที่เปลี่ยนแปลงเร็วมากตามเวลาเรียกว่าลักษณะไดนามิก ต่อไปนี้เป็นรายการของdynamic characteristics.
- ความเร็วในการตอบสนอง
- ข้อผิดพลาดแบบไดนามิก
- Fidelity
- Lag
ตอนนี้ให้เราพูดคุยเกี่ยวกับลักษณะไดนามิกเหล่านี้ทีละคน
ความเร็วในการตอบสนอง
ความเร็วที่เครื่องมือตอบสนองเมื่อใดก็ตามที่มีการเปลี่ยนแปลงปริมาณที่จะวัดจะเรียกว่า speed of response. มันบ่งบอกว่าเครื่องมือนั้นเร็วแค่ไหน
ความล่าช้า
จำนวนความล่าช้าที่มีอยู่ในการตอบสนองของเครื่องมือเมื่อใดก็ตามที่มีการเปลี่ยนแปลงปริมาณที่จะวัดเรียกว่าการวัดความล่าช้า เรียกง่ายๆว่าlag.
ข้อผิดพลาดแบบไดนามิก
ความแตกต่างระหว่างมูลค่าที่แท้จริง $ A_ {t} $ ของปริมาณที่แปรผันตามเวลาและมูลค่าที่ระบุของเครื่องมือ $ A_ {i} $ เรียกว่าข้อผิดพลาดแบบไดนามิก $ e_ {d} $
ความซื่อสัตย์
ระดับที่เครื่องมือบ่งชี้ถึงการเปลี่ยนแปลงของปริมาณที่วัดได้โดยไม่มีข้อผิดพลาดแบบไดนามิกเรียกว่า Fidelity
ข้อผิดพลาดที่เกิดขึ้นระหว่างการวัดเรียกว่า measurement errors. ในบทนี้ให้เราพูดคุยเกี่ยวกับประเภทของข้อผิดพลาดในการวัด
ประเภทของข้อผิดพลาดในการวัด
เราสามารถจำแนกข้อผิดพลาดในการวัดออกเป็นสามประเภทดังต่อไปนี้
- ข้อผิดพลาดขั้นต้น
- ข้อผิดพลาดแบบสุ่ม
- ข้อผิดพลาดของระบบ
ตอนนี้ให้เราพูดคุยเกี่ยวกับข้อผิดพลาดในการวัดทั้งสามประเภทนี้ทีละประเภท
ข้อผิดพลาดขั้นต้น
ข้อผิดพลาดที่เกิดขึ้นเนื่องจากผู้สังเกตขาดประสบการณ์ในขณะที่รับค่าการวัดเรียกว่า gross errors. ค่าของข้อผิดพลาดขั้นต้นจะแตกต่างกันไปในแต่ละผู้สังเกตการณ์ บางครั้งข้อผิดพลาดขั้นต้นอาจเกิดขึ้นเนื่องจากการเลือกเครื่องมือที่ไม่เหมาะสม เราสามารถลดข้อผิดพลาดขั้นต้นได้โดยทำตามสองขั้นตอนนี้
- เลือกเครื่องมือที่เหมาะสมที่สุดโดยพิจารณาจากช่วงของค่าที่จะวัด
- จดบันทึกการอ่านอย่างละเอียด
ข้อผิดพลาดของระบบ
หากเครื่องมือก่อให้เกิดข้อผิดพลาดซึ่งมีค่าเบี่ยงเบนสม่ำเสมอสม่ำเสมอระหว่างการทำงานเรียกว่า systematic error. ข้อผิดพลาดอย่างเป็นระบบเกิดขึ้นเนื่องจากลักษณะของวัสดุที่ใช้ในเครื่องมือ
Types of Systematic Errors
ข้อผิดพลาดที่เป็นระบบสามารถแบ่งออกได้ดังต่อไปนี้ three types.
Instrumental Errors - ข้อผิดพลาดประเภทนี้เกิดขึ้นเนื่องจากข้อบกพร่องของเครื่องมือและผลกระทบในการโหลด
Environmental Errors - ข้อผิดพลาดประเภทนี้เกิดขึ้นเนื่องจากการเปลี่ยนแปลงของสภาพแวดล้อมเช่นการเปลี่ยนแปลงของอุณหภูมิความดันและอื่น ๆ
observational Errors - ข้อผิดพลาดประเภทนี้เกิดขึ้นเนื่องจากผู้สังเกตขณะอ่านค่ามิเตอร์ Parallax errors เป็นของข้อผิดพลาดประเภทนี้
ข้อผิดพลาดแบบสุ่ม
ข้อผิดพลาดซึ่งเกิดขึ้นเนื่องจากแหล่งที่มาที่ไม่รู้จักในช่วงเวลาการวัดเรียกว่า random errors. ดังนั้นจึงไม่สามารถกำจัดหรือลดข้อผิดพลาดเหล่านี้ได้ แต่ถ้าเราต้องการให้ได้ค่าการวัดที่แม่นยำยิ่งขึ้นโดยไม่มีข้อผิดพลาดแบบสุ่มก็สามารถทำได้โดยทำตามสองขั้นตอนนี้
Step1 - อ่านจำนวนมากขึ้นโดยผู้สังเกตการณ์ที่แตกต่างกัน
Step2 - ทำการวิเคราะห์ทางสถิติเกี่ยวกับการอ่านที่ได้รับในขั้นตอนที่ 1
ต่อไปนี้เป็นพารามิเตอร์ที่ใช้ในการวิเคราะห์ทางสถิติ
- Mean
- Median
- Variance
- Deviation
- ส่วนเบี่ยงเบนมาตรฐาน
ตอนนี้ให้เราพูดคุยเกี่ยวกับสิ่งเหล่านี้ statistical parameters.
ค่าเฉลี่ย
ให้ $ x_ {1}, x_ {2}, x_ {3}, .... , x_ {N} $ เป็นการอ่านค่า $ N $ ของการวัดหนึ่ง ๆ ค่าเฉลี่ยหรือaverage value การอ่านค่าเหล่านี้สามารถคำนวณได้โดยใช้สูตรต่อไปนี้
$$ m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N} $$
โดยที่ $ m $ คือค่าเฉลี่ยหรือค่าเฉลี่ย
หากจำนวนการอ่านค่าของการวัดเฉพาะมากกว่านั้นค่าเฉลี่ยหรือค่าเฉลี่ยจะเท่ากับโดยประมาณ true value
ค่ามัธยฐาน
หากจำนวนการอ่านค่าของการวัดเฉพาะมีมากขึ้นการคำนวณค่าเฉลี่ยหรือค่าเฉลี่ยนั้นเป็นเรื่องยาก ที่นี่คำนวณmedian value และจะมีค่าเท่ากับค่าเฉลี่ยโดยประมาณ
สำหรับการคำนวณค่ามัธยฐานก่อนอื่นเราต้องจัดเรียงการอ่านของการวัดเฉพาะในไฟล์ ascending order. เราสามารถคำนวณค่ามัธยฐานได้โดยใช้สูตรต่อไปนี้เมื่อจำนวนการอ่านเป็นodd number.
$$ M = x _ {\ left (\ frac {N + 1} {2} \ right)} $$
เราสามารถคำนวณค่ามัธยฐานได้โดยใช้สูตรต่อไปนี้เมื่อจำนวนการอ่านเป็น even number.
$$ M = \ frac {x _ {\ left (N / 2 \ right)} + x_ \ left (\ left [N / 2 \ right] +1 \ right)} {2} $$
ค่าเบี่ยงเบนจากค่าเฉลี่ย
ความแตกต่างระหว่างการอ่านของวัดโดยเฉพาะและค่าเฉลี่ยเป็นที่รู้จักกันการเบี่ยงเบนจากค่าเฉลี่ย ในระยะสั้นก็จะเรียกว่าเบี่ยงเบน ในทางคณิตศาสตร์สามารถแสดงเป็น
$$ d_ {i} = x_ {i} -m $$
ที่ไหน
$ d_ {i} $ คือส่วนเบี่ยงเบนของ $ i ^ {th} $ อ่านจากค่าเฉลี่ย
$ x_ {i} $ คือค่าของ $ i ^ {th} $ reading
$ m $ คือค่าเฉลี่ยหรือค่าเฉลี่ย
ส่วนเบี่ยงเบนมาตรฐาน
ค่าความเบี่ยงเบนของค่าเฉลี่ยรากถูกเรียกว่า standard deviation. ในทางคณิตศาสตร์สามารถแสดงเป็น
$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N}} $$
สูตรข้างต้นใช้ได้ถ้าจำนวนการอ่าน N มากกว่าหรือเท่ากับ 20 เราสามารถใช้สูตรต่อไปนี้สำหรับค่าเบี่ยงเบนมาตรฐานเมื่อจำนวนการอ่าน N น้อยกว่า 20
$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N-1}} $$
ที่ไหน
$ \ sigma $ คือค่าเบี่ยงเบนมาตรฐาน
$ d_ {1}, d_ {2}, d_ {3}, …, d_ {N} $ คือส่วนเบี่ยงเบนของการอ่านครั้งแรก, สอง, สาม, …, $ N ^ {th} $ จากค่าเฉลี่ยตามลำดับ
Note - ถ้าค่าเบี่ยงเบนมาตรฐานมีค่าน้อยการอ่านค่าของการวัดจะมีความแม่นยำมากขึ้น
ความแปรปรวน
กำลังสองของค่าเบี่ยงเบนมาตรฐานเรียกว่า variance. ในทางคณิตศาสตร์สามารถแสดงเป็น
$$ V = \ sigma ^ {2} $$
ที่ไหน
$ V $ คือความแปรปรวน
$ \ sigma $ คือค่าเบี่ยงเบนมาตรฐาน
เรียกอีกอย่างว่ากำลังสองเฉลี่ยของความเบี่ยงเบน variance. ในทางคณิตศาสตร์สามารถแสดงเป็น
$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N} $$
สูตรข้างต้นใช้ได้ถ้าจำนวนการอ่าน N มากกว่าหรือเท่ากับ 20 เราสามารถใช้สูตรต่อไปนี้สำหรับความแปรปรวนเมื่อจำนวนการอ่าน N น้อยกว่า 20
$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N-1} $$
ที่ไหน
$ V $ คือความแปรปรวน
$ d_ {1}, d_ {2}, d_ {3}, …, d_ {N} $ คือส่วนเบี่ยงเบนของการอ่านครั้งแรก, สอง, สาม, …, $ N ^ {th} $ จากค่าเฉลี่ยตามลำดับ
ดังนั้นด้วยความช่วยเหลือของพารามิเตอร์ทางสถิติเราสามารถวิเคราะห์การอ่านค่าของการวัดเฉพาะได้ ด้วยวิธีนี้เราจะได้ค่าการวัดที่แม่นยำยิ่งขึ้น
เครื่องมือที่ใช้ในการวัดปริมาณใด ๆ เรียกว่า measuring instruments. หากเครื่องมือสามารถวัดปริมาณไฟฟ้าพื้นฐานเช่นแรงดันและกระแสเรียกว่าbasic measuring instruments.
ประเภทของเครื่องมือวัดพื้นฐาน
เราสามารถแบ่งประเภทของเครื่องมือวัดพื้นฐานออกเป็นสองประเภทดังต่อไปนี้
- Voltmeters
- Ammeters
ให้เราพูดคุยเกี่ยวกับเครื่องมือวัดพื้นฐานทั้งสองนี้โดยย่อ
โวลต์มิเตอร์
ตามชื่อ voltmeterเป็นเครื่องมือวัดที่วัดแรงดันไฟฟ้าข้ามจุดสองจุดของวงจรไฟฟ้า หน่วยของแรงดันไฟฟ้าคือโวลต์และเครื่องมือวัดคือมิเตอร์ ดังนั้นคำว่า "โวลต์มิเตอร์" จึงได้มาจากการรวมสองคำเข้าด้วยกัน“volt” และ “meter”.
เราสามารถแบ่งประเภทของโวลต์มิเตอร์ได้ดังต่อไปนี้ two types ขึ้นอยู่กับประเภทของแรงดันไฟฟ้าที่สามารถวัดได้
- โวลต์มิเตอร์ DC
- โวลต์มิเตอร์ AC
DC โวลต์มิเตอร์
ตามชื่อที่แนะนำ DC โวลต์มิเตอร์จะวัดค่า DC voltageข้ามจุดสองจุดของวงจรไฟฟ้า โวลต์มิเตอร์ DC ที่ใช้งานได้จริงแสดงไว้ในรูปด้านล่าง

DC โวลต์มิเตอร์ที่แสดงในรูปคือ a $(0-10)V$ DC voltmeter. ดังนั้นจึงสามารถใช้วัดแรงดันไฟฟ้ากระแสตรงจากศูนย์โวลต์ถึง 10 โวลต์
โวลต์มิเตอร์ AC
ตามชื่อที่แนะนำโวลต์มิเตอร์ AC จะวัดค่า AC voltageข้ามจุดสองจุดของวงจรไฟฟ้า โวลต์มิเตอร์ AC ที่ใช้งานได้จริงแสดงไว้ในรูปด้านล่าง

โวลต์มิเตอร์ AC ที่แสดงในรูปด้านบนคือ a $(0-250)V$ AC voltmeter. ดังนั้นจึงสามารถใช้วัดแรงดันไฟฟ้ากระแสสลับจากศูนย์โวลต์ถึง 250 โวลต์
แอมมิเตอร์
ตามชื่อ ammeterเป็นเครื่องมือวัดที่ใช้วัดกระแสไฟฟ้าที่ไหลผ่านสองจุดของวงจรไฟฟ้า หน่วยของกระแสคือแอมแปร์และเครื่องมือวัดคือมิเตอร์ คำว่า "แอมมิเตอร์" ได้มาจากการรวมกัน“am” ของแอมแปร์ด้วย “meter”.
เราสามารถแบ่งประเภทของแอมป์มิเตอร์ได้ดังต่อไปนี้ two types ขึ้นอยู่กับประเภทของกระแสไฟฟ้าที่สามารถวัดได้
- แอมป์ DC
- แอมป์มิเตอร์ AC
DC แอมมิเตอร์
ตามชื่อที่แนะนำแอมป์มิเตอร์ DC จะวัดค่า DC currentที่ไหลผ่านจุดสองจุดของวงจรไฟฟ้า แอมป์มิเตอร์ DC ที่ใช้งานได้จริงแสดงในรูป

แอมป์มิเตอร์ DC ที่แสดงในรูปด้านบนคือ a $(0-50)A$ DC ammeter. ดังนั้นจึงสามารถใช้วัดกระแสไฟฟ้ากระแสตรงจากศูนย์แอมป์ถึง 50 แอมป์
แอมป์มิเตอร์ AC
ตามชื่อที่แนะนำแอมป์มิเตอร์ AC จะวัดค่า AC currentที่ไหลผ่านจุดสองจุดของวงจรไฟฟ้า แอมป์มิเตอร์ AC ที่ใช้งานได้จริงแสดงไว้ในรูปด้านล่าง

แอมป์มิเตอร์ AC ที่แสดงในรูปด้านบนคือ a $(0-100)A$ AC ammeter. ดังนั้นจึงสามารถใช้วัดกระแสไฟฟ้ากระแสสลับจากศูนย์แอมป์ถึง 100 แอมป์
เราจะพูดคุยเกี่ยวกับโวลต์มิเตอร์และแอมป์มิเตอร์ต่างๆโดยละเอียดในสองสามบทต่อไปนี้
DC โวลต์มิเตอร์เป็นเครื่องมือวัดซึ่งใช้ในการวัดแรงดันไฟฟ้ากระแสตรงในจุดใด ๆ ของวงจรไฟฟ้าสองจุด ถ้าเราวางตัวต้านทานแบบอนุกรมกับกัลวาโนมิเตอร์แบบขดลวดแม่เหล็กถาวร (PMMC) การรวมกันทั้งหมดจะทำหน้าที่เป็นDC voltmeter.
ความต้านทานแบบอนุกรมซึ่งใช้ในโวลต์มิเตอร์แบบ DC เรียกอีกอย่างว่าความต้านทานตัวคูณแบบอนุกรมหรือตัวคูณ โดยทั่วไปจะ จำกัด ปริมาณกระแสที่ไหลผ่านกัลวาโนมิเตอร์เพื่อป้องกันไม่ให้กระแสมิเตอร์เกินค่าการโก่งตัวเต็มสเกล circuit diagram ของโวลต์มิเตอร์ DC แสดงดังรูปด้านล่าง
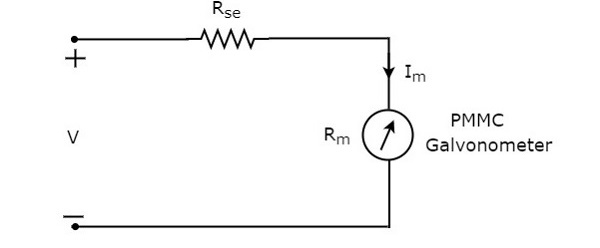
เราต้องวางโวลต์มิเตอร์ DC นี้ไว้ที่จุดสองจุดของวงจรไฟฟ้าซึ่งจะต้องวัดแรงดันไฟฟ้ากระแสตรง
สมัคร KVL รอบวงของวงจรด้านบน
$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (สมการ 1)
$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$
$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$
$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m} $ (สมการ 2)
ที่ไหน
$ R_ {se} $ คือความต้านทานของตัวคูณแบบอนุกรม
$ V $ คือแรงดันไฟฟ้ากระแสตรงแบบเต็มช่วงที่จะวัด
$ I_ {m} $ คือกระแสเบี่ยงเบนเต็มสเกล
$ R_ {m} $ คือความต้านทานภายในของกัลวาโนมิเตอร์
อัตราส่วนของแรงดันไฟฟ้ากระแสตรงแบบเต็มช่วงที่จะวัด $ V $ และแรงดันไฟฟ้ากระแสตรงตกคร่อมกัลวาโนมิเตอร์ $ V_ {m} $ เรียกว่า multiplying factor, ม. ในทางคณิตศาสตร์สามารถแสดงเป็น
$ m = \ frac {V} {V_ {m}} $ (สมการ 3)
จากสมการ 1 เราจะได้สมการต่อไปนี้สำหรับ full range DC voltage ที่จะวัดได้ $ V $
$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (สมการ 4)
DC voltage dropทั่วกัลวาโนมิเตอร์ $ V_ {m} $ คือผลคูณของกระแสโก่งเต็มสเกล $ I_ {m} $ และความต้านทานภายในของกัลวาโนมิเตอร์ $ R_ {m} $ ในทางคณิตศาสตร์สามารถเขียนเป็น
$ V_ {m} = I_ {m} R_ {m} $ (สมการ 5)
Substitute, สมการ 4 และสมการ 5 ในสมการ 3.
$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$
$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $
$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $
$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (สมการ 6)
เราสามารถค้นหาไฟล์ value of series multiplier resistance โดยใช้สมการ 2 หรือสมการ 6 ตามข้อมูลที่มี
โวลต์มิเตอร์ DC หลายช่วง
ในส่วนก่อนหน้านี้เราได้กล่าวถึงโวลต์มิเตอร์ DC ซึ่งได้มาจากการวางตัวต้านทานตัวคูณในอนุกรมกับกัลวาโนมิเตอร์ PMMC DC โวลต์มิเตอร์นี้สามารถใช้ในการวัด aparticular range ของแรงดันไฟฟ้ากระแสตรง
ถ้าเราต้องการใช้ DC โวลต์มิเตอร์สำหรับวัดแรงดันไฟฟ้ากระแสตรงของ multiple rangesจากนั้นเราต้องใช้ตัวต้านทานตัวคูณแบบขนานหลายตัวแทนตัวต้านทานตัวคูณเดี่ยวและการรวมกันของตัวต้านทานทั้งหมดนี้อยู่ในอนุกรมกับกัลวาโนมิเตอร์ PMMC circuit diagram ของโวลต์มิเตอร์ DC หลายช่วงแสดงไว้ในรูปด้านล่าง
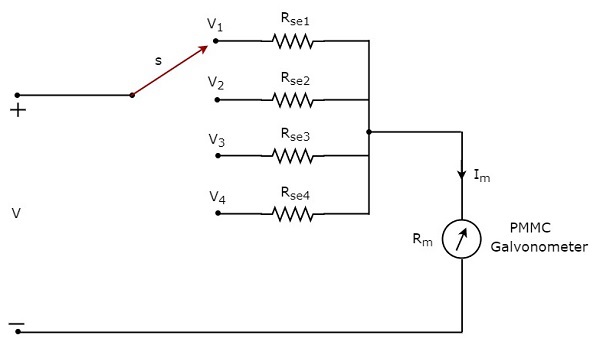
เราต้องวางสิ่งนี้ multi range DC voltmeterในจุดสองจุดของวงจรไฟฟ้าซึ่งจะต้องวัดแรงดันไฟฟ้ากระแสตรงของช่วงที่ต้องการ เราสามารถเลือกช่วงแรงดันไฟฟ้าที่ต้องการได้โดยเชื่อมต่อสวิตช์ s เข้ากับตัวต้านทานตัวคูณตามลำดับ
ให้ $ m_ {1}, m_ {2}, m_ {2} $ และ $ m_ {4} $ เป็น multiplying factorsของโวลต์มิเตอร์ DC เมื่อเราพิจารณาแรงดันไฟฟ้ากระแสตรงแบบเต็มช่วงที่จะวัดเป็น $ V_ {1} V_ {2} V_ {3} $ และ $ V_ {4} $ ตามลำดับ ต่อไปนี้เป็นสูตรที่สอดคล้องกับตัวคูณแต่ละตัว
$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$
$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$
$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$
$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$
ในวงจรด้านบนมีสี่ตัว series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ และ $ R_ {se4} $ ต่อไปนี้เป็นสูตรที่สอดคล้องกับตัวต้านทานทั้งสี่นี้
$$ R_ {se1} = R_ {m} \ left (m_ {1} -1 \ right) $$
$$ R_ {se2} = R_ {m} \ left (m_ {2} -1 \ right) $$
$$ R_ {se3} = R_ {m} \ left (m_ {3} -1 \ right) $$
$$ R_ {se4} = R_ {m} \ left (m_ {4} -1 \ right) $$
ดังนั้นเราสามารถค้นหาค่าความต้านทานของตัวต้านทานตัวคูณแต่ละชุดได้โดยใช้สูตรข้างต้น
เรียกว่าเครื่องมือที่ใช้วัดแรงดันไฟฟ้ากระแสสลับในสองจุดของวงจรไฟฟ้า AC voltmeter. หากโวลต์มิเตอร์ AC ประกอบด้วยวงจรเรียงกระแสแสดงว่าเป็นโวลต์มิเตอร์ AC ที่ใช้วงจรเรียงกระแส
โวลต์มิเตอร์ DC วัดเฉพาะแรงดันไฟฟ้ากระแสตรง หากเราต้องการใช้สำหรับวัดแรงดันไฟฟ้ากระแสสลับเราต้องทำตามสองขั้นตอนนี้
Step1 - แปลงสัญญาณแรงดันไฟฟ้ากระแสสลับเป็นสัญญาณแรงดันไฟฟ้ากระแสตรงโดยใช้วงจรเรียงกระแส
Step2 - วัด DC หรือค่าเฉลี่ยของสัญญาณเอาต์พุตของวงจรเรียงกระแส
เราได้รับ Rectifier based AC voltmeterเพียงแค่รวมวงจรเรียงกระแสเข้ากับโวลต์มิเตอร์ DC พื้นฐาน บทนี้เกี่ยวกับโวลต์มิเตอร์ AC ที่ใช้วงจรเรียงกระแส
ประเภทของโวลต์มิเตอร์ AC ที่ใช้วงจรเรียงกระแส
ต่อไปนี้คือไฟล์ two types ของโวลต์มิเตอร์ AC ที่ใช้วงจรเรียงกระแส
- โวลต์มิเตอร์ AC โดยใช้ Half Wave Rectifier
- โวลต์มิเตอร์ AC โดยใช้ Full Wave Rectifier
ตอนนี้ให้เราพูดคุยเกี่ยวกับโวลต์มิเตอร์ AC สองตัวนี้ทีละตัว
AC Voltmeter โดยใช้ Half Wave Rectifier
หากมีการเชื่อมต่อวงจรเรียงกระแสแบบ Half wave ก่อน DC โวลต์มิเตอร์การรวมกันทั้งหมดเข้าด้วยกันเรียกว่าโวลต์มิเตอร์ AC โดยใช้วงจรเรียงกระแสครึ่งคลื่น block diagram ของโวลต์มิเตอร์ AC โดยใช้วงจรเรียงกระแสครึ่งคลื่นแสดงดังรูปด้านล่าง
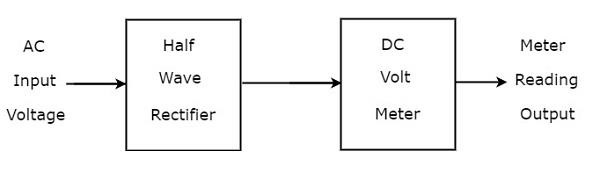
แผนภาพบล็อกด้านบนประกอบด้วยสองช่วงตึก: วงจรเรียงกระแสครึ่งคลื่นและโวลต์มิเตอร์ DC เราจะได้แผนภาพวงจรที่เกี่ยวข้องเพียงแค่แทนที่แต่ละบล็อกด้วยส่วนประกอบตามลำดับในแผนภาพบล็อกด้านบน ดังนั้นcircuit diagram ของโวลต์มิเตอร์ AC โดยใช้ Half wave rectifier จะมีลักษณะดังแสดงในรูปด้านล่าง
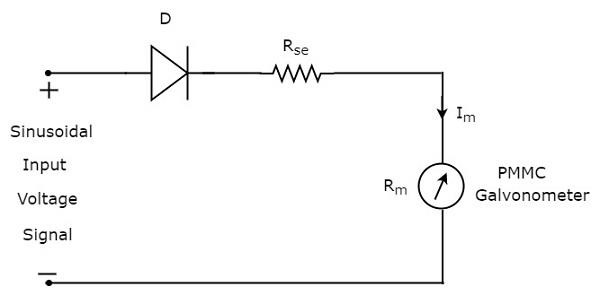
rms value ของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC) คือ
$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$
$$ \ Rightarrow V_ {m} = \ sqrt {2} V_ {rms} $$
$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$
ที่ไหน
$ V_ {m} $ คือค่าสูงสุดของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC)
DC หรือค่าเฉลี่ยของสัญญาณเอาต์พุตของ Half wave rectifier คือ
$$ V_ {dc} = \ frac {V_ {m}} {\ pi} $$
Substituteค่า $ V_ {m} $ ในสมการข้างบน
$$ V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi} $$
$$ V_ {dc} = 0.45 V_ {rms} $$
ดังนั้นโวลต์มิเตอร์ AC จึงสร้างแรงดันไฟฟ้าขาออกซึ่งเท่ากับ 0.45 คูณค่า rms ของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC)
AC Voltmeter โดยใช้ Full Wave Rectifier
หากเชื่อมต่อวงจรเรียงกระแสแบบเต็มคลื่นก่อน DC โวลต์มิเตอร์การรวมกันทั้งหมดเข้าด้วยกันเรียกว่าโวลต์มิเตอร์ AC โดยใช้วงจรเรียงกระแสแบบเต็มคลื่น block diagram ของโวลต์มิเตอร์ AC โดยใช้วงจรเรียงกระแสแบบเต็มคลื่นแสดงดังรูปด้านล่าง
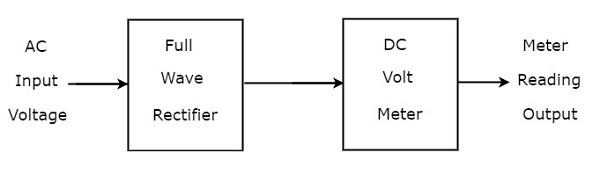
แผนภาพบล็อกด้านบนประกอบด้วยสองช่วงตึก: วงจรเรียงกระแสคลื่นเต็มและโวลต์มิเตอร์ DC เราจะได้แผนภาพวงจรที่เกี่ยวข้องเพียงแค่แทนที่แต่ละบล็อกด้วยส่วนประกอบตามลำดับในแผนภาพบล็อกด้านบน
ดังนั้น circuit diagram ของโวลต์มิเตอร์ AC โดยใช้ Full wave rectifier จะมีลักษณะดังแสดงในรูปด้านล่าง
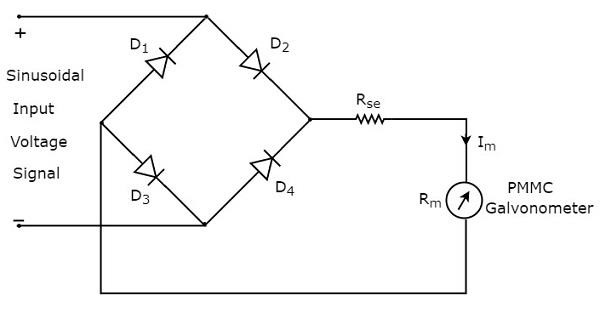
rms value ของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC) คือ
$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$
$$ \ Rightarrow V_ {m} = \ sqrt {2} \: V_ {rms} $$
$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$
ที่ไหน
$ V_ {m} $ คือค่าสูงสุดของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC)
DC หรือค่าเฉลี่ยของสัญญาณเอาต์พุตของ Full wave rectifier คือ
$$ V_ {dc} = \ frac {2V_ {m}} {\ pi} $$
Substituteค่า $ V_ {m} $ ในสมการข้างบน
$$ V_ {dc} = \ frac {2 \ times 1.414 \: V_ {rms}} {\ pi} $$
$$ V_ {dc} = 0.9 \: V_ {rms} $$
ดังนั้นโวลต์มิเตอร์ AC จึงสร้างแรงดันไฟฟ้าขาออกซึ่งเท่ากับ 0.9 คูณค่า rms ของสัญญาณแรงดันไฟฟ้าอินพุตไซน์ (AC)
ในบทที่แล้วเราได้พูดถึงเกี่ยวกับโวลต์มิเตอร์ AC ที่ใช้วงจรเรียงกระแส บทนี้ครอบคลุมโวลต์มิเตอร์ AC สองประเภทต่อไปนี้
- โวลต์มิเตอร์ AC ที่ตอบสนองสูงสุด
- True RMS ตอบสนองโวลต์มิเตอร์ AC
ตอนนี้ให้เราพูดคุยเกี่ยวกับโวลต์มิเตอร์ AC สองประเภทนี้ทีละประเภท
โวลต์มิเตอร์ AC ที่ตอบสนองสูงสุด
ตามชื่อที่แนะนำโวลต์มิเตอร์ AC ที่ตอบสนองสูงสุดจะตอบสนอง peak valuesของสัญญาณแรงดันไฟฟ้า AC นั่นหมายความว่าโวลต์มิเตอร์นี้จะวัดค่าสูงสุดของแรงดันไฟฟ้ากระแสสลับ circuit diagram ของโวลต์มิเตอร์ AC ที่ตอบสนองสูงสุดแสดงไว้ด้านล่าง -
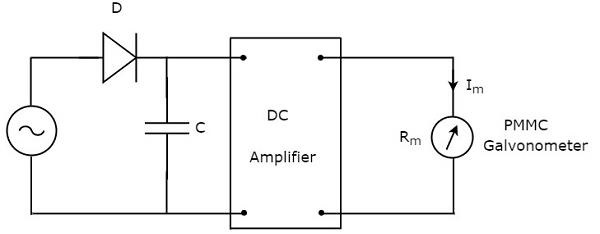
วงจรข้างต้นประกอบด้วยไดโอดตัวเก็บประจุเครื่องขยายเสียง DC และกัลวาโนมิเตอร์ PMMC ไดโอดที่มีอยู่ในวงจรข้างต้นใช้เพื่อวัตถุประสงค์ในการแก้ไข ดังนั้นไดโอดจะแปลงสัญญาณแรงดันไฟฟ้ากระแสสลับเป็นสัญญาณแรงดันไฟฟ้ากระแสตรง ตัวเก็บประจุจะชาร์จไปที่ค่าสูงสุดของสัญญาณแรงดันไฟฟ้ากระแสตรงนี้
ระหว่าง positive half cycleของสัญญาณแรงดันไฟฟ้ากระแสสลับไดโอดดำเนินการและตัวเก็บประจุจะชาร์จไปยังค่าสูงสุดของสัญญาณแรงดันไฟฟ้ากระแสสลับ เมื่อค่าของสัญญาณแรงดันไฟฟ้ากระแสสลับน้อยกว่าค่านี้ไดโอดจะเอนเอียงแบบย้อนกลับ
ดังนั้นตัวเก็บประจุจะปล่อยผ่านตัวต้านทานของเครื่องขยายเสียง DC จนถึงครึ่งรอบบวกของสัญญาณแรงดันไฟฟ้ากระแสสลับถัดไป เมื่อค่าของสัญญาณแรงดันไฟฟ้ากระแสสลับมากกว่าแรงดันตัวเก็บประจุไดโอดจะดำเนินการและกระบวนการจะถูกทำซ้ำ
เราควรเลือกค่าส่วนประกอบในลักษณะที่ตัวเก็บประจุชาร์จเร็วและคายประจุช้า เป็นผลให้มิเตอร์ตอบสนองต่อแรงดันไฟฟ้าของตัวเก็บประจุนี้เสมอเช่นpeak value of AC voltage.
True RMS ตอบสนอง AC โวลต์มิเตอร์
ตามชื่อที่แนะนำโวลต์มิเตอร์ AC ที่ตอบสนอง RMS ที่แท้จริงจะตอบสนองต่อค่า RMS ที่แท้จริงของสัญญาณแรงดันไฟฟ้ากระแสสลับ โวลต์มิเตอร์นี้วัดค่า RMS ของแรงดันไฟฟ้ากระแสสลับ circuit diagram ของโวลต์มิเตอร์ AC ที่ตอบสนอง RMS จริงแสดงไว้ในรูปด้านล่าง
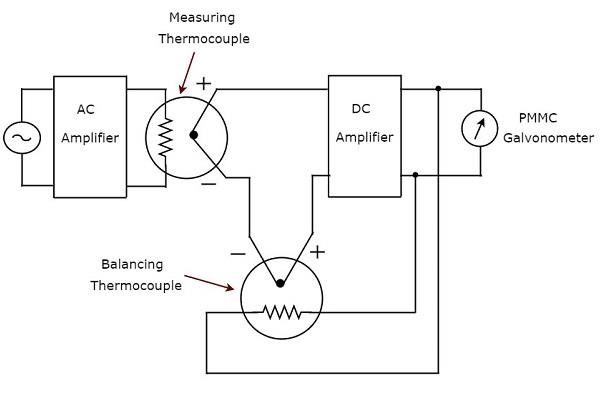
วงจรข้างต้นประกอบด้วยเครื่องขยายเสียง AC, เทอร์โมคัปเปิลสองตัว, เครื่องขยายเสียง DC และเครื่องวัดกระแสไฟฟ้า PMMC เครื่องขยายเสียง AC ขยายสัญญาณแรงดันไฟฟ้ากระแสสลับ เทอร์โมคัปเปิลสองตัวที่ใช้ในวงจรข้างต้นคือเทอร์โมคัปเปิลวัดและเทอร์โมคัปเปิลแบบปรับสมดุลMeasuring thermocouple สร้างแรงดันไฟฟ้าขาออกซึ่งเป็นสัดส่วนกับค่า RMS ของสัญญาณแรงดันไฟฟ้ากระแสสลับ
เทอร์โมคัปเปิลใด ๆ จะแปลงปริมาณอินพุตเป็นจำนวนปกติ ซึ่งหมายความว่ามีความสัมพันธ์แบบไม่เป็นเชิงเส้นระหว่างเอาต์พุตและอินพุตของเทอร์โมคัปเปิล ผลกระทบของพฤติกรรมที่ไม่เป็นเชิงเส้นของเทอร์โมคัปเปิลสามารถละเลยได้โดยใช้เทอร์โมคัปเปิลอื่นในวงจรป้อนกลับ เทอร์โมคัปเปิลที่ใช้เพื่อจุดประสงค์นี้ในวงจรข้างต้นเรียกว่าbalancing thermocouple.
เทอร์โมคัปเปิลสองตัวคือการวัดเทอร์โมคัปเปิลและการปรับสมดุลเทอร์โมคัปเปิลเข้าด้วยกันเป็นเจ้าสาวที่อินพุตของเครื่องขยายเสียง DC เป็นผลให้มิเตอร์ตอบสนองต่อtrue RMS value ของสัญญาณแรงดันไฟฟ้า AC
กระแสคืออัตราการไหลของประจุไฟฟ้า หากประจุไฟฟ้านี้ไหลไปในทิศทางเดียวกระแสไฟฟ้าที่เป็นผลลัพธ์จะเรียกว่ากระแสตรง (DC) เครื่องมือที่ใช้วัดกระแสตรงเรียกว่าDC ammeter.
ถ้าเราวางตัวต้านทานขนานกับกัลวาโนมิเตอร์แบบขดลวดแม่เหล็กถาวร (PMMC) ชุดค่าผสมทั้งหมดจะทำหน้าที่เป็นแอมป์มิเตอร์ DC ความต้านทานแบบขนานซึ่งใช้ใน DC แอมมิเตอร์เรียกอีกอย่างว่าความต้านทานแบบปัดหรือง่ายๆshunt. ควรพิจารณาค่าความต้านทานนี้ให้น้อยเพื่อวัดกระแสไฟฟ้ากระแสตรงที่มีค่ามาก
circuit diagram ของแอมป์มิเตอร์ DC แสดงในรูปด้านล่าง
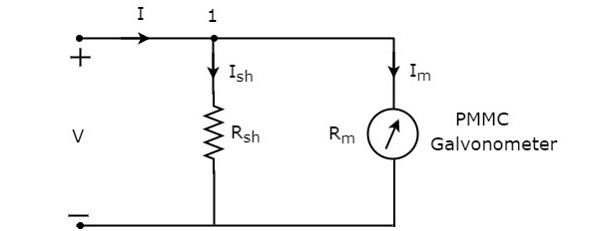
เราต้องวางสิ่งนี้ DC ammeterในอนุกรมกับสาขาของวงจรไฟฟ้าที่จะวัดกระแสไฟฟ้ากระแสตรง แรงดันไฟฟ้าคร่อมองค์ประกอบที่เชื่อมต่อแบบขนานจะเท่ากัน ดังนั้นแรงดันไฟฟ้าข้ามตัวต้านทานแบบแบ่ง $ R_ {sh} $ และแรงดันไฟฟ้าข้ามความต้านทานกระแสไฟฟ้า $ R_ {m} $ จึงเหมือนกันเนื่องจากองค์ประกอบทั้งสองนี้เชื่อมต่อแบบขนานในวงจรด้านบนMathematicallyสามารถเขียนเป็น
$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$
$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (สมการ 1)
KCL equation ที่โหนด 1 คือ
$$ - I + I_ {sh} + I_ {m} = 0 $$
$$ \ Rightarrow I_ {sh} = I-I_ {m} $$
Substitute ค่าของ $ I_ {sh} $ ในสมการ 1
$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (สมการ 2)
ใช้ $ I_ {m} $ เหมือนกันในพจน์ตัวส่วนซึ่งอยู่ทางขวามือของสมการ 2
$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m} (\ frac {1} {I_ {m}} - 1)} $$
$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}} - 1} $ (สมการ 3)
ที่ไหน
$ R_ {sh} $ คือความต้านทานการปัด
$ R_ {m} $ คือความต้านทานภายในของกัลวาโนมิเตอร์
$ I $ คือกระแสตรงทั้งหมดที่จะวัดได้
$ I_ {m} $ คือกระแสเบี่ยงเบนเต็มสเกล
อัตราส่วนของกระแสตรงทั้งหมดที่จะวัดได้ $ I $ และกระแสเบี่ยงเบนเต็มสเกลของกัลวาโนมิเตอร์ $ I_ {m} $ เรียกว่า multiplying factor, m. ในทางคณิตศาสตร์สามารถแสดงเป็น
$ m = \ frac {I} {I_ {m}} $ (สมการ 4)
$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (สมการ 5)
เราสามารถค้นหาไฟล์ value of shunt resistance โดยใช้สมการ 2 หรือสมการ 5 ตามข้อมูลที่มี
แอมป์มิเตอร์ DC หลายช่วง
ในส่วนก่อนหน้านี้เราได้กล่าวถึงแอมป์มิเตอร์ DC ซึ่งได้จากการวางตัวต้านทานควบคู่ไปกับกัลวาโนมิเตอร์ PMMC แอมป์มิเตอร์ DC นี้สามารถใช้ในการวัด aparticular range ของกระแสตรง
หากเราต้องการใช้แอมป์มิเตอร์ DC สำหรับวัดกระแสตรงของ multiple rangesจากนั้นเราต้องใช้ตัวต้านทานแบบขนานหลายตัวแทนตัวต้านทานเดี่ยวและการรวมกันของตัวต้านทานทั้งหมดนี้จะขนานกับกัลวาโนมิเตอร์ PMMC circuit diagram ของแอมป์มิเตอร์ DC หลายช่วงแสดงไว้ในรูปด้านล่าง
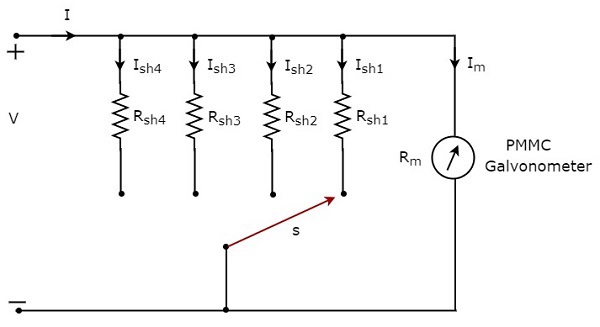
วางแอมป์มิเตอร์ DC แบบหลายช่วงเป็นอนุกรมพร้อมกับสาขาของวงจรไฟฟ้าซึ่งจะวัดกระแสตรงของช่วงที่ต้องการ ช่วงของกระแสที่ต้องการถูกเลือกโดยการเชื่อมต่อสวิตช์ s กับตัวต้านทานแบบแบ่งตามลำดับ
ให้ $ m_ {1}, m_ {2}, m_ {3} $ และ $ m_ {4} $ เป็น multiplying factorsของแอมป์มิเตอร์ DC เมื่อเราพิจารณากระแสตรงทั้งหมดที่จะวัดเป็น $ I_ {1} I_ {2} I_ {3} $ และ $ I_ {4} $ ตามลำดับ ต่อไปนี้เป็นสูตรที่สอดคล้องกับตัวคูณแต่ละตัว
$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$
$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$
$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$
$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$
ในวงจรด้านบนมีสี่ตัว shunt resistors, $ R_ {sh1}, R_ {sh2}, R_ {sh2} $ และ $ R_ {sh4} $ ต่อไปนี้เป็นสูตรที่สอดคล้องกับตัวต้านทานทั้งสี่นี้
$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$
$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$
$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$
$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$
สูตรข้างต้นจะช่วยให้เราค้นหาค่าความต้านทานของตัวต้านทานแต่ละตัว
กระแสคืออัตราการไหลของประจุไฟฟ้า หากทิศทางของประจุไฟฟ้านี้เปลี่ยนไปอย่างสม่ำเสมอกระแสไฟฟ้าที่เป็นผลลัพธ์จะถูกเรียกว่าAlternating Current (AC).
เรียกว่าเครื่องมือที่ใช้วัดกระแสสลับที่ไหลผ่านสาขาใด ๆ ของวงจรไฟฟ้า AC ammeter.
Example - แอมป์มิเตอร์ AC ชนิดเทอร์โมคัปเปิล
ตอนนี้ให้เราพูดคุยเกี่ยวกับแอมป์มิเตอร์ AC ชนิดเทอร์โมคัปเปิล
แอมมิเตอร์ AC ชนิดเทอร์โมคัปเปิล
หากเชื่อมต่อเทอร์โมคัปเปิลก่อนเครื่องวัดกระแสไฟฟ้า PMMC ชุดค่าผสมทั้งหมดนี้เรียกว่าแอมป์มิเตอร์ AC ชนิดเทอร์โมคัปเปิล block diagram ของแอมป์มิเตอร์ AC ชนิดเทอร์โมคัปเปิลแสดงดังรูปด้านล่าง
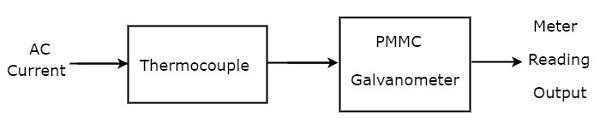
แผนภาพบล็อกด้านบนประกอบด้วยสองช่วงตึกส่วนใหญ่คือเทอร์โมคัปเปิลและกัลวาโนมิเตอร์ PMMC เราจะได้แผนภาพวงจรที่เกี่ยวข้องเพียงแค่แทนที่แต่ละบล็อกด้วยส่วนประกอบตามลำดับในแผนภาพบล็อกด้านบน ดังนั้นcircuit diagram ของแอมป์มิเตอร์ AC ชนิดเทอร์โมคัปเปิลจะมีลักษณะดังแสดงในรูปด้านล่าง
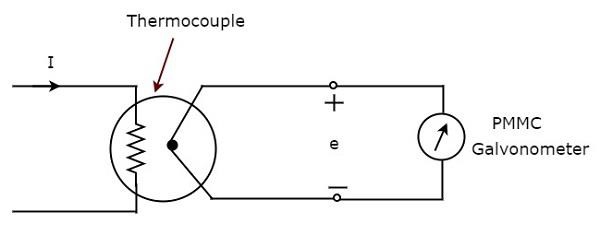
เทอร์โมคัปเปิลสร้าง EMF, $ e $ เมื่อใดก็ตามที่กระแสสลับฉันไหลผ่านองค์ประกอบฮีตเตอร์ EMF นี้ $ e $ แปรผันตรงกับค่า rms ของกระแส I ที่ไหลผ่านองค์ประกอบฮีตเตอร์ ดังนั้นเราต้องสอบเทียบมาตราส่วนของเครื่องมือ PMMC เพื่ออ่านrms values of current.
ดังนั้นในบทนี้เราได้ทำเครื่องมือวัดพื้นฐานทั้งหมดเช่นโวลต์มิเตอร์ DC โวลต์มิเตอร์ AC แอมป์มิเตอร์ DC และแอมป์มิเตอร์ AC ในบทถัดไปให้เราพูดคุยเกี่ยวกับมิเตอร์หรือเครื่องมือวัดซึ่งใช้วัดค่าความต้านทาน
เครื่องมือที่ใช้วัดค่าความต้านทานระหว่างจุดสองจุดในวงจรไฟฟ้าเรียกว่า ohmmeter. นอกจากนี้ยังสามารถใช้เพื่อหาค่าของตัวต้านทานที่ไม่รู้จัก หน่วยของความต้านทานคือโอห์มและเครื่องมือวัดคือมิเตอร์ ดังนั้นคำว่า "โอห์มมิเตอร์" จึงได้มาจากการรวมคำ“ohm” และ “meter”.
ประเภทของโอห์มมิเตอร์
ต่อไปนี้คือไฟล์ two types ของโอห์มมิเตอร์
- ซีรีส์โอห์มมิเตอร์
- ปัดโอห์มมิเตอร์
ตอนนี้ให้เราพูดคุยเกี่ยวกับโอห์มมิเตอร์สองประเภทนี้ทีละประเภท
ซีรีส์โอห์มมิเตอร์
หากไม่ทราบค่าของตัวต้านทานและจะต้องวัดโดยวางเป็นอนุกรมกับโอห์มมิเตอร์โอห์มมิเตอร์นั้นเรียกว่าโอห์มมิเตอร์แบบอนุกรม circuit diagram ของโอห์มมิเตอร์แบบอนุกรมแสดงไว้ในรูปด้านล่าง
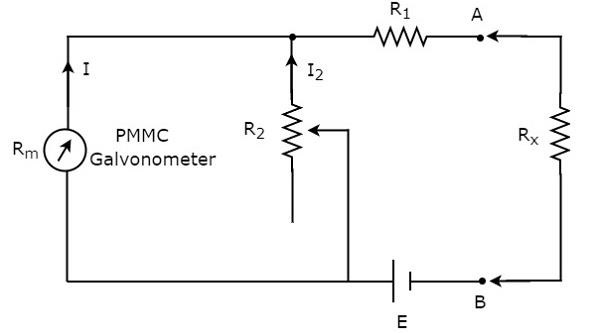
ส่วนของวงจรซึ่งอยู่ด้านซ้ายของขั้ว A & B คือ series ohmmeter. ดังนั้นเราสามารถวัดค่าของความต้านทานที่ไม่รู้จักได้โดยวางไว้ทางด้านขวาของขั้ว A & B ตอนนี้ให้เราคุยเกี่ยวกับcalibration scale ของโอห์มมิเตอร์แบบอนุกรม
ถ้า $ R_ {x} = 0 \: \ Omega $ ขั้ว A & B จะลัดวงจรซึ่งกันและกัน ดังนั้นกระแสมิเตอร์จะถูกหารระหว่างตัวต้านทาน $ R_ {1} $ และ $ R_ {2} $ ตอนนี้เปลี่ยนค่าของตัวต้านทาน $ R_ {2} $ ในลักษณะที่กระแสมิเตอร์ทั้งหมดไหลผ่านตัวต้านทาน $ R_ {1} $ เท่านั้น ในกรณีนี้มิเตอร์จะแสดงเต็มscale deflection current. ดังนั้นกระแสการเบี่ยงเบนเต็มสเกลของมิเตอร์จึงแสดงเป็น $ 0 \: \ Omega $
ถ้า $ R_ {x} = \ infty \: \ Omega $ ดังนั้นเทอร์มินัล A & B จะเปิดเวียนเข้าหากัน ดังนั้นจึงไม่มีกระแสไหลผ่านตัวต้านทาน $ R_ {1} $ ในกรณีนี้มิเตอร์จะแสดงกระแสเบี่ยงเบนเป็นโมฆะ ดังนั้นการโก่งตัวเป็นโมฆะของมิเตอร์จึงสามารถแสดงเป็น $ \ infty \ Omega $
ด้วยวิธีนี้เมื่อพิจารณาค่าที่แตกต่างกันของ $ R_ {x} $ มิเตอร์จะแสดงการเบี่ยงเบนที่แตกต่างกัน ดังนั้นเราจึงสามารถแสดงการเบี่ยงเบนเหล่านั้นด้วยค่าความต้านทานที่สอดคล้องกัน
โอห์มมิเตอร์แบบอนุกรมประกอบด้วยมาตราส่วนการสอบเทียบ มีสัญลักษณ์เป็น 0 $ \ Omega $ และ $ \ infty \: \ Omega $ ที่จุดสิ้นสุดของมือขวาและมือซ้ายของเครื่องชั่งตามลำดับ ซีรีส์โอห์มมิเตอร์มีประโยชน์ในการวัดhigh values of resistances.
ปัดโอห์มมิเตอร์
หากไม่ทราบค่าของตัวต้านทานและจะวัดโดยวางขนาน (shunt) กับโอห์มมิเตอร์โอห์มมิเตอร์นั้นเรียกว่า shunt ohmmeter circuit diagram ของโอห์มมิเตอร์ปัดแสดงในรูปด้านล่าง
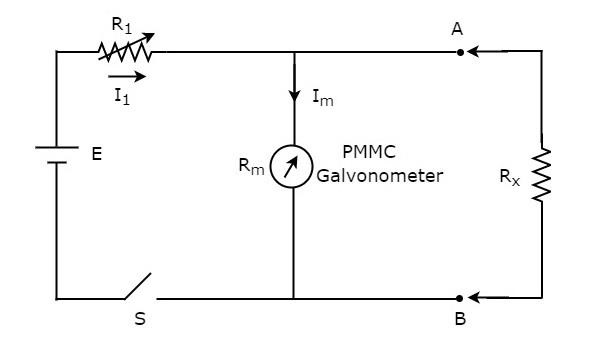
ส่วนของวงจรซึ่งอยู่ด้านซ้ายของขั้ว A & B คือ shunt ohmmeter. ดังนั้นเราสามารถวัดค่าของความต้านทานที่ไม่รู้จักได้โดยวางไว้ทางด้านขวาของขั้ว A & B
ตอนนี้ให้เราพูดคุยเกี่ยวกับ calibration scaleของโอห์มมิเตอร์ปัด ปิดสวิตช์ S ของวงจรด้านบนขณะใช้งาน
ถ้า $ R_ {x} = 0 \: \ Omega $ ขั้ว A & B จะลัดวงจรซึ่งกันและกัน ด้วยเหตุนี้กระแสไฟฟ้าทั้งหมด $ I_ {1} $ จึงไหลผ่านขั้ว A & B ในกรณีนี้ไม่มีกระแสไฟฟ้าไหลผ่านเครื่องวัดกระแสไฟฟ้า PMMC ดังนั้นnull deflection ของเครื่องวัดกระแสไฟฟ้า PMMC สามารถแสดงเป็น $ 0 \: \ Omega $
ถ้า $ R_ {x} = \ infty \: \ Omega $ ดังนั้นเทอร์มินัล A & B จะเปิดเวียนเข้าหากัน ดังนั้นจึงไม่มีกระแสไหลผ่านขั้ว A & B ในกรณีนี้กระแสไฟฟ้าทั้งหมด $ I_ {1} $ ไหลผ่านเครื่องวัดกระแสไฟฟ้า PMMC หากต้องการเปลี่ยนแปลง (ปรับ) ค่าของตัวต้านทาน $ R_ {1} $ จนกว่ากัลวาโนมิเตอร์ PMMC จะแสดงกระแสโก่งเต็มสเกล ดังนั้นสิ่งนี้full scale deflection กระแสของเครื่องวัดกระแสไฟฟ้า PMMC สามารถแสดงเป็น $ \ infty \: \ Omega $
ด้วยวิธีนี้เมื่อพิจารณาค่าที่แตกต่างกันของ $ R_ {x} $ มิเตอร์จะแสดงการเบี่ยงเบนที่แตกต่างกัน ดังนั้นเราจึงสามารถแสดงการเบี่ยงเบนเหล่านั้นด้วยค่าความต้านทานที่สอดคล้องกัน
โอห์มมิเตอร์ shunt ประกอบด้วยมาตราส่วนการสอบเทียบ มีข้อบ่งชี้เป็น $ 0 \: \ Omega $ และ $ \ infty \: \ Omega $ ที่จุดสิ้นสุดของมือซ้ายและขวาของเครื่องชั่งตามลำดับ
Shunt ohmmeter มีประโยชน์ในการวัด low values of resistances. ดังนั้นเราสามารถใช้โอห์มมิเตอร์แบบอนุกรมหรือโอห์มมิเตอร์ปัดตามค่าของความต้านทานที่จะวัดได้เช่นสูงหรือต่ำ
ในบทก่อนหน้านี้เราได้กล่าวถึงโวลต์มิเตอร์แอมป์มิเตอร์และโอห์มมิเตอร์ เครื่องมือวัดเหล่านี้ใช้ในการวัดแรงดันกระแสและความต้านทานตามลำดับ นั่นหมายความว่าเรามีseparate measuring instruments สำหรับการวัดแรงดันกระแสและความต้านทาน
สมมติว่าหากสามารถใช้เครื่องมือวัดตัวเดียวเพื่อวัดปริมาณเช่นแรงดันกระแสและความต้านทานทีละครั้งก็จะกล่าวได้ว่าเป็น multimeter. มันมีชื่อมัลติมิเตอร์เนื่องจากสามารถวัดปริมาณไฟฟ้าได้ทีละหลาย ๆ
การวัดโดยใช้มัลติมิเตอร์
Multimeterเป็นเครื่องมือที่ใช้ในการวัดแรงดันไฟฟ้ากระแสตรงและกระแสสลับกระแสไฟฟ้ากระแสตรงและกระแสสลับและความต้านทานหลายช่วง เรียกอีกอย่างว่า Electronic Multimeter หรือ Voltage Ohm Meter (VOM)
การวัดแรงดันไฟฟ้ากระแสตรง
ส่วนของ circuit diagram ของมัลติมิเตอร์ที่สามารถใช้วัดแรงดันไฟฟ้ากระแสตรงได้ดังรูปด้านล่าง
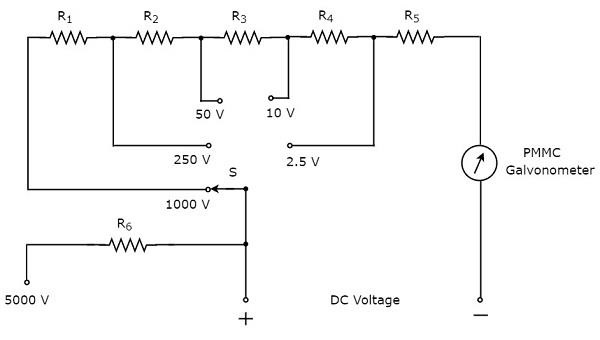
วงจรข้างต้นดูเหมือนโวลต์มิเตอร์ DC หลายช่วง การรวมกันของตัวต้านทานแบบอนุกรมกับกัลวาโนมิเตอร์ PMMC คือDC voltmeter. ดังนั้นจึงสามารถใช้วัดแรงดันไฟฟ้ากระแสตรงได้ถึงค่าที่แน่นอน
เราสามารถเพิ่มช่วงของแรงดันไฟฟ้ากระแสตรงที่วัดได้ด้วย DC โวลต์มิเตอร์เดียวกันโดยการเพิ่มค่าความต้านทาน ค่าความต้านทานเทียบเท่าจะเพิ่มขึ้นเมื่อเราเชื่อมต่อตัวต้านทานอยู่ในseries.
ในวงจรด้านบนเราสามารถวัดแรงดันไฟฟ้ากระแสตรงได้ถึง 2.5Vโดยใช้การรวมกันของตัวต้านทาน $ R_ {5} $ ในซีรีส์กับ PMMC กัลวาโนมิเตอร์ ด้วยการเชื่อมต่อตัวต้านทาน $ R_ {4} $ ในอนุกรมกับวงจรก่อนหน้าเราสามารถวัดแรงดันไฟฟ้ากระแสตรงได้ถึง10V. ด้วยวิธีนี้เราสามารถเพิ่มช่วงของแรงดันไฟฟ้ากระแสตรงได้เพียงแค่เชื่อมต่อตัวต้านทานแบบอนุกรมกับวงจรก่อนหน้า (ก่อนหน้า)
เราสามารถวัดแรงดันไฟฟ้ากระแสตรงในจุดใด ๆ สองจุดของวงจรไฟฟ้าโดยเชื่อมต่อสวิตช์ S กับช่วงแรงดันไฟฟ้าที่ต้องการ
การวัดกระแสไฟฟ้ากระแสตรง
ส่วนของ circuit diagram ของมัลติมิเตอร์ซึ่งสามารถใช้วัดกระแสไฟฟ้ากระแสตรงได้ดังรูปด้านล่าง
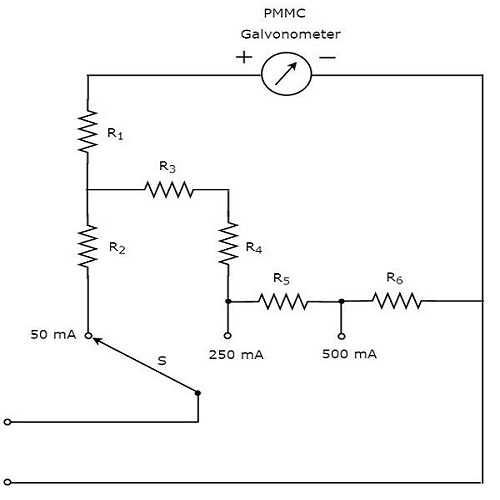
วงจรข้างต้นดูเหมือนแอมป์มิเตอร์ DC หลายช่วง การรวมกันของตัวต้านทานควบคู่ไปกับกัลวาโนมิเตอร์ PMMC คือDC ammeter. ดังนั้นจึงสามารถใช้วัดกระแสไฟฟ้ากระแสตรงได้ถึงค่าที่แน่นอน
เราจะได้รับ different rangesของกระแส DC ที่วัดด้วยแอมป์มิเตอร์ DC เดียวกันโดยวางตัวต้านทานขนานกับตัวต้านทานก่อนหน้า ในวงจรด้านบนตัวต้านทาน $ R_ {1} $ เชื่อมต่อแบบอนุกรมกับกัลวาโนมิเตอร์ PMMC เพื่อป้องกันมิเตอร์เสียหายเนื่องจากกระแสไฟฟ้ามาก
เราสามารถวัดกระแสไฟฟ้ากระแสตรงที่ไหลผ่านสองจุดของวงจรไฟฟ้าโดยเชื่อมต่อสวิตช์ S กับช่วงกระแสที่ต้องการ
การวัดแรงดันไฟฟ้ากระแสสลับ
ส่วนของ circuit diagram ของมัลติมิเตอร์ซึ่งสามารถใช้วัดแรงดันไฟฟ้ากระแสสลับได้ดังรูปด้านล่าง

วงจรข้างต้นดูเหมือน multi range AC voltmeter. เรารู้ว่าเราจะได้รับ AC โวลต์มิเตอร์เพียงแค่วางวงจรเรียงกระแสในอนุกรม (น้ำตก) ด้วยโวลต์มิเตอร์ DC วงจรข้างต้นถูกสร้างขึ้นโดยการวางชุดค่าผสมของไดโอดและตัวต้านทาน $ R_ {6} $ ไว้ระหว่างตัวต้านทาน, $ R_ {5} $ และเครื่องวัดกระแสไฟฟ้า PMMC
เราสามารถวัดแรงดันไฟฟ้ากระแสสลับในสองจุดใด ๆ ของวงจรไฟฟ้าโดยเชื่อมต่อสวิตช์ S กับช่วงแรงดันไฟฟ้าที่ต้องการ
การวัดความต้านทาน
ส่วนของ circuit diagram ของมัลติมิเตอร์ที่สามารถใช้วัดความต้านทานได้แสดงดังรูปด้านล่าง
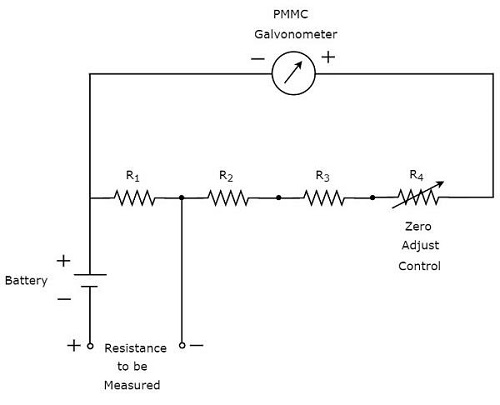
เราต้องทำงานสองอย่างต่อไปนี้ก่อนที่จะทำการวัดผลใด ๆ
- ลัดวงจรของเครื่องมือ
- เปลี่ยนการควบคุมการปรับค่าศูนย์จนกว่ามิเตอร์จะแสดงกระแสเต็มสเกล นั่นหมายความว่ามิเตอร์ระบุค่าความต้านทานเป็นศูนย์
ตอนนี้พฤติกรรมของวงจรดังกล่าวข้างต้นเป็นโอห์มมิเตอร์ปัดและมีคูณมาตราส่วน 1 คือ 10 0 นอกจากนี้เรายังสามารถพิจารณาอำนาจการสั่งซื้อที่สูงขึ้นของ 10 เป็นการคูณมาตราส่วนสำหรับการวัดค่าความต้านทานสูง
Signal generator เป็นอุปกรณ์อิเล็กทรอนิกส์ที่ให้สัญญาณทดสอบมาตรฐานเช่นคลื่นไซน์คลื่นสี่เหลี่ยมคลื่นสามเหลี่ยมและอื่น ๆ เรียกอีกอย่างว่าออสซิลเลเตอร์เนื่องจากสร้างสัญญาณเป็นระยะ
เครื่องกำเนิดสัญญาณซึ่งสร้างสัญญาณเป็นระยะที่มีความถี่ของช่วงความถี่เสียง (AF) เรียกว่า AF signal generator. ช่วงความถี่เสียงคือ 20Hz ถึง 20KHz
AF Sine และ Square Wave Generator
เครื่องกำเนิดสัญญาณ AF ซึ่งสร้างคลื่นไซน์หรือคลื่นสี่เหลี่ยมในช่วงความถี่เสียงตามความต้องการเรียกว่าเครื่องกำเนิดคลื่น AF Sine และ Square มันblock diagramดังแสดงในรูปด้านล่าง
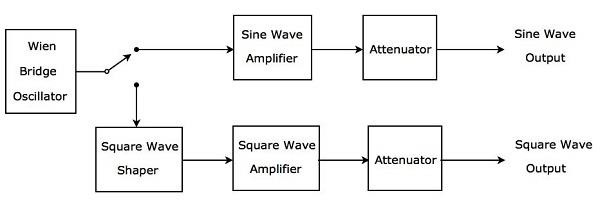
แผนภาพข้างต้นประกอบด้วยส่วนใหญ่ two paths. สิ่งเหล่านี้คือเส้นทางบนและเส้นทางล่าง เส้นทางด้านบนใช้ในการสร้างคลื่นไซน์ AF และทางเดินด้านล่างใช้ในการสร้างคลื่นสี่เหลี่ยม AF
Wien bridge oscillatorจะสร้างคลื่นไซน์ในช่วงความถี่เสียง ตามข้อกำหนดเราสามารถเชื่อมต่อเอาต์พุตของ Wien bridge oscillator กับเส้นทางบนหรือเส้นทางล่างโดยใช้สวิตช์
เส้นทางด้านบนประกอบด้วยบล็อกเช่นเครื่องขยายคลื่นไซน์และตัวลดทอนสัญญาณ หากใช้สวิตช์เพื่อเชื่อมต่อเอาท์พุทของ Wien bridge oscillator ไปยังพา ธ ด้านบนก็จะให้ผลลัพธ์ที่ต้องการAF sine wave ที่เอาต์พุตของเส้นทางด้านบน
เส้นทางด้านล่างประกอบด้วยบล็อกต่อไปนี้: ตัวปรับคลื่นสี่เหลี่ยม, แอมพลิฟายเออร์คลื่นสี่เหลี่ยมและตัวลดทอน เครื่องปรับคลื่นรูปสี่เหลี่ยมจะแปลงคลื่นไซน์เป็นคลื่นสี่เหลี่ยม หากใช้สวิตช์เพื่อเชื่อมต่อเอาท์พุทของ Wien bridge oscillator กับทางเดินที่ต่ำกว่าก็จะให้ผลลัพธ์ที่ต้องการAF square waveที่เอาต์พุตของเส้นทางด้านล่าง ด้วยวิธีนี้แผนภาพบล็อกที่เราพิจารณาสามารถใช้ในการสร้างคลื่นไซน์ AF หรือคลื่นสี่เหลี่ยม AF ตามข้อกำหนด
ฟังก์ชัน Generator
ฟังก์ชั่นเจเนอเรเตอร์เป็นเครื่องกำเนิดสัญญาณซึ่งสร้างคลื่นเป็นระยะตั้งแต่สามคลื่นขึ้นไป พิจารณาสิ่งต่อไปนี้block diagram ของเครื่องกำเนิดฟังก์ชันซึ่งจะสร้างคลื่นเป็นระยะเช่นคลื่นสามเหลี่ยมคลื่นสี่เหลี่ยมและคลื่นไซน์
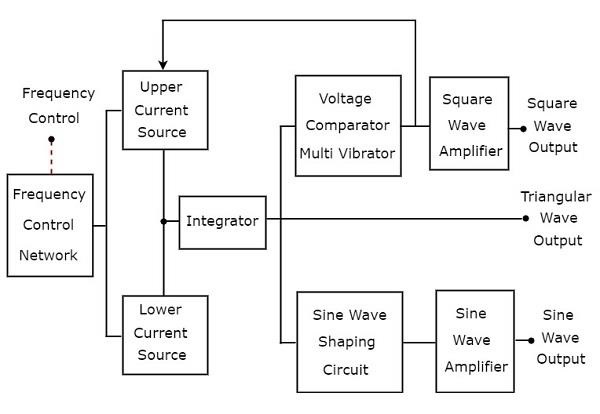
มีสอง current sourcesกล่าวคือแหล่งกระแสบนและแหล่งกระแสล่างในแผนภาพบล็อกด้านบน แหล่งกระแสไฟฟ้าทั้งสองนี้ถูกควบคุมโดยแรงดันไฟฟ้าที่ควบคุมความถี่
คลื่นสามเหลี่ยม
Integratorอยู่ในแผนภาพบล็อกด้านบนรับกระแสคงที่สลับกันจากแหล่งกระแสบนและล่างเป็นระยะเวลาที่เท่ากันซ้ำ ๆ ดังนั้นอินทิเกรเตอร์จะสร้างเอาต์พุตสองประเภทในเวลาเดียวกันซ้ำ ๆ -
แรงดันขาออกของอินทิเกรเตอร์ increases linearly ตามเวลาสำหรับช่วงเวลาที่อินทิเกรเตอร์ได้รับกระแสจากแหล่งกระแสบน
แรงดันขาออกของอินทิเกรเตอร์ decreases linearly ตามเวลาสำหรับช่วงเวลาที่อินทิเกรเตอร์ได้รับกระแสจากแหล่งกระแสที่ต่ำกว่า
ด้วยวิธีนี้ตัวรวมที่อยู่ในแผนภาพบล็อกด้านบนจะสร้างไฟล์ triangular wave.
Square Wave และ Sine Wave
เอาท์พุทของอินทิเกรเตอร์คือคลื่นสามเหลี่ยมถูกนำไปใช้เป็นอินพุตให้กับบล็อกอื่นอีกสองบล็อกดังที่แสดงในแผนภาพด้านบนเพื่อให้ได้คลื่นสี่เหลี่ยมและคลื่นไซน์ตามลำดับ ให้เราพูดคุยเกี่ยวกับสองสิ่งนี้ทีละคน
สแควร์เวฟ
คลื่นสามเหลี่ยมมีความชันบวกและความชันเชิงลบสลับกันเป็นระยะเวลาเท่า ๆ กันซ้ำ ๆ ดังนั้นvoltage comparator multi vibrator ที่มีอยู่ในแผนภาพด้านบนจะสร้างผลลัพธ์สองประเภทต่อไปนี้สำหรับระยะเวลาที่เท่ากันซ้ำ ๆ
ค่าคงที่ประเภทหนึ่ง (higher) voltage ที่เอาท์พุทของเครื่องสั่นหลายตัวเปรียบเทียบแรงดันไฟฟ้าสำหรับช่วงเวลาที่เครื่องสั่นหลายตัวเปรียบเทียบแรงดันได้รับความชันเชิงบวกของคลื่นสามเหลี่ยม
ค่าคงที่อีกประเภทหนึ่ง (lower) voltage ที่เอาท์พุทของเครื่องสั่นหลายตัวเปรียบเทียบแรงดันไฟฟ้าสำหรับช่วงเวลาที่เครื่องสั่นหลายตัวเปรียบเทียบแรงดันได้รับความชันเชิงลบของคลื่นสามเหลี่ยม
เครื่องสั่นหลายตัวเปรียบเทียบแรงดันไฟฟ้าที่มีอยู่ในแผนภาพบล็อกด้านบนจะสร้าง a square wave. หากแอมพลิจูดของคลื่นสี่เหลี่ยมที่ผลิตที่เอาท์พุทของเครื่องสั่นหลายตัวเปรียบเทียบแรงดันไฟฟ้าไม่เพียงพอก็สามารถขยายเป็นค่าที่ต้องการได้โดยใช้เครื่องขยายคลื่นสี่เหลี่ยม
ไซน์เวฟ
sine wave shaping circuitจะสร้างเอาต์พุตคลื่นไซน์จากคลื่นอินพุตสามเหลี่ยม โดยพื้นฐานแล้ววงจรนี้ประกอบด้วยเครือข่ายความต้านทานไดโอด หากแอมพลิจูดของคลื่นไซน์ที่ผลิตที่เอาต์พุตของวงจรสร้างคลื่นไซน์ไม่เพียงพอก็สามารถขยายเป็นค่าที่ต้องการได้โดยใช้เครื่องขยายคลื่นไซน์
เครื่องมืออิเล็กทรอนิกส์ที่ใช้ในการวิเคราะห์คลื่นเรียกว่า wave analyzer. เรียกอีกอย่างว่าตัววิเคราะห์สัญญาณเนื่องจากสัญญาณและคลื่นสามารถใช้แทนกันได้บ่อยๆ
เราสามารถเป็นตัวแทนของไฟล์ periodic signal เป็นผลรวมของสองคำต่อไปนี้
- ส่วนประกอบ DC
- อนุกรมของฮาร์มอนิกไซน์
ดังนั้นการวิเคราะห์สัญญาณเป็นระยะคือการวิเคราะห์ส่วนประกอบฮาร์มอนิกส์ที่แสดงอยู่ในนั้น
เครื่องวิเคราะห์คลื่นพื้นฐาน
เครื่องวิเคราะห์คลื่นพื้นฐานส่วนใหญ่ประกอบด้วยสามช่วงตึก ได้แก่ เครื่องตรวจจับหลักวงจรเรียงกระแสคลื่นเต็มรูปแบบและเครื่องวัดกระแสไฟฟ้า PMMC block diagram ของเครื่องวิเคราะห์คลื่นพื้นฐานแสดงไว้ในรูปด้านล่าง -
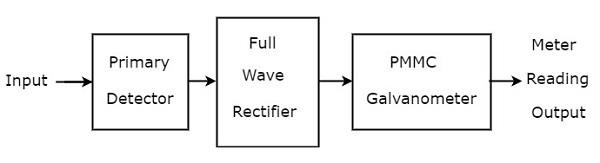
function ของแต่ละบล็อกที่มีอยู่ในเครื่องวิเคราะห์คลื่นพื้นฐานจะกล่าวถึงด้านล่าง
Primary Detector- ประกอบด้วยวงจร LC เราสามารถปรับค่าของตัวเหนี่ยวนำ, L และตัวเก็บประจุ, C ในลักษณะที่อนุญาตเฉพาะส่วนประกอบความถี่ฮาร์มอนิกที่ต้องการเท่านั้นที่จะวัดได้
Full Wave Rectifier - แปลงอินพุต AC เป็นเอาต์พุต DC
PMMC Galvanometer - แสดงค่าสูงสุดของสัญญาณซึ่งได้รับจากเอาต์พุตของ Full wave rectifier
เราจะได้แผนภาพวงจรที่เกี่ยวข้องเพียงแค่แทนที่แต่ละบล็อกด้วยส่วนประกอบตามลำดับในแผนภาพบล็อกด้านบนของเครื่องวิเคราะห์คลื่นพื้นฐาน ดังนั้นcircuit diagram ของเครื่องวิเคราะห์คลื่นพื้นฐานจะมีลักษณะดังแสดงในรูปต่อไปนี้ -
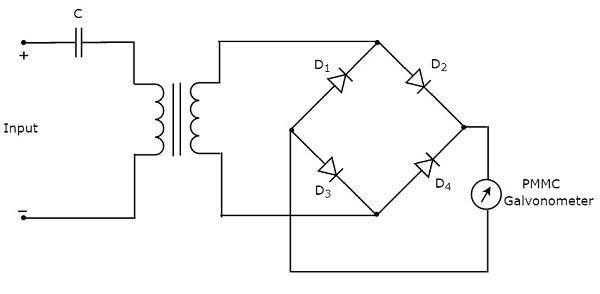
เครื่องวิเคราะห์คลื่นพื้นฐานนี้สามารถใช้ในการวิเคราะห์ส่วนประกอบความถี่ฮาร์มอนิกของสัญญาณคาบ
ประเภทของเครื่องวิเคราะห์คลื่น
เครื่องวิเคราะห์คลื่นสามารถแบ่งออกได้ดังต่อไปนี้ two types.
- เครื่องวิเคราะห์คลื่นความถี่เลือก
- Superheterodyne Wave Analyzer
ตอนนี้ให้เราพูดคุยเกี่ยวกับเครื่องวิเคราะห์คลื่นสองตัวนี้ทีละตัว
เครื่องวิเคราะห์คลื่นความถี่เลือก
เครื่องวิเคราะห์คลื่นที่ใช้ในการวิเคราะห์สัญญาณอยู่ในช่วง AF เรียกว่าเครื่องวิเคราะห์คลื่นความถี่เลือก block diagram ของเครื่องวิเคราะห์คลื่นความถี่เลือกแสดงดังรูปด้านล่าง
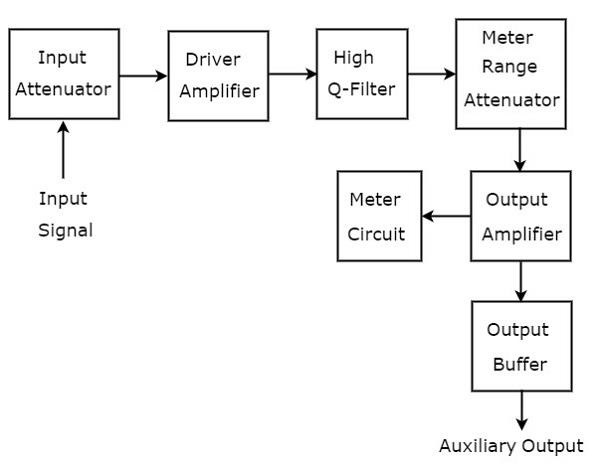
เครื่องวิเคราะห์คลื่นความถี่เลือกประกอบด้วยชุดบล็อก function ของแต่ละบล็อกจะกล่าวถึงด้านล่าง
Input Attenuator- สัญญาณ AF ซึ่งจะวิเคราะห์จะถูกนำไปใช้กับตัวลดทอนอินพุต หากแอมพลิจูดของสัญญาณมีขนาดใหญ่เกินไปก็สามารถลดทอนได้โดยตัวลดทอนอินพุต
Driver Amplifier - ขยายสัญญาณที่ได้รับเมื่อจำเป็น
High Q-filter- ใช้เพื่อเลือกความถี่ที่ต้องการและปฏิเสธความถี่ที่ไม่ต้องการ ประกอบด้วยส่วน RC สองส่วนและแอมพลิฟายเออร์ตัวกรองสองตัวและทั้งหมดนี้เรียงซ้อนกัน เราสามารถเปลี่ยนค่าความจุสำหรับการเปลี่ยนช่วงของความถี่เป็นกำลัง 10 ในทำนองเดียวกันเราสามารถเปลี่ยนค่าความต้านทานเพื่อเปลี่ยนความถี่ภายในช่วงที่เลือกได้
Meter Range Attenuator - รับสัญญาณ AF ที่เลือกเป็นอินพุตและสร้างเอาต์พุตที่ลดทอนเมื่อใดก็ตามที่ต้องการ
Output Amplifier - จะขยายสัญญาณ AF ที่เลือกหากจำเป็น
Output Buffer - ใช้เพื่อให้สัญญาณ AF ที่เลือกไปยังอุปกรณ์ส่งออก
Meter Circuit- แสดงการอ่านสัญญาณ AF ที่เลือก เราสามารถเลือกการอ่านมิเตอร์ในช่วงโวลต์หรือช่วงเดซิเบล
Superheterodyne Wave Analyzer
เครื่องวิเคราะห์คลื่นที่ใช้ในการวิเคราะห์สัญญาณของช่วง RF เรียกว่าเครื่องวิเคราะห์คลื่น superheterodyne รูปต่อไปนี้แสดงไฟล์block diagram ของเครื่องวิเคราะห์คลื่น superheterodyne
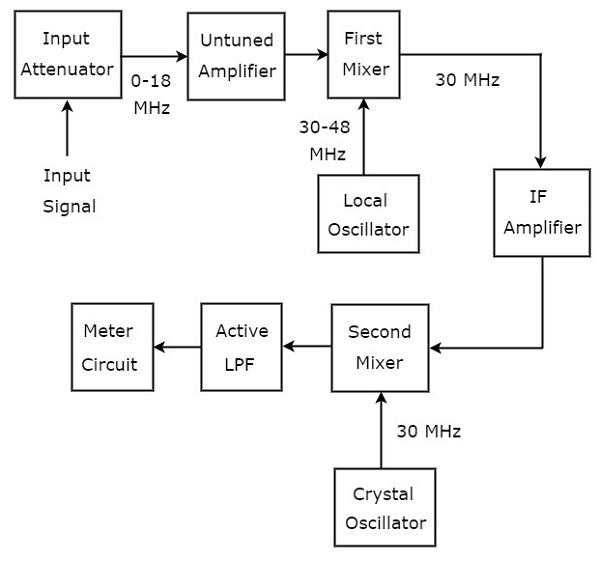
working ของเครื่องวิเคราะห์คลื่น superheterodyne มีการระบุไว้ด้านล่าง
สัญญาณ RF ที่จะวิเคราะห์จะถูกนำไปใช้กับตัวลดทอนอินพุต หากแอมพลิจูดของสัญญาณมีขนาดใหญ่เกินไปก็สามารถลดทอนได้input attenuator.
Untuned amplifier ขยายสัญญาณ RF ทุกครั้งที่จำเป็นและใช้กับมิกเซอร์ตัวแรก
ช่วงความถี่ของสัญญาณ RF และเอาต์พุตของ Local oscillator คือ 0-18 MHz และ 30-48 MHz ตามลำดับ ดังนั้น,first mixerสร้างเอาต์พุตซึ่งมีความถี่ 30 MHz นี่คือความแตกต่างของความถี่ของสัญญาณทั้งสองที่ใช้กับมัน
IF amplifierขยายสัญญาณความถี่กลาง (IF) นั่นคือเอาต์พุตของมิกเซอร์ตัวแรก สัญญาณ IF ที่ขยายถูกนำไปใช้กับมิกเซอร์ตัวที่สอง
ความถี่ของสัญญาณ IF ที่ขยายและเอาต์พุตของ Crystal oscillator นั้นเท่ากันและเท่ากับ 30MHz ดังนั้นsecond mixerสร้างเอาต์พุตซึ่งมีความถี่ 0 Hz นี่คือความแตกต่างของความถี่ของสัญญาณทั้งสองที่ใช้กับมัน
ความถี่ในการตัดของ Active Low Pass Filter (LPF)ถูกเลือกเป็น 1500 Hz ดังนั้นตัวกรองนี้จึงให้สัญญาณเอาต์พุตของมิกเซอร์ตัวที่สอง
Meter Circuitแสดงการอ่านสัญญาณ RF เราสามารถเลือกการอ่านมิเตอร์ในช่วงโวลต์หรือช่วงเดซิเบล
ดังนั้นเราจึงสามารถเลือกเครื่องวิเคราะห์คลื่นเฉพาะตามช่วงความถี่ของสัญญาณที่จะวิเคราะห์ได้
เครื่องมืออิเล็กทรอนิกส์ที่ใช้ในการวิเคราะห์คลื่นในโดเมนความถี่เรียกว่า spectrum analyzer. โดยทั่วไปจะแสดงการกระจายพลังงานของสัญญาณบนหน้าจอ CRT ในที่นี้แกน x แสดงถึงความถี่และแกน y แสดงถึงแอมพลิจูด
ประเภทของเครื่องวิเคราะห์สเปกตรัม
เราสามารถแบ่งประเภทของเครื่องวิเคราะห์สเปกตรัมได้ดังต่อไปนี้ two types.
- กรองเครื่องวิเคราะห์สเปกตรัมของธนาคาร
- เครื่องวิเคราะห์สเปกตรัม Superheterodyne
ตอนนี้ให้เราพูดคุยเกี่ยวกับเครื่องวิเคราะห์สเปกตรัมทั้งสองนี้ทีละตัว
กรองเครื่องวิเคราะห์สเปกตรัมของธนาคาร
เครื่องวิเคราะห์สเปกตรัมที่ใช้ในการวิเคราะห์สัญญาณอยู่ในช่วง AF เรียกว่าเครื่องวิเคราะห์สเปกตรัมของธนาคารกรองหรือ real time spectrum analyzer เนื่องจากแสดง (แสดง) รูปแบบใด ๆ ในความถี่อินพุตทั้งหมด
รูปต่อไปนี้แสดงไฟล์ block diagram ของเครื่องวิเคราะห์สเปกตรัมของธนาคารกรอง
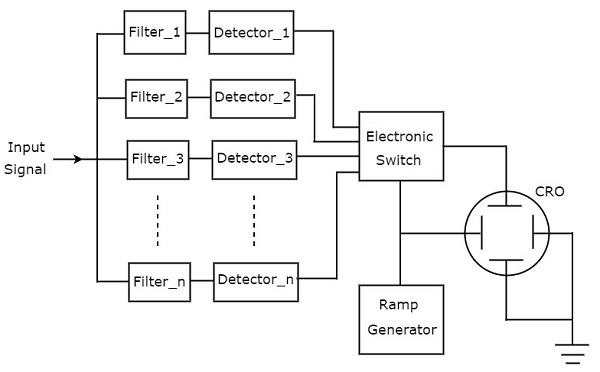
working ของเครื่องวิเคราะห์สเปกตรัมของธนาคารกรองระบุไว้ด้านล่าง
มันมีชุดของตัวกรองแบนด์พาสและแต่ละตัวได้รับการออกแบบมาเพื่อให้ย่านความถี่เฉพาะ เอาต์พุตของแต่ละแบนด์พาสฟิลเตอร์มอบให้กับเครื่องตรวจจับที่เกี่ยวข้อง
เอาต์พุตเครื่องตรวจจับทั้งหมดเชื่อมต่อกับสวิตช์อิเล็กทรอนิกส์ สวิตช์นี้ช่วยให้เครื่องตรวจจับเอาต์พุตตามลำดับไปยังแผ่นโก่งในแนวตั้งของ CRO ดังนั้น CRO จะแสดงความถี่spectrum of AF signal บนหน้าจอ CRT
เครื่องวิเคราะห์สเปกตรัม Superheterodyne
เรียกว่าเครื่องวิเคราะห์สเปกตรัมที่ใช้ในการวิเคราะห์สัญญาณเป็นช่วง RF superheterodyne spectrum analyzer. มันblock diagram ดังแสดงในรูปด้านล่าง
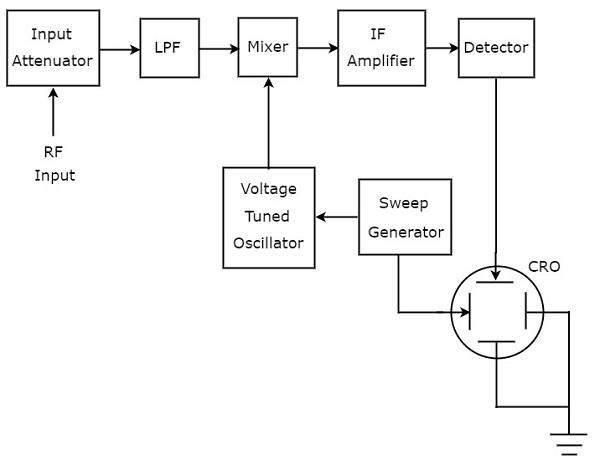
working ของเครื่องวิเคราะห์สเปกตรัม superheterodyne มีการระบุไว้ด้านล่าง
สัญญาณ RF ที่จะวิเคราะห์จะถูกนำไปใช้กับตัวลดทอนอินพุต หากแอมพลิจูดของสัญญาณมีขนาดใหญ่เกินไปก็สามารถลดทอนได้ด้วยinput attenuator.
Low Pass Filter (LPF) อนุญาตเฉพาะส่วนประกอบความถี่ที่น้อยกว่าความถี่ตัด
Mixerรับอินพุตจากตัวกรองความถี่ต่ำและออสซิลเลเตอร์ที่ปรับแรงดันไฟฟ้า สร้างเอาต์พุตซึ่งเป็นความแตกต่างของความถี่ของสัญญาณทั้งสองที่ใช้กับมัน
IF amplifierขยายสัญญาณความถี่กลาง (IF) คือเอาต์พุตของมิกเซอร์ สัญญาณ IF ที่ขยายถูกนำไปใช้กับเครื่องตรวจจับ
เอาต์พุตของเครื่องตรวจจับมอบให้กับแผ่นโก่งในแนวตั้งของ CRO ดังนั้น CRO จะแสดงความถี่spectrum of RF signal บนหน้าจอ CRT
ดังนั้นเราจึงสามารถเลือกเครื่องวิเคราะห์สเปกตรัมเฉพาะตามช่วงความถี่ของสัญญาณที่จะวิเคราะห์ได้
Oscilloscopeเป็นอุปกรณ์อิเล็กทรอนิกส์ซึ่งแสดงรูปคลื่นแรงดันไฟฟ้า ในบรรดาออสซิลโลสโคปแคโทดเรย์ออสซิลโลสโคป (CRO) เป็นเครื่องพื้นฐานและแสดงสัญญาณหรือรูปคลื่นที่แตกต่างกันไปตามเวลา
ในบทนี้ให้เราพูดคุยเกี่ยวกับแผนภาพบล็อกของ CRO และการวัดพารามิเตอร์บางอย่างโดยใช้ CRO
แผนภาพบล็อกของ CRO
Cathode Ray Oscilloscope (CRO) ประกอบด้วยชุดบล็อก เหล่านี้คือแอมพลิฟายเออร์แนวตั้งสายหน่วงวงจรทริกเกอร์เครื่องกำเนิดฐานเวลาเครื่องขยายเสียงแนวนอนหลอดแคโทดเรย์ (CRT) และแหล่งจ่ายไฟ block diagram ของ CRO แสดงดังรูปด้านล่าง
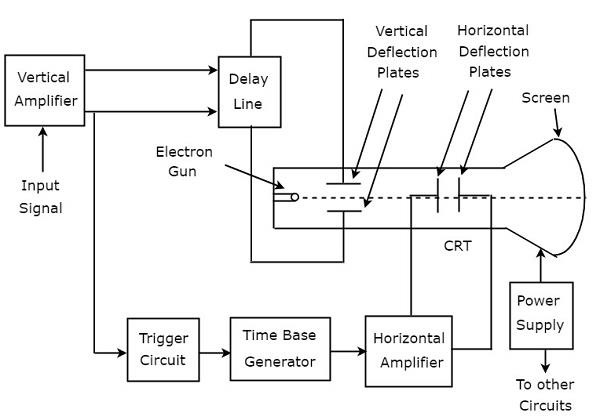
function ของแต่ละบล็อกของ CRO มีการระบุไว้ด้านล่าง
Vertical Amplifier - ขยายสัญญาณอินพุตซึ่งจะแสดงบนหน้าจอของ CRT
Delay Line- ให้สัญญาณล่าช้าจำนวนหนึ่งซึ่งได้รับจากเอาต์พุตของเครื่องขยายเสียงแนวตั้ง จากนั้นสัญญาณล่าช้านี้จะถูกนำไปใช้กับแผ่นโก่งในแนวตั้งของ CRT
Trigger Circuit - สร้างสัญญาณทริกเกอร์เพื่อซิงโครไนซ์การเบี่ยงเบนของลำแสงอิเล็กตรอนทั้งแนวนอนและแนวตั้ง
Time base Generator - สร้างสัญญาณฟันเลื่อยซึ่งมีประโยชน์สำหรับการเบี่ยงเบนของลำแสงอิเล็กตรอนในแนวนอน
Horizontal Amplifier - ขยายสัญญาณฟันเลื่อยจากนั้นเชื่อมต่อกับแผ่นโก่งแนวนอนของ CRT
Power supply- ผลิตทั้งแรงดันไฟฟ้าสูงและต่ำ แรงดันไฟฟ้าสูงเชิงลบและแรงดันไฟฟ้าต่ำที่เป็นบวกจะถูกนำไปใช้กับ CRT และวงจรอื่น ๆ ตามลำดับ
Cathode Ray Tube (CRT)- เป็นบล็อกสำคัญที่สำคัญของ CRO และส่วนใหญ่ประกอบด้วยสี่ส่วน สิ่งเหล่านี้คือปืนอิเล็กตรอนแผ่นโก่งในแนวตั้งแผ่นโก่งแนวนอนและหน้าจอเรืองแสง
ลำแสงอิเล็กตรอนซึ่งผลิตโดยปืนอิเล็กตรอนจะหักเหทั้งในแนวตั้งและแนวนอนโดยแผ่นโก่งในแนวตั้งคู่หนึ่งและแผ่นโก่งแนวนอนตามลำดับ สุดท้ายลำแสงที่เบี่ยงเบนจะปรากฏเป็นจุดบนหน้าจอเรืองแสง
ด้วยวิธีนี้ CRO จะแสดงสัญญาณอินพุตที่ใช้บนหน้าจอของ CRT ดังนั้นเราสามารถวิเคราะห์สัญญาณในโดเมนเวลาโดยใช้ CRO
การวัดโดยใช้ CRO
เราสามารถทำการวัดต่อไปนี้โดยใช้ CRO
- การวัดแอมพลิจูด
- การวัดช่วงเวลา
- การวัดความถี่
ตอนนี้ให้เราพูดคุยเกี่ยวกับการวัดเหล่านี้ทีละรายการ
การวัดแอมพลิจูด
CRO แสดงสัญญาณแรงดันไฟฟ้าตามฟังก์ชันของเวลาบนหน้าจอ amplitude ของสัญญาณแรงดันไฟฟ้านั้นคงที่ แต่เราสามารถเปลี่ยนจำนวนหน่วยงานที่ครอบคลุมสัญญาณแรงดันไฟฟ้าในแนวตั้งได้โดยแตกต่างกันไป volt/divisionลูกบิดบนแผง CRO ดังนั้นเราจะได้รับไฟล์amplitude ของสัญญาณที่ปรากฏบนหน้าจอของ CRO โดยใช้สูตรต่อไปนี้
$$ A = j \ times n_ {v} $$
ที่ไหน
$ A $ คือแอมพลิจูด
$ j $ คือค่าของโวลต์ / การหาร
$ n_ {v} $ คือจำนวนหน่วยงานที่ครอบคลุมสัญญาณในแนวตั้ง
การวัดช่วงเวลา
CRO แสดงสัญญาณแรงดันไฟฟ้าตามฟังก์ชันของเวลาบนหน้าจอ Time period ของสัญญาณแรงดันไฟฟ้าเป็นระยะนั้นคงที่ แต่เราสามารถเปลี่ยนจำนวนหน่วยงานที่ครอบคลุมสัญญาณแรงดันไฟฟ้าครบวงจรหนึ่งรอบในแนวนอนได้โดยการแปรผัน time/division ลูกบิดบนแผง CRO
ดังนั้นเราจะได้รับไฟล์ Time period ของสัญญาณที่ปรากฏบนหน้าจอของ CRO โดยใช้สูตรต่อไปนี้
$$ T = k \ times n_ {h} $$
ที่ไหน
$ T $ คือช่วงเวลา
$ j $ คือมูลค่าของเวลา / การหาร
$ n_ {v} $ คือจำนวนหน่วยงานที่ครอบคลุมหนึ่งรอบที่สมบูรณ์ของสัญญาณธาตุในแนวนอน
การวัดความถี่
ความถี่ f ของสัญญาณเป็นระยะคือช่วงเวลาซึ่งกันและกัน T. Mathematicallyสามารถแสดงเป็น
$$ f = \ frac {1} {T} $$
ดังนั้นเราสามารถหาความถี่ f ของสัญญาณเป็นระยะได้โดยทำตามสองขั้นตอนนี้
Step1 - ค้นหาไฟล์ Time period ของสัญญาณเป็นระยะ
Step2 - รับ reciprocal ของช่วงเวลาของสัญญาณเป็นระยะซึ่งได้รับในขั้นตอนที่ 1
เราจะพูดถึงออสซิลโลสโคปวัตถุประสงค์พิเศษในบทถัดไป
ในบทที่แล้วเราได้พูดถึง Cathode Ray Oscilloscope (CRO) ซึ่งเป็นออสซิลโลสโคปพื้นฐาน เราจะได้รับออสซิลโลสโคปแบบพิเศษเพียงแค่รวมบล็อกเพิ่มเติมสองสามชิ้นเข้ากับออสซิลโลสโคปพื้นฐานตามข้อกำหนด
ต่อไปนี้คือไฟล์ special purpose oscilloscopes.
- Dual Beam Oscilloscope
- Dual Trace Oscilloscope
- ออสซิลโลสโคปแบบดิจิตอล
ตอนนี้ให้เราพูดคุยเกี่ยวกับออสซิลโลสโคปวัตถุประสงค์พิเศษเหล่านี้ทีละตัว
Dual Beam Oscilloscope
ออสซิลโลสโคปซึ่งแสดงรูปคลื่นแรงดันไฟฟ้าสองรูปเรียกว่า Dual Beam Oscilloscope มันblock diagram ดังแสดงในรูปด้านล่าง
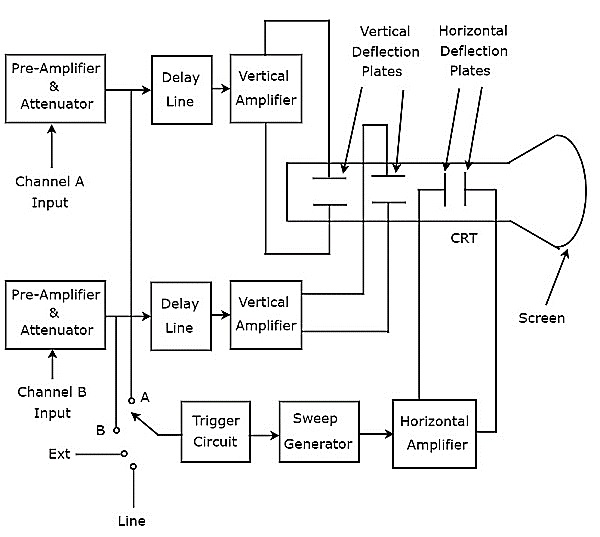
ดังแสดงในรูปด้านบน CRT ของ Dual Beam Oscilloscope ประกอบด้วยแผ่นโก่งในแนวตั้งสองชุดและแผ่นโก่งแนวนอนหนึ่งชุด
การรวมบล็อกต่อไปนี้เข้าด้วยกันเรียกว่า a channel.
- ปรีแอมป์และตัวลดทอน
- สายล่าช้า
- เครื่องขยายเสียงแนวตั้ง
- ชุดแผ่นเบี่ยงแนวตั้ง
มีสองช่องสัญญาณใน Dual Beam Oscilloscope ดังนั้นเราสามารถใช้สองสัญญาณคือ A & B เป็นอินพุตของช่อง A และช่อง B ตามลำดับ เราสามารถเลือกหนึ่งในสี่สัญญาณนี้เป็นtrigger inputไปยังวงจรทริกเกอร์โดยใช้สวิตช์ นั่นคือสัญญาณอินพุต A & B, สัญญาณภายนอก (Ext) และอินพุตสาย
ออสซิลโลสโคปนี้จะสร้างคานที่เบี่ยงเบนในแนวตั้งสองชิ้นเนื่องจากมีแผ่นโก่งในแนวตั้งสองคู่ ในออสซิลโลสโคปนี้บล็อกที่มีประโยชน์สำหรับการเบี่ยงเบนลำแสงในแนวนอนเป็นเรื่องปกติสำหรับทั้งสัญญาณอินพุต ในที่สุดออสซิลโลสโคปนี้จะสร้างไฟล์two input signals พร้อมกันบนหน้าจอของ CRT
Dual Trace Oscilloscope
ออสซิลโลสโคปซึ่งสร้างสองร่องรอยบนหน้าจอเรียกว่า Dual Trace Oscilloscope มันblock diagram ดังแสดงในรูปด้านล่าง
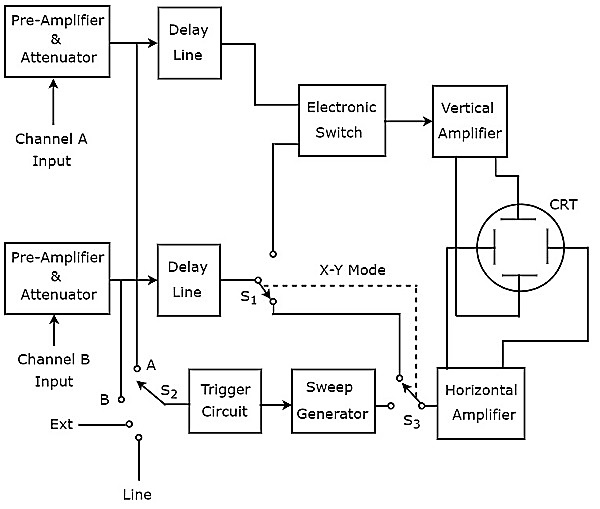
ดังแสดงในรูปด้านบน CRT ของ Dual Trace Oscilloscope ประกอบด้วยชุดแผ่นโก่งในแนวตั้งและแผ่นโก่งแนวนอนอีกชุดหนึ่ง แชนเนลประกอบด้วยสี่บล็อก ได้แก่ พรีแอมป์และตัวลดทอนสัญญาณหน่วงเวลาแอมพลิฟายเออร์แนวตั้งและแผ่นโก่งในแนวตั้ง
ในแผนภาพด้านบนสองบล็อกแรกจะแสดงแยกกันในทั้งสองช่อง สองบล็อกสุดท้ายเป็นเรื่องปกติสำหรับทั้งสองช่อง ดังนั้นด้วยความช่วยเหลือของelectronic switch เราสามารถเชื่อมต่อเอาต์พุตสายหน่วงเวลาของช่องเฉพาะกับเครื่องขยายเสียงแนวตั้ง
เราสามารถเลือกหนึ่งในสี่สัญญาณนี้เป็นอินพุตทริกเกอร์ไปยังไฟล์ trigger circuitโดยใช้สวิตช์ นั่นคือสัญญาณอินพุต A & B, สัญญาณภายนอก (Ext) และอินพุตสาย
ออสซิลโลสโคปนี้ใช้ลำแสงอิเล็กตรอนเดียวกันในการเบี่ยงเบนสัญญาณอินพุต A & B ในแนวตั้งโดยใช้สวิตช์อิเล็กทรอนิกส์และสร้าง two traces. บล็อกที่เบี่ยงเบนลำแสงในแนวนอนเป็นเรื่องปกติสำหรับทั้งสัญญาณอินพุต
ออสซิลโลสโคปแบบดิจิตอล
ออสซิลโลสโคปซึ่งเก็บรูปคลื่นแบบดิจิทัลเรียกว่าออสซิลโลสโคปแบบดิจิตอล block diagram ของออสซิลโลสโคปจัดเก็บข้อมูล (ดิจิตอล) อยู่ด้านล่าง -
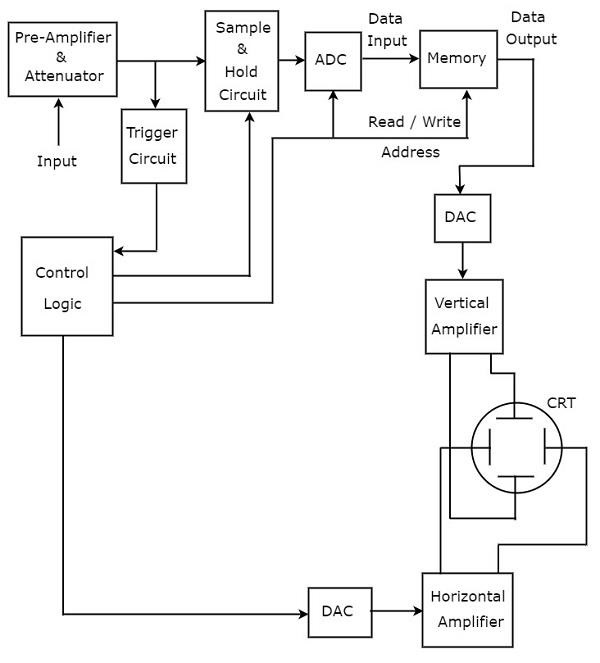
บล็อกเพิ่มเติมที่จำเป็นสำหรับการจัดเก็บข้อมูลดิจิทัลจะถูกเพิ่มลงในออสซิลโลสโคปพื้นฐานเพื่อแปลงเป็น Digital Storage Oscilloscope บล็อกที่จำเป็นสำหรับstoring of digital dataอยู่ระหว่างพรีแอมพลิฟายเออร์และตัวลดทอนและแอมพลิฟายเออร์แนวตั้งใน Digital Storage Oscilloscope เหล่านี้คือวงจรตัวอย่างและ Hold, ตัวแปลงอนาล็อกเป็นดิจิตอล (ADC), หน่วยความจำและตัวแปลงดิจิตอลเป็นอนาล็อก
Control logicควบคุมสามบล็อกแรกโดยการส่งสัญญาณควบคุมต่างๆ บล็อกเช่นตรรกะการควบคุมและตัวแปลงดิจิตอลเป็นอนาล็อกมีอยู่ระหว่างวงจรทริกเกอร์และแอมพลิฟายเออร์แนวนอนใน Digital Storage Oscilloscope
ออสซิลโลสโคปแบบดิจิตอล stores the dataในระบบดิจิตอลก่อนที่จะแสดงรูปคลื่นบนหน้าจอ ในขณะที่ออสซิลโลสโคปพื้นฐานไม่มีคุณสมบัตินี้
Lissajous figureคือรูปแบบที่แสดงบนหน้าจอเมื่อใช้สัญญาณไซน์กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO รูปแบบเหล่านี้จะแตกต่างกันไปตามแอมพลิจูดความถี่และความแตกต่างของเฟสของสัญญาณไซน์ซึ่งใช้กับแผ่นโก่งในแนวนอนและแนวตั้งของ CRO
รูปต่อไปนี้แสดงไฟล์ example ของร่าง Lissajous
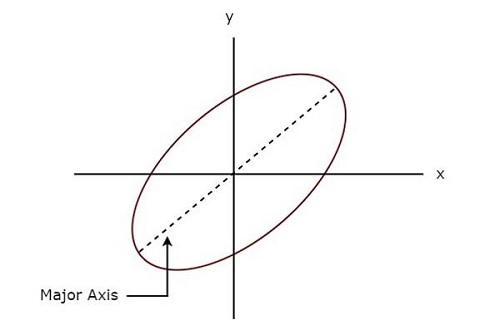
ร่าง Lissajous ด้านบนอยู่ใน elliptical shape และแกนหลักของมันมีมุมเอียงกับแกน x ที่เป็นบวก
การวัดโดยใช้ Lissajous Figures
เราสามารถทำได้ดังต่อไปนี้ two measurements จากร่าง Lissajous
- ความถี่ของสัญญาณไซน์
- ความแตกต่างของเฟสระหว่างสัญญาณไซน์สองตัว
ตอนนี้ให้เราพูดคุยเกี่ยวกับการวัดทั้งสองนี้ทีละรายการ
การวัดความถี่
รูปลิสซาจัสจะแสดงบนหน้าจอเมื่อสัญญาณไซน์ถูกนำไปใช้กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO ดังนั้นใช้สัญญาณไซน์ซึ่งมีมาตรฐานknown frequencyไปยังแผ่นโก่งแนวนอนของ CRO ในทำนองเดียวกันให้ใช้สัญญาณรูปซายน์ซึ่งfrequency คือ unknown ไปยังแผ่นโก่งในแนวตั้งของ CRO
ให้ $ f_ {H} $ และ $ f_ {V} $ เป็นความถี่ของสัญญาณไซน์ซึ่งใช้กับแผ่นเบี่ยงเบนแนวนอนและแนวตั้งของ CRO ตามลำดับ ความสัมพันธ์ระหว่าง $ f_ {H} $ และ $ f_ {V} $ สามารถเป็นได้mathematically แสดงเป็นด้านล่าง
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
จากความสัมพันธ์ข้างต้นเราจะได้ความถี่ของสัญญาณไซน์ซึ่งนำไปใช้กับแผ่นโก่งในแนวตั้งของ CRO เป็น
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (สมการ 1)
ที่ไหน
$ n_ {H} $ คือจำนวนของเส้นสัมผัสแนวนอน
$ n_ {V} $ คือจำนวนของเส้นสัมผัสแนวตั้ง
เราสามารถหาค่าของ $ n_ {H} $ และ $ n_ {V} $ ได้จากรูป Lissajous ดังนั้นโดยการแทนที่ค่าของ $ n_ {H} $, $ n_ {V} $ และ $ f_ {H} $ ในสมการ 1 เราจะได้ค่าของ$f_{V}$กล่าวคือ frequency of sinusoidal signal ที่ใช้กับแผ่นโก่งในแนวตั้งของ CRO
การวัดความแตกต่างของเฟส
รูปลิสซาจัสจะปรากฏบนหน้าจอเมื่อใช้สัญญาณไซน์กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO ดังนั้นใช้สัญญาณไซน์ซึ่งมีsame amplitude and frequency ไปยังแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO
สำหรับตัวเลข Lissajous เพียงไม่กี่ตัวตามรูปร่างเราสามารถบอกความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองได้โดยตรง
ถ้าร่าง Lissajous เป็น straight line โดยมีความเอียง $ 45 ^ {\ circ} $ พร้อมแกน x ที่เป็นค่าบวกจากนั้น phase differenceระหว่างสัญญาณไซน์ทั้งสองจะเท่ากับ $ 0 ^ {\ circ} $ นั่นหมายความว่าไม่มีความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองนี้
ถ้าร่าง Lissajous เป็น straight line โดยมีค่าเอียง $ 135 ^ {\ circ} $ พร้อมแกน x บวกตามด้วย phase differenceระหว่างสัญญาณไซน์ทั้งสองจะเท่ากับ $ 180 ^ {\ circ} $ นั่นหมายความว่าสัญญาณไซน์ทั้งสองนี้อยู่นอกเฟส
ถ้าร่าง Lissajous อยู่ใน circular shapeดังนั้นความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น $ 90 ^ {\ circ} $ หรือ $ 270 ^ {\ circ} $
เราสามารถคำนวณความแตกต่างของเฟสระหว่างสัญญาณไซน์สองตัวได้โดยใช้สูตรเมื่อมีตัวเลขลิสซาจัส elliptical shape.
ถ้าแกนหลักของรูปทรงรีรูปลิสซาจัสที่มีมุมเอียงอยู่ระหว่าง $ 0 ^ {\ circ} $ และ $ 90 ^ {\ circ} $ กับแกน x บวกความแตกต่างเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น
$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$
ถ้าแกนหลักของรูปทรงรีรูปลิสซาจัสที่มีมุมเอียงอยู่ระหว่าง $ 90 ^ {\ circ} $ และ $ 180 ^ {\ circ} $ กับแกน x ที่เป็นบวกความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น
$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$
Where,
$ x_ {1} $ คือระยะทางจากจุดเริ่มต้นถึงจุดบนแกน x โดยที่รูปลิสซาจัสรูปวงรีตัดกัน
$ x_ {2} $ คือระยะห่างจากจุดเริ่มต้นถึงเส้นสัมผัสแนวตั้งของรูปทรงรีรูปลิสซาจัส
$ y_ {1} $ คือระยะทางจากจุดกำเนิดถึงจุดบนแกน y โดยที่รูปลิสซาจัสรูปวงรีตัดกัน
$ y_ {2} $ คือระยะทางจากจุดเริ่มต้นถึงเส้นสัมผัสแนวนอนของรูปทรงรีรูปลิสซาจัส
ในบทนี้จะอธิบายถึงวิธีการหาความถี่ของสัญญาณไซน์ที่ไม่ทราบสาเหตุและความแตกต่างของเฟสระหว่างสัญญาณไซน์สองตัวจากตัวเลขลิสซาจัสโดยใช้สูตร
เราสามารถเชื่อมต่อวงจรทดสอบใด ๆ เข้ากับออสซิลโลสโคปผ่านหัววัด เนื่องจาก CRO เป็นออสซิลโลสโคปพื้นฐานจึงเรียกโพรบที่เชื่อมต่ออยู่ด้วยCRO probe.
เราควรเลือกโพรบในลักษณะที่ไม่ควรสร้างปัญหาในการโหลดกับวงจรทดสอบ เพื่อให้เราสามารถวิเคราะห์วงจรทดสอบด้วยสัญญาณได้อย่างถูกต้องบนหน้าจอ CRO
โพรบ CRO ควรมีดังต่อไปนี้ characteristics.
- ความต้านทานสูง
- แบนด์วิดท์สูง
block diagram ของโพรบ CRO แสดงไว้ในรูปด้านล่าง
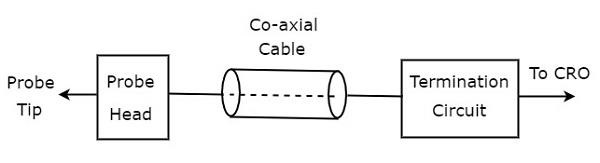
ดังแสดงในรูปหัววัด CRO ส่วนใหญ่ประกอบด้วยสามบล็อก คือหัวโพรบสายแกนร่วมและวงจรเลิกจ้าง สายเคเบิลแกนร่วมเพียงแค่เชื่อมต่อหัวโพรบและวงจรเลิกจ้าง
ประเภทของ CRO Probes
หัววัด CRO สามารถแบ่งออกได้ดังต่อไปนี้ two types.
- Passive Probes
- Active Probes
ตอนนี้ให้เราพูดคุยเกี่ยวกับโพรบทั้งสองประเภทนี้ทีละประเภท
Passive Probes
หากหัวโพรบประกอบด้วยองค์ประกอบแบบพาสซีฟจะเรียกว่า passive probe. แผนภาพวงจรของโพรบแบบพาสซีฟแสดงไว้ในรูปด้านล่าง
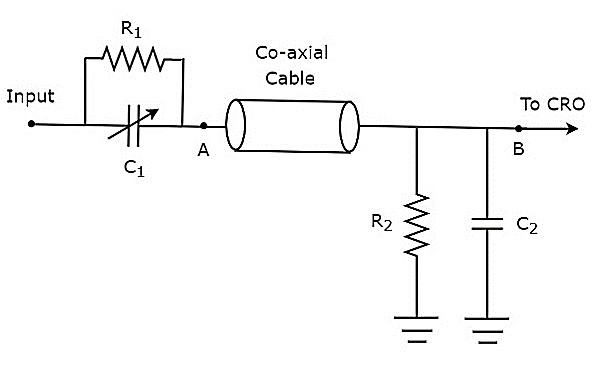
ดังแสดงในรูปหัวโพรบประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุแบบแปรผัน $ C_ {1} $ ในทำนองเดียวกันวงจรเลิกจ้างประกอบด้วยชุดตัวต้านทานแบบขนาน $ R_ {2} $ และตัวเก็บประจุ $ C_ {2} $
แผนภาพวงจรข้างต้นได้รับการแก้ไขในรูปแบบของ bridge circuit และแสดงในรูปด้านล่าง
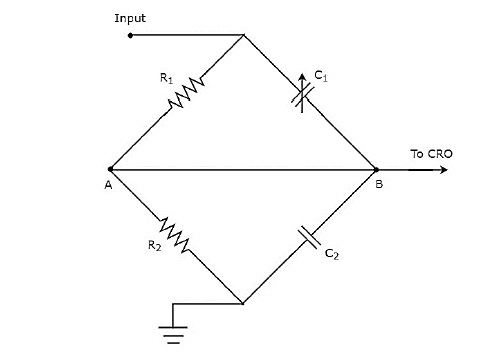
เราสามารถบาลานซ์บริดจ์ได้โดยการปรับค่าของตัวเก็บประจุแบบแปรผัน $ c_ {1} $ เราจะพูดถึงแนวคิดของสะพานในบทต่อไปนี้ ในขณะนี้ให้พิจารณาสิ่งต่อไปนี้balancing condition of AC bridge.
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
Substitute, อิมพีแดนซ์ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เท่ากับ $ R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ { 2} $ และ $ \ frac {1} {j \ omega C_ {2}} $ ตามลำดับในสมการด้านบน
$$ R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ right) R_ {2 } $$
$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $ สมการ 1
ตามหลักการแบ่งแรงดันเราจะได้ voltage across resistor, $R_{2}$ เช่น
$$ V_ {0} = V_ {i} \ left (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ right) $$
attenuation factorคืออัตราส่วนของแรงดันไฟฟ้าอินพุต $ V_ {i} $ และแรงดันขาออก $ V_ {0} $ ดังนั้นจากสมการด้านบนเราจะได้ปัจจัยการลดทอน $ \ alpha $ as
$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$
$ \ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $
$ \ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $
$ \ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2} $ สมการ 2
จากสมการ 2 เราสามารถสรุปได้ว่าค่าของ $ R_ {1} $ มากกว่าหรือเท่ากับค่าของð ?? '… 2 สำหรับค่าจำนวนเต็มของ $ \: \ alpha> 1 $
แทนสมการ 2 ในสมการ 1
$$ \ left (\ alpha-1 \ right) R_ {2} C_ {1} = R_ {2} C_ {2} $$
$ \ Rightarrow \ left (\ alpha-1 \ right) C_ {1} = C_ {2} $
$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)} $ สมการ 3
จากสมการ 3 เราสามารถสรุปได้ว่าค่าของ $ C_ {1} $ น้อยกว่าหรือเท่ากับค่า $ C_ {2} $ สำหรับค่าจำนวนเต็ม $ \ alpha> 1 $
Example
ให้เราหาค่า $ R_ {1} $ และ $ C_ {1} $ ของโพรบที่มีปัจจัยการลดทอน $ \ alpha $ เป็น 10 สมมติ $ R_ {2} = 1 M \ Omega $ และ $ C_ {2} = 18pF $.
Step1 - เราจะได้รับค่า $ R_ {1} $ โดยแทนที่ค่าของ $ \ alpha $ และ $ R_ {2} $ ในสมการ 2
$$ R_ {1} = \ left (10-1 \ right) \ times 1 \ times 10 ^ {6} $$
$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$
$$ \ Rightarrow R_ {1} = 9 M \ Omega $$
Step 2 - เราจะได้รับค่า $ C_ {1} $ โดยแทนที่ค่าของ $ \ alpha $ และ $ C_ {2} $ ในสมการ 3
$$ C_ {1} = \ frac {18 \ times10 ^ {- 12}} {\ left (10-1 \ right)} $$
$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {- 12} $$
$$ \ Rightarrow C_ {1} = 2 pF $$
ดังนั้นค่าของ $ R_ {1} $ และ $ C_ {1} $ ของโพรบจะเป็น $ 9M \ Omega $ และ $ 2pF $ ตามลำดับสำหรับข้อกำหนดที่กำหนด
Active Probes
หากหัวโพรบประกอบด้วยชิ้นส่วนอิเล็กทรอนิกส์ที่ใช้งานอยู่จะเรียกว่า active probe. แผนภาพบล็อกของโพรบที่ใช้งานอยู่แสดงในรูปด้านล่าง

ดังแสดงในรูปหัวโพรบประกอบด้วยตัวติดตามแหล่งสัญญาณ FET ในน้ำตกที่มีตัวติดตามตัวปล่อย BJT ตัวติดตามแหล่งสัญญาณ FET ให้อิมพีแดนซ์อินพุตสูงและอิมพีแดนซ์เอาต์พุตต่ำ ในขณะที่จุดประสงค์ของผู้ติดตามตัวปล่อย BJT คือการหลีกเลี่ยงหรือกำจัดความไม่ตรงกันของอิมพีแดนซ์
อีกสองส่วนเช่นสายเคเบิลแกนร่วมและวงจรเลิกจ้างยังคงเหมือนเดิมทั้งในโพรบที่ใช้งานและแบบพาสซีฟ
หากอุปกรณ์ไฟฟ้าถูกจัดเรียงในรูปแบบโครงสร้างสะพานหรือวงแหวนวงจรไฟฟ้านั้นเรียกว่า a bridge. โดยทั่วไปสะพานจะสร้างห่วงที่มีแขนหรือกิ่งไม้สี่แขน แต่ละสาขาอาจมีส่วนประกอบไฟฟ้าหนึ่งหรือสองชิ้น
ประเภทของสะพาน
เราสามารถแบ่งประเภทของวงจรบริดจ์หรือบริดจ์ออกเป็นสองประเภทต่อไปนี้โดยพิจารณาจากสัญญาณแรงดันไฟฟ้าที่สามารถใช้งานได้
- สะพาน DC
- สะพาน AC
ตอนนี้ให้เราพูดคุยเกี่ยวกับสะพานทั้งสองนี้สั้น ๆ
สะพาน DC
หากวงจรบริดจ์สามารถทำงานได้ด้วยสัญญาณแรงดันไฟฟ้ากระแสตรงเท่านั้นแสดงว่าเป็นวงจรสะพานกระแสตรงหรือง่ายๆ DC bridge. สะพาน DC ใช้เพื่อวัดค่าของความต้านทานที่ไม่รู้จัก circuit diagram ของสะพาน DC มีลักษณะดังแสดงในรูปด้านล่าง
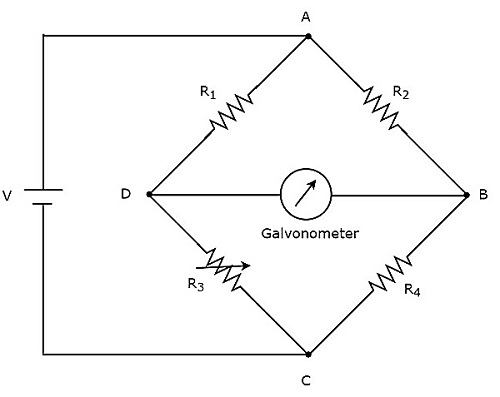
สะพาน DC ด้านบนมี four armsและแขนแต่ละข้างประกอบด้วยตัวต้านทาน ในบรรดาตัวต้านทานสองตัวมีค่าความต้านทานคงที่ตัวต้านทานตัวหนึ่งเป็นตัวต้านทานแบบแปรผันและอีกตัวหนึ่งมีค่าความต้านทานที่ไม่รู้จัก
วงจรสะพาน DC ด้านบนสามารถตื่นเต้นกับ DC voltage sourceโดยวางไว้ในแนวทแยงเดียว กัลวาโนมิเตอร์วางอยู่ในแนวทแยงมุมอื่น ๆ ของสะพาน DC มันแสดงให้เห็นถึงการโก่งตัวตราบเท่าที่สะพานไม่สมดุล
เปลี่ยนค่าความต้านทานของตัวต้านทานตัวแปรจนกว่ากัลวาโนมิเตอร์จะแสดงการโก่งเป็นโมฆะ (ศูนย์) ตอนนี้สะพาน DC ด้านบนถูกกล่าวว่าเป็นแบบสมดุล เราสามารถหาค่าของunknown resistance โดยใช้สมการปม
สะพาน AC
หากวงจรบริดจ์สามารถทำงานได้ด้วยสัญญาณแรงดันไฟฟ้ากระแสสลับเท่านั้นก็จะกล่าวได้ว่าเป็นวงจรสะพานกระแสสลับหรือเรียกง่ายๆ AC bridge. สะพาน AC ใช้เพื่อวัดค่าของความเหนี่ยวนำความจุและความถี่ที่ไม่รู้จัก
circuit diagram ของสะพาน AC มีลักษณะดังแสดงในรูปด้านล่าง

แผนภาพวงจรของสะพาน AC คล้ายกับสะพานกระแสตรง สะพาน AC ด้านบนมีfour armsและแขนแต่ละข้างประกอบด้วยอิมพีแดนซ์บางส่วน นั่นหมายความว่าแต่ละแขนจะมีองค์ประกอบแฝงแบบเดี่ยวหรือแบบผสมเช่นตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุ
ในบรรดาอิมพีแดนซ์ทั้งสี่อิมพีแดนซ์สองตัวมีค่าคงที่อิมพีแดนซ์ตัวหนึ่งเป็นตัวแปรและอีกอิมพีแดนซ์ที่ไม่รู้จัก
วงจรสะพาน AC ด้านบนสามารถตื่นเต้นกับ AC voltage sourceโดยวางไว้ในแนวทแยงเดียว เครื่องตรวจจับวางอยู่ในแนวทแยงมุมอื่น ๆ ของสะพาน AC มันแสดงให้เห็นถึงการโก่งตัวตราบเท่าที่สะพานไม่สมดุล
วงจรสะพาน AC ด้านบนสามารถตื่นเต้นกับ AC voltage sourceโดยวางไว้ในแนวทแยงเดียว เครื่องตรวจจับวางอยู่ในแนวทแยงมุมอื่น ๆ ของสะพาน AC มันแสดงให้เห็นถึงการโก่งตัวตราบเท่าที่สะพานไม่สมดุล
เปลี่ยนค่าอิมพีแดนซ์ของอิมพีแดนซ์ตัวแปรจนกว่าเครื่องตรวจจับจะแสดงการโก่งเป็นโมฆะ (ศูนย์) ตอนนี้สะพาน AC ด้านบนถูกกล่าวว่าเป็นสะพานที่สมดุล เราสามารถหาค่าของunknown impedance โดยใช้สภาวะสมดุล
DC bridgesสามารถใช้งานได้โดยใช้สัญญาณแรงดันไฟฟ้ากระแสตรงเท่านั้น สะพานกระแสตรงมีประโยชน์ในการวัดค่าของความต้านทานที่ไม่รู้จักซึ่งมีอยู่ในสะพาน Wheatstone's Bridge เป็นตัวอย่างของสะพาน DC
ตอนนี้ให้เราพูดคุยเกี่ยวกับ Wheatstone’s Bridge เพื่อหาค่าความต้านทานที่ไม่รู้จัก
สะพานวีทสโตน
สะพานวีทสโตนเป็นสะพานกระแสตรงซึ่งส่วนใหญ่มีแขนทั้งสี่ข้าง แขนทั้งสี่นี้เป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือรูปสี่เหลี่ยมจัตุรัสและแขนแต่ละข้างประกอบด้วยตัวต้านทานหนึ่งตัว
ในการหาค่าความต้านทานที่ไม่รู้จักเราต้องใช้กัลวาโนมิเตอร์และแหล่งจ่ายแรงดันไฟฟ้ากระแสตรง ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของวีทสโตนและอีกอันหนึ่งวางไว้ในแนวทแยงมุมของสะพานวีทสโตน
สะพานของวีทสโตนใช้ในการวัดค่าของความต้านทานปานกลาง circuit diagram ของสะพานวีทสโตนแสดงไว้ในรูปด้านล่าง
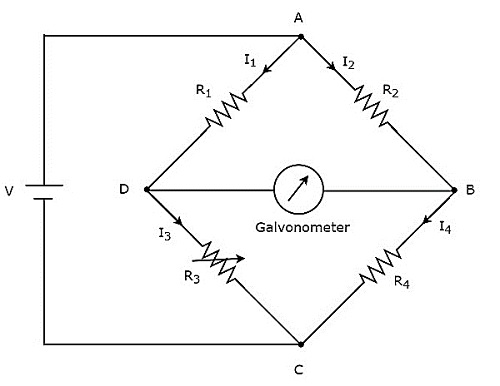
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็น a rhombusหรือรูปทรงสี่เหลี่ยม ประกอบด้วยตัวต้านทาน $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ และ $ R_ {1} $ ตามลำดับ ปล่อยให้กระแสที่ไหลผ่านแขนตัวต้านทานเหล่านี้คือ $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ และ $ I_ {1} $ ตามลำดับและทิศทางของกระแสเหล่านี้จะแสดงในรูป
แขนทแยงมุม DB และ AC ประกอบด้วยกัลวาโนมิเตอร์และแหล่งกำเนิดแรงดันไฟฟ้ากระแสตรงของโวลต์ V ตามลำดับ ที่นี่ตัวต้านทาน $ R_ {3} $ เป็นตัวต้านทานตัวแปรมาตรฐานและตัวต้านทาน $ R_ {4} $ เป็นตัวต้านทานที่ไม่รู้จัก เราทำได้balance the bridgeโดยการเปลี่ยนค่าความต้านทานของตัวต้านทาน $ R_ {3} $
วงจรสะพานด้านบนมีความสมดุลเมื่อไม่มีกระแสไหลผ่านแขนทแยงมุม DB นั่นหมายความว่ามีno deflection ในกัลวาโนมิเตอร์เมื่อสะพานสมดุล
สะพานจะสมดุลเมื่อต่อไปนี้ two conditions พอใจ
แรงดันไฟฟ้าข้ามแขน AD เท่ากับแรงดันไฟฟ้าข้ามแขน AB กล่าวคือ
$$ V_ {AD} = V_ {AB} $$
$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ สมการ 1
แรงดันไฟฟ้าข้ามแขน DC เท่ากับแรงดันไฟฟ้าข้ามแขน BC กล่าวคือ
$$ V_ {DC} = V_ {BC} $$
$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $ สมการ 2
จากเงื่อนไขสมดุลสองประการข้างต้นเราจะได้รับสิ่งต่อไปนี้ two conclusions.
กระแสที่ไหลผ่านแขน AD จะเท่ากับของแขน DC กล่าวคือ
$$ I_ {1} = I_ {3} $$
กระแสที่ไหลผ่านแขน AB จะเท่ากับแขน BC กล่าวคือ
$$ I_ {2} = I_ {4} $$
หาอัตราส่วนของสมการ 1 และสมการ 2
$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ สมการ 3
แทน $ I_ {1} = I_ {3} $ และ $ I_ {2} = I_ {4} $ ในสมการ 3
$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$
$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$
$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
โดยการแทนค่าที่ทราบของตัวต้านทาน $ R_ {1} $, $ R_ {2} $ และ $ R_ {3} $ ในสมการด้านบนเราจะได้ value of resistor,$R_{4}$.
ในบทนี้ให้เราพูดคุยเกี่ยวกับสะพาน AC ซึ่งสามารถใช้ในการวัดความเหนี่ยวนำได้ สะพานไฟฟ้ากระแสสลับทำงานโดยใช้สัญญาณแรงดันไฟฟ้ากระแสสลับเท่านั้น circuit diagram ของสะพาน AC แสดงดังรูปด้านล่าง
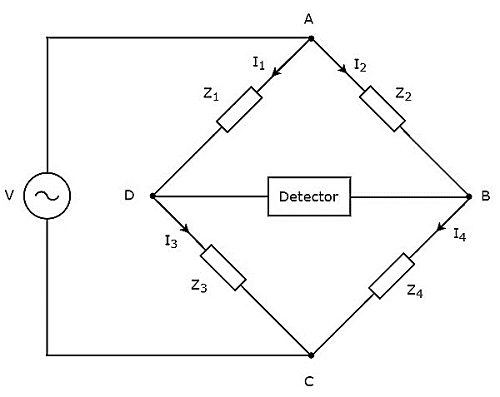
ดังแสดงในรูปด้านบนสะพาน AC ส่วนใหญ่ประกอบด้วยสี่แขนซึ่งเชื่อมต่อกันในรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขนทั้งหมดนี้ประกอบด้วยอิมพีแดนซ์บางส่วน
นอกจากนี้ยังต้องใช้เครื่องตรวจจับและแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับเพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่รู้จัก ดังนั้นหนึ่งในสองตัวนี้วางอยู่ในแนวทแยงมุมของสะพาน AC หนึ่งเส้นและอีกอันหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน AC สภาพสมดุลของสะพานวีทสโตนเป็น -
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
เราจะได้รับไฟล์ balancing condition of AC bridgeเพียงแค่แทนที่ R ด้วย Z ในสมการด้านบน
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
ที่นี่ $ Z_ {1} $ และ $ Z_ {2} $ เป็นอิมพีแดนซ์คงที่ ในขณะที่ $ Z_ {3} $ เป็นอิมพีแดนซ์ตัวแปรมาตรฐานและ $ Z_ {4} $ เป็นอิมพีแดนซ์ที่ไม่รู้จัก
Note - เราสามารถเลือกอิมพีแดนซ์สองตัวจากสี่ตัวนั้นเป็นอิมพีแดนซ์คงที่อิมพีแดนซ์ตัวหนึ่งเป็นอิมพีแดนซ์ตัวแปรมาตรฐานและอิมพีแดนซ์อื่น ๆ เป็นอิมพีแดนซ์ที่ไม่รู้จักตามการใช้งาน
ต่อไปนี้เป็นสะพาน AC สองตัวซึ่งสามารถใช้วัดได้ inductance.
- สะพาน Maxwell
- สะพาน Hay
ตอนนี้ให้เราพูดคุยเกี่ยวกับสะพาน AC สองตัวนี้ทีละตัว
สะพาน Maxwell
สะพานของ Maxwell เป็นสะพาน AC ที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขนสองข้างของสะพานนี้ประกอบด้วยตัวต้านทานเดี่ยวแขนข้างหนึ่งประกอบด้วยชุดตัวต้านทานและตัวเหนี่ยวนำและแขนอีกข้างประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกัน
เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับใช้เพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่รู้จัก ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของ Maxwell และอีกอันหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน Maxwell
สะพานของ Maxwell ใช้ในการวัดค่าของความเหนี่ยวนำขนาดกลาง circuit diagram ของสะพาน Maxwell แสดงไว้ในรูปด้านล่าง
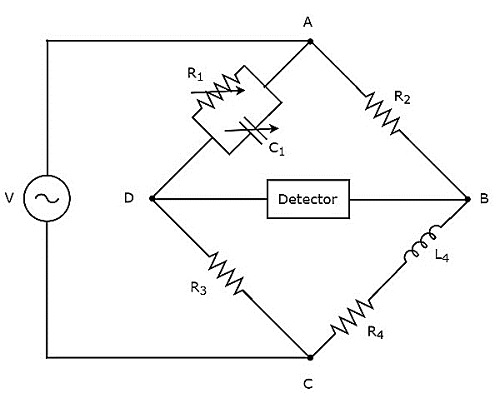
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือสี่เหลี่ยม แขน AB และ CD ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ตามลำดับ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ แขน DA ประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ สมการ 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ สมการ 2
โดยการแทนค่าของตัวต้านทาน $ R_ {1} $, $ R_ {2} $ และ $ R_ {3} $ ในสมการ 1 เราจะได้ค่าตัวต้านทาน $ R_ {4} $ ในทำนองเดียวกันโดยการแทนค่าของตัวเก็บประจุ $ C_ {1} $ และค่าของตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ในสมการ 2 เราจะได้ค่าตัวเหนี่ยวนำ $ L_ {4 } $.
advantage ของสะพานของ Maxwell คือทั้งค่าของตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ จะไม่ขึ้นกับค่าของความถี่
สะพาน Hay
Hay's bridge เป็นบริดจ์รุ่นดัดแปลงของ Maxwell ซึ่งเราได้รับโดยการปรับเปลี่ยนแขนซึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานเข้ากับแขนซึ่งประกอบด้วยชุดตัวต้านทานและตัวเก็บประจุในสะพานของ Maxwell
สะพาน Hay ใช้ในการวัดค่าของความเหนี่ยวนำสูง circuit diagram ของสะพาน Hay แสดงไว้ในรูปด้านล่าง
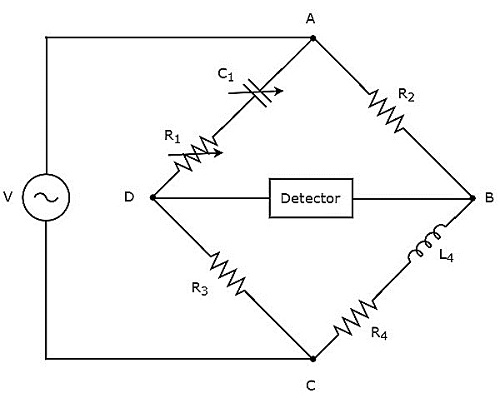
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือสี่เหลี่ยม แขน AB และ CD ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {3} $ ตามลำดับ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเหนี่ยวนำ $ L_ {4} $ แขน DA ประกอบด้วยชุดตัวต้านทาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ โอเมก้า C_ {1}} \ right)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $
คูณตัวเศษและตัวส่วนของเงื่อนไขด้านขวามือของสมการข้างบนด้วย $ 1 - j \ omega R_ {1} C_ {1} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ โอเมก้า R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ โอเมก้า ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ สมการ 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ สมการ 4
โดยการแทนค่าของ $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ และ $ \ omega $ ในสมการ 3 และสมการ 4 เราจะได้ค่าของตัวต้านทาน $ R_ {4 } $ และตัวเหนี่ยวนำ $ L_ {4} $
ในบทที่แล้วเราได้พูดถึงสะพาน AC สองตัวซึ่งสามารถใช้ในการวัดค่าความเหนี่ยวนำได้ ในบทนี้ให้เราพิจารณาเกี่ยวกับสิ่งต่อไปนี้two AC bridges.
- สะพานเชริง
- สะพานของ Wien
สะพานทั้งสองนี้สามารถใช้เพื่อวัดความจุและความถี่ตามลำดับ
สะพานเชริง
สะพานเชริงเป็นสะพานไฟฟ้ากระแสสลับที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shapeซึ่งแขนข้างหนึ่งประกอบด้วยตัวต้านทานเดี่ยวแขนข้างหนึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบอนุกรมแขนข้างหนึ่งประกอบด้วยตัวเก็บประจุตัวเดียวและแขนอีกข้างประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกัน
นอกจากนี้เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับยังใช้เพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่ทราบสาเหตุด้วยเหตุนี้หนึ่งในนั้นจึงถูกวางไว้ในแนวทแยงมุมของสะพาน Schering และอีกตัวหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน Schering
Schering bridge ใช้ในการวัดค่าความจุ circuit diagram ของสะพานเชริงแสดงไว้ในรูปด้านล่าง
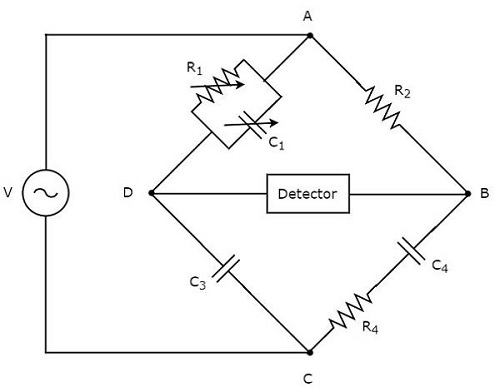
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขน AB ประกอบด้วยตัวต้านทาน $ R_ {2} $ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเก็บประจุ $ C_ {4} $ ซีดีอาร์มประกอบด้วยตัวเก็บประจุ $ C_ {3} $ แขน DA ประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $
$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $
$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $
$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ สมการ 1
$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ สมการ 2
โดยแทนค่าของ $ R_ {1}, R_ {2} $ และ $ C_ {3} $ ในสมการ 1 เราจะได้ค่าของตัวเก็บประจุ $ C_ {4} $ ในทำนองเดียวกันโดยแทนที่ค่าของ $ R_ {2}, C_ {1} $ และ $ C_ {3} $ ในสมการ 2 เราจะได้ค่าตัวต้านทาน $ R_ {4} $
advantage ของสะพาน Schering คือทั้งค่าของตัวต้านทาน $ R_ {4} $ และตัวเก็บประจุ $ C_ {4} $ ไม่ขึ้นกับค่าของความถี่
สะพานของ Wien
Wien’s bridgeเป็นสะพานไฟฟ้ากระแสสลับที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือรูปสี่เหลี่ยมจัตุรัส ในบรรดาแขนสองข้างประกอบด้วยตัวต้านทานตัวเดียวแขนข้างหนึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกันและแขนอีกข้างประกอบด้วยชุดตัวต้านทานและตัวเก็บประจุ
นอกจากนี้ยังต้องใช้เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับเพื่อค้นหาค่าความถี่ ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของ Wien และอีกอันหนึ่งวางไว้ในแนวทแยงมุมของสะพาน Wien
circuit diagram ของสะพานของ Wien แสดงอยู่ในรูปด้านล่าง
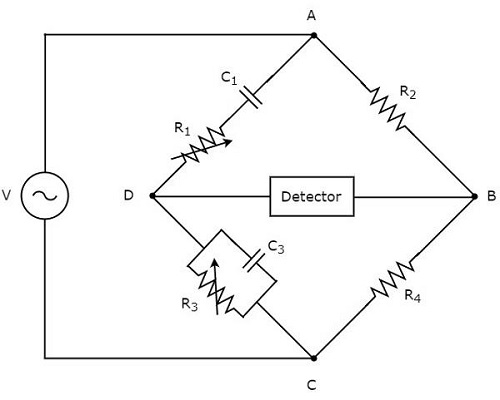
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขน AB และ BC ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {4} $ ตามลำดับ แขนซีดีประกอบด้วยตัวต้านทานแบบขนาน $ R_ {3} $ และตัวเก็บประจุ $ C_ {3} $ แขน DA ประกอบด้วยชุดตัวต้านทาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$
$ Z_ {2} = R_ {2} $
$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$
$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$
$ Z_ {4} = R_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
$$ \ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right) $$
$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3} $
Equate ตามลำดับ real terms ของสมการข้างต้น
$$ R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0 $$
$ \ Rightarrow 1- \ โอเมก้า ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $
$ \ Rightarrow 1 = \ โอเมก้า ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $
$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
Substitute, $ \ omega = 2 \ pi f $ ในสมการด้านบน
$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$
$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
เราสามารถหาค่าความถี่ $ f $ ของแหล่งกำเนิดแรงดันไฟฟ้ากระแสสลับได้โดยการแทนที่ค่า $ R_ {1}, R_ {3}, C_ {1} $ และ $ C_ {3} $ ในสมการข้างบน
ถ้า $ R_ {1} = R_ {3} = R $ และ $ C_ {1} = C_ {3} = C $ เราจะหาค่าความถี่ $ f $ ของแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับได้โดยใช้สูตรต่อไปนี้ .
$$ f = \ frac {1} {2 \ pi RC} $$
สะพาน Wein ส่วนใหญ่ใช้ในการค้นหา frequency value ของช่วง AF
โดยพื้นฐานแล้ว Transducer จะแปลงพลังงานรูปแบบหนึ่งเป็นพลังงานอีกรูปแบบหนึ่ง ทรานสดิวเซอร์ซึ่งแปลงรูปแบบพลังงานที่ไม่ใช่ไฟฟ้าเป็นพลังงานไฟฟ้าเรียกว่าelectrical transducer. block diagram ของตัวแปลงสัญญาณไฟฟ้าแสดงไว้ในรูปด้านล่าง
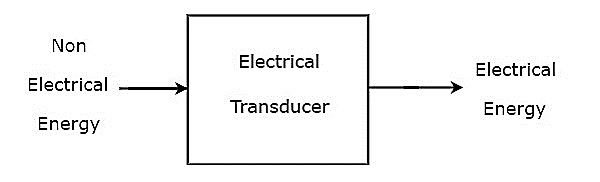
ดังแสดงในรูปตัวแปลงสัญญาณไฟฟ้าจะสร้างเอาต์พุตซึ่งมีพลังงานไฟฟ้า เอาต์พุตของตัวแปลงสัญญาณไฟฟ้าเทียบเท่ากับอินพุตซึ่งมีพลังงานที่ไม่ใช่ไฟฟ้า
ประเภทของตัวแปลงสัญญาณไฟฟ้า
โดยหลักแล้วตัวแปลงสัญญาณไฟฟ้าสามารถแบ่งได้ดังต่อไปนี้ two types.
- ตัวแปลงสัญญาณที่ใช้งานอยู่
- ตัวแปลงสัญญาณแบบพาสซีฟ
ตอนนี้ให้เราพูดคุยเกี่ยวกับทรานสดิวเซอร์สองประเภทนี้สั้น ๆ
ตัวแปลงสัญญาณที่ใช้งานอยู่
ตัวแปลงสัญญาณซึ่งสามารถผลิตปริมาณไฟฟ้าอย่างใดอย่างหนึ่งเช่นแรงดันและกระแสเรียกว่า active transducer. เรียกอีกอย่างว่าตัวแปลงสัญญาณที่สร้างขึ้นเองเนื่องจากไม่ต้องใช้แหล่งจ่ายไฟภายนอก
block diagram ของตัวแปลงสัญญาณที่ใช้งานอยู่แสดงไว้ในรูปด้านล่าง
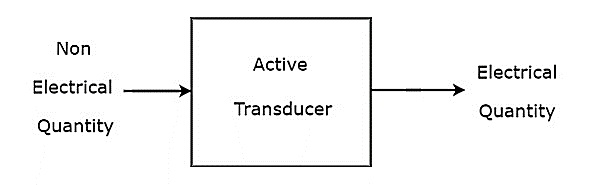
ดังที่แสดงในรูปตัวแปลงสัญญาณที่ใช้งานอยู่จะสร้างปริมาณไฟฟ้า (หรือสัญญาณ) ซึ่งเทียบเท่ากับปริมาณอินพุต (หรือสัญญาณ) ที่ไม่ใช่ไฟฟ้า
Examples
ต่อไปนี้เป็นตัวอย่างของทรานสดิวเซอร์ที่ใช้งานอยู่
- เครื่องแปลงสัญญาณไฟฟ้า Piezo
- เครื่องแปลงสัญญาณไฟฟ้าภาพถ่าย
- เครื่องแปลงสัญญาณไฟฟ้าเทอร์โม
เราจะพูดถึงทรานสดิวเซอร์ที่ใช้งานอยู่เหล่านี้ในบทถัดไป
ตัวแปลงสัญญาณแบบพาสซีฟ
ทรานสดิวเซอร์ซึ่งไม่สามารถผลิตปริมาณไฟฟ้าเช่นแรงดันและกระแสได้เรียกว่า passive transducer. แต่มันก่อให้เกิดการเปลี่ยนแปลงในองค์ประกอบแฝงเช่นตัวต้านทาน (R) ตัวเหนี่ยวนำ (L) และตัวเก็บประจุ (C) ตัวแปลงสัญญาณแบบพาสซีฟต้องใช้แหล่งจ่ายไฟภายนอก
block diagram ของตัวแปลงสัญญาณแบบพาสซีฟแสดงไว้ในรูปด้านล่าง
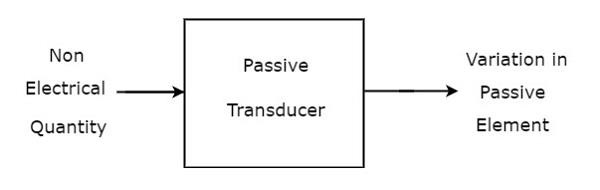
ดังที่แสดงในรูปตัวแปลงสัญญาณแบบพาสซีฟจะสร้างความแปรผันในองค์ประกอบแบบพาสซีฟตามการเปลี่ยนแปลงของปริมาณอินพุตที่ไม่ใช่ไฟฟ้า (หรือสัญญาณ)
Examples
ต่อไปนี้เป็นตัวอย่างของทรานสดิวเซอร์แบบพาสซีฟ
- Resistive Transducer
- ตัวแปลงสัญญาณอุปนัย
- ตัวแปลงสัญญาณ Capacitive
เราจะพูดคุยเกี่ยวกับตัวแปลงสัญญาณแฝงเหล่านี้ในบทต่อ ๆ ไป
Active transducerเป็นตัวแปลงสัญญาณซึ่งแปลงปริมาณที่ไม่ใช่ไฟฟ้าเป็นปริมาณไฟฟ้า ให้เราพิจารณาปริมาณที่ไม่ใช่ไฟฟ้าเช่นความดันการส่องสว่างของแสงและอุณหภูมิ ดังนั้นเราจะได้รับตัวแปลงสัญญาณที่ใช้งานอยู่สามตัวต่อไปนี้ขึ้นอยู่กับปริมาณที่ไม่ใช่ไฟฟ้าที่เราเลือก
- เครื่องแปลงสัญญาณไฟฟ้า Piezo
- เครื่องแปลงสัญญาณไฟฟ้าภาพถ่าย
- เครื่องแปลงสัญญาณไฟฟ้าเทอร์โม
ตอนนี้ให้เราพูดคุยเกี่ยวกับตัวแปลงสัญญาณที่ใช้งานทั้งสามนี้ทีละตัว
เครื่องแปลงสัญญาณไฟฟ้า Piezo
มีการกล่าวถึงตัวแปลงสัญญาณที่ใช้งานอยู่ piezo electric transducerเมื่อมันสร้างปริมาณไฟฟ้าซึ่งเทียบเท่ากับอินพุตแรงดัน สารสามชนิดต่อไปนี้แสดงฤทธิ์ไฟฟ้าแบบเพียโซ
- Quartz
- เกลือ Rochelle
- Tourmaline
ผลกระทบจากไฟฟ้ากระแสไฟฟ้าที่แสดงโดยสารทั้งสามนี้คือเกลือ Tourmaline, Quartz และ Rochelle ตามลำดับจากน้อยไปมาก ลำดับความแข็งแรงเชิงกลจากน้อยไปมากที่มีสารทั้งสามนี้ ได้แก่ เกลือ Rochelle, Quartz, Tourmaline
Quartz ใช้เป็นตัวแปลงสัญญาณไฟฟ้าแบบเพียโซเนื่องจากมีการแสดงผลไฟฟ้าแบบเพีโซปานกลางและมีความแข็งแรงเชิงกลปานกลางระหว่างสารไฟฟ้าเพีโซทั้งสามชนิดนี้
เครื่องแปลงสัญญาณควอตซ์
circuit diagramของตัวแปลงสัญญาณควอตซ์แสดงไว้ในรูปด้านล่าง ดังแสดงในรูปผลึกควอตซ์วางอยู่ระหว่างฐานและสมาชิกผลรวมของแรง สามารถวัดแรงดันไฟฟ้าขาออกผ่านขั้วไฟฟ้าโลหะซึ่งวางอยู่บนผลึกควอตซ์ทั้งสองด้าน
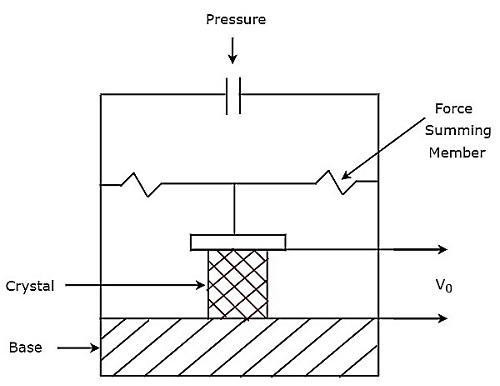
output voltage, $ V_ {0} $ ของตัวแปลงสัญญาณแรงดันสูงกว่าจะเป็น
$$ V_ {0} = \ frac {Q} {C} $$
เครื่องแปลงสัญญาณไฟฟ้าภาพถ่าย
ทรานสดิวเซอร์ที่ใช้งานอยู่กล่าวได้ว่าเป็นตัวแปลงสัญญาณไฟฟ้าภาพถ่ายเมื่อผลิตปริมาณไฟฟ้าซึ่งเทียบเท่ากับการส่องสว่างของอินพุตแสง circuit diagram ของตัวแปลงสัญญาณไฟฟ้าภาพถ่ายแสดงไว้ในรูปด้านล่าง
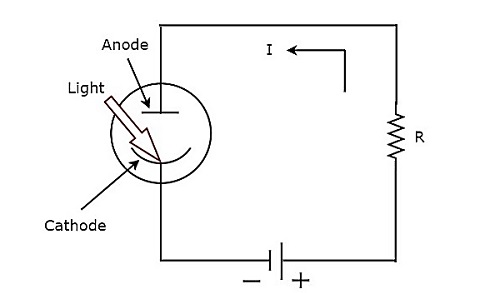
working ของตัวแปลงสัญญาณไฟฟ้าภาพถ่ายมีการระบุไว้ด้านล่าง
Step1 - เครื่องแปลงสัญญาณไฟฟ้าภาพถ่ายจะปล่อยอิเล็กตรอนเมื่อแสงตกบนแคโทดของมัน
Step2 - ตัวแปลงสัญญาณไฟฟ้าภาพถ่ายสร้างกระแส I ในวงจรเนื่องจากแรงดึงดูดของอิเล็กตรอนต่อขั้วบวก
เราสามารถค้นหาไฟล์ sensitivity ของตัวแปลงสัญญาณไฟฟ้าภาพถ่ายโดยใช้สูตรต่อไปนี้
$$ S = \ frac {I} {i} $$
ที่ไหน
$ S $ คือความไวของตัวแปลงสัญญาณไฟฟ้าภาพถ่าย
$ I $ คือกระแสเอาท์พุตของเครื่องแปลงสัญญาณไฟฟ้าภาพถ่าย
$ i $ คือการส่องสว่างของอินพุตแสงของตัวแปลงสัญญาณไฟฟ้าภาพถ่าย
เครื่องแปลงสัญญาณไฟฟ้าเทอร์โม
มีการกล่าวถึงตัวแปลงสัญญาณที่ใช้งานอยู่ thermo electric transducerเมื่อผลิตปริมาณไฟฟ้าซึ่งเทียบเท่ากับอินพุตอุณหภูมิ ทรานสดิวเซอร์สองตัวต่อไปนี้เป็นตัวอย่างของตัวแปลงสัญญาณไฟฟ้าแบบเทอร์โม
- เทอร์มิสเตอร์ทรานสดิวเซอร์
- เทอร์โมคัปเปิลทรานสดิวเซอร์
ตอนนี้ให้เราพูดคุยเกี่ยวกับตัวแปลงสัญญาณสองตัวนี้ทีละตัว
เทอร์มิสเตอร์ทรานสดิวเซอร์
ตัวต้านทานซึ่งขึ้นอยู่กับอุณหภูมิเรียกว่าตัวต้านทานความร้อน เรียกสั้น ๆ ว่าThermistor. ค่าสัมประสิทธิ์อุณหภูมิของเทอร์มิสเตอร์เป็นลบ นั่นหมายความว่าเมื่ออุณหภูมิเพิ่มขึ้นความต้านทานของเทอร์มิสเตอร์จะลดลง
Mathematicallyความสัมพันธ์ระหว่างความต้านทานของเทอร์มิสเตอร์และอุณหภูมิสามารถแสดงเป็น
$$ R_ {1} = R_ {2} e ^ \ left (\ beta \ left [\ frac {1} {T_ {1}} - \ frac {1} {T_ {2}} \ right] \ right) $$
Where,
$ R_ {1} $ คือความต้านทานของเทอร์มิสเตอร์ที่อุณหภูมิ $ {T_ {1}} ^ {0} K $
$ R_ {2} $ คือความต้านทานของเทอร์มิสเตอร์ที่อุณหภูมิ $ {T_ {2}} ^ {0} K $
$ \ beta $ คือค่าคงที่ของอุณหภูมิ
advantage ของทรานซิสเตอร์เทอร์มิสเตอร์คือมันจะให้การตอบสนองที่รวดเร็วและมีเสถียรภาพ
เทอร์โมคัปเปิลทรานสดิวเซอร์
ตัวแปลงสัญญาณเทอร์โมคัปเปิลสร้างแรงดันไฟฟ้าขาออกสำหรับการเปลี่ยนแปลงอุณหภูมิที่สอดคล้องกันที่อินพุต หากลวดสองเส้นของโลหะที่แตกต่างกันถูกรวมเข้าด้วยกันเพื่อสร้างทางแยกสองเส้นจะเรียกการกำหนดค่าทั้งหมดนั้นThermocouple. แผนภาพวงจรของเทอร์โมคัปเปิลพื้นฐานแสดงไว้ด้านล่าง -
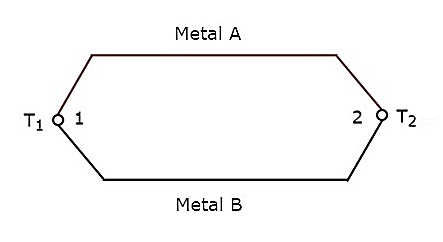
เทอร์โมคัปเปิลข้างต้นมีโลหะสองชนิดคือ A & B และสองจุดเชื่อม 1 & 2 พิจารณาอุณหภูมิอ้างอิงคงที่ $ T_ {2} $ ที่ทางแยก 2 ปล่อยให้อุณหภูมิที่ทางแยก 1 คือ $ T_ {1} $ เทอร์โมคัปเปิลสร้างไฟล์emf (แรงจูงใจทางไฟฟ้า) เมื่อใดก็ตามที่ค่าของ $ T_ {1} $ และ $ T_ {2} $ แตกต่างกัน
นั่นหมายความว่าเทอร์โมคัปเปิลจะสร้างแรงเคลื่อนไฟฟ้าเมื่อใดก็ตามที่มีความแตกต่างของอุณหภูมิระหว่างจุดแยกทั้งสอง 1 และ 2 และเป็นสัดส่วนโดยตรงกับความแตกต่างของอุณหภูมิระหว่างทางแยกทั้งสอง Mathematicallyสามารถแสดงเป็น
$$ e \ alpha \ left (T_ {1} -T_ {2} \ right) $$
ที่ไหน
$ e $ คือแรงเคลื่อนไฟฟ้าที่สร้างโดยเทอร์โมคัปเปิล
วงจรเทอร์โมคัปเปิลด้านบนสามารถแสดงได้ดังแสดงในรูปด้านล่างสำหรับการใช้งานจริง
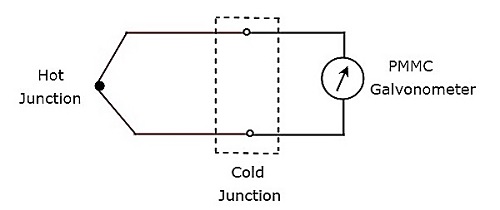
ส่วนของวงจรซึ่งอยู่ระหว่างทางแยกร้อนและเย็นรวมทั้งทางแยกทั้งสองนั้นเป็นแบบจำลองเทอร์โมคัปเปิลพื้นฐานที่เทียบเท่ากัน กัลวาโนมิเตอร์ PMMC เชื่อมต่อผ่านทางแยกเย็นและจะเบี่ยงเบนไปตามแรงเคลื่อนไฟฟ้าที่สร้างขึ้นผ่านทางแยกเย็นThermocouple transducer เป็นตัวแปลงสัญญาณเทอร์โมอิเล็กทริกที่ใช้กันมากที่สุด
passive transducerเป็นตัวแปลงสัญญาณซึ่งทำให้เกิดการเปลี่ยนแปลงในองค์ประกอบแบบพาสซีฟ เราจะพิจารณาองค์ประกอบแบบพาสซีฟเช่นตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุ ดังนั้นเราจะได้รับตัวแปลงสัญญาณแบบพาสซีฟสามตัวต่อไปนี้ขึ้นอยู่กับองค์ประกอบแฝงที่เราเลือก
- Resistive Transducer
- ตัวแปลงสัญญาณอุปนัย
- ตัวแปลงสัญญาณ Capacitive
ตอนนี้ให้เราพูดคุยเกี่ยวกับตัวแปลงสัญญาณแบบพาสซีฟสามตัวนี้ทีละตัว
Resistive Transducer
ตัวแปลงสัญญาณแบบพาสซีฟกล่าวว่าเป็น resistive transducerเมื่อมันก่อให้เกิดการเปลี่ยนแปลง (เปลี่ยนแปลง) ในค่าความต้านทาน สูตรต่อไปนี้สำหรับresistance, R ของตัวนำโลหะ
$$ R = \ frac {\ rho \: l} {A} $$
ที่ไหน
$ \ rho $ คือความต้านทานของตัวนำ
$ l $ คือความยาวของตัวนำ
$ A $ คือพื้นที่หน้าตัดของตัวนำ
ค่าความต้านทานขึ้นอยู่กับพารามิเตอร์สามตัว $ \ rho, l $ & $ A $ ดังนั้นเราสามารถสร้างไฟล์resistive transducersขึ้นอยู่กับรูปแบบของหนึ่งในสามพารามิเตอร์ $ \ rho, l $ & $ A $ ความแปรผันของพารามิเตอร์ใดพารามิเตอร์หนึ่งในสามตัวนั้นจะเปลี่ยนค่าความต้านทาน
ความต้านทาน R เป็นสัดส่วนโดยตรงกับ resistivityของตัวนำ $ \ rho $. ดังนั้นเมื่อความต้านทานของตัวนำ $ \ rho $ เพิ่มค่าความต้านทาน R ก็เพิ่มขึ้นด้วย ในทำนองเดียวกันเมื่อความต้านทานของตัวนำ $ \ rho $ ลดค่าความต้านทาน R ก็จะลดลงด้วย
ความต้านทาน R เป็นสัดส่วนโดยตรงกับ lengthของตัวนำ $ l $. ดังนั้นเมื่อความยาวของตัวนำ $ l $ เพิ่มค่าความต้านทาน R ก็เพิ่มขึ้นด้วย ในทำนองเดียวกันเมื่อความยาวของตัวนำ $ l $ ลดค่าความต้านทาน R ก็จะลดลงด้วย
ความต้านทาน R เป็นสัดส่วนผกผันกับ cross sectional areaของผู้ดำเนินรายการ $ A $. ดังนั้นเมื่อพื้นที่หน้าตัดของตัวนำ $ A $ จะเพิ่มค่าความต้านทาน R จะลดลง ในทำนองเดียวกันเมื่อพื้นที่หน้าตัดของตัวนำ $ A $ ลดค่าความต้านทาน R จะเพิ่มขึ้น
ตัวแปลงสัญญาณอุปนัย
ตัวแปลงสัญญาณแบบพาสซีฟกล่าวว่าเป็น inductive transducerเมื่อมันก่อให้เกิดการเปลี่ยนแปลง (เปลี่ยนแปลง) ในค่าความเหนี่ยวนำ สูตรต่อไปนี้สำหรับinductance, L ของตัวเหนี่ยวนำ
$ L = \ frac {N ^ {2}} {S} $ สมการ 1
ที่ไหน
$ N $ คือจำนวนรอบของขดลวด
$ S $ คือจำนวนรอบของขดลวด
สูตรต่อไปนี้สำหรับ reluctance, S ของขดลวด
$ S = \ frac {l} {\ mu A} $ สมการ 2
ที่ไหน
$ l $ คือความยาวของวงจรแม่เหล็ก
$ \ mu $ คือการซึมผ่านของแกน
$ A $ คือพื้นที่ของวงจรแม่เหล็กที่ฟลักซ์ไหล
แทนสมการ 2 ในสมการ 1
$$ L = \ frac {N ^ {2}} {\ left (\ frac {l} {\ mu A} \ right)} $$
$ \ Rightarrow L = \ frac {N ^ {2} \ mu A} {l} $ สมการ 3
จากสมการ 1 และสมการ 3 เราสามารถสรุปได้ว่าค่าความเหนี่ยวนำขึ้นอยู่กับพารามิเตอร์สามตัว $ N, S $ & $ \ mu $ ดังนั้นเราสามารถสร้างไฟล์inductive transducersขึ้นอยู่กับรูปแบบของหนึ่งในสามพารามิเตอร์ $ N, S $ & $ \ mu $ เนื่องจากความแปรผันของพารามิเตอร์ใดพารามิเตอร์หนึ่งในสามตัวนั้นจึงเปลี่ยนค่าความเหนี่ยวนำ
ตัวเหนี่ยวนำ L เป็นสัดส่วนโดยตรงกับกำลังสองของ number of turns of coil. ดังนั้นเมื่อจำนวนรอบของขดลวด $ N $ เพิ่มมูลค่าของการเหนี่ยวนำ $ L $ ก็เพิ่มขึ้นด้วย ในทำนองเดียวกันเมื่อจำนวนรอบของขดลวด $ N $ ลดค่าของการเหนี่ยวนำ $ L $ ก็ลดลงเช่นกัน
ตัวเหนี่ยวนำ $ L $ แปรผกผันกับ reluctance of coil, $ S $. ดังนั้นเนื่องจากความไม่เต็มใจของขดลวด $ S $ จะเพิ่มมูลค่าของการเหนี่ยวนำ $ L $ จะลดลง ในทำนองเดียวกันเมื่อไม่เต็มใจขดลวด $ S $ จะลดค่าของการเหนี่ยวนำ $ L $ เพิ่มขึ้น
ตัวเหนี่ยวนำ L เป็นสัดส่วนโดยตรงกับ permeability of core, $ \ mu $. ดังนั้นเมื่อการซึมผ่านของแกน $ \ mu $ จะเพิ่มมูลค่าของการเหนี่ยวนำ L ก็เพิ่มขึ้นด้วย ในทำนองเดียวกันการซึมผ่านของแกน $ \ mu $ จะลดค่าของการเหนี่ยวนำ L ก็จะลดลงด้วยเช่นกัน
ตัวแปลงสัญญาณ Capacitive
ตัวแปลงสัญญาณแบบพาสซีฟกล่าวว่าเป็น capacitive transducerเมื่อมันก่อให้เกิดการเปลี่ยนแปลง (เปลี่ยนแปลง) ในค่าความจุ สูตรต่อไปนี้สำหรับcapacitance, C ของตัวเก็บประจุแบบแผ่นขนาน
$$ C = \ frac {\ varepsilon A} {d} $$
ที่ไหน
$ \ varepsilon $ คือการอนุญาตหรือค่าคงที่ไดอิเล็กทริก
$ A $ คือพื้นที่สองแผ่นที่มีประสิทธิภาพ
$ d $ คือพื้นที่ที่มีประสิทธิภาพของสองแผ่น
ค่าความจุขึ้นอยู่กับพารามิเตอร์สามตัว $ \ varepsilon, A $ & $ d $ ดังนั้นเราสามารถสร้างไฟล์capacitive transducersขึ้นอยู่กับการเปลี่ยนแปลงในหนึ่งในสามพารามิเตอร์ $ \ varepsilon, A $ & $ d $ เนื่องจากความแปรผันของพารามิเตอร์ใดพารามิเตอร์หนึ่งในสามตัวนั้นจึงเปลี่ยนค่าความจุ
ความจุ C เป็นสัดส่วนโดยตรงกับ permittivity, $ \ varepsilon $. ดังนั้นเมื่ออนุญาต $ \ varepsilon $ จึงเพิ่มมูลค่าของความจุ C ก็เพิ่มขึ้นด้วย ในทำนองเดียวกันการอนุญาต $ \ varepsilon $ จะลดค่าของความจุ C ก็จะลดลงเช่นกัน
ความจุ C เป็นสัดส่วนโดยตรงกับ effective area of two plates, $ ก $. ดังนั้นเมื่อพื้นที่สองแผ่นมีประสิทธิภาพ $ A $ จะเพิ่มมูลค่าของความจุ C ก็จะเพิ่มขึ้นด้วย ในทำนองเดียวกันเนื่องจากพื้นที่ที่มีประสิทธิภาพของแผ่นสองแผ่น $ A $ จะลดค่าของความจุ C ก็จะลดลงเช่นกัน
ความจุ C เป็นสัดส่วนผกผันกับ distance between two plates, $ d $. ดังนั้นเมื่อระยะห่างระหว่างแผ่นสองแผ่น $ d $ จะเพิ่มมูลค่าของความจุ C จะลดลง ในทำนองเดียวกันเมื่อระยะห่างระหว่างแผ่นสองแผ่น $ d $ จะลดค่าความจุ C จะเพิ่มขึ้น
ในบทนี้เราได้พูดถึงตัวแปลงสัญญาณแบบพาสซีฟสามตัว ในบทถัดไปให้เราพูดถึงตัวอย่างของตัวแปลงสัญญาณแบบพาสซีฟแต่ละตัว
physical quantitiesเช่นการกระจัดความเร็วแรงอุณหภูมิและอื่น ๆ ล้วนเป็นปริมาณที่ไม่ใช่ไฟฟ้า ตัวแปลงสัญญาณที่ใช้งานอยู่จะแปลงปริมาณทางกายภาพเป็นสัญญาณไฟฟ้า ในขณะที่ตัวแปลงสัญญาณแบบพาสซีฟจะแปลงปริมาณทางกายภาพเป็นรูปแบบในองค์ประกอบแฝง
ดังนั้นตามข้อกำหนดเราสามารถเลือกตัวแปลงสัญญาณที่ใช้งานอยู่หรือตัวแปลงสัญญาณแบบพาสซีฟ ในบทนี้ให้เราพูดถึงวิธีการวัดการกระจัดโดยใช้ตัวแปลงสัญญาณแบบพาสซีฟ ถ้าร่างกายที่เคลื่อนที่จากจุดหนึ่งไปยังอีกจุดหนึ่งเป็นเส้นตรงความยาวระหว่างจุดทั้งสองนั้นจะเรียกว่าdisplacement.
เรามีดังต่อไปนี้ three passive transducers
- Resistive Transducer
- ตัวแปลงสัญญาณอุปนัย
- ตัวแปลงสัญญาณ Capacitive
ตอนนี้ให้เราพูดคุยเกี่ยวกับการวัดการกระจัดด้วยตัวแปลงสัญญาณพาสซีฟสามตัวนี้ทีละตัว
การวัดการกระจัดโดยใช้ Resistive Transducer
circuit diagram ของตัวแปลงสัญญาณตัวต้านทานซึ่งใช้ในการวัดการกระจัดแสดงไว้ในรูปด้านล่าง
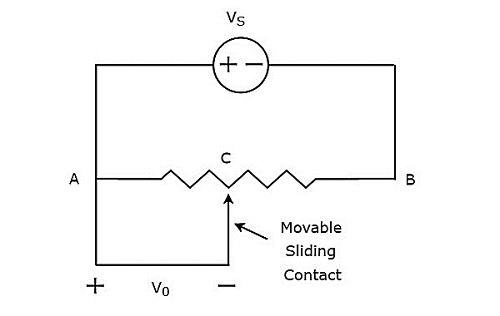
วงจรข้างต้นประกอบด้วยโพเทนชิออมิเตอร์และแหล่งจ่ายแรงดัน $ V_ {S} $ เราสามารถพูดได้ว่าทั้งสองเชื่อมต่อแบบขนานกับจุด A & B โพเทนชิออมิเตอร์มีหน้าสัมผัสแบบเลื่อนซึ่งสามารถเปลี่ยนแปลงได้ ดังนั้นจุด C จึงเป็นตัวแปรหนึ่ง ในวงจรด้านบนไฟล์output voltage, $ V_ {0} $ ถูกวัดจากจุด A & C
Mathematicallyความสัมพันธ์ระหว่างแรงดันไฟฟ้าและระยะทางสามารถแสดงเป็น
$$ \ frac {V_ {0}} {V_ {S}} = \ frac {AC} {AB} $$
ดังนั้นเราควรเชื่อมต่อร่างกายที่จะวัดการกระจัดกับหน้าสัมผัสบานเลื่อน ดังนั้นเมื่อใดก็ตามที่ร่างกายเคลื่อนไหวเป็นเส้นตรงจุด C ก็แตกต่างกันไปเช่นกัน ด้วยเหตุนี้แรงดันไฟฟ้าขาออก $ V_ {0} $ จึงเปลี่ยนแปลงตามไปด้วย
ในกรณีนี้เราสามารถหาการกระจัดได้โดยการวัดแรงดันขาออก $ V_ {0} $
การวัดการกระจัดโดยใช้ตัวแปลงสัญญาณอุปนัย
circuit diagram ของตัวแปลงสัญญาณอุปนัยซึ่งใช้ในการวัดการกระจัดแสดงไว้ในรูปด้านล่าง
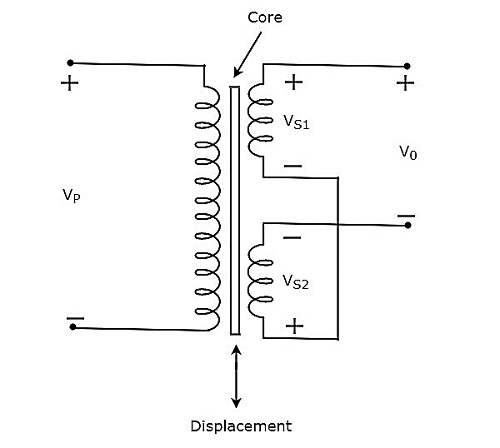
หม้อแปลงที่อยู่ในวงจรด้านบนมีขดลวดปฐมภูมิและขดลวดทุติยภูมิสองเส้น ที่นี่จุดสิ้นสุดของขดลวดทุติยภูมิสองเส้นจะรวมเข้าด้วยกัน ดังนั้นเราสามารถพูดได้ว่าขดลวดทุติยภูมิทั้งสองนี้เชื่อมต่อกันseries opposition.
แรงดันไฟฟ้า $ V_ {P} $ ถูกนำไปใช้กับขดลวดปฐมภูมิของหม้อแปลง ให้แรงดันไฟฟ้าที่พัฒนาขึ้นสำหรับขดลวดทุติยภูมิแต่ละอันคือð ?? '‰ð ??' † 1 และð ?? '‰ð ??' † 2. แรงดันไฟฟ้าขาออก $ V_ {0} $ จะถูกนำข้ามจุดเริ่มต้นของขดลวดทุติยภูมิสองขดลวด
Mathematically, แรงดันขาออก, ð ?? '‰ 0 สามารถเขียนเป็น
$$ V_ {0} = V_ {S1} -V_ {S2} $$
เรียกว่าหม้อแปลงที่อยู่ในวงจรด้านบน differential transformerเนื่องจากมันสร้างแรงดันไฟฟ้าขาออกซึ่งเป็นความแตกต่างระหว่าง $ V_ {S1} $ และ $ V_ {S2} $
หากแกนอยู่ที่ตำแหน่งกลางแรงดันขาออก $ V_ {0} $ จะเท่ากับศูนย์ เนื่องจากขนาดและเฟสของ $ V_ {S1} $ และ $ V_ {S2} $ นั้นเท่ากัน
หากแกนกลางไม่อยู่ที่ตำแหน่งกลางแรงดันเอาต์พุต $ V_ {0} $ จะมีขนาดและเฟส เนื่องจากขนาดและเฟสของ $ V_ {S1} $ และ $ V_ {S2} $ จึงไม่เท่ากัน
ดังนั้นเราควรเชื่อมต่อร่างกายที่จะวัดการกระจัดกับแกนกลาง ดังนั้นเมื่อใดก็ตามที่ร่างกายเคลื่อนไหวเป็นเส้นตรงตำแหน่งกลางของแกนกลางจะแตกต่างกันไป ด้วยเหตุนี้แรงดันไฟฟ้าขาออก $ V_ {0} $ จึงเปลี่ยนแปลงตามไปด้วย
ในกรณีนี้เราสามารถค้นหาไฟล์ displacementโดยการวัดแรงดันขาออก $ V_ {0} $ ขนาดและเฟสของแรงดันเอาต์พุต $ V_ {0} $ แสดงถึงการกระจัดของร่างกายและทิศทางตามลำดับ
การวัดการกระจัดโดยใช้ Capacitive Transducer
circuit diagram ของตัวแปลงสัญญาณคาปาซิทีฟซึ่งใช้ในการวัดการกระจัดแสดงไว้ในรูปด้านล่าง
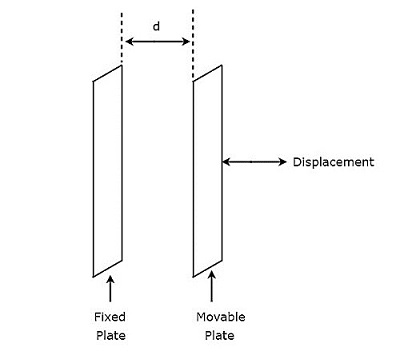
capacitorซึ่งมีอยู่ในวงจรด้านบนมีแผ่นขนานสองแผ่น ในนั้นแผ่นหนึ่งได้รับการแก้ไขและอีกแผ่นหนึ่งเป็นแผ่นที่เคลื่อนย้ายได้ ด้วยเหตุนี้ระยะห่างระหว่างจานทั้งสองนี้ก็จะแตกต่างกันไปด้วย ค่าของความจุจะเปลี่ยนไปเมื่อระยะห่างระหว่างแผ่นตัวเก็บประจุสองแผ่นเปลี่ยนไป
ดังนั้นเราจึงควรเชื่อมต่อร่างกายที่ displacementจะต้องวัดกับแผ่นที่เคลื่อนย้ายได้ของตัวเก็บประจุ ดังนั้นเมื่อใดก็ตามที่ร่างกายเคลื่อนที่เป็นเส้นตรงระยะห่างระหว่างแผ่นตัวเก็บประจุทั้งสองจะแตกต่างกันไป ด้วยเหตุนี้ค่าความจุจึงเปลี่ยนไป
ระบบที่ใช้ในการเก็บข้อมูลเรียกว่า data acquisition systems. ระบบเก็บข้อมูลเหล่านี้จะดำเนินการเช่นการแปลงข้อมูลการจัดเก็บข้อมูลการส่งข้อมูลและการประมวลผลข้อมูล
ระบบรับข้อมูลพิจารณาสิ่งต่อไปนี้ analog signals.
สัญญาณอนาล็อกซึ่งได้มาจากการวัดปริมาณทางไฟฟ้าโดยตรงเช่นแรงดันไฟฟ้า DC และ AC กระแส DC และ AC ความต้านทานและอื่น ๆ
สัญญาณอนาล็อกซึ่งได้รับจากทรานสดิวเซอร์เช่น LVDT เทอร์โมคัปเปิลและอื่น ๆ
ประเภทของระบบการได้มาซึ่งข้อมูล
ระบบการเก็บข้อมูลสามารถแบ่งออกได้ดังต่อไปนี้ two types.
- ระบบการเก็บข้อมูลแบบอะนาล็อก
- ระบบเก็บข้อมูลดิจิทัล
ตอนนี้ให้เราพูดคุยเกี่ยวกับระบบการเก็บข้อมูลสองประเภทนี้ทีละประเภท
ระบบการเก็บข้อมูลแบบอะนาล็อก
ระบบเก็บข้อมูลซึ่งสามารถทำงานด้วยสัญญาณแอนะล็อกเรียกว่า analog data acquisition systems. ต่อไปนี้เป็นบล็อกของระบบรับข้อมูลอนาล็อก
Transducer - แปลงปริมาณทางกายภาพเป็นสัญญาณไฟฟ้า
Signal conditioner - ทำหน้าที่เช่นการขยายสัญญาณและการเลือกส่วนที่ต้องการของสัญญาณ
Display device - แสดงสัญญาณอินพุตเพื่อการตรวจสอบ
Graphic recording instruments - สิ่งเหล่านี้สามารถใช้เพื่อบันทึกข้อมูลอินพุตได้อย่างถาวร
Magnetic tape instrumentation - ใช้สำหรับรับจัดเก็บและทำซ้ำข้อมูลอินพุต
ระบบเก็บข้อมูลดิจิทัล
ระบบการเก็บข้อมูลซึ่งสามารถดำเนินการด้วยสัญญาณดิจิทัลเรียกว่า digital data acquisition systems. ดังนั้นจึงใช้ส่วนประกอบดิจิทัลในการจัดเก็บหรือแสดงข้อมูล
ส่วนใหญ่ดังต่อไปนี้ operations เกิดขึ้นในการรับข้อมูลดิจิทัล
- การได้มาซึ่งสัญญาณอนาล็อก
- การแปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัลหรือข้อมูลดิจิทัล
- การประมวลผลสัญญาณดิจิทัลหรือข้อมูลดิจิทัล
ต่อไปนี้เป็นบล็อกของ Digital data acquisition systems.
Transducer - แปลงปริมาณทางกายภาพเป็นสัญญาณไฟฟ้า
Signal conditioner - ทำหน้าที่เช่นการขยายสัญญาณและการเลือกส่วนที่ต้องการของสัญญาณ
Multiplexer- เชื่อมต่อหนึ่งในหลายอินพุตเพื่อเอาท์พุท ดังนั้นจึงทำหน้าที่ขนานกับตัวแปลงอนุกรม
Analog to Digital Converter - แปลงอินพุตอะนาล็อกเป็นเอาต์พุตดิจิตอลที่เทียบเท่ากัน
Display device - แสดงข้อมูลในรูปแบบดิจิทัล
Digital Recorder - ใช้บันทึกข้อมูลในรูปแบบดิจิทัล
ระบบการเก็บข้อมูลถูกนำมาใช้ในงานต่างๆเช่นชีวการแพทย์และอวกาศ ดังนั้นเราจึงสามารถเลือกระบบเก็บข้อมูลแบบอะนาล็อกหรือระบบเก็บข้อมูลดิจิทัลตามความต้องการ