ตัวเลข Lissajous

Lissajous figureคือรูปแบบที่แสดงบนหน้าจอเมื่อใช้สัญญาณไซน์กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO รูปแบบเหล่านี้จะแตกต่างกันไปตามแอมพลิจูดความถี่และความแตกต่างของเฟสของสัญญาณไซน์ซึ่งใช้กับแผ่นโก่งในแนวนอนและแนวตั้งของ CRO

รูปต่อไปนี้แสดงไฟล์ example ของร่าง Lissajous

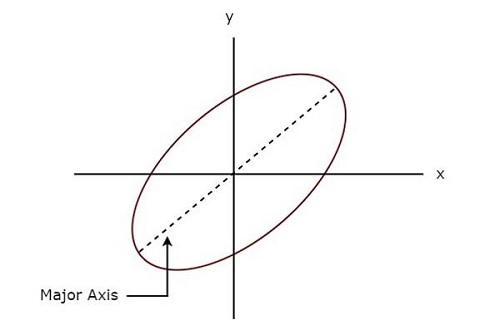
ร่าง Lissajous ด้านบนอยู่ใน elliptical shape และแกนหลักของมันมีมุมเอียงกับแกน x ที่เป็นบวก

การวัดโดยใช้ Lissajous Figures

เราสามารถทำได้ดังต่อไปนี้ two measurements จากร่าง Lissajous

• ความถี่ของสัญญาณไซน์
• ความแตกต่างของเฟสระหว่างสัญญาณไซน์สองตัว

ตอนนี้ให้เราพูดคุยเกี่ยวกับการวัดทั้งสองนี้ทีละรายการ

การวัดความถี่

รูปลิสซาจัสจะแสดงบนหน้าจอเมื่อสัญญาณไซน์ถูกนำไปใช้กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO ดังนั้นใช้สัญญาณไซน์ซึ่งมีมาตรฐานknown frequencyไปยังแผ่นโก่งแนวนอนของ CRO ในทำนองเดียวกันให้ใช้สัญญาณรูปซายน์ซึ่งfrequency คือ unknown ไปยังแผ่นโก่งในแนวตั้งของ CRO

ให้ $ f_ {H} $ และ $ f_ {V} $ เป็นความถี่ของสัญญาณไซน์ซึ่งใช้กับแผ่นเบี่ยงเบนแนวนอนและแนวตั้งของ CRO ตามลำดับ ความสัมพันธ์ระหว่าง $ f_ {H} $ และ $ f_ {V} $ สามารถเป็นได้mathematically แสดงเป็นด้านล่าง

$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$

จากความสัมพันธ์ข้างต้นเราจะได้ความถี่ของสัญญาณไซน์ซึ่งนำไปใช้กับแผ่นโก่งในแนวตั้งของ CRO เป็น

$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (สมการ 1)

ที่ไหน

$ n_ {H} $ คือจำนวนของเส้นสัมผัสแนวนอน

$ n_ {V} $ คือจำนวนของเส้นสัมผัสแนวตั้ง

เราสามารถหาค่าของ $ n_ {H} $ และ $ n_ {V} $ ได้จากรูป Lissajous ดังนั้นโดยการแทนที่ค่าของ $ n_ {H} $, $ n_ {V} $ และ $ f_ {H} $ ในสมการ 1 เราจะได้ค่าของ$f_{V}$กล่าวคือ frequency of sinusoidal signal ที่ใช้กับแผ่นโก่งในแนวตั้งของ CRO

การวัดความแตกต่างของเฟส

รูปลิสซาจัสจะปรากฏบนหน้าจอเมื่อใช้สัญญาณไซน์กับแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO ดังนั้นใช้สัญญาณไซน์ซึ่งมีsame amplitude and frequency ไปยังแผ่นโก่งทั้งแนวนอนและแนวตั้งของ CRO

สำหรับตัวเลข Lissajous เพียงไม่กี่ตัวตามรูปร่างเราสามารถบอกความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองได้โดยตรง

• ถ้าร่าง Lissajous เป็น straight line โดยมีความเอียง $ 45 ^ {\ circ} $ พร้อมแกน x ที่เป็นค่าบวกจากนั้น phase differenceระหว่างสัญญาณไซน์ทั้งสองจะเท่ากับ $ 0 ^ {\ circ} $ นั่นหมายความว่าไม่มีความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองนี้

• ถ้าร่าง Lissajous เป็น straight line โดยมีค่าเอียง $ 135 ^ {\ circ} $ พร้อมแกน x บวกตามด้วย phase differenceระหว่างสัญญาณไซน์ทั้งสองจะเท่ากับ $ 180 ^ {\ circ} $ นั่นหมายความว่าสัญญาณไซน์ทั้งสองนี้อยู่นอกเฟส

• ถ้าร่าง Lissajous อยู่ใน circular shapeดังนั้นความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น $ 90 ^ {\ circ} $ หรือ $ 270 ^ {\ circ} $

เราสามารถคำนวณความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองได้โดยใช้สูตรเมื่อมีตัวเลขลิสซาจัส elliptical shape.

• ถ้าแกนหลักของรูปทรงรีรูปลิสซาจัสที่มีมุมเอียงอยู่ระหว่าง $ 0 ^ {\ circ} $ และ $ 90 ^ {\ circ} $ กับแกน x บวกความแตกต่างเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น

$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$

• ถ้าแกนหลักของรูปทรงรีรูปลิสซาจัสที่มีมุมเอียงอยู่ระหว่าง $ 90 ^ {\ circ} $ และ $ 180 ^ {\ circ} $ กับแกน x ที่เป็นบวกความแตกต่างของเฟสระหว่างสัญญาณไซน์ทั้งสองจะเป็น

$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$

Where,

$ x_ {1} $ คือระยะทางจากจุดเริ่มต้นถึงจุดบนแกน x โดยที่รูปลิสซาจัสรูปวงรีตัดกัน

$ x_ {2} $ คือระยะห่างจากจุดเริ่มต้นถึงเส้นสัมผัสแนวตั้งของรูปทรงรีรูปลิสซาจัส

$ y_ {1} $ คือระยะทางจากจุดกำเนิดถึงจุดบนแกน y โดยที่รูปลิสซาจัสรูปวงรีตัดกัน

$ y_ {2} $ คือระยะทางจากจุดเริ่มต้นถึงเส้นสัมผัสแนวนอนของรูปทรงรีรูปลิสซาจัส

ในบทนี้จะอธิบายถึงวิธีการหาความถี่ของสัญญาณไซน์ที่ไม่ทราบสาเหตุและความแตกต่างของเฟสระหว่างสัญญาณไซน์สองตัวจากตัวเลขลิสซาจัสโดยใช้สูตร