สะพาน AC อื่น ๆ
ในบทที่แล้วเราได้พูดถึงสะพาน AC สองตัวซึ่งสามารถใช้ในการวัดค่าความเหนี่ยวนำได้ ในบทนี้ให้เราพิจารณาเกี่ยวกับสิ่งต่อไปนี้two AC bridges.
- สะพานเชริง
- สะพานของ Wien
สะพานทั้งสองนี้สามารถใช้เพื่อวัดความจุและความถี่ตามลำดับ
สะพานเชริง
สะพานเชริงเป็นสะพานไฟฟ้ากระแสสลับที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shapeซึ่งแขนข้างหนึ่งประกอบด้วยตัวต้านทานเดี่ยวแขนข้างหนึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบอนุกรมแขนข้างหนึ่งประกอบด้วยตัวเก็บประจุตัวเดียวและแขนอีกข้างประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกัน
นอกจากนี้เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับยังใช้เพื่อค้นหาค่าของอิมพีแดนซ์ที่ไม่ทราบสาเหตุด้วยเหตุนี้หนึ่งในนั้นจึงถูกวางไว้ในแนวทแยงมุมของสะพาน Schering และอีกตัวหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน Schering
Schering bridge ใช้ในการวัดค่าความจุ circuit diagram ของสะพานเชริงแสดงไว้ในรูปด้านล่าง
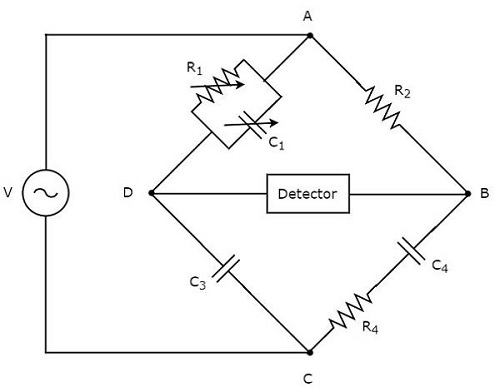
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขน AB ประกอบด้วยตัวต้านทาน $ R_ {2} $ แขน BC ประกอบด้วยชุดตัวต้านทาน $ R_ {4} $ และตัวเก็บประจุ $ C_ {4} $ ซีดีอาร์มประกอบด้วยตัวเก็บประจุ $ C_ {3} $ แขน DA ประกอบด้วยตัวต้านทานแบบขนาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $
$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $
$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $
$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}} $
$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $
โดย comparing เราจะได้เงื่อนไขจริงและจินตภาพของสมการข้างต้น
$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ สมการ 1
$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ สมการ 2
โดยแทนค่าของ $ R_ {1}, R_ {2} $ และ $ C_ {3} $ ในสมการ 1 เราจะได้ค่าของตัวเก็บประจุ $ C_ {4} $ ในทำนองเดียวกันโดยแทนที่ค่าของ $ R_ {2}, C_ {1} $ และ $ C_ {3} $ ในสมการ 2 เราจะได้ค่าตัวต้านทาน $ R_ {4} $
advantage ของสะพาน Schering คือทั้งค่าของตัวต้านทาน $ R_ {4} $ และตัวเก็บประจุ $ C_ {4} $ ไม่ขึ้นกับค่าของความถี่
สะพานของ Wien
Wien’s bridgeเป็นสะพานไฟฟ้ากระแสสลับที่มีแขนทั้งสี่ข้างซึ่งเชื่อมต่อกันในรูปของรูปสี่เหลี่ยมขนมเปียกปูนหรือสี่เหลี่ยม ในบรรดาแขนสองข้างประกอบด้วยตัวต้านทานเดี่ยวแขนข้างหนึ่งประกอบด้วยตัวต้านทานและตัวเก็บประจุแบบขนานกันและแขนอีกข้างประกอบด้วยชุดตัวต้านทานและตัวเก็บประจุ
นอกจากนี้ยังจำเป็นต้องใช้เครื่องตรวจจับ AC และแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับเพื่อค้นหาค่าความถี่ ดังนั้นหนึ่งในสองตัวนี้จึงถูกวางไว้ในแนวทแยงมุมของสะพานของ Wien และอีกอันหนึ่งวางอยู่ในแนวทแยงมุมของสะพาน Wien
circuit diagram ของสะพานของ Wien แสดงอยู่ในรูปด้านล่าง
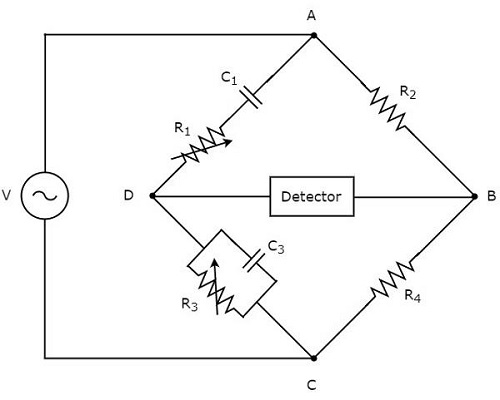
ในวงจรข้างต้นแขน AB, BC, CD และ DA รวมกันเป็นรูปสี่เหลี่ยมขนมเปียกปูนหรือ square shape. แขน AB และ BC ประกอบด้วยตัวต้านทาน $ R_ {2} $ และ $ R_ {4} $ ตามลำดับ แขนซีดีประกอบด้วยตัวต้านทานแบบขนาน $ R_ {3} $ และตัวเก็บประจุ $ C_ {3} $ แขน DA ประกอบด้วยชุดตัวต้านทาน $ R_ {1} $ และตัวเก็บประจุ $ C_ {1} $
ให้ $ Z_ {1}, Z_ {2}, Z_ {3} $ และ $ Z_ {4} $ เป็นอิมพีแดนซ์ของแขน DA, AB, CD และ BC ตามลำดับ values of these impedances จะ
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$
$ Z_ {2} = R_ {2} $
$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$
$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$
$ Z_ {4} = R_ {4} $
Substitute ค่าอิมพีแดนซ์เหล่านี้ในสภาวะสมดุลของสะพาน AC ต่อไปนี้
$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$
$$ \ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right) $$
$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $
$ \ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3} $
Equate ตามลำดับ real terms ของสมการข้างต้น
$$ R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0 $$
$ \ Rightarrow 1- \ โอเมก้า ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $
$ \ Rightarrow 1 = \ โอเมก้า ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $
$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
Substitute, $ \ omega = 2 \ pi f $ ในสมการด้านบน
$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$
$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $
เราสามารถหาค่าความถี่ $ f $ ของแหล่งกำเนิดแรงดันไฟฟ้ากระแสสลับได้โดยแทนที่ค่าของ $ R_ {1}, R_ {3}, C_ {1} $ และ $ C_ {3} $ ในสมการข้างบน
ถ้า $ R_ {1} = R_ {3} = R $ และ $ C_ {1} = C_ {3} = C $ เราจะหาค่าความถี่ $ f $ ของแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับได้โดยใช้สูตรต่อไปนี้ .
$$ f = \ frac {1} {2 \ pi RC} $$
สะพาน Wein ส่วนใหญ่ใช้ในการค้นหา frequency value ของช่วง AF