ทฤษฎีกราฟ - การระบายสี
การระบายสีกราฟไม่ได้เป็นเพียงวิธีง่ายๆในการติดฉลากส่วนประกอบของกราฟเช่นจุดยอดขอบและพื้นที่ภายใต้ข้อ จำกัด บางประการ ในกราฟไม่มีจุดยอดสองจุดที่อยู่ติดกันขอบที่อยู่ติดกันหรือบริเวณที่อยู่ติดกันจะถูกระบายสีด้วยจำนวนสีขั้นต่ำ หมายเลขนี้เรียกว่าchromatic number และกราฟเรียกว่า a properly colored graph.
ในขณะที่การระบายสีกราฟข้อ จำกัด ที่กำหนดไว้บนกราฟ ได้แก่ สีลำดับของการระบายสีวิธีการกำหนดสี ฯลฯ การระบายสีจะถูกกำหนดให้กับจุดยอดหรือพื้นที่เฉพาะ ดังนั้นจุดยอดหรือพื้นที่ที่มีสีเดียวกันจึงสร้างชุดอิสระ
เวอร์เท็กซ์ระบายสี
การระบายสีจุดยอดคือการกำหนดสีให้กับจุดยอดของกราฟ 'G' เพื่อให้จุดยอดสองจุดที่อยู่ติดกันไม่มีสีเหมือนกัน พูดง่ายๆคือไม่ควรมีจุดยอดสองจุดของขอบที่มีสีเดียวกัน
หมายเลขโครมาติก
จำนวนสีขั้นต่ำที่จำเป็นสำหรับการระบายสีจุดสุดยอดของกราฟ 'G' เรียกว่าเป็นจำนวนสีของ G ซึ่งแสดงด้วย X (G)
χ (G) = 1 เฉพาะในกรณีที่ 'G' เป็นกราฟว่าง ถ้า 'G' ไม่ใช่กราฟว่างดังนั้นχ (G) ≥ 2
Example
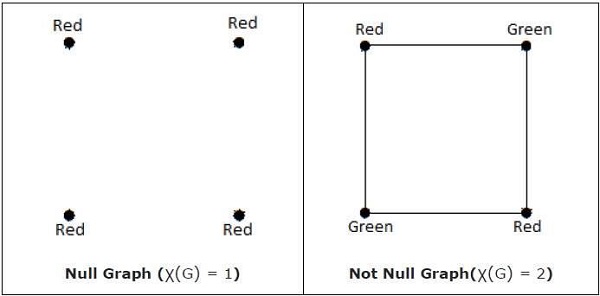
Note - กราฟ 'G' ถูกกล่าวว่าเป็น n-coverable หากมีจุดยอดสีที่ใช้สีมากที่สุด n สีเช่น X (G) ≤ n
ภูมิภาคระบายสี
การระบายสีตามภูมิภาคเป็นการกำหนดสีให้กับพื้นที่ของกราฟระนาบเพื่อให้ไม่มีพื้นที่ติดกันสองแห่งที่มีสีเหมือนกัน กล่าวกันว่าภูมิภาคสองแห่งอยู่ติดกันหากมีขอบร่วมกัน
Example
ดูกราฟต่อไปนี้ ภูมิภาค 'aeb' และ 'befc' อยู่ติดกันเนื่องจากมี 'be' ร่วมกันระหว่างภูมิภาคทั้งสอง
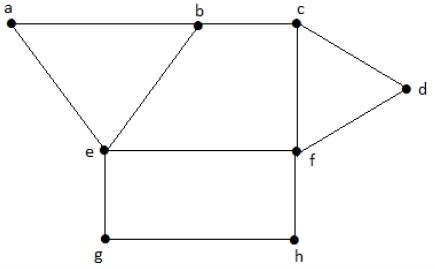
ในทำนองเดียวกันภูมิภาคอื่น ๆ จะมีสีตามความเหมาะสม กราฟนี้มีสีดังนี้ -
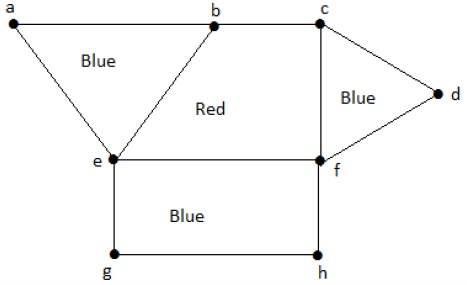
Example
จำนวนสีของ Kn คือ
- n
- n–1
- [n/2]
- [n/2]
ลองพิจารณาตัวอย่างนี้กับภาคที่ 4

ในกราฟที่สมบูรณ์จุดยอดแต่ละจุดอยู่ติดกับจุดยอดที่เหลือ (n - 1) ดังนั้นจุดยอดแต่ละจุดจึงต้องใช้สีใหม่ ดังนั้นจำนวนสีของ K n = n
การประยุกต์ใช้การระบายสีกราฟ
การระบายสีกราฟเป็นแนวคิดที่สำคัญที่สุดอย่างหนึ่งในทฤษฎีกราฟ ใช้ในการประยุกต์ใช้วิทยาการคอมพิวเตอร์แบบเรียลไทม์เช่น -
- Clustering
- การขุดข้อมูล
- การจับภาพ
- การแบ่งส่วนภาพ
- Networking
- การจัดสรรทรัพยากร
- การจัดกำหนดการกระบวนการ