ทฤษฎีกราฟ - การครอบคลุม
กราฟที่ครอบคลุมคือกราฟย่อยที่มีจุดยอดทั้งหมดหรือขอบทั้งหมดที่ตรงกับกราฟอื่น ๆ ย่อหน้าย่อยที่มีจุดยอดทั้งหมดเรียกว่า aline/edge covering. กราฟย่อยที่มีขอบทั้งหมดเรียกว่าไฟล์vertex covering.
การครอบคลุมเส้น
ให้ G = (V, E) เป็นกราฟ เซตย่อย C (E) เรียกว่าเส้นที่ครอบคลุม G ถ้าทุกจุดยอดของ G เกิดขึ้นโดยมีอย่างน้อยหนึ่งขอบใน C กล่าวคือ
องศา (V) ≥ 1 ∀ V ∈ G
เนื่องจากจุดยอดแต่ละจุดเชื่อมต่อกับจุดยอดอื่นด้วยขอบ ดังนั้นจึงมีระดับขั้นต่ำ 1
Example
ดูกราฟต่อไปนี้ -
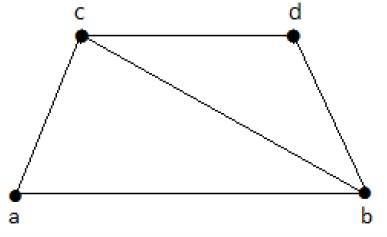
ย่อหน้าที่มีเส้นครอบคลุมมีดังนี้ -
ค1 = {{a, b}, {c, d}}
ค2 = {{a, d}, {b, c}}
ค3 = {{a, b}, {b, c}, {b, d}}
ค4 = {{a, b}, {b, c}, {c, d}}
ไม่มีการปิดทับเส้นของ 'G' ก็ต่อเมื่อ 'G' มีจุดยอดที่แยกได้ เส้นคลุมของกราฟที่มีจุดยอด 'n' มีขอบอย่างน้อย [n / 2]
การครอบคลุมบรรทัดน้อยที่สุด
เส้นที่ครอบคลุม C ของกราฟ G มีค่าน้อยที่สุด if no edge can be deleted from C.
Example
ในกราฟด้านบนกราฟย่อยที่มีเส้นครอบคลุมมีดังนี้ -
ค1 = {{a, b}, {c, d}}
ค2 = {{a, d}, {b, c}}
ค3 = {{a, b}, {b, c}, {b, d}}
ค4 = {{a, b}, {b, c}, {c, d}}
ในที่นี้ C 1 , C 2 , C 3เป็นการปิดทับเส้นขั้นต่ำในขณะที่ C 4ไม่ใช่เพราะเราสามารถลบ {b, c} ได้
การครอบคลุมบรรทัดขั้นต่ำ
เป็นที่รู้จักกันในชื่อ Smallest Minimal Line Covering. เส้นขั้นต่ำที่มีจำนวนขอบต่ำสุดเรียกว่าเส้นขั้นต่ำที่ครอบคลุม 'G' จำนวนขอบในเส้นขั้นต่ำที่ครอบคลุมใน 'G' เรียกว่าline covering numberของ 'G' (α 1 )
Example
ในตัวอย่างข้างต้น C 1และ C 2คือเส้นขั้นต่ำที่ครอบคลุมของ G และα 1 = 2
ทุกบรรทัดที่ครอบคลุมมีการปิดบรรทัดน้อยที่สุด
การครอบคลุมทุกบรรทัดไม่มีการปิดบรรทัดขั้นต่ำ (C 3ไม่มีการครอบคลุมบรรทัดขั้นต่ำ
ไม่มีการครอบคลุมบรรทัดขั้นต่ำที่ประกอบด้วยวัฏจักร
หากเส้นที่ครอบคลุม "C" ไม่มีเส้นทางที่มีความยาวตั้งแต่ 3 ขึ้นไป "C" จะเป็นเส้นเล็ก ๆ ที่ครอบคลุมเนื่องจากส่วนประกอบทั้งหมดของ "C" เป็นกราฟดาวและจากกราฟดาวจะไม่สามารถลบขอบได้
เวอร์เท็กซ์ครอบคลุม
ให้ 'G' = (V, E) เป็นกราฟ เซตย่อย K ของ V เรียกว่าจุดยอดที่ครอบคลุม 'G' ถ้าขอบทุกด้านของ 'G' เกิดขึ้นกับหรือปิดทับด้วยจุดยอดใน 'K'
Example
ดูกราฟต่อไปนี้ -
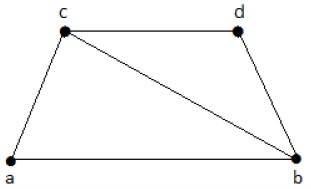
กราฟย่อยที่ได้มาจากกราฟด้านบนมีดังนี้ -
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}
ที่นี่ K 1 K 2และ K 3มีจุดยอดครอบคลุมในขณะที่ K 4ไม่มีจุดยอดครอบคลุมเนื่องจากไม่ครอบคลุมขอบ {bc}
ครอบคลุมจุดยอดน้อยที่สุด
จุดยอด 'K' ของกราฟ 'G' ถูกกล่าวว่าเป็นจุดยอดขั้นต่ำที่ครอบคลุมหากไม่สามารถลบจุดยอดออกจาก 'K' ได้
Example
ในกราฟด้านบนกราฟย่อยที่มีจุดยอดครอบคลุมมีดังนี้ -
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
ที่นี่ K 1และ K 2เป็นการปกปิดจุดยอดน้อยที่สุดในขณะที่ใน K 3จุดยอด 'd' สามารถลบได้
การครอบคลุมจุดยอดขั้นต่ำ
เป็นที่รู้จักกันว่าเป็นจุดยอดน้อยที่สุดที่ครอบคลุม จุดยอดขั้นต่ำที่ครอบคลุมกราฟ 'G' ที่มีจำนวนจุดยอดต่ำสุดเรียกว่าจุดยอดต่ำสุดที่ครอบคลุม
จำนวนจุดยอดในจุดยอดต่ำสุดที่ครอบคลุม 'G' เรียกว่าจุดยอดครอบคลุมจำนวน G (α 2 )
Example
ในกราฟต่อไปนี้กราฟย่อยที่มีจุดยอดครอบคลุมมีดังนี้ -
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}

ในที่นี้ K 1คือจุดยอดขั้นต่ำของ G เนื่องจากมีจุดยอดเพียงสองจุด α 2 = 2