ทฤษฎีกราฟ - การจับคู่
กราฟที่ตรงกันคือกราฟย่อยของกราฟที่ไม่มีขอบติดกัน เพียงแค่ไม่ควรมีจุดยอดทั่วไประหว่างสองขอบใด ๆ
การจับคู่
ให้ 'G' = (V, E) เป็นกราฟ ย่อหน้าย่อยเรียกว่า M (G) ที่ตรงกันif each vertex of G is incident with at most one edge in Mกล่าวคือ
องศา (V) ≤ 1 ∀ V ∈ G
ซึ่งหมายความว่าในกราฟที่ตรงกัน M (G) จุดยอดควรมีระดับ 1 หรือ 0 โดยที่ขอบควรจะตกกระทบจากกราฟ G
Notation - ม (G)
Example
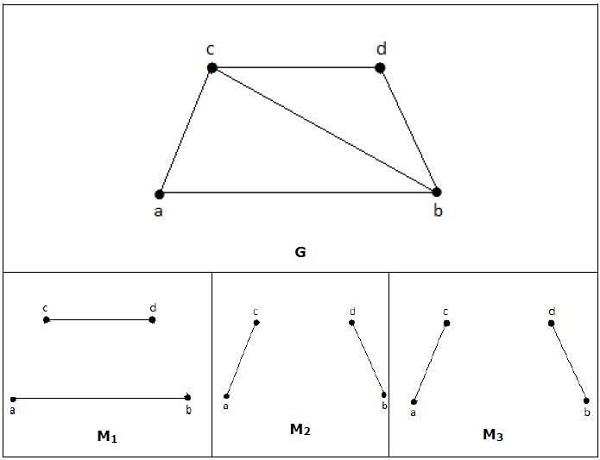

ในการจับคู่
ถ้า deg (V) = 1 ดังนั้น (V) จะบอกว่าตรงกัน
ถ้า deg (V) = 0 แสดงว่า (V) ไม่ตรงกัน
ในการจับคู่ไม่มีขอบสองด้านติดกัน เป็นเพราะถ้าสองขอบใด ๆ อยู่ติดกันดังนั้นระดับของจุดยอดที่เชื่อมขอบทั้งสองนั้นจะมีระดับเป็น 2 ซึ่งละเมิดกฎการจับคู่
การจับคู่สูงสุด
M ที่ตรงกันของกราฟ 'G' ถูกกล่าวว่ามีค่าสูงสุด if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 จากกราฟด้านบนเป็นการจับคู่สูงสุดของ G
การจับคู่สูงสุด
เรียกอีกอย่างว่าการจับคู่สูงสุดที่ใหญ่ที่สุด การจับคู่สูงสุดถูกกำหนดให้เป็นการจับคู่สูงสุดกับจำนวนขอบสูงสุด
จำนวนขอบในการจับคู่สูงสุดของ 'G' เรียกว่ามัน matching number.
Example
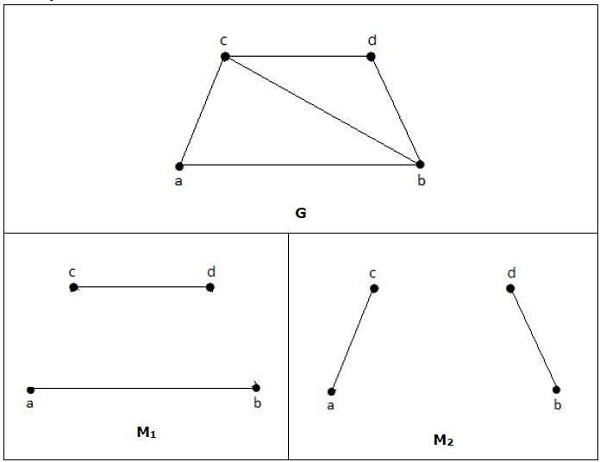
สำหรับกราฟที่ระบุในตัวอย่างข้างต้น M1 และ M2 เป็นการจับคู่สูงสุดของ 'G' และจำนวนที่ตรงกันคือ 2 ดังนั้นเมื่อใช้กราฟ G เราจึงสามารถสร้างกราฟย่อยที่มีขอบสูงสุดเพียง 2 ขอบเท่านั้น ดังนั้นเราจึงมีหมายเลขที่ตรงกันเป็นสอง
การจับคู่ที่สมบูรณ์แบบ
การจับคู่ (M) ของกราฟ (G) ถูกกล่าวว่าเป็นการจับคู่ที่สมบูรณ์แบบหากทุกจุดยอดของกราฟ g (G) เกิดขึ้นกับขอบด้านหนึ่งของการจับคู่ (M) นั่นคือ
องศา (V) = 1 ∀ V
ระดับของจุดยอดแต่ละจุดในกราฟย่อยควรมีระดับ 1
Example
ในกราฟต่อไปนี้ M1 และ M2 เป็นตัวอย่างของการจับคู่ G ที่สมบูรณ์แบบ
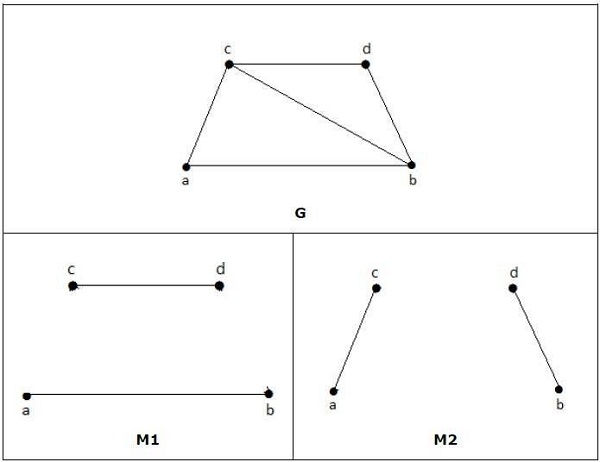
Note - การจับคู่กราฟที่สมบูรณ์แบบทุกครั้งเป็นการจับคู่กราฟสูงสุดเนื่องจากไม่มีโอกาสที่จะเพิ่มอีกหนึ่งขอบในกราฟการจับคู่ที่สมบูรณ์แบบ
การจับคู่กราฟสูงสุดไม่จำเป็นต้องสมบูรณ์แบบ หากกราฟ 'G' มีค่าที่ตรงกันจำนวนจุดยอด | V (G) | เป็นคู่ หากเป็นเลขคี่จุดยอดสุดท้ายจะจับคู่กับจุดยอดอื่นและสุดท้ายก็ยังคงมีจุดยอดเดียวซึ่งไม่สามารถจับคู่กับจุดยอดอื่นใดที่มีองศาเป็นศูนย์ มันละเมิดหลักการจับคู่ที่สมบูรณ์แบบอย่างชัดเจน
Example
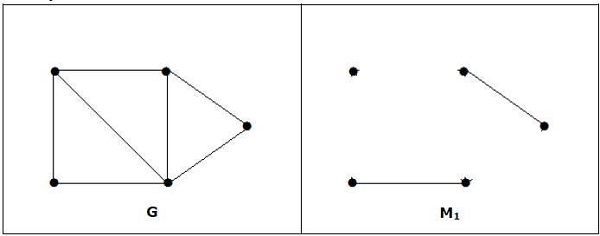
Note- การสนทนาของข้อความข้างต้นไม่จำเป็นต้องเป็นความจริง ถ้า G มีจำนวนจุดยอดเท่ากัน M1 ก็ไม่จำเป็นต้องสมบูรณ์แบบ
Example
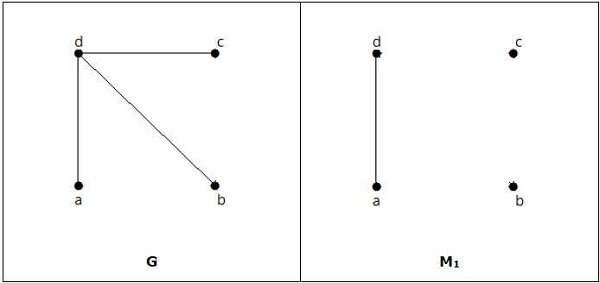
มันตรงกัน แต่ไม่ใช่การจับคู่ที่สมบูรณ์แบบแม้ว่าจะมีจำนวนจุดยอด