ทฤษฎีกราฟ - คู่มือฉบับย่อ

ประสิทธิภาพของคณิตศาสตร์และวิทยาการคอมพิวเตอร์, ทฤษฎีกราฟคือการศึกษาของกราฟที่กังวลกับความสัมพันธ์ระหว่างขอบและจุด เป็นวิชายอดนิยมที่มีการประยุกต์ใช้ในวิทยาศาสตร์คอมพิวเตอร์เทคโนโลยีสารสนเทศชีววิทยาศาสตร์คณิตศาสตร์และภาษาศาสตร์ โดยไม่ต้องกังวลใจเพิ่มเติมให้เราเริ่มต้นด้วยการกำหนดกราฟ

กราฟคืออะไร?

กราฟคือการแสดงภาพชุดของวัตถุที่คู่ของวัตถุบางคู่เชื่อมต่อกันด้วยลิงก์ วัตถุที่เชื่อมต่อกันจะแสดงด้วยจุดที่เรียกว่าverticesและลิงก์ที่เชื่อมต่อจุดยอดนั้นเรียกว่า edges.

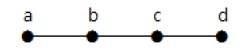
ปกติกราฟคือคู่ของเซต (V, E), ที่ไหน Vคือเซตของจุดยอดและ E คือเซตของขอบที่เชื่อมคู่ของจุดยอด ดูกราฟต่อไปนี้ -

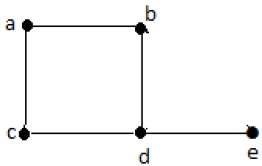
ในกราฟด้านบน

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

การประยุกต์ใช้ทฤษฎีกราฟ

ทฤษฎีกราฟมีการประยุกต์ใช้ในวิศวกรรมหลากหลายสาขา -

Electrical Engineering- แนวคิดของทฤษฎีกราฟถูกใช้อย่างกว้างขวางในการออกแบบการเชื่อมต่อวงจร ประเภทหรือองค์กรของการเชื่อมต่อถูกตั้งชื่อเป็นโทโพโลยี ตัวอย่างบางส่วนของโทโพโลยี ได้แก่ แบบดาวสะพานอนุกรมและโทโพโลยีแบบขนาน

Computer Science- ทฤษฎีกราฟใช้สำหรับการศึกษาอัลกอริทึม ตัวอย่างเช่น,

อัลกอริทึมของ Kruskal
อัลกอริทึมของ Prim
อัลกอริทึมของ Dijkstra

Computer Network - ความสัมพันธ์ระหว่างคอมพิวเตอร์ที่เชื่อมต่อกันในเครือข่ายเป็นไปตามหลักการของทฤษฎีกราฟ

Science - โครงสร้างโมเลกุลและโครงสร้างทางเคมีของสารโครงสร้างดีเอ็นเอของสิ่งมีชีวิต ฯลฯ แสดงด้วยกราฟ

Linguistics - โครงสร้างการแยกวิเคราะห์ของภาษาและไวยากรณ์ของภาษาใช้กราฟ

General- เส้นทางระหว่างเมืองสามารถแสดงโดยใช้กราฟ การแสดงข้อมูลที่เรียงลำดับตามลำดับชั้นเช่นแผนผังครอบครัวสามารถใช้เป็นกราฟชนิดพิเศษที่เรียกว่าทรี

กราฟคือแผนภาพของจุดและเส้นที่เชื่อมต่อกับจุด มีอย่างน้อยหนึ่งบรรทัดที่เชื่อมต่อกับชุดของจุดยอดสองจุดโดยไม่มีจุดยอดเชื่อมต่อตัวเอง แนวคิดของกราฟในทฤษฎีกราฟขึ้นอยู่กับคำพื้นฐานบางคำเช่นจุดเส้นจุดยอดขอบองศาของจุดยอดคุณสมบัติของกราฟเป็นต้นในบทนี้เราจะกล่าวถึงพื้นฐานของทฤษฎีกราฟเหล่านี้

จุด

A pointคือตำแหน่งเฉพาะในปริภูมิหนึ่งมิติสองมิติหรือสามมิติ เพื่อความเข้าใจที่ดีขึ้นจุดสามารถแสดงด้วยตัวอักษร สามารถแทนด้วยจุด

ตัวอย่าง

จุดนี้คือจุดที่มีชื่อว่า 'a'

ไลน์

ก Lineเป็นการเชื่อมต่อระหว่างสองจุด สามารถแสดงด้วยเส้นทึบ

Example

ที่นี่ 'a' และ 'b' คือจุด จุดเชื่อมระหว่างสองจุดนี้เรียกว่าเส้น

จุดยอด

จุดยอดคือจุดที่เส้นหลายเส้นมาบรรจบกัน เรียกอีกอย่างว่าnode. เช่นเดียวกับจุดจุดยอดยังแสดงด้วยตัวอักษร

Example

ที่นี่จุดยอดถูกตั้งชื่อด้วยตัวอักษร 'a'

ขอบ

edge คือคำศัพท์ทางคณิตศาสตร์สำหรับเส้นที่เชื่อมต่อจุดยอดสองจุด ขอบจำนวนมากสามารถเกิดขึ้นจากจุดยอดเดียว หากไม่มีจุดยอดจะไม่สามารถสร้างขอบได้ ต้องมีจุดยอดเริ่มต้นและจุดยอดสิ้นสุดสำหรับขอบ

Example

ที่นี่ 'a' และ 'b' คือจุดยอดสองจุดและจุดเชื่อมระหว่างพวกเขาเรียกว่าขอบ

กราฟ

กราฟ 'G' ถูกกำหนดให้เป็น G = (V, E) โดยที่ V คือชุดของจุดยอดทั้งหมดและ E คือชุดของขอบทั้งหมดในกราฟ

Example 1

ในตัวอย่างข้างต้น ab, ac, cd และ bd คือขอบของกราฟ ในทำนองเดียวกัน a, b, c และ d คือจุดยอดของกราฟ

Example 2

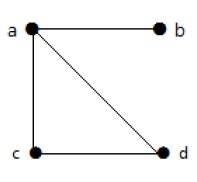
ในกราฟนี้มีจุดยอด a, b, c และ d สี่จุดและสี่ขอบ ab, ac, ad และ cd

วน

ในกราฟถ้าขอบวาดจากจุดยอดถึงตัวมันเองจะเรียกว่าการวนซ้ำ

Example 1

ในกราฟด้านบน V คือจุดยอดที่มีขอบ (V, V) สร้างวง

Example 2

ในกราฟนี้มีสองลูปซึ่งเกิดขึ้นที่จุดยอด a และจุดยอด b

ระดับของจุดยอด

มันคือจำนวนจุดยอดที่อยู่ติดกับจุดยอด V

Notation - องศา (V)

ในกราฟธรรมดาที่มีจุดยอดจำนวน n ระดับของจุดยอดใด ๆ คือ -

องศา (v) ≤ n - 1 ∀ v ∈ G

จุดยอดสามารถสร้างขอบกับจุดยอดอื่น ๆ ทั้งหมดยกเว้นด้วยตัวมันเอง ดังนั้นระดับของจุดยอดจะขึ้นอยู่กับnumber of vertices in the graph minus 1. 1 นี้มีไว้สำหรับจุดยอดในตัวเองเนื่องจากไม่สามารถสร้างลูปด้วยตัวเองได้ หากมีการวนซ้ำที่จุดยอดใด ๆ แสดงว่าไม่ใช่กราฟแบบง่าย

ระดับของจุดยอดสามารถพิจารณาได้ภายใต้กราฟสองกรณี -

กราฟที่ไม่ได้บอกทิศทาง
กราฟกำกับ

ระดับของจุดยอดในกราฟที่ไม่ได้บอกทิศทาง

กราฟที่ไม่มีทิศทางไม่มีขอบกำกับ ลองพิจารณาตัวอย่างต่อไปนี้

Example 1

ดูกราฟต่อไปนี้ -

ในกราฟ Undirected ด้านบน

deg (a) = 2 เนื่องจากมีขอบ 2 ด้านมาบรรจบกันที่จุดยอด 'a'
deg (b) = 3 เนื่องจากมีขอบ 3 ด้านมาบรรจบกันที่จุดยอด 'b'
deg (c) = 1 เนื่องจากมีขอบ 1 เกิดขึ้นที่จุดยอด 'c'
ดังนั้น 'c' คือ a pendent vertex.
deg (d) = 2 เนื่องจากมีขอบ 2 ด้านมาพบกันที่จุดยอด 'd'
deg (e) = 0 เนื่องจากมีขอบ 0 เกิดขึ้นที่จุดยอด 'e'
ดังนั้น 'e' จึงเป็นไฟล์ isolated vertex.

Example 2

ดูกราฟต่อไปนี้ -

ในกราฟด้านบน

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 และ deg (e) = 0

จุดยอด 'e' คือจุดยอดที่แยกได้ กราฟไม่มีจุดยอดจี้ใด ๆ

ระดับของจุดยอดในกราฟกำกับ

ในกราฟกำกับจุดยอดแต่ละจุดมีเครื่องหมาย indegree และ outdegree.

ดัชนีของกราฟ

Indegree ของจุดยอด V คือจำนวนขอบที่เข้ามาในจุดยอด V
Notation - deg− (V)

ค่ามาตรฐานของกราฟ

Outdegree ของจุดยอด V คือจำนวนขอบที่ยื่นออกไปจากจุดยอด V
Notation - องศา + (V)

ลองพิจารณาตัวอย่างต่อไปนี้

Example 1

ดูกราฟกำกับต่อไปนี้ Vertex 'a' มีสองขอบ 'ad' และ 'ab' ซึ่งจะออกไปด้านนอก ดังนั้นค่าสูงสุดของมันคือ 2 ในทำนองเดียวกันมีขอบ 'ga' มาทางจุดยอด 'a' ดังนั้นดัชนีของ 'a' คือ 1

ดัชนีและจุดสูงสุดของจุดยอดอื่น ๆ แสดงไว้ในตารางต่อไปนี้ -

จุดยอด	Indegree	ปริญญาตรี
ก	1	2
ข	2	0
ค	2	1
ง	1	1
จ	1	1
ฉ	1	1
ก	0	2

Example 2

ดูกราฟกำกับต่อไปนี้ จุดยอด 'a' มีขอบ 'ae' ออกไปจากจุดยอด 'a' ดังนั้นค่า outdegree คือ 1 ในทำนองเดียวกันกราฟจะมีขอบ 'ba' มาทางจุดยอด 'a' ดังนั้นดัชนีของ 'a' คือ 1

ดัชนีและจุดสูงสุดของจุดยอดอื่น ๆ แสดงไว้ในตารางต่อไปนี้ -

จุดยอด	Indegree	ปริญญาตรี
ก	1	1
ข	0	2
ค	2	0
ง	1	1
จ	1	1

Pendent Vertex

ด้วยการใช้องศาของจุดยอดเรามีจุดยอดพิเศษสองประเภท จุดยอดที่มีดีกรีหนึ่งเรียกว่าจุดยอดแบบจี้

Example

ในตัวอย่างนี้จุดยอด 'a' และจุดยอด 'b' มีขอบที่เชื่อมต่อกัน 'ab' ดังนั้นในส่วนที่เกี่ยวกับจุดยอด 'a' จึงมีขอบเพียงด้านเดียวเท่านั้นที่นำไปสู่จุดยอด 'b' และในทำนองเดียวกันเมื่อเทียบกับจุดยอด 'b' มีขอบเพียงด้านเดียวที่นำไปสู่จุดยอด 'a' ในที่สุดจุดยอด 'a' และจุดยอด 'b' มีระดับเป็นหนึ่งซึ่งเรียกอีกอย่างว่าจุดยอดจี้

จุดยอดที่แยกได้

จุดยอดที่มีองศาศูนย์เรียกว่าจุดยอดแยก

Example

ที่นี่จุดยอด 'a' และจุดยอด 'b' ไม่มีการเชื่อมต่อระหว่างกันและยังจุดยอดอื่น ๆ ดังนั้นระดับของจุดยอดทั้งสอง 'a' และ 'b' จึงเป็นศูนย์ สิ่งเหล่านี้เรียกอีกอย่างว่าจุดยอดแยก

Adjacency

นี่คือบรรทัดฐานของความใกล้ชิด -

ในกราฟจะมีจุดยอด 2 จุด adjacentถ้ามีขอบระหว่างจุดยอดทั้งสอง ที่นี่ความใกล้ชิดของจุดยอดจะถูกคงไว้โดยขอบด้านเดียวที่เชื่อมต่อจุดยอดทั้งสองนั้น
ในกราฟกล่าวว่าสองขอบอยู่ติดกันหากมีจุดยอดร่วมระหว่างขอบทั้งสอง ที่นี่ความใกล้ชิดของขอบถูกรักษาโดยจุดยอดเดียวที่เชื่อมต่อสองขอบ

Example 1

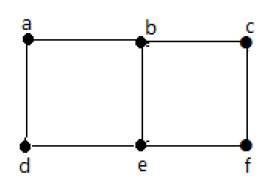
ในกราฟด้านบน -

'a' และ 'b' เป็นจุดยอดที่อยู่ติดกันเนื่องจากมีขอบ 'ab' ร่วมกันระหว่างพวกเขา
'a' และ 'd' เป็นจุดยอดที่อยู่ติดกันเนื่องจากมีขอบ 'โฆษณา' ร่วมกัน
ab 'และ' be 'เป็นขอบที่อยู่ติดกันเนื่องจากมีจุดยอดทั่วไป' b 'อยู่ระหว่างพวกเขา
be 'และ' de 'คือขอบที่อยู่ติดกันเนื่องจากมีจุดยอด' e 'ร่วมกันระหว่างพวกเขา

Example 2

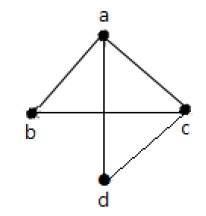
ในกราฟด้านบน -

'a' และ 'd' เป็นจุดยอดที่อยู่ติดกันเนื่องจากมีขอบ 'โฆษณา' ร่วมกัน
'c' และ 'b' เป็นจุดยอดที่อยู่ติดกันเนื่องจากมีขอบ 'cb' ร่วมด้วย
'ad' และ 'cd' คือขอบที่อยู่ติดกันเนื่องจากมีจุดยอด 'd' ร่วมกัน
'ac' และ 'cd' เป็นขอบที่อยู่ติดกันเนื่องจากมีจุดยอดทั่วไป 'c' อยู่ระหว่างพวกเขา

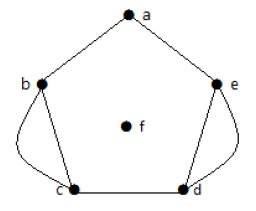
ขอบขนาน

ในกราฟถ้าจุดยอดหนึ่งคู่เชื่อมต่อกันด้วยขอบมากกว่าหนึ่งขอบจะเรียกว่าขอบขนาน

ในกราฟด้านบน 'a' และ 'b' คือจุดยอดสองจุดที่เชื่อมต่อกันด้วยขอบสองด้าน 'ab' และ 'ab' ระหว่างพวกเขา จึงเรียกว่าเป็นขอบขนาน

หลายกราฟ

กราฟที่มีขอบขนานเรียกว่า Multigraph

Example 1

ในกราฟด้านบนมีห้าขอบ 'ab', 'ac', 'cd', 'cd' และ 'bd' เนื่องจาก 'c' และ 'd' มีสองขอบขนานระหว่างกันจึงเป็น Multigraph

Example 2

ในกราฟด้านบนจุดยอด 'b' และ 'c' มีสองขอบ จุดยอด 'e' และ 'd' ยังมีสองขอบระหว่างพวกเขา ดังนั้นจึงเป็น Multigraph

ลำดับองศาของกราฟ

ถ้าองศาของจุดยอดทั้งหมดในกราฟเรียงลำดับจากมากไปหาน้อยหรือจากน้อยไปหามากลำดับที่ได้รับจะเรียกว่าลำดับองศาของกราฟ

Example 1

จุดยอด	ก	ข	ค	ง	จ
เชื่อมต่อกับ	ข, ค	ก, ง	ก, ง	ค, ข, จ	ง
ระดับ	2	2	2	3	1

ในกราฟด้านบนสำหรับจุดยอด {d, a, b, c, e} ลำดับองศาคือ {3, 2, 2, 2, 1}

Example 2

จุดยอด	ก	ข	ค	ง	จ	ฉ
เชื่อมต่อกับ	ข, จ	ก, ค	ข, ง	ค, จ	ก, ง	-
ระดับ	2	2	2	2	2	0

ในกราฟด้านบนสำหรับจุดยอด {a, b, c, d, e, f} ลำดับองศาคือ {2, 2, 2, 2, 2, 0}

กราฟมาพร้อมกับคุณสมบัติต่างๆที่ใช้สำหรับการกำหนดลักษณะของกราฟขึ้นอยู่กับโครงสร้าง คุณสมบัติเหล่านี้กำหนดไว้ในเงื่อนไขเฉพาะที่เกี่ยวข้องกับโดเมนของทฤษฎีกราฟ ในบทนี้เราจะพูดถึงคุณสมบัติพื้นฐานบางประการที่มีอยู่ทั่วไปในกราฟทั้งหมด

ระยะห่างระหว่างจุดยอดสองจุด

เป็นจำนวนขอบในเส้นทางที่สั้นที่สุดระหว่าง Vertex U และ Vertex V หากมีหลายเส้นทางเชื่อมต่อจุดยอดสองจุดเส้นทางที่สั้นที่สุดจะถือเป็นระยะห่างระหว่างจุดยอดทั้งสอง

สัญกรณ์ - d (U, V)

สามารถมีเส้นทางจำนวนเท่าใดก็ได้จากจุดยอดหนึ่งไปยังอีกจุดหนึ่ง คุณต้องเลือกข้อที่สั้นที่สุดเท่านั้น

Example

ดูกราฟต่อไปนี้ -

ในที่นี้ระยะห่างจากจุดยอด 'd' ถึงจุดยอด 'e' หรือเพียงแค่ 'เดอ' คือ 1 เนื่องจากมีขอบหนึ่งระหว่างพวกเขา มีหลายเส้นทางจากจุดยอด 'd' ถึงจุดยอด 'e' -

ดา ab เป็น
df, fg, ge
de (ถือเป็นระยะห่างระหว่างจุดยอด)
df, fc, ca, ab, เป็น
ดา, ac, cf, fg, ge

ความเยื้องศูนย์ของจุดยอด

ระยะห่างสูงสุดระหว่างจุดยอดถึงจุดยอดอื่น ๆ ทั้งหมดถือเป็นความเยื้องศูนย์กลางของจุดยอด

สัญกรณ์ - e (V)

ระยะทางจากจุดยอดหนึ่งไปยังจุดยอดอื่น ๆ ทั้งหมดในกราฟจะถูกนำมาและในบรรดาระยะทางเหล่านั้นความเยื้องศูนย์กลางคือระยะทางสูงสุด

Example

ในกราฟด้านบนความเยื้องศูนย์ของ 'a' คือ 3

ระยะทางจาก 'a' ถึง 'b' คือ 1 ('ab'),

จาก 'a' ถึง 'c' คือ 1 ('ac'),

จาก 'a' ถึง 'd' คือ 1 ('ad'),

จาก 'a' ถึง 'e' คือ 2 ('ab' - 'be') หรือ ('ad' - 'de'),

จาก 'a' ถึง 'f' คือ 2 ('ac' - 'cf') หรือ ('ad' - 'df'),

จาก 'a' ถึง 'g' คือ 3 ('ac' - 'cf' - 'fg') หรือ ('ad' - 'df' - 'fg')

ดังนั้นความเยื้องศูนย์คือ 3 ซึ่งเป็นค่าสูงสุดจากจุดยอด 'a' จากระยะห่างระหว่าง 'ag' ซึ่งเป็นค่าสูงสุด

กล่าวอีกนัยหนึ่ง

e (b) = 3

e (c) = 3

e (d) = 2

e (จ) = 3

e (f) = 3

e (g) = 3

รัศมีของกราฟที่เชื่อมต่อ

ความเบี้ยวต่ำสุดจากจุดยอดทั้งหมดถือเป็นรัศมีของกราฟ G ค่าต่ำสุดของระยะทางสูงสุดระหว่างจุดยอดถึงจุดยอดอื่น ๆ ทั้งหมดถือเป็นรัศมีของกราฟ G

สัญกรณ์ - r (G)

จากความเยื้องศูนย์ทั้งหมดของจุดยอดในกราฟรัศมีของกราฟที่เชื่อมต่อคือค่าต่ำสุดของความเยื้องศูนย์ทั้งหมด

Example

ในกราฟด้านบน r (G) = 2 ซึ่งเป็นค่าความเยื้องศูนย์กลางขั้นต่ำสำหรับ 'd'

เส้นผ่านศูนย์กลางของกราฟ

ความเยื้องศูนย์สูงสุดจากจุดยอดทั้งหมดถือเป็นเส้นผ่านศูนย์กลางของกราฟ G ค่าสูงสุดของระยะทางทั้งหมดระหว่างจุดยอดถึงจุดยอดอื่น ๆ ทั้งหมดถือเป็นเส้นผ่านศูนย์กลางของกราฟ G

Notation − d(G) - จากความเยื้องศูนย์ทั้งหมดของจุดยอดในกราฟเส้นผ่านศูนย์กลางของกราฟที่เชื่อมต่อคือค่าสูงสุดของความเยื้องศูนย์กลางเหล่านั้นทั้งหมด

Example

ในกราฟด้านบน d (G) = 3; ซึ่งเป็นค่าความเยื้องศูนย์สูงสุด

เซ็นทรัลพอยท์

ถ้าความเบี้ยวของกราฟเท่ากับรัศมีแสดงว่าเป็นจุดศูนย์กลางของกราฟ ถ้า

จ (V) = r (V),

จากนั้น "V" คือจุดศูนย์กลางของกราฟ "G"

Example

ในกราฟตัวอย่าง 'd' คือจุดศูนย์กลางของกราฟ

e (d) = r (d) = 2

ศูนย์

ชุดของจุดกลางทั้งหมดของ 'G' เรียกว่าศูนย์กลางของกราฟ

Example

ในกราฟตัวอย่าง {'d'} คือศูนย์กลางของกราฟ

เส้นรอบวง

number of edges in the longest cycle of ‘G’ เรียกว่าเส้นรอบวงของ 'G'

Example

ในกราฟตัวอย่างเส้นรอบวงคือ 6 ซึ่งเราได้มาจากวงจร acfgeba หรือ acfdeba ที่ยาวที่สุด

เส้นรอบวง

จำนวนขอบในรอบที่สั้นที่สุดของ 'G' เรียกว่าเส้นรอบวง

Notation: กรัม (G)

Example - ในกราฟตัวอย่างเส้นรอบวงของกราฟคือ 4 ซึ่งเราได้มาจากวงจร acfda ที่สั้นที่สุดหรือ dfged หรือ abeda

ผลรวมขององศาของจุดยอดทฤษฎีบท

ถ้า G = (V, E) เป็นกราฟที่ไม่มีทิศทางที่มีจุดยอด V = {V ₁ , V ₂ , … V _n } แล้ว

n Σ i = 1 องศา (V _i ) = 2 | E |

Corollary 1

ถ้า G = (V, E) เป็นกราฟกำกับด้วยจุดยอด V = {V ₁ , V ₂ , … V _n } แล้ว

n Σ i = 1 deg + (V _i ) = | E | = n Σผม = 1 deg− (V _i )

Corollary 2

ในกราฟที่ไม่กำหนดทิศทางจำนวนจุดยอดที่มีองศาคี่คือคู่

Corollary 3

ในกราฟที่ไม่ชี้นำหากระดับของจุดยอดแต่ละจุดคือ k ดังนั้น

k | V | = 2 | E |

Corollary 4

ในกราฟแบบไม่ชี้นำหากระดับของจุดยอดแต่ละจุดมีค่าอย่างน้อย k ดังนั้น

k | V | ≤ 2 | E |

| Corollary 5

ในกราฟที่ไม่ชี้นำหากระดับของจุดยอดแต่ละจุดมีค่ามากที่สุด k ดังนั้น

k | V | ≥ 2 | E |

กราฟมีหลายประเภทขึ้นอยู่กับจำนวนจุดยอดจำนวนขอบการเชื่อมต่อระหว่างกันและโครงสร้างโดยรวม เราจะพูดถึงกราฟที่สำคัญบางประเภทในบทนี้

กราฟ Null

A graph having no edges เรียกว่ากราฟ Null

ตัวอย่าง

ในกราฟด้านบนมีจุดยอดสามจุดชื่อ 'a', 'b' และ 'c' แต่ไม่มีขอบอยู่ ดังนั้นจึงเป็นกราฟ Null

กราฟเล็กน้อย

ก graph with only one vertex เรียกว่า Trivial Graph

ตัวอย่าง

ในกราฟที่แสดงด้านบนมีจุดยอด 'a' เพียงจุดเดียวที่ไม่มีขอบอื่น ๆ ดังนั้นมันจึงเป็นกราฟเล็กน้อย

กราฟที่ไม่ใช่ทิศทาง

กราฟที่ไม่ชี้นำมีขอบ แต่ขอบไม่ได้ชี้นำ

ตัวอย่าง

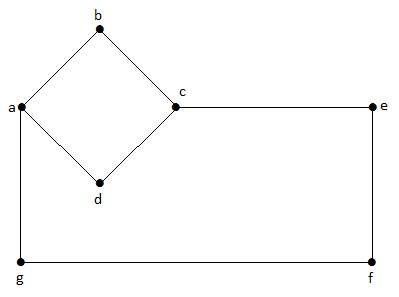
ในกราฟนี้ 'a', 'b', 'c', 'd', 'e', 'f', 'g' คือจุดยอดและ 'ab', 'bc', 'cd', 'da ',' ag ',' gf ',' ef 'คือขอบของกราฟ เนื่องจากเป็นกราฟแบบไม่กำหนดทิศทางขอบ "ab" และ "ba" จึงเหมือนกัน ในทำนองเดียวกันขอบอื่น ๆ ก็พิจารณาในลักษณะเดียวกัน

กราฟกำกับ

ในกราฟกำกับขอบแต่ละด้านมีทิศทาง

ตัวอย่าง

ในกราฟด้านบนเรามีจุดยอดเจ็ดจุด 'a', 'b', 'c', 'd', 'e', 'f' และ 'g' และแปดขอบ 'ab', 'cb', ' dc ',' ad ',' ec ',' fe ',' gf 'และ' ga ' เนื่องจากเป็นกราฟกำกับขอบแต่ละด้านจะมีเครื่องหมายลูกศรเพื่อแสดงทิศทาง โปรดทราบว่าในกราฟกำกับ "ab" จะแตกต่างจาก "ba"

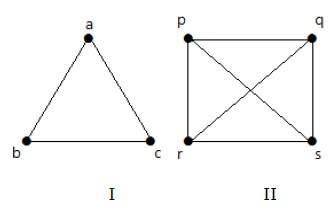
กราฟอย่างง่าย

กราฟ with no loops และไม่ parallel edges เรียกว่ากราฟธรรมดา

จำนวนขอบสูงสุดที่เป็นไปได้ในกราฟเดียวที่มีจุดยอด 'n' คือⁿ C ₂โดยที่ⁿ C ₂ = n (n - 1) / 2
จำนวนของกราฟที่เรียบง่ายเป็นไปได้ด้วย 'n' จุด = 2 _ⁿค₂ = 2 ^{n (n-1) /} 2

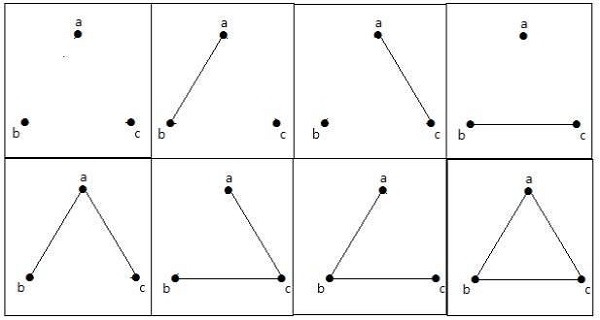
ตัวอย่าง

ในกราฟต่อไปนี้มีจุดยอด 3 จุดที่มี 3 ขอบซึ่งสูงสุดไม่รวมขอบขนานและลูป สามารถพิสูจน์ได้โดยใช้สูตรข้างต้น

จำนวนขอบสูงสุดที่มีจุดยอด n = 3 -

ⁿ C ₂ = n (n – 1) / 2

= 3 (3–1) / 2

= 6/2

= 3 ขอบ

จำนวนกราฟอย่างง่ายสูงสุดที่มีจุดยอด n = 3 -

2 _{ⁿ C ₂} = 2 ^{n (n-1) / 2}

= 2 ^{3 (3-1) / 2}

= 2 ³

กราฟทั้ง 8 ดังแสดงด้านล่าง -

กราฟที่เชื่อมต่อ

กราฟ G บอกว่าเชื่อมต่อกัน if there exists a path between every pair of vertices. ควรมีอย่างน้อยหนึ่งขอบสำหรับทุกจุดยอดในกราฟ เราจึงบอกได้ว่ามันเชื่อมต่อกับจุดยอดอื่น ๆ ที่อีกด้านของขอบ

ตัวอย่าง

ในกราฟต่อไปนี้จุดยอดแต่ละจุดมีขอบของตัวเองที่เชื่อมต่อกับขอบอื่น ๆ ดังนั้นจึงเป็นกราฟที่เชื่อมต่อกัน

กราฟที่ไม่ได้เชื่อมต่อ

กราฟ G ถูกตัดการเชื่อมต่อหากไม่มีจุดยอดที่เชื่อมต่ออย่างน้อยสองจุด

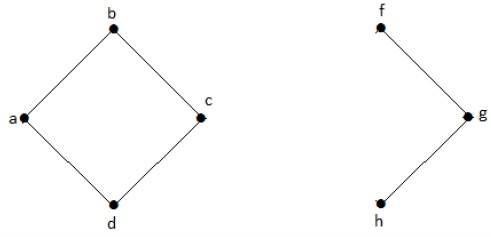
ตัวอย่าง 1

กราฟต่อไปนี้เป็นตัวอย่างของ Disconnected Graph ซึ่งมีองค์ประกอบสองส่วนโดยหนึ่งมีจุดยอด 'a', 'b', 'c', 'd' และอีกอันที่มี 'e', 'f', 'g', จุดยอด 'h'

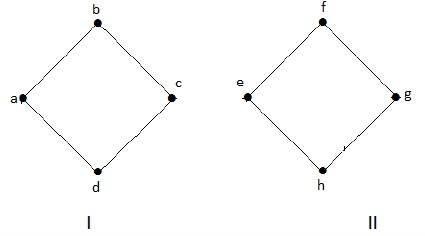
ส่วนประกอบทั้งสองเป็นอิสระและไม่เชื่อมต่อกัน ดังนั้นจึงเรียกว่ากราฟขาดการเชื่อมต่อ

ตัวอย่าง 2

ในตัวอย่างนี้มีส่วนประกอบอิสระสองส่วนคือ abfe และ cd ซึ่งไม่ได้เชื่อมต่อกัน ดังนั้นนี่คือกราฟที่ขาดการเชื่อมต่อ

กราฟปกติ

กราฟ G ถูกกล่าวว่าเป็นปกติ if all its vertices have the same degree. ในกราฟถ้าระดับของจุดยอดแต่ละจุดเป็น 'k' กราฟจะเรียกว่า 'กราฟ k-regular'

ตัวอย่าง

ในกราฟต่อไปนี้จุดยอดทั้งหมดมีองศาเดียวกัน ดังนั้นกราฟเหล่านี้จึงเรียกว่ากราฟปกติ

ในกราฟทั้งสองจุดยอดทั้งหมดมีองศา 2 เรียกว่ากราฟ 2-Regular

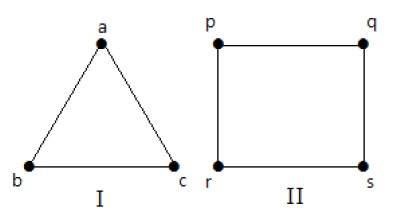
กราฟที่สมบูรณ์

กราฟอย่างง่ายที่มีจุดยอดร่วม 'n' เรียกว่ากราฟที่สมบูรณ์และเป็น denoted by ‘K_n’. ในกราฟa vertex should have edges with all other verticesจากนั้นเรียกว่ากราฟที่สมบูรณ์

กล่าวอีกนัยหนึ่งถ้าจุดยอดเชื่อมต่อกับจุดยอดอื่น ๆ ทั้งหมดในกราฟจะเรียกว่ากราฟที่สมบูรณ์

ตัวอย่าง

ในกราฟต่อไปนี้จุดยอดแต่ละจุดในกราฟจะเชื่อมต่อกับจุดยอดที่เหลือทั้งหมดในกราฟยกเว้นด้วยตัวมันเอง

ในกราฟ I

	ก	ข	ค
ก	ไม่ได้เชื่อมต่อ	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว
ข	เชื่อมต่อแล้ว	ไม่ได้เชื่อมต่อ	เชื่อมต่อแล้ว
ค	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว	ไม่ได้เชื่อมต่อ

ในกราฟ II

	น	q	ร	เอส
น	ไม่ได้เชื่อมต่อ	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว
q	เชื่อมต่อแล้ว	ไม่ได้เชื่อมต่อ	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว
ร	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว	ไม่ได้เชื่อมต่อ	เชื่อมต่อแล้ว
เอส	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว	เชื่อมต่อแล้ว	ไม่ได้เชื่อมต่อ

กราฟวงจร

กราฟอย่างง่ายที่มีจุดยอด 'n' (n> = 3) และขอบ 'n' เรียกว่ากราฟวัฏจักรหากขอบทั้งหมดเป็นวัฏจักรของความยาว 'n'

หากระดับของจุดยอดแต่ละจุดในกราฟเป็นสองจะเรียกว่ากราฟวัฏจักร

Notation- C _n

ตัวอย่าง

ดูกราฟต่อไปนี้ -

กราฟฉันมีจุดยอด 3 จุดที่มีขอบ 3 ด้านซึ่งก่อตัวเป็นวัฏจักร 'ab-bc-ca'
กราฟ II มีจุดยอด 4 จุดที่มีขอบ 4 จุดซึ่งก่อตัวเป็นวัฏจักร 'pq-qs-sr-rp'
กราฟ III มี 5 จุดยอดที่มี 5 ขอบซึ่งก่อตัวเป็นวัฏจักร 'ik-km-ml-lj-ji'

ดังนั้นกราฟที่กำหนดทั้งหมดจึงเป็นกราฟวัฏจักร

กราฟล้อ

กราฟวงล้อได้มาจากกราฟวัฏจักร C _n-1โดยการเพิ่มจุดยอดใหม่ จุดยอดใหม่นั้นเรียกว่า aHubซึ่งเชื่อมต่อไปยังทุกจุดของ C n

สัญกรณ์ - W _n

จำนวนขอบใน W _n = จำนวนขอบจากฮับไปยังจุดยอดอื่น ๆ ทั้งหมด +

จำนวนขอบจากโหนดอื่น ๆ ทั้งหมดในกราฟวัฏจักรที่ไม่มีฮับ

= (n – 1) + (n – 1)

= 2 (n – 1)

ตัวอย่าง

ดูกราฟต่อไปนี้ เป็นกราฟล้อทั้งหมด

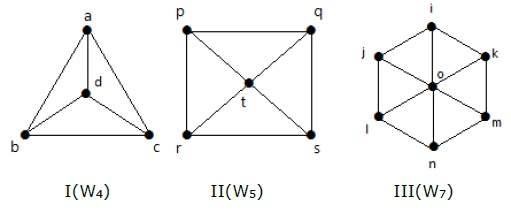
ในกราฟ I ได้มาจาก C ₃โดยการเพิ่มจุดยอดที่ตรงกลางซึ่งมีชื่อว่า 'd' มันเป็นเรื่องที่แสดงเป็น W 4

จำนวนขอบใน W4 = 2 (n-1) = 2 (3) = 6

ในกราฟ II ได้มาจาก C4 โดยการเพิ่มจุดยอดที่ตรงกลางซึ่งมีชื่อว่า 't' มันเป็นเรื่องที่แสดงเป็น W 5

จำนวนขอบใน W5 = 2 (n-1) = 2 (4) = 8

ในกราฟ III ได้มาจาก C ₆โดยการเพิ่มจุดยอดที่ตรงกลางชื่อ 'o' มันเป็นเรื่องที่แสดงเป็น W 7

จำนวนขอบใน W4 = 2 (n-1) = 2 (6) = 12

กราฟไซคลิก

กราฟ with at least one วงจรเรียกว่ากราฟวัฏจักร

ตัวอย่าง

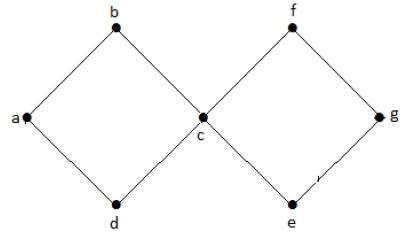
ในกราฟตัวอย่างด้านบนเรามีสองรอบ abcda และ cfgec ดังนั้นจึงเรียกว่ากราฟวัฏจักร

กราฟ Acyclic

กราฟ with no cycles เรียกว่ากราฟอะไซคลิก

ตัวอย่าง

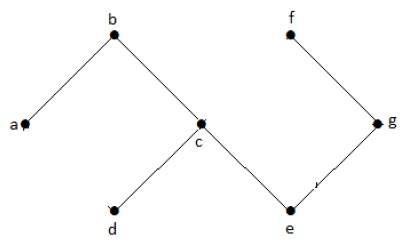
ในกราฟตัวอย่างข้างต้นเราไม่มีรอบใด ๆ ดังนั้นจึงเป็นกราฟที่ไม่ใช่วงจร

กราฟ Bipartite

กราฟอย่างง่าย G = (V, E) ที่มีจุดยอดพาร์ติชัน V = {V ₁ , V ₂ } เรียกว่ากราฟสองส่วนif every edge of E joins a vertex in V1 to a vertex in V₂.

โดยทั่วไปกราฟ Bipertite มีสองชุดของจุดให้เราพูด V1 และ V2 และถ้าขอบจะถูกวาดก็ควรเชื่อมต่อจุดสุดยอดใด ๆ ในชุด V ₁จุดสุดยอดใด ๆ ในชุด V 2

ตัวอย่าง

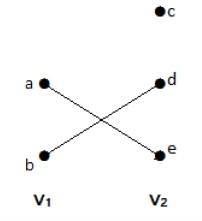
ในกราฟนี้คุณสามารถสังเกตเห็นสองชุดของจุด - V ₁และ V 2ที่นี่สองขอบชื่อว่า 'AE' และ 'BD' กำลังเชื่อมต่อจุดของสองชุดวี₁และวี2

ทำกราฟ Bipartite ให้สมบูรณ์

ฝ่ายกราฟ 'G' G = (V, E) กับพาร์ทิชัน V = {V ₁ , V ₂ } บอกว่าจะเป็นฝ่ายกราฟเสร็จสมบูรณ์หากจุดสุดยอดในทุก V ₁เชื่อมต่อกับจุดสุดยอดของ V ทุก2

โดยทั่วไปฝ่ายกราฟสมบูรณ์เชื่อมต่อแต่ละจุดสุดยอดจากชุด V ₁แต่ละจุดสุดยอดจากชุด V 2

ตัวอย่าง

กราฟดังต่อไปนี้เป็นฝ่ายกราฟสมบูรณ์เพราะมีขอบเชื่อมต่อแต่ละจุดสุดยอดจากชุด V ₁แต่ละจุดสุดยอดจากชุด V 2

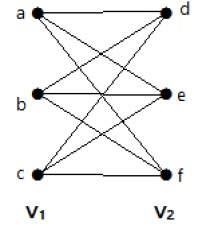
ถ้า | V ₁ | = m และ | V ₂ | n = แล้วฝ่ายกราฟเสร็จสมบูรณ์จะถูกแสดงโดย K _m, n

K _{m, n}มี (m + n) จุดยอดและ (mn) ขอบ
K _{m, n}เป็นกราฟปกติถ้า m = n

โดยทั่วไปก complete bipartite graph is not a complete graph.

K _{m, n}เป็นกราฟที่สมบูรณ์ถ้า m = n = 1

จำนวนขอบสูงสุดในกราฟสองส่วนที่มีจุดยอด n คือ -

[N ² /4]

ถ้า n = 10, K5, 5 = [n 2/4] = [10 ² /4] = 25

ในทำนองเดียวกัน K6, 4 = 24

K7, 3 = 21

K8, 2 = 16

K9, 1 = 9

ถ้า n = 9, k5, 4 = [n2 / 4] = [92/4] = 20

ในทำนองเดียวกัน K6, 3 = 18

K7, 2 = 14

K8, 1 = 8

'G' เป็นกราฟสองส่วนถ้า 'G' ไม่มีรอบของความยาวคี่ กรณีพิเศษของกราฟสองส่วนคือกราฟดาว

สตาร์กราฟ

กราฟสองส่วนที่สมบูรณ์ของรูปแบบ K1, n-1 คือกราฟดาวที่มีจุดยอด n กราฟดาวเป็นกราฟสองส่วนที่สมบูรณ์หากจุดยอดเดียวอยู่ในชุดเดียวและจุดยอดที่เหลือทั้งหมดเป็นของอีกชุดหนึ่ง

ตัวอย่าง

ในกราฟด้านบนจากจุดยอด 'n' จุดยอด 'n – 1' ทั้งหมดเชื่อมต่อกับจุดยอดเดียว ดังนั้นจึงอยู่ในรูปของ K ¹ , ^n-1ซึ่งเป็นกราฟดาว

ส่วนเติมเต็มของกราฟ

ให้ 'G−' เป็นกราฟธรรมดาที่มีจุดยอดบางจุดเหมือนกับ 'G' และขอบ {U, V} อยู่ใน 'G−' ถ้าไม่มีขอบอยู่ใน G หมายความว่าจุดยอดสองจุดอยู่ติดกัน ใน 'G−' ถ้าจุดยอดทั้งสองไม่อยู่ติดกันใน G.

ถ้าขอบที่มีอยู่ในกราฟ I ไม่มีอยู่ในกราฟ II อื่นและถ้าทั้งกราฟ I และกราฟ II ถูกรวมเข้าด้วยกันเพื่อสร้างกราฟที่สมบูรณ์กราฟ I และกราฟ II จะถูกเรียกว่าส่วนเติมเต็มซึ่งกันและกัน

ตัวอย่าง

ในตัวอย่างต่อไปนี้กราฟ - I มีสองขอบ 'cd' และ 'bd' กราฟ -II เสริมของมันมีสี่ขอบ

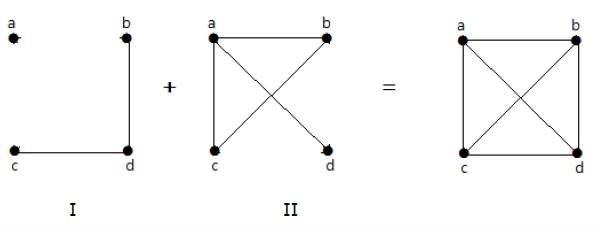
โปรดทราบว่าขอบในกราฟ -I ไม่ปรากฏในกราฟ-II และในทางกลับกัน ดังนั้นการรวมกันของกราฟทั้งสองทำให้ได้กราฟจุดยอด 'n' ที่สมบูรณ์

Note - การรวมกันของกราฟเสริมสองแบบทำให้ได้กราฟที่สมบูรณ์

ถ้า 'G' เป็นกราฟธรรมดา ๆ

| E (G) | + | E ('G -') | = | E (Kn) | โดยที่ n = จำนวนจุดยอดในกราฟ

ตัวอย่าง

ให้ 'G' เป็นกราฟธรรมดาที่มีจุดยอดเก้าจุดและขอบสิบสองด้านให้หาจำนวนขอบใน 'G-'

คุณมี | E (G) | + | E ('G -') | = | E (น) |

12 + | E ('G -') | =

9 (9-1) / 2 = ⁹ C ₂

12 + | E ('G -') | = 36

| E ('G -') | = 24

'G' เป็นกราฟธรรมดาที่มีขอบ 40 ขอบและส่วนเสริม 'G−' มี 38 ขอบ ค้นหาจำนวนจุดยอดในกราฟ G หรือ "G−"

ให้จำนวนจุดยอดในกราฟเป็น 'n'

เรามี, | E (G) | + | E ('G -') | = | E (น) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

ต้นไม้เป็นกราฟที่ไม่มีแม้แต่รอบเดียว แสดงโครงสร้างลำดับชั้นในรูปแบบกราฟิก ต้นไม้อยู่ในคลาสที่ง่ายที่สุดของกราฟ แม้จะมีความเรียบง่าย แต่ก็มีโครงสร้างที่หลากหลาย

ต้นไม้มีแอปพลิเคชั่นที่มีประโยชน์มากมายไม่ว่าจะเป็นแผนผังครอบครัวไปจนถึงต้นไม้ที่ซับซ้อนในโครงสร้างข้อมูลของวิทยาการคอมพิวเตอร์

ต้นไม้

ก connected acyclic graphเรียกว่าต้นไม้ กล่าวอีกนัยหนึ่งกราฟที่เชื่อมต่อโดยไม่มีรอบจะเรียกว่าต้นไม้

ขอบของต้นไม้เรียกว่า branches. องค์ประกอบของต้นไม้เรียกว่าโหนด โหนดที่ไม่มีโหนดลูกจะถูกเรียกleaf nodes.

ต้นไม้ที่มีจุดยอด 'n' มีขอบ 'n-1' ถ้ามันมีขอบมากกว่า 'n-1' อีกหนึ่งขอบที่เห็นได้ชัดควรจะต้องจับคู่กับจุดยอดสองจุดซึ่งนำไปสู่การสร้างวัฏจักร จากนั้นจะกลายเป็นกราฟวัฏจักรซึ่งเป็นการละเมิดกราฟต้นไม้

Example 1

กราฟที่แสดงที่นี่คือต้นไม้เนื่องจากไม่มีรอบและมีการเชื่อมต่อกัน มันมีจุดยอดสี่จุดและสามขอบนั่นคือสำหรับขอบ 'n' จุดยอด 'n-1' ตามที่กล่าวไว้ในคำจำกัดความ

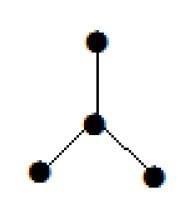
Note - ต้นไม้ทุกต้นมีจุดยอดอย่างน้อยสองจุดในระดับหนึ่ง

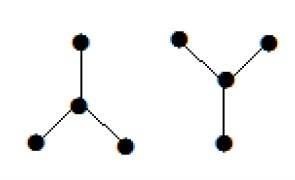
Example 2

ในตัวอย่างข้างต้นจุดยอด 'a' และ 'd' มีระดับหนึ่ง และอีกสองจุดยอด 'b' และ 'c' มีดีกรีสอง เป็นไปได้เพราะหากไม่สร้างวัฏจักรควรมีขอบด้านเดียวอย่างน้อยสองขอบที่ใดก็ได้ในกราฟ มันไม่มีอะไรเลยนอกจากสองขอบที่มีองศาหนึ่ง

ป่าไม้

ก disconnected acyclic graphเรียกว่าป่า กล่าวอีกนัยหนึ่งการรวบรวมต้นไม้ที่ไม่ปะติดปะต่อกันเรียกว่าป่า

Example

กราฟต่อไปนี้ดูเหมือนกราฟย่อยสองกราฟ แต่เป็นกราฟที่ขาดการเชื่อมต่อเพียงเส้นเดียว ไม่มีรอบในกราฟนี้ ดังนั้นเห็นได้ชัดว่ามันเป็นป่า

ต้นไม้ที่ทอดยาว

ให้ G เป็นกราฟที่เชื่อมต่อกันแล้วกราฟย่อย H ของ G เรียกว่าต้นไม้ทอดของ G ถ้า -

H คือต้นไม้
H ประกอบด้วยจุดยอดทั้งหมดของ G.

ต้นไม้ที่ทอด T ของกราฟที่ไม่ได้บอกทิศทาง G คือกราฟย่อยที่มีจุดยอดทั้งหมดของ G

Example

ในตัวอย่างข้างต้น G คือกราฟที่เชื่อมต่อและ H คือกราฟย่อยของ G

เห็นได้ชัดว่ากราฟ H ไม่มีรอบมันเป็นต้นไม้ที่มีขอบหกด้านซึ่งน้อยกว่าจำนวนจุดยอดทั้งหมด ดังนั้น H จึงเป็นต้นไม้ Spanning ของ G.

อันดับวงจร

ให้ 'G' เป็นกราฟที่เชื่อมต่อกับ 'n' จุดยอดและขอบ 'm' ต้นไม้ที่ทอด 'T' ของ G มีขอบ (n-1)

ดังนั้นจำนวนขอบที่คุณต้องลบจาก 'G' เพื่อให้ได้ต้นไม้ที่ขยาย = m- (n-1) ซึ่งเรียกว่าอันดับวงจรของ G

สูตรนี้เป็นจริงเพราะในต้นไม้ที่ทอดคุณต้องมีขอบ 'n-1' จากขอบ 'm' คุณต้องคงขอบ 'n – 1' ไว้ในกราฟ

ดังนั้นการลบขอบ 'n – 1' จาก 'm' จะทำให้ขอบถูกลบออกจากกราฟเพื่อให้ได้ต้นไม้ที่ทอดยาวซึ่งไม่ควรเป็นวัฏจักร

Example

ดูกราฟต่อไปนี้ -

สำหรับกราฟที่ให้ในตัวอย่างข้างต้นคุณมีขอบ m = 7 และจุดยอด n = 5

จากนั้นอันดับวงจรคือ -

G = ม. - (n - 1)

= 7 - (5 - 1)

= 3

Example

ให้ 'G' เป็นกราฟที่เชื่อมต่อกับจุดยอดหกจุดและระดับของจุดยอดแต่ละจุดคือสาม ค้นหาอันดับวงจรของ 'G'

โดยผลรวมของระดับของทฤษฎีบทจุดยอด

n Σ i=1deg (V _i ) = 2 | E |

6 × 3 = 2 | E |

| E | = 9

อันดับวงจร = | E | - (| V | - 1)

= 9 - (6 - 1) = 4

ทฤษฎีบทของ Kirchoff

ทฤษฎีบทของ Kirchoff มีประโยชน์ในการค้นหาจำนวนต้นไม้ที่ทอดยาวซึ่งสามารถสร้างขึ้นจากกราฟที่เชื่อมต่อกัน

Example

เมทริกซ์ 'A' จะถูกเติมเต็มราวกับว่ามีขอบระหว่างจุดยอดสองจุดควรกำหนดเป็น '1', อื่น '0'

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

โดยใช้ทฤษฎีบทของเคิร์ชอฟควรเปลี่ยนเป็นการแทนที่ค่าแนวทแยงหลักด้วยระดับของจุดยอดและองค์ประกอบอื่น ๆ ทั้งหมดด้วย -1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

ดังนั้นจำนวนต้นไม้ที่ทอด = 8

การสำรวจกราฟจากจุดยอดหนึ่งไปยังอีกจุดหนึ่งเป็นไปได้หรือไม่นั้นขึ้นอยู่กับการเชื่อมต่อของกราฟ การเชื่อมต่อเป็นแนวคิดพื้นฐานในทฤษฎีกราฟ การเชื่อมต่อกำหนดว่ากราฟเชื่อมต่อหรือไม่เชื่อมต่อ มีหัวข้อย่อยตามขอบและจุดยอดซึ่งเรียกว่าการเชื่อมต่อขอบและการเชื่อมต่อจุดสุดยอด ให้เราคุยรายละเอียด

การเชื่อมต่อ

กราฟบอกว่าเป็น connected if there is a path between every pair of vertex. จากจุดยอดทุกจุดไปยังจุดยอดอื่น ๆ ควรมีเส้นทางในการสำรวจ ที่เรียกว่าการเชื่อมต่อของกราฟ กราฟที่มีจุดยอดและขอบที่ขาดการเชื่อมต่อหลายจุดถูกตัดการเชื่อมต่อ

Example 1

ในกราฟต่อไปนี้เป็นไปได้ที่จะเดินทางจากจุดยอดหนึ่งไปยังจุดยอดอื่น ๆ ตัวอย่างเช่นเราสามารถข้ามจากจุดยอด 'a' ไปยังจุดยอด 'e' โดยใช้เส้นทาง 'ab-e'

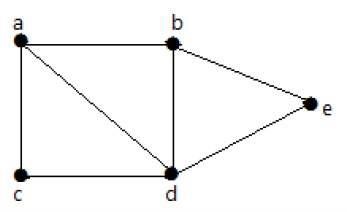
Example 2

ในตัวอย่างต่อไปนี้การข้ามจากจุดยอด 'a' ไปยังจุดยอด 'f' เป็นไปไม่ได้เนื่องจากไม่มีเส้นทางระหว่างทั้งสองโดยตรงหรือโดยอ้อม ดังนั้นจึงเป็นกราฟที่ขาดการเชื่อมต่อ

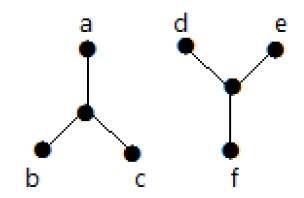
ตัด Vertex

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จุดยอด V ∈ G เรียกว่าจุดยอดตัดของ 'G' ถ้า 'G-V' (ลบ 'V' จาก 'G') ส่งผลให้กราฟขาดการเชื่อมต่อ การลบจุดยอดตัดออกจากกราฟจะแบ่งออกเป็นกราฟสองกราฟขึ้นไป

Note - การลบจุดยอดที่ถูกตัดออกอาจทำให้กราฟขาดการเชื่อมต่อ

กราฟที่เชื่อมต่อ 'G' อาจมีจุดยอดตัดได้มากที่สุด (n – 2)

Example

ในกราฟต่อไปนี้จุดยอด 'e' และ 'c' คือจุดยอดตัด

เมื่อลบ 'e' หรือ 'c' ออกกราฟจะกลายเป็นกราฟที่ไม่เชื่อมต่อ

หากไม่มี 'g' จะไม่มีเส้นทางระหว่างจุดยอด 'c' และจุดยอด 'h' และอื่น ๆ อีกมากมาย ดังนั้นจึงเป็นกราฟที่ตัดการเชื่อมต่อโดยมีจุดยอดตัดเป็น 'e' ในทำนองเดียวกัน 'c' ยังเป็นจุดยอดตัดสำหรับกราฟด้านบน

ตัดขอบ (สะพาน)

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน ขอบ 'e' ∈ G เรียกว่าคมตัดหาก 'G-e' ส่งผลให้กราฟขาดการเชื่อมต่อ

หากการลบขอบในกราฟจะทำให้เกิดกราฟสองกราฟขึ้นไปขอบนั้นจะเรียกว่า Cut Edge

Example

ในกราฟต่อไปนี้ขอบตัดคือ [(c, e)]

การลบขอบ (c, e) ออกจากกราฟจะกลายเป็นกราฟที่ขาดการเชื่อมต่อ

ในกราฟด้านบนการลบขอบ (c, e) จะแบ่งกราฟออกเป็นสองส่วนซึ่งไม่ใช่กราฟที่ไม่มีการเชื่อมต่อ ดังนั้นขอบ (c, e) จึงเป็นขอบตัดของกราฟ

Note - ให้ 'G' เป็นกราฟที่เชื่อมต่อกับจุดยอด 'n' แล้ว

ขอบตัด e ∈ G ถ้าขอบ 'e' ไม่ได้เป็นส่วนหนึ่งของวงจรใด ๆ ใน G
จำนวนคมตัดสูงสุดที่ทำได้คือ 'n-1'
เมื่อใดก็ตามที่มีขอบตัดจะมีจุดยอดตัดด้วยเนื่องจากจุดยอดของขอบตัดอย่างน้อยหนึ่งจุดเป็นจุดยอดตัด
หากมีจุดยอดตัดอยู่อาจมีหรือไม่มีคมตัดก็ได้

ตัดชุดกราฟ

ให้ 'G' = (V, E) เป็นกราฟที่เชื่อมต่อ ชุดย่อย E 'ของ E เรียกว่าชุดตัดของ G หากการลบขอบทั้งหมดของ E' ออกจาก G จะทำให้ G ตัดการเชื่อมต่อ

หากการลบขอบจำนวนหนึ่งออกจากกราฟทำให้ขาดการเชื่อมต่อขอบที่ถูกลบเหล่านั้นจะเรียกว่าชุดตัดของกราฟ

Example

ดูกราฟต่อไปนี้ ชุดตัดคือ E1 = {e1, e3, e5, e8}

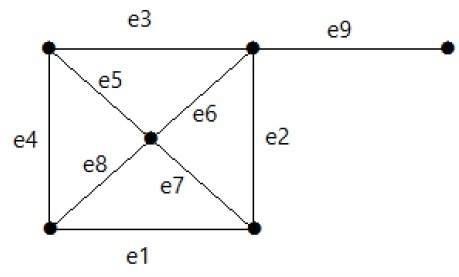
หลังจากลบชุดตัด E1 ออกจากกราฟแล้วจะปรากฏดังนี้ -

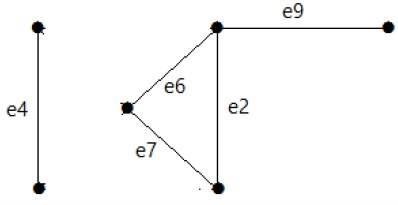
ในทำนองเดียวกันมีชุดตัดอื่น ๆ ที่สามารถตัดการเชื่อมต่อของกราฟได้ -

E3 = {e9} - ชุดตัดที่เล็กที่สุดของกราฟ
E4 = {e3, e4, e5}

การเชื่อมต่อ Edge

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จำนวนขอบขั้นต่ำที่การลบทำให้ตัดการเชื่อมต่อ 'G' เรียกว่าการเชื่อมต่อขอบของ G

Notation - λ (G)

กล่าวอีกนัยหนึ่งคือ number of edges in a smallest cut set of G เรียกว่าการเชื่อมต่อขอบของ G.

ถ้า 'G' มีคมตัดแล้วλ (G) คือ 1 (การเชื่อมต่อขอบของ G)

Example

ดูกราฟต่อไปนี้ การลบขอบขั้นต่ำสองเส้นออกทำให้กราฟที่เชื่อมต่อขาดการเชื่อมต่อ ดังนั้นการเชื่อมต่อแบบ edge (λ (G)) คือ 2

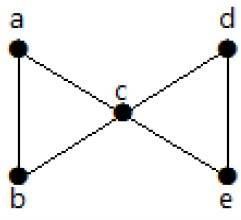
ต่อไปนี้คือสี่วิธีในการตัดการเชื่อมต่อของกราฟโดยการลบสองขอบ -

การเชื่อมต่อ Vertex

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จำนวนจุดต่ำสุดที่การลบทำให้ 'G' ถูกตัดการเชื่อมต่อหรือลด 'G' ในกราฟเล็กน้อยเรียกว่าการเชื่อมต่อจุดยอด

Notation - เค (G)

Example

ในกราฟด้านบนการลบจุดยอด 'e' และ 'i' ทำให้กราฟถูกตัดการเชื่อมต่อ

ถ้า G มีจุดยอดตัดแล้ว K (G) = 1

Notation - สำหรับกราฟ G ที่เชื่อมต่อใด ๆ

K (G) ≤λ (G) ≤δ (G)

การเชื่อมต่อจุดยอด (K (G)) การเชื่อมต่อที่ขอบ (λ (G)) จำนวนองศาขั้นต่ำของ G (δ (G))

Example

คำนวณλ (G) และ K (G) สำหรับกราฟต่อไปนี้ -

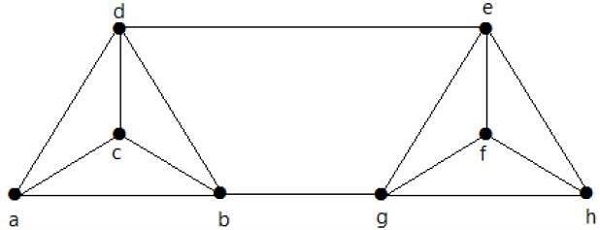
Solution

จากกราฟ

δ (G) = 3

K (G) ≤λ (G) ≤δ (G) = 3 (1)

K (G) ≥ 2 (2)

การลบขอบ {d, e} และ {b, h} เราสามารถตัดการเชื่อมต่อ G

ดังนั้น,

λ (G) = 2

2 ≤λ (G) ≤δ (G) = 2 (3)

จาก (2) และ (3) จุดยอดการเชื่อมต่อ K (G) = 2

กราฟที่ครอบคลุมคือกราฟย่อยที่มีจุดยอดทั้งหมดหรือขอบทั้งหมดที่ตรงกับกราฟอื่น ๆ ย่อหน้าย่อยที่มีจุดยอดทั้งหมดเรียกว่า aline/edge covering. กราฟย่อยที่มีขอบทั้งหมดเรียกว่าไฟล์vertex covering.

การครอบคลุมเส้น

ให้ G = (V, E) เป็นกราฟ เซตย่อย C (E) เรียกว่าเส้นที่ครอบคลุม G ถ้าทุกจุดยอดของ G เกิดขึ้นโดยมีอย่างน้อยหนึ่งขอบใน C นั่นคือ

องศา (V) ≥ 1 ∀ V ∈ G

เนื่องจากจุดยอดแต่ละจุดเชื่อมต่อกับจุดยอดอื่นด้วยขอบ ดังนั้นจึงมีระดับขั้นต่ำ 1

Example

ดูกราฟต่อไปนี้ -

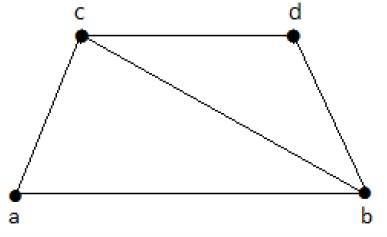
ย่อหน้าที่มีเส้นครอบคลุมมีดังนี้ -

ค₁ = {{a, b}, {c, d}}

ค₂ = {{a, d}, {b, c}}

ค₃ = {{a, b}, {b, c}, {b, d}}

ค₄ = {{a, b}, {b, c}, {c, d}}

ไม่มีการปิดทับบรรทัดของ 'G' ก็ต่อเมื่อ 'G' มีจุดยอดที่แยกได้ เส้นคลุมของกราฟที่มีจุดยอด 'n' มีขอบอย่างน้อย [n / 2]

การครอบคลุมบรรทัดน้อยที่สุด

เส้นที่ครอบคลุม C ของกราฟ G มีค่าน้อยที่สุด if no edge can be deleted from C.

Example

ในกราฟด้านบนกราฟย่อยที่มีเส้นครอบคลุมมีดังนี้ -

ค₁ = {{a, b}, {c, d}}

ค₂ = {{a, d}, {b, c}}

ค₃ = {{a, b}, {b, c}, {b, d}}

ค₄ = {{a, b}, {b, c}, {c, d}}

ในที่นี้ C ₁ , C ₂ , C ₃เป็นการปิดทับเส้นขั้นต่ำในขณะที่ C ₄ไม่ใช่เพราะเราสามารถลบ {b, c} ได้

การครอบคลุมบรรทัดขั้นต่ำ

เป็นที่รู้จักกันในชื่อ Smallest Minimal Line Covering. เส้นขั้นต่ำที่มีจำนวนขอบขั้นต่ำเรียกว่าเส้นขั้นต่ำที่ครอบคลุม 'G' จำนวนขอบในเส้นขั้นต่ำที่ครอบคลุมใน 'G' เรียกว่าline covering numberของ 'G' (α ₁ )

Example

ในตัวอย่างข้างต้น C ₁และ C ₂คือเส้นคลุมขั้นต่ำของ G และα ₁ = 2

การครอบคลุมทุกบรรทัดมีการปิดบรรทัดน้อยที่สุด
การครอบคลุมทุกบรรทัดไม่มีการปิดบรรทัดขั้นต่ำ (C ₃ไม่มีการครอบคลุมบรรทัดขั้นต่ำ
ไม่มีการครอบคลุมบรรทัดขั้นต่ำที่ประกอบด้วยวัฏจักร
หากเส้นที่ครอบคลุม "C" ไม่มีเส้นทางที่มีความยาวตั้งแต่ 3 ขึ้นไป "C" จะเป็นเส้นเล็ก ๆ ที่ครอบคลุมเนื่องจากส่วนประกอบทั้งหมดของ "C" เป็นกราฟดาวและจากกราฟดาวจะไม่สามารถลบขอบได้

เวอร์เท็กซ์ครอบคลุม

ให้ 'G' = (V, E) เป็นกราฟ เซตย่อย K ของ V เรียกว่าจุดยอดที่ครอบคลุม 'G' ถ้าขอบทุกด้านของ 'G' เกิดขึ้นกับหรือปิดทับด้วยจุดยอดใน 'K'

Example

ดูกราฟต่อไปนี้ -

กราฟย่อยที่ได้มาจากกราฟด้านบนมีดังนี้ -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

ที่นี่ K ₁ K ₂และ K ₃มีจุดยอดครอบคลุมในขณะที่ K ₄ไม่มีจุดยอดครอบคลุมเนื่องจากไม่ครอบคลุมขอบ {bc}

ครอบคลุมจุดยอดน้อยที่สุด

จุดยอด 'K' ของกราฟ 'G' ถูกกล่าวว่าเป็นจุดยอดขั้นต่ำที่ครอบคลุมหากไม่สามารถลบจุดยอดออกจาก 'K' ได้

Example

ในกราฟด้านบนกราฟย่อยที่มีจุดยอดครอบคลุมมีดังนี้ -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

ในที่นี้ K ₁และ K ₂เป็นการปกปิดจุดยอดน้อยที่สุดในขณะที่ K ₃จุดยอด 'd' สามารถลบได้

การครอบคลุมจุดยอดขั้นต่ำ

เป็นที่รู้จักกันว่าเป็นจุดยอดน้อยที่สุดที่ครอบคลุม จุดยอดขั้นต่ำที่ครอบคลุมกราฟ 'G' ที่มีจำนวนจุดยอดต่ำสุดเรียกว่าจุดยอดต่ำสุดที่ครอบคลุม

จำนวนจุดยอดในจุดยอดต่ำสุดที่ครอบคลุม 'G' เรียกว่าจุดยอดครอบคลุมจำนวน G (α ₂ )

Example

ในกราฟต่อไปนี้กราฟย่อยที่มีจุดยอดครอบคลุมมีดังนี้ -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

ในที่นี้ K ₁คือจุดยอดขั้นต่ำของ G เนื่องจากมีจุดยอดเพียงสองจุด α ₂ = 2

กราฟที่ตรงกันคือกราฟย่อยของกราฟที่ไม่มีขอบติดกัน เพียงแค่ไม่ควรมีจุดยอดทั่วไประหว่างสองขอบใด ๆ

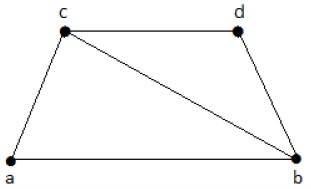
การจับคู่

ให้ 'G' = (V, E) เป็นกราฟ กราฟย่อยเรียกว่า M (G) ที่ตรงกันif each vertex of G is incident with at most one edge in Mกล่าวคือ

องศา (V) ≤ 1 ∀ V ∈ G

ซึ่งหมายความว่าในกราฟที่ตรงกัน M (G) จุดยอดควรมีระดับ 1 หรือ 0 โดยที่ขอบควรจะตกจากกราฟ G

Notation - ม (G)

Example

ในการจับคู่

ถ้า deg (V) = 1 ดังนั้น (V) จะบอกว่าตรงกัน

ถ้า deg (V) = 0 แสดงว่า (V) ไม่ตรงกัน

ในการจับคู่ไม่มีขอบสองด้านติดกัน เป็นเพราะถ้าสองขอบใด ๆ อยู่ติดกันดังนั้นระดับของจุดยอดที่เชื่อมขอบทั้งสองนั้นจะมีระดับ 2 ซึ่งละเมิดกฎการจับคู่

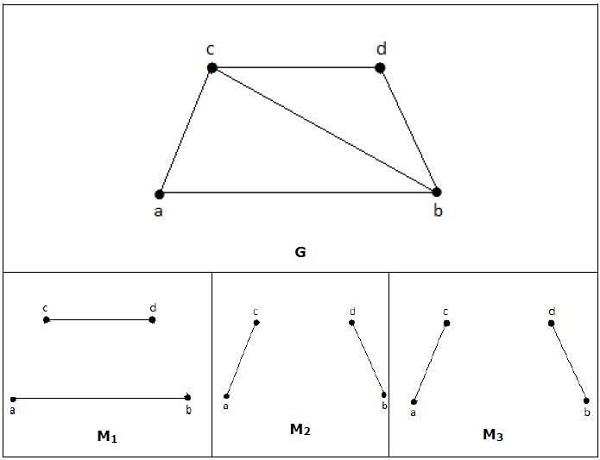
การจับคู่สูงสุด

M ที่ตรงกันของกราฟ 'G' ถูกกล่าวว่ามีค่าสูงสุด if no other edges of ‘G’ can be added to M.

Example

M1, M2, M3 จากกราฟด้านบนเป็นการจับคู่สูงสุดของ G

การจับคู่สูงสุด

เรียกอีกอย่างว่าการจับคู่สูงสุดที่ใหญ่ที่สุด การจับคู่สูงสุดถูกกำหนดให้เป็นการจับคู่สูงสุดกับจำนวนขอบสูงสุด

จำนวนขอบในการจับคู่สูงสุดของ 'G' เรียกว่ามัน matching number.

Example

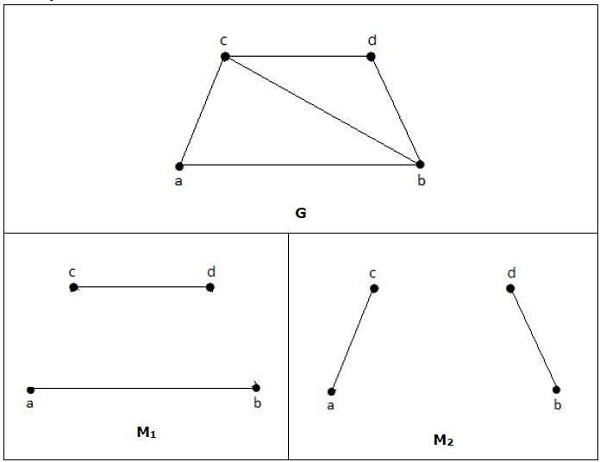
สำหรับกราฟที่ให้ในตัวอย่างข้างต้น M1 และ M2 เป็นการจับคู่สูงสุดของ 'G' และจำนวนที่ตรงกันคือ 2 ดังนั้นด้วยการใช้กราฟ G เราสามารถสร้างกราฟย่อยที่มีขอบสูงสุดเพียง 2 ขอบเท่านั้น ดังนั้นเราจึงมีหมายเลขที่ตรงกันเป็นสอง

การจับคู่ที่สมบูรณ์แบบ

การจับคู่ (M) ของกราฟ (G) ถูกกล่าวว่าเป็นการจับคู่ที่สมบูรณ์แบบหากทุกจุดยอดของกราฟ g (G) เกิดขึ้นกับขอบด้านหนึ่งของการจับคู่ (M) นั่นคือ

องศา (V) = 1 ∀ V

ระดับของจุดยอดแต่ละจุดในกราฟย่อยควรมีระดับ 1

Example

ในกราฟต่อไปนี้ M1 และ M2 เป็นตัวอย่างของการจับคู่ G ที่สมบูรณ์แบบ

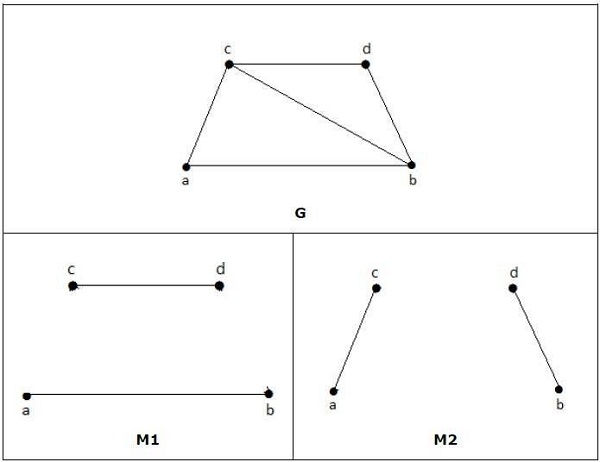
Note - การจับคู่กราฟที่สมบูรณ์แบบทุกครั้งยังเป็นการจับคู่กราฟสูงสุดเนื่องจากไม่มีโอกาสเพิ่มขอบอีกหนึ่งเส้นในกราฟการจับคู่ที่สมบูรณ์แบบ

การจับคู่กราฟสูงสุดไม่จำเป็นต้องสมบูรณ์แบบ หากกราฟ 'G' มีค่าที่ตรงกันจำนวนจุดยอด | V (G) | เป็นคู่ ถ้าเป็นเลขคี่จุดยอดสุดท้ายจะจับคู่กับจุดยอดอื่นและสุดท้ายก็ยังคงมีจุดยอดเดียวที่ไม่สามารถจับคู่กับจุดยอดอื่นใดที่มีองศาเป็นศูนย์ มันละเมิดหลักการจับคู่ที่สมบูรณ์แบบอย่างชัดเจน

Example

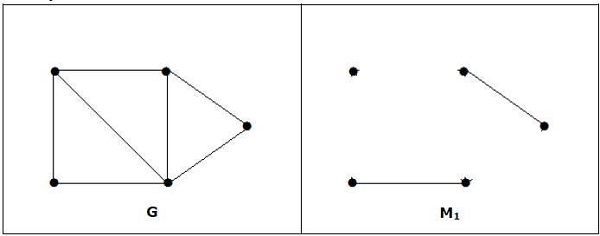
Note- การสนทนาของข้อความข้างต้นไม่จำเป็นต้องเป็นความจริง ถ้า G มีจำนวนจุดยอดเท่ากัน M1 ก็ไม่จำเป็นต้องสมบูรณ์แบบ

Example

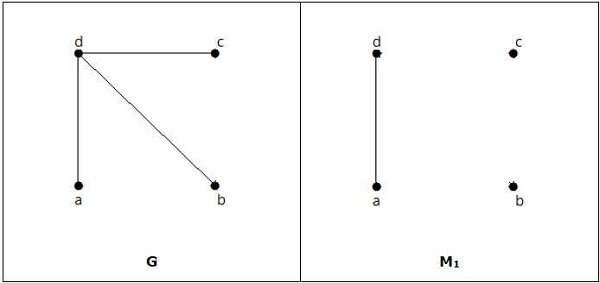
มันตรงกัน แต่ไม่ใช่การจับคู่ที่สมบูรณ์แบบแม้ว่าจะมีจำนวนจุดยอด

เซตอิสระจะแสดงเป็นเซตซึ่ง

ไม่ควรมี any edges adjacent to each other. ไม่ควรมีจุดยอดทั่วไประหว่างสองขอบใด ๆ
ไม่ควรมี any vertices adjacent to each other. ไม่ควรมีขอบทั่วไประหว่างจุดยอดทั้งสอง

ชุดสายอิสระ

ให้ 'G' = (V, E) เป็นกราฟ ส่วนย่อย L ของ E เรียกว่าชุดบรรทัดอิสระของ 'G' หากไม่มีขอบสองด้านใน L อยู่ติดกัน ชุดดังกล่าวเรียกว่าชุดสายอิสระ

Example

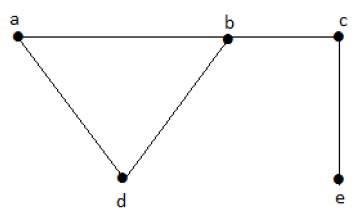
ให้เราพิจารณาส่วนย่อยต่อไปนี้ -

L₁ = {a,b}
L₂ = {a,b} {c,e}
L₃ = {a,d} {b,c}

ในตัวอย่างนี้ส่วนย่อย L2 และ L3 ไม่ใช่ขอบที่อยู่ติดกันในกราฟที่กำหนดอย่างชัดเจน เป็นชุดสายอิสระ อย่างไรก็ตาม L1 ไม่ใช่ชุดเส้นอิสระสำหรับการสร้างชุดเส้นอิสระควรมีอย่างน้อยสองขอบ

ชุดเส้นอิสระสูงสุด

ชุดเส้นอิสระถูกกล่าวว่าเป็นชุดเส้นอิสระสูงสุดของกราฟ 'G' ถ้าไม่สามารถเพิ่มขอบอื่นของ 'G' ใน 'L' ได้

Example

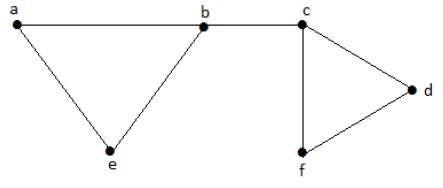
ให้เราพิจารณาส่วนย่อยต่อไปนี้ -

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L ₂และ L ₃เป็นชุดเส้นอิสระสูงสุด / การจับคู่สูงสุด สำหรับเพียงสองส่วนย่อยนี้ไม่มีโอกาสเพิ่มขอบอื่นใดที่ไม่ใช่ส่วนที่อยู่ติดกัน ดังนั้นทั้งสองส่วนย่อยจึงถือเป็นชุดบรรทัดอิสระสูงสุด

ชุดสายอิสระสูงสุด

ชุดเส้นอิสระสูงสุดของ 'G' ที่มีจำนวนขอบสูงสุดเรียกว่าชุดเส้นอิสระสูงสุด 'G'

Number of edges in a maximum independent line set of G (β₁)
   = Line independent number of G
   = Matching number of G

Example

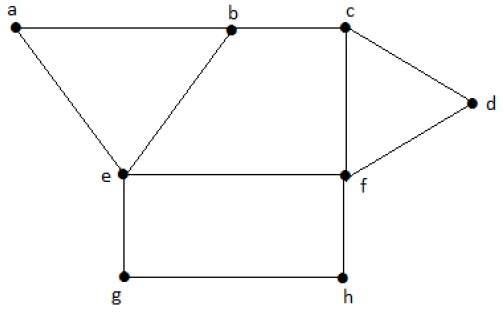
ให้เราพิจารณาส่วนย่อยต่อไปนี้ -

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L ₃คือชุดเส้นอิสระสูงสุดของ G ที่มีขอบสูงสุดซึ่งไม่ใช่ขอบที่อยู่ติดกันในกราฟและแสดงด้วยβ1 = 3

Note - สำหรับกราฟ G ใด ๆ ที่ไม่มีจุดยอดแยก

α1 + β1 = จำนวนจุดยอดในกราฟ = | V |

Example

บรรทัดครอบคลุมจำนวน K _n / C _n / w _n ,

$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$

หมายเลขอิสระของเส้น (หมายเลขที่ตรงกัน) = β ₁ = [n / 2] α ₁ + β ₁ = n

ชุดจุดยอดอิสระ

ให้ 'G' = (V, E) เป็นกราฟ ชุดย่อยของ 'V' เรียกว่าชุดอิสระของ 'G' หากไม่มีจุดยอดสองจุดใน 'S' อยู่ติดกัน

Example

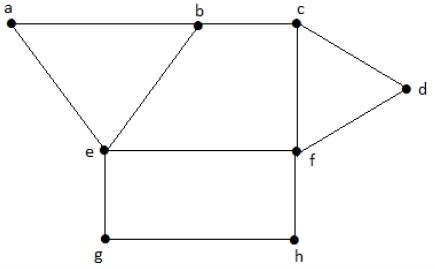
พิจารณาชุดย่อยต่อไปนี้จากกราฟด้านบน -

S₁ = {e}

S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

เห็นได้ชัดว่า S ₁ไม่ใช่เซตจุดยอดอิสระเนื่องจากในการรับเซตจุดยอดอิสระควรมีจุดยอดอย่างน้อยสองจุดในกราฟจากกราฟ แต่ที่นี่ไม่เป็นเช่นนั้น เซ็ตย่อย S ₂ , S ₃และ S ₄เป็นเซตจุดยอดอิสระเนื่องจากไม่มีจุดยอดที่อยู่ติดกับจุดยอดใดจุดยอดหนึ่งจากเซตย่อย

ชุดจุดยอดอิสระสูงสุด

ให้ 'G' เป็นกราฟจากนั้นชุดจุดยอดอิสระของ 'G' จะถูกกล่าวว่าสูงสุดหากไม่สามารถเพิ่มจุดยอดอื่นของ 'G' ใน 'S' ได้

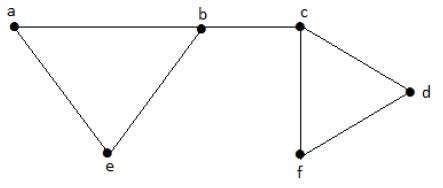
Example

พิจารณาส่วนย่อยต่อไปนี้จากกราฟด้านบน

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

S ₂และ S ₃เป็นชุดจุดยอดอิสระสูงสุดของ 'G' ใน S ₁และ S ₄เราสามารถเพิ่มจุดยอดอื่น ๆ แต่ใน S ₂และ S ₃เราไม่สามารถเพิ่มจุดยอดอื่นได้

ชุดจุดยอดอิสระสูงสุด

ชุดจุดยอดอิสระสูงสุดของ 'G' ที่มีจำนวนจุดยอดสูงสุดเรียกว่าชุดจุดยอดอิสระสูงสุด

Example

พิจารณาชุดย่อยต่อไปนี้จากกราฟด้านบน -

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

เฉพาะ S ₃เท่านั้นที่เป็นชุดจุดยอดอิสระสูงสุดเนื่องจากครอบคลุมจุดยอดสูงสุดจำนวนมาก จำนวนจุดยอดในชุดจุดยอดอิสระสูงสุดของ 'G' เรียกว่าจำนวนจุดยอดอิสระของ G (β ₂ )

Example

สำหรับฉบับสมบูรณ์กราฟ K _n ,

จุดยอดครอบคลุมจำนวน = α ₂ = n − 1

จำนวนอิสระจุดยอด = β ₂ = 1

คุณมีα ₂ + β ₂ = n

ในกราฟที่สมบูรณ์จุดยอดแต่ละจุดอยู่ติดกับจุดยอดที่เหลือ (n - 1) ดังนั้นชุดอิสระสูงสุดของ K _{n จึง}มีจุดยอดเพียงจุดเดียว

ดังนั้นβ ₂ = 1

และα ₂ = | v | - β ₂ = n-1

Note - สำหรับกราฟ 'G' = (V, E)

α ₂ + β ₂ = | v |
ถ้า 'S' เป็นชุดจุดยอดอิสระของ 'G' ดังนั้น (V - S) จะเป็นจุดยอดปกของ G

การระบายสีกราฟไม่ได้เป็นเพียงวิธีง่ายๆในการติดฉลากส่วนประกอบของกราฟเช่นจุดยอดขอบและพื้นที่ภายใต้ข้อ จำกัด บางประการ ในกราฟไม่มีจุดยอดสองจุดที่อยู่ติดกันขอบที่อยู่ติดกันหรือบริเวณที่อยู่ติดกันจะถูกระบายสีด้วยจำนวนสีขั้นต่ำ หมายเลขนี้เรียกว่าchromatic number และกราฟเรียกว่า a properly colored graph.

ในขณะที่การระบายสีกราฟข้อ จำกัด ที่กำหนดไว้บนกราฟ ได้แก่ สีลำดับของการระบายสีวิธีการกำหนดสี ฯลฯ การระบายสีจะถูกกำหนดให้กับจุดยอดหรือพื้นที่เฉพาะ ดังนั้นจุดยอดหรือพื้นที่ที่มีสีเดียวกันจึงสร้างชุดอิสระ

Vertex ระบายสี

การระบายสีจุดยอดคือการกำหนดสีให้กับจุดยอดของกราฟ 'G' เพื่อให้ไม่มีจุดยอดสองจุดที่อยู่ติดกันมีสีเดียวกัน พูดง่ายๆคือไม่ควรมีจุดยอดสองจุดของขอบที่มีสีเดียวกัน

Chromatic Number

จำนวนสีขั้นต่ำที่จำเป็นสำหรับการระบายสีจุดสุดยอดของกราฟ 'G' เรียกว่าเป็นจำนวนสีของ G ซึ่งแสดงด้วย X (G)

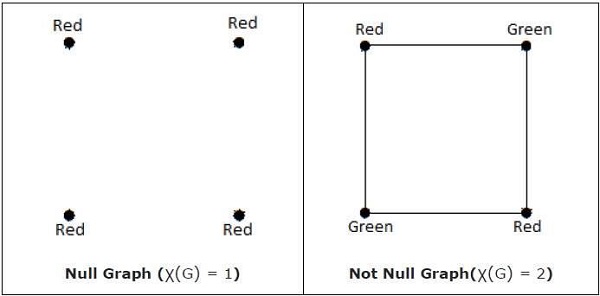
χ (G) = 1 ถ้า 'G' เป็นกราฟว่าง ถ้า 'G' ไม่ใช่กราฟว่างดังนั้นχ (G) ≥ 2

Example

Note - กราฟ 'G' ถูกกล่าวว่าเป็น n-coverable หากมีจุดยอดสีที่ใช้สีมากที่สุด n สีเช่น X (G) ≤ n

ภูมิภาคระบายสี

การระบายสีพื้นที่คือการกำหนดสีให้กับพื้นที่ของกราฟระนาบเพื่อให้ไม่มีพื้นที่ติดกันสองแห่งที่มีสีเหมือนกัน กล่าวกันว่าภูมิภาคสองแห่งอยู่ติดกันหากมีขอบร่วมกัน

Example

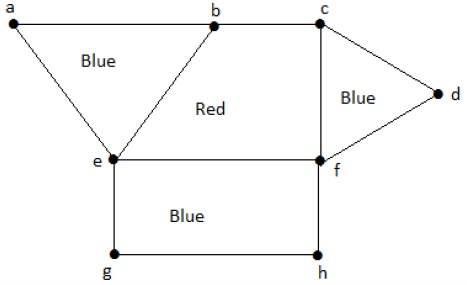
ดูกราฟต่อไปนี้ ภูมิภาค 'aeb' และ 'befc' อยู่ติดกันเนื่องจากมี 'be' ร่วมกันระหว่างภูมิภาคทั้งสอง

ในทำนองเดียวกันภูมิภาคอื่น ๆ จะมีสีตามความเหมาะสม กราฟนี้มีสีดังนี้ -

Example

จำนวนสีของ Kn คือ

n
n–1
[n/2]
[n/2]

ลองพิจารณาตัวอย่างนี้กับภาคที่ 4

ในกราฟที่สมบูรณ์จุดยอดแต่ละจุดอยู่ติดกับจุดยอดที่เหลือ (n - 1) ดังนั้นจุดยอดแต่ละจุดจึงต้องใช้สีใหม่ ดังนั้นจำนวนสีของ K _n = n

แอพพลิเคชั่นระบายสีกราฟ

การระบายสีกราฟเป็นแนวคิดที่สำคัญที่สุดอย่างหนึ่งในทฤษฎีกราฟ ใช้ในการประยุกต์ใช้วิทยาการคอมพิวเตอร์แบบเรียลไทม์เช่น -

Clustering
การขุดข้อมูล
การจับภาพ
การแบ่งส่วนภาพ
Networking
การจัดสรรทรัพยากร
การจัดกำหนดการกระบวนการ

กราฟสามารถมีอยู่ในรูปแบบต่างๆโดยมีจำนวนจุดยอดขอบและการเชื่อมต่อขอบเดียวกัน กราฟดังกล่าวเรียกว่ากราฟไอโซมอร์ฟิก โปรดทราบว่าเราติดป้ายกำกับกราฟในบทนี้เป็นหลักเพื่อจุดประสงค์ในการอ้างอิงถึงกราฟและจดจำกราฟจากกันและกัน

กราฟ Isomorphic

กราฟสองกราฟ G ₁และ G ₂ถูกกล่าวว่าเป็นไอโซมอร์ฟิกถ้า -

จำนวนส่วนประกอบ (จุดยอดและขอบ) เหมือนกัน
การเชื่อมต่อแบบ edge จะยังคงอยู่

Note- ในระยะสั้นจากกราฟไอโซมอร์ฟิกสองกราฟอันหนึ่งเป็นกราฟที่ปรับแต่งแล้วของอีกกราฟ กราฟที่ไม่มีป้ายกำกับสามารถคิดได้ว่าเป็นกราฟไอโซมอร์ฟิก

There exists a function ‘f’ from vertices of G₁ to vertices of G₂
   [f: V(G₁) ⇒ V(G₂)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G₁, then the
edge {f(U), f(V)} ∈ G₂, then G₁ ≡ G₂.

Note

ถ้า G ₁ ≡ G ₂แล้ว -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

ลำดับองศาของ G ₁และ G ₂เหมือนกัน

ถ้าจุดยอด {V ₁ , V ₂ , .. Vk} เป็นวัฏจักรของความยาว K ใน G ₁ดังนั้นจุดยอด {f (V ₁ ), f (V ₂ ), … f (Vk)} ควรเป็นวัฏจักร ความยาว K จี2

เงื่อนไขทั้งหมดข้างต้นจำเป็นสำหรับกราฟ G ₁และ G ₂เป็นไอโซมอร์ฟิก แต่ไม่เพียงพอที่จะพิสูจน์ว่ากราฟนั้นเป็นไอโซมอร์ฟิก

(G ₁ ≡ G ₂ ) ถ้า (G ₁ - ≡ G ₂ -) เท่านั้นโดยที่ G ₁และ G ₂เป็นกราฟธรรมดา
(G ₁ ≡ G ₂ ) ถ้าเมทริกซ์ adjacency ของ G ₁และ G ₂เหมือนกัน
(G ₁ ≡ G ₂ ) ก็ต่อเมื่อกราฟย่อยที่เกี่ยวข้องของ G ₁และ G ₂ (ได้จากการลบจุดยอดบางจุดใน G1 และรูปภาพในกราฟ G ₂ ) เป็นไอโซมอร์ฟิก

Example

กราฟใดต่อไปนี้เป็นไอโซมอร์ฟิก

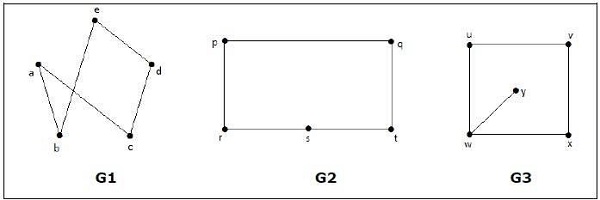
ในรูปแบบของกราฟ G ₃ , จุดสุดยอด 'w' มีเพียงระดับ 3 ในขณะที่ทุกจุดกราฟอื่น ๆ ที่มีการศึกษาระดับปริญญา 2. ดังนั้น G3 ไม่ isomorphic ถึง G ₁หรือ G 2

การเติมเต็ม G ₁และ G ₂คุณมี -

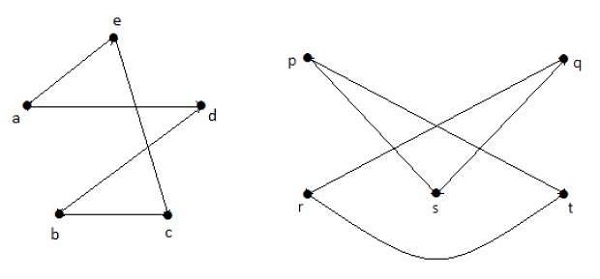
ที่นี่ (G ₁ - ≡ G ₂ -) ดังนั้น (G ₁ ≡ G ₂ )

กราฟระนาบ

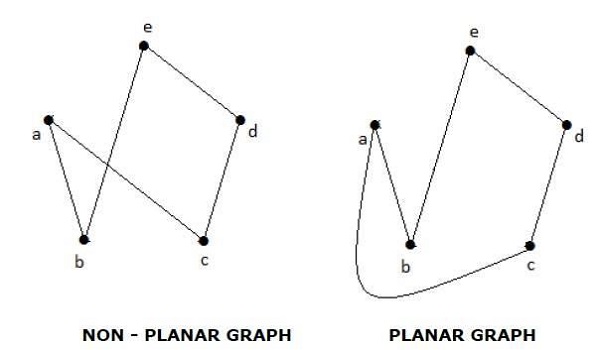
กราฟ 'G' จะถูกกล่าวว่าเป็นระนาบหากสามารถวาดบนระนาบหรือทรงกลมเพื่อไม่ให้ขอบทั้งสองด้านตัดกันที่จุดที่ไม่ใช่จุดยอด

Example

ภูมิภาค

กราฟระนาบทุกเส้นแบ่งระนาบออกเป็นพื้นที่เชื่อมต่อกันเรียกว่าพื้นที่

Example

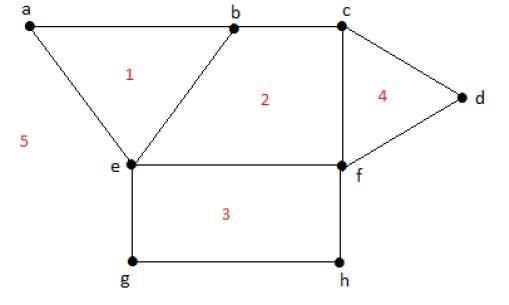
ระดับของภูมิภาคที่มีขอบเขต r = deg(r) = จำนวนขอบที่ล้อมรอบพื้นที่ r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8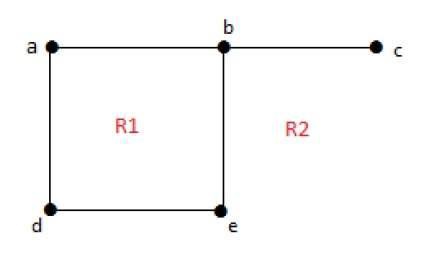

ระดับของภูมิภาคที่ไม่มีขอบเขต r = deg(r) = จำนวนขอบที่ล้อมรอบพื้นที่ r.

deg(R₁) = 4
deg(R₂) = 6

ในกราฟระนาบคุณสมบัติต่อไปนี้ถือเป็นสิ่งที่ดี -

ในกราฟระนาบที่มีจุดยอด 'n' ผลรวมขององศาของจุดยอดทั้งหมดคือ -

n Σ i = 1 องศา (V _i ) = 2 | E |

ตาม Sum of Degrees of Regions/ ทฤษฎีบทในกราฟระนาบที่มีพื้นที่ 'n' ผลรวมขององศาของพื้นที่คือ -

n Σ i = 1 องศา (ริ) = 2 | E |

จากทฤษฎีบทข้างต้นคุณสามารถสรุปได้ดังนี้ -

ในกราฟระนาบ

ถ้าองศาของแต่ละภูมิภาคคือ K ผลรวมขององศาของพื้นที่คือ -

K | R | = 2 | E |

หากระดับของแต่ละภูมิภาคมีค่าอย่างน้อย K (≥ K) ดังนั้น

K | R | ≤ 2 | E |

หากระดับของแต่ละภูมิภาคมีค่ามากที่สุด K (≤ K) ดังนั้น

K | R | ≥ 2 | E |

Note - สมมติว่าทุกภูมิภาคมีระดับเดียวกัน

ตาม Euler’s Formulae บนกราฟระนาบ

หากกราฟ 'G' เป็นระนาบที่เชื่อมต่อกันแล้ว

| V | + | R | = | E | + 2

หากกราฟระนาบที่มีส่วนประกอบ 'K' แล้ว

| V | + | R | = | E | + (K + 1)

ที่ไหน, | V | คือจำนวนจุดยอด | E | คือจำนวนขอบและ | R | คือจำนวนภูมิภาค

Edge Vertex Inequality

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อโดยมีระดับของแต่ละภูมิภาคอย่างน้อย 'K'

| E | ≤ k / (k-2) {| v | - 2}

รู้ไหม | V | + | R | = | E | + 2

พ. | ร | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อแบบธรรมดาดังนั้น

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

มีจุดยอด V •∈ G อย่างน้อยหนึ่งจุดซึ่ง deg (V) ≤ 5

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อกันอย่างง่าย (มีขอบอย่างน้อย 2 ขอบ) และไม่มีสามเหลี่ยม

|E| ≤ {2|V| – 4}

ทฤษฎีบทของ Kuratowski

กราฟ 'G' ไม่เป็นระนาบเดียวและถ้าหาก 'G' มี subgraph ซึ่งเป็นมอร์ฟิคที่จะเค₅หรือ K 3,3

Homomorphism

กราฟสองกราฟ G ₁และ G ₂ถูกกล่าวว่าเป็นโฮโมมอร์ฟิกถ้ากราฟแต่ละกราฟเหล่านี้สามารถหาได้จากกราฟ 'G' เดียวกันโดยการหารขอบบางส่วนของ G ด้วยจุดยอดที่มากกว่า ดูตัวอย่างต่อไปนี้ -

แบ่งขอบ 'rs' ออกเป็นสองขอบโดยเพิ่มจุดยอดหนึ่งจุด

กราฟที่แสดงด้านล่างเป็นโฮโมมอร์ฟิกกับกราฟแรก

ถ้า G ₁เป็น isomorphic ถึง G ₂ดังนั้น G จะเป็น homeomorphic ถึง G2 แต่การสนทนาไม่จำเป็นต้องเป็นจริง

กราฟใด ๆ ที่มีจุดยอด 4 จุดหรือน้อยกว่าจะเป็นแนวระนาบ
กราฟใด ๆ ที่มีขอบ 8 หรือน้อยกว่าจะเป็นแนวระนาบ
กราฟสมบูรณ์ K _nคือระนาบถ้า n ≤ 4 เท่านั้น
กราฟสองส่วนที่สมบูรณ์ K _{m, n}เป็นระนาบถ้า m ≤ 2 หรือ n ≤ 2 เท่านั้น
กราฟไม่ใช่ภาพถ่ายที่เรียบง่ายด้วยจำนวนขั้นต่ำของจุดมีความสมบูรณ์แบบของกราฟ K 5
กราฟง่ายไม่ใช่ภาพถ่ายที่มีจำนวนขั้นต่ำของขอบเป็น K _3,3

กราฟหลายเหลี่ยม

กราฟระนาบที่เชื่อมต่ออย่างง่ายเรียกว่ากราฟรูปหลายเหลี่ยมหากระดับของจุดยอดแต่ละจุดมีค่า≥ 3 นั่นคือ deg (V) ≥ 3 ∀ V ∈ G

3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |

กราฟสามารถข้ามผ่านได้หากคุณสามารถวาดเส้นทางระหว่างจุดยอดทั้งหมดโดยไม่ต้องย้อนเส้นทางเดิม จากเส้นทางนี้มีบางประเภทเช่นเส้นทางของออยเลอร์และวงจรของออยเลอร์ซึ่งอธิบายไว้ในบทนี้

เส้นทางของออยเลอร์

เส้นทางของออยเลอร์มีขอบแต่ละด้านของ 'G' หนึ่งครั้งและแต่ละจุดยอดของ 'G' อย่างน้อยหนึ่งครั้ง กราฟที่เชื่อมต่อ G ถูกกล่าวว่าสามารถข้ามผ่านได้หากมีเส้นทางของออยเลอร์

Example

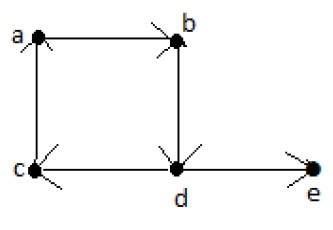
เส้นทางของออยเลอร์ = dcabde

ออยเลอร์เซอร์กิต

ในเส้นทางของออยเลอร์ถ้าจุดยอดเริ่มต้นเหมือนกับจุดยอดสิ้นสุดจะเรียกว่าวงจรของออยเลอร์

Example

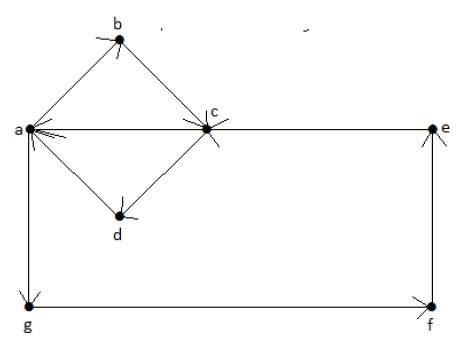
Euler’s Path = abcdagfeca

ทฤษฎีบทวงจรของออยเลอร์

กราฟที่เชื่อมต่อ 'G' สามารถข้ามผ่านได้ก็ต่อเมื่อจำนวนจุดยอดที่มีองศาคี่ใน G เป็น 2 หรือ 0 เท่านั้นกราฟที่เชื่อมต่อ G สามารถมีเส้นทางของออยเลอร์ได้ แต่ไม่ใช่วงจรของออยเลอร์หากมีจุดยอดสองจุดที่มี ปริญญาแปลก ๆ

Note - เส้นทางออยเลอร์นี้เริ่มต้นด้วยจุดยอดขององศาคี่และลงท้ายด้วยจุดยอดอื่น ๆ ของระดับคี่

Example

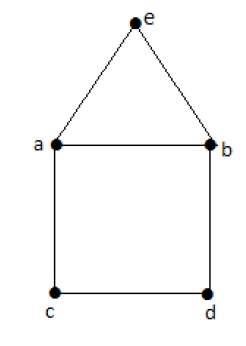
Euler’s Path- beabdca ไม่ใช่วงจรของออยเลอร์ แต่เป็นเส้นทางของออยเลอร์ เห็นได้ชัดว่ามันมีจุดยอด 2 องศาที่แปลก

Note - ในกราฟที่เชื่อมต่อ G ถ้าจำนวนจุดยอดที่มีองศาคี่ = 0 แสดงว่ามีวงจรของออยเลอร์อยู่

กราฟแฮมิลตัน

กราฟที่เชื่อมต่อ G ถูกกล่าวว่าเป็นกราฟแฮมิลตันหากมีวัฏจักรซึ่งมีจุดยอดทั้งหมดของ G

ทุกรอบเป็นวงจร แต่วงจรอาจมีหลายรอบ วงจรดังกล่าวเรียกว่าHamiltonian cycle ของ G.

เส้นทางแฮมิลตัน

กราฟที่เชื่อมต่อถูกกล่าวว่าเป็นแฮมิลตันหากมีจุดยอดของ G แต่ละครั้ง เส้นทางดังกล่าวเรียกว่าHamiltonian path.

Example

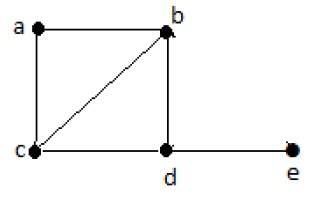
Hamiltonian Path- edbac.

Note

วงจรของออยเลอร์ประกอบด้วยขอบกราฟแต่ละด้านเพียงครั้งเดียว
ในวัฏจักรของแฮมิลตันสามารถข้ามขอบบางส่วนของกราฟได้

Example

ดูกราฟต่อไปนี้ -

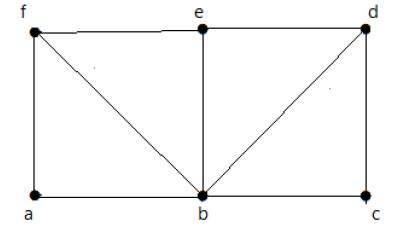
สำหรับกราฟที่แสดงด้านบน -

มีเส้นทางออยเลอร์ - เท็จ
วงจรออยเลอร์มีอยู่ - เท็จ
วัฏจักรของแฮมิลตันมีอยู่จริง - จริง
เส้นทางแฮมิลตันมีอยู่จริง - จริง

G มีจุดยอดสี่จุดที่มีองศาคี่ดังนั้นจึงไม่สามารถข้ามผ่านได้ เมื่อข้ามขอบภายในกราฟจะมีวัฏจักรแฮมิลตันผ่านจุดยอดทั้งหมด

ในบทนี้เราจะกล่าวถึงตัวอย่างมาตรฐานบางส่วนเพื่อแสดงให้เห็นถึงแนวคิดที่เราได้กล่าวไปแล้วในบทก่อนหน้านี้

ตัวอย่าง 1

Find the number of spanning trees in the following graph.

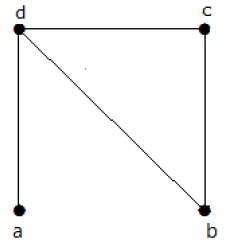
วิธีการแก้

จำนวนต้นไม้ที่ทอดที่ได้จากกราฟด้านบนคือ 3 ดังต่อไปนี้ -

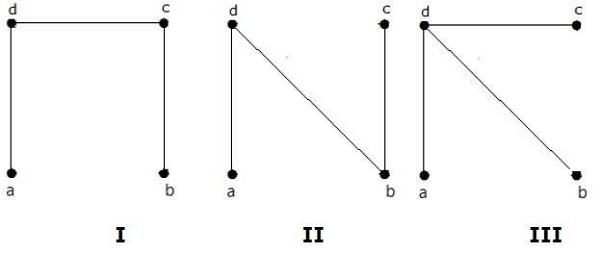
ทั้งสามนี้เป็นต้นไม้ที่ทอดสำหรับกราฟที่กำหนด ที่นี่กราฟ I และ II เป็นไอโซมอร์ฟิกซึ่งกันและกัน เห็นได้ชัดว่าจำนวนต้นไม้ที่ทอดไม่เป็นไอโซมอร์ฟิกคือสอง

ตัวอย่าง 2

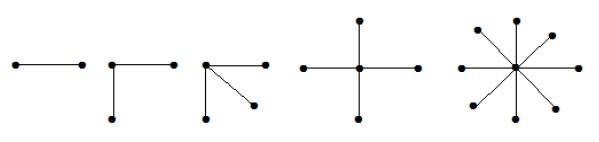
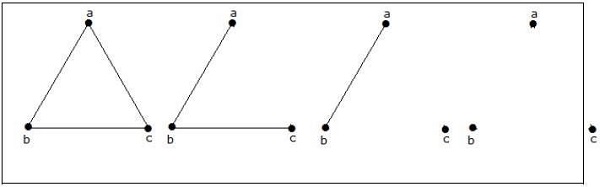
How many simple non-isomorphic graphs are possible with 3 vertices?

วิธีการแก้

มีกราฟที่ไม่ใช่ไอโซมอร์ฟิก 4 กราฟที่เป็นไปได้โดยมีจุดยอด 3 จุด แสดงไว้ด้านล่าง

ตัวอย่างที่ 3

Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.

วิธีการแก้

โดยผลรวมของทฤษฎีบทองศา

20 Σผม = 1 องศา (Vi) = 2 | E |

20 (3) = 2 | E |

| E | = 30

ตามสูตรของออยเลอร์

| V | + | R | = | E | + 2

20+ | R | = 30 + 2

| R | = 12

ดังนั้นจำนวนภูมิภาคคือ 12

ตัวอย่างที่ 4

What is the chromatic number of complete graph K_n?

วิธีการแก้

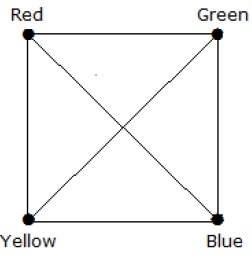
ในกราฟที่สมบูรณ์จุดยอดแต่ละจุดอยู่ติดกับจุดยอดที่เหลืออยู่ (n – 1) ดังนั้นจุดยอดแต่ละจุดจึงต้องใช้สีใหม่ ดังนั้นจำนวนสี K _n = n

ตัวอย่างที่ 5

What is the matching number for the following graph?

วิธีการแก้

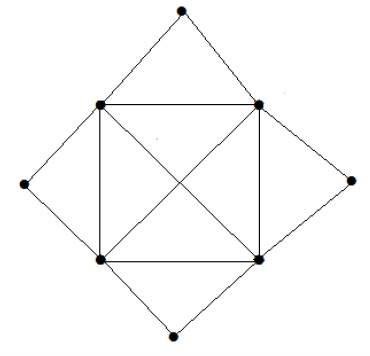
จำนวนจุดยอด = 9

เราจับคู่จุดยอดได้ 8 จุดเท่านั้น

หมายเลขที่ตรงกันคือ 4

ตัวอย่างที่ 6

What is the line covering number of for the following graph?

วิธีการแก้

จำนวนจุดยอด = | V | = n = 7

หมายเลขครอบคลุมบรรทัด = (α ₁ ) ≥ [n / 2] = 3

α ₁ ≥ 3

ด้วยการใช้ 3 ขอบเราสามารถครอบคลุมจุดยอดทั้งหมด

ดังนั้นบรรทัดที่ครอบคลุมหมายเลขคือ 3