ทฤษฎีกราฟ - Isomorphism

กราฟสามารถมีอยู่ในรูปแบบต่างๆโดยมีจำนวนจุดยอดขอบและการเชื่อมต่อขอบเดียวกัน กราฟดังกล่าวเรียกว่ากราฟไอโซมอร์ฟิก โปรดทราบว่าเราติดป้ายกำกับกราฟในบทนี้เป็นหลักเพื่อจุดประสงค์ในการอ้างอิงถึงและรับรู้จากกันและกัน

กราฟ Isomorphic

กราฟสองกราฟ G ₁และ G ₂ถูกกล่าวว่าเป็นไอโซมอร์ฟิกถ้า -

• จำนวนส่วนประกอบ (จุดยอดและขอบ) เหมือนกัน

• การเชื่อมต่อแบบ edge จะยังคงอยู่

Note- กล่าวโดยย่อจากกราฟไอโซมอร์ฟิกสองกราฟอันหนึ่งเป็นกราฟที่ปรับแต่งแล้วของอีกกราฟ กราฟที่ไม่มีป้ายกำกับสามารถคิดได้ว่าเป็นกราฟไอโซมอร์ฟิก

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

ถ้า G ₁ ≡ G ₂แล้ว -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

ลำดับองศาของ G ₁และ G ₂เหมือนกัน

ถ้าจุดยอด {V ₁ , V ₂ , .. Vk} เป็นวัฏจักรของความยาว K ใน G ₁ดังนั้นจุดยอด {f (V ₁ ), f (V ₂ ), … f (Vk)} ควรเป็นวัฏจักร ความยาว K จี2

เงื่อนไขทั้งหมดข้างต้นจำเป็นสำหรับกราฟ G ₁และ G ₂เป็นไอโซมอร์ฟิก แต่ไม่เพียงพอที่จะพิสูจน์ว่ากราฟนั้นเป็นไอโซมอร์ฟิก

• (G ₁ ≡ G ₂ ) ถ้าและเฉพาะในกรณีที่ (G ₁ - ₂ G ₂ -) โดยที่ G ₁และ G ₂เป็นกราฟธรรมดา

• (G ₁ ≡ G ₂ ) ถ้าเมทริกซ์ adjacency ของ G ₁และ G ₂เหมือนกัน

• (G ₁ ≡ G ₂ ) ในกรณีที่กราฟย่อยที่เกี่ยวข้องของ G ₁และ G _{2 เท่านั้น} (ได้จากการลบจุดยอดบางจุดใน G1 และรูปภาพในกราฟ G ₂ ) เป็นไอโซมอร์ฟิก

Example

กราฟใดต่อไปนี้เป็นไอโซมอร์ฟิก

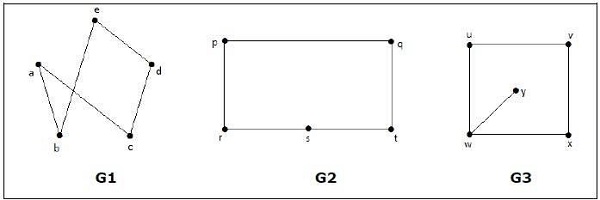
ในรูปแบบของกราฟ G ₃ , จุดสุดยอด 'w' มีเพียงระดับ 3 ในขณะที่ทุกจุดกราฟอื่น ๆ ที่มีการศึกษาระดับปริญญา 2. ดังนั้น G3 ไม่ isomorphic ถึง G ₁หรือ G 2

การเติมเต็ม G ₁และ G ₂คุณมี -

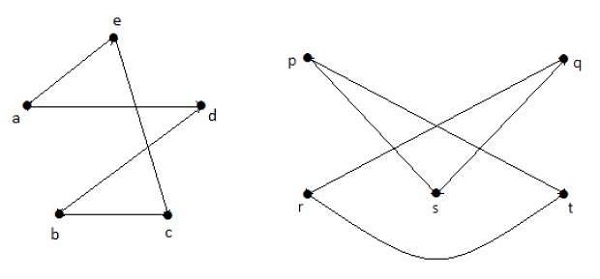
ที่นี่ (G ₁ - ≡ G ₂ -) ดังนั้น (G ₁ ≡ G ₂ )

กราฟระนาบ

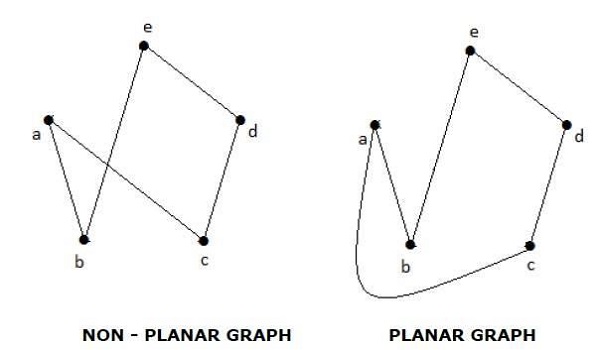
กราฟ 'G' จะถูกกล่าวว่าเป็นระนาบหากสามารถวาดบนระนาบหรือทรงกลมเพื่อไม่ให้ขอบทั้งสองตัดกันที่จุดที่ไม่ใช่จุดยอด

Example

ภูมิภาค

กราฟระนาบทุกเส้นแบ่งระนาบออกเป็นบริเวณที่เชื่อมต่อกันเรียกว่าพื้นที่

Example

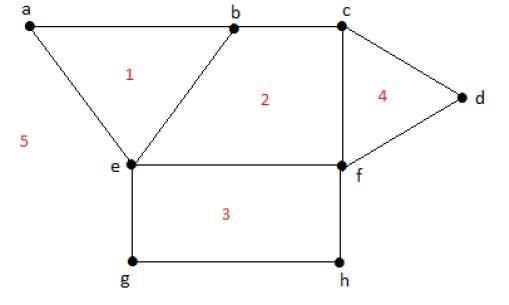
ระดับของภูมิภาคที่มีขอบเขต r = deg(r) = จำนวนขอบที่ล้อมรอบพื้นที่ r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8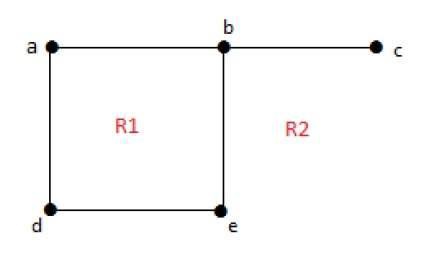

ระดับของภูมิภาคที่ไม่มีขอบเขต r = deg(r) = จำนวนขอบที่ล้อมรอบพื้นที่ r.

deg(R1) = 4
deg(R2) = 6

ในกราฟระนาบคุณสมบัติต่อไปนี้ถือเป็นสิ่งที่ดี -

ในกราฟระนาบที่มีจุดยอด 'n' ผลรวมขององศาของจุดยอดทั้งหมดคือ -

n Σ i = 1 องศา (V _i ) = 2 | E |

ตาม Sum of Degrees of Regions/ ทฤษฎีบทในกราฟระนาบที่มีพื้นที่ 'n' ผลรวมขององศาของพื้นที่คือ -

n Σ i = 1 องศา (ริ) = 2 | E |

จากทฤษฎีบทข้างต้นคุณสามารถสรุปได้ดังนี้ -

ในกราฟระนาบ

ถ้าองศาของแต่ละภูมิภาคคือ K ผลรวมขององศาของพื้นที่คือ -

K | R | = 2 | E |

หากระดับของแต่ละภูมิภาคมีค่าอย่างน้อย K (≥ K) ดังนั้น

K | R | ≤ 2 | E |

หากระดับของแต่ละภูมิภาคมีค่ามากที่สุด K (≤ K) ดังนั้น

K | R | ≥ 2 | E |

Note - สมมติว่าทุกภูมิภาคมีระดับเดียวกัน

ตาม Euler’s Formulae บนกราฟระนาบ

หากกราฟ 'G' เป็นระนาบที่เชื่อมต่อกันแล้ว

| V | + | R | = | E | + 2

ถ้ากราฟระนาบที่มีส่วนประกอบ 'K' แล้ว

| V | + | R | = | E | + (K + 1)

ที่ไหน, | V | คือจำนวนจุดยอด | E | คือจำนวนขอบและ | R | คือจำนวนภูมิภาค

Edge Vertex Inequality

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อโดยมีระดับของแต่ละภูมิภาคอย่างน้อย 'K'

| E | ≤ k / (k-2) {| v | - 2}

รู้ไหม | V | + | R | = | E | + 2

พ. | ร | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อแบบธรรมดาดังนั้น

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

มีจุดยอด V •∈ G อย่างน้อยหนึ่งจุดซึ่ง deg (V) ≤ 5

ถ้า 'G' เป็นกราฟระนาบที่เชื่อมต่อกันอย่างง่าย (มีขอบอย่างน้อย 2 ขอบ) และไม่มีสามเหลี่ยม

|E| ≤ {2|V| – 4}

ทฤษฎีบทของ Kuratowski

กราฟ 'G' ไม่เป็นระนาบเดียวและถ้าหาก 'G' มี subgraph ซึ่งเป็นมอร์ฟิคที่จะเค₅หรือ K 3,3

Homomorphism

กราฟสองกราฟ G ₁และ G ₂ถูกกล่าวว่าเป็นโฮโมมอร์ฟิกหากแต่ละกราฟเหล่านี้สามารถหาได้จากกราฟ 'G' เดียวกันโดยการหารขอบบางส่วนของ G ด้วยจุดยอดที่มากกว่า ดูตัวอย่างต่อไปนี้ -

แบ่งขอบ 'rs' ออกเป็นสองขอบโดยเพิ่มจุดยอดหนึ่งจุด

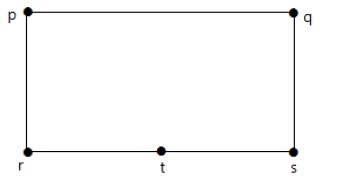
กราฟที่แสดงด้านล่างเป็นโฮโมมอร์ฟิกกับกราฟแรก

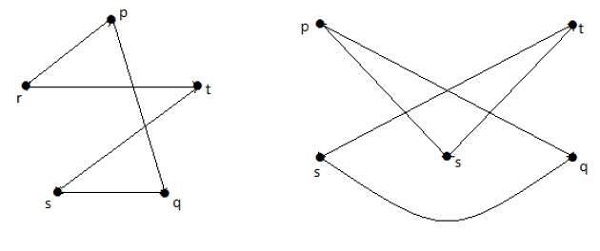
ถ้า G ₁เป็น isomorphic ถึง G ₂ดังนั้น G จะเป็น homeomorphic ถึง G2 แต่การสนทนาไม่จำเป็นต้องเป็นจริง

• กราฟใด ๆ ที่มีจุดยอด 4 จุดหรือน้อยกว่าจะเป็นแนวระนาบ

• กราฟใด ๆ ที่มีขอบ 8 หรือน้อยกว่าจะเป็นแนวระนาบ

• กราฟสมบูรณ์ K _nคือระนาบถ้า n ≤ 4 เท่านั้น

• กราฟสองส่วนที่สมบูรณ์ K _{m, n}เป็นระนาบถ้า m ≤ 2 หรือ n ≤ 2 เท่านั้น

• กราฟไม่ใช่ภาพถ่ายที่เรียบง่ายด้วยจำนวนขั้นต่ำของจุดมีความสมบูรณ์แบบของกราฟ K 5

• กราฟง่ายไม่ใช่ภาพถ่ายที่มีจำนวนขั้นต่ำของขอบเป็น K _3, 3

กราฟหลายเหลี่ยม

กราฟระนาบที่เชื่อมต่ออย่างง่ายเรียกว่ากราฟรูปหลายเหลี่ยมหากระดับของจุดยอดแต่ละจุดมีค่า≥ 3 นั่นคือ deg (V) ≥ 3 ∀ V ∈ G

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |