ทฤษฎีกราฟ - ความสามารถในการย้อนกลับ

กราฟสามารถข้ามผ่านได้หากคุณสามารถวาดเส้นทางระหว่างจุดยอดทั้งหมดโดยไม่ต้องย้อนเส้นทางเดิม ตามเส้นทางนี้มีบางประเภทเช่นเส้นทางของออยเลอร์และวงจรของออยเลอร์ซึ่งอธิบายไว้ในบทนี้

เส้นทางของออยเลอร์

เส้นทางของออยเลอร์มีขอบแต่ละด้านของ 'G' หนึ่งครั้งและแต่ละจุดยอดของ 'G' อย่างน้อยหนึ่งครั้ง กราฟที่เชื่อมต่อ G ถูกกล่าวว่าสามารถข้ามผ่านได้หากมีเส้นทางของออยเลอร์

Example

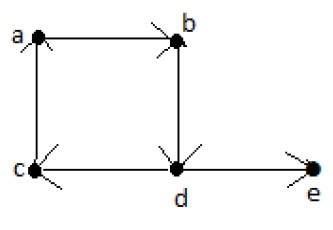
เส้นทางของออยเลอร์ = dcabde

ออยเลอร์เซอร์กิต

ในเส้นทางของออยเลอร์ถ้าจุดยอดเริ่มต้นเหมือนกับจุดยอดสิ้นสุดจะเรียกว่าวงจรของออยเลอร์

Example

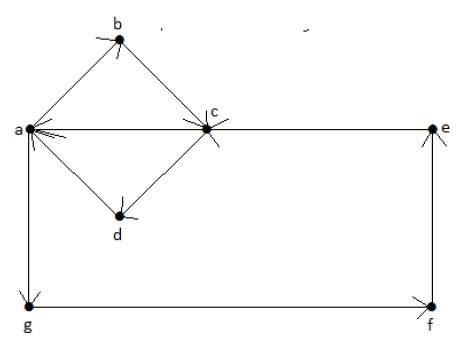
Euler’s Path = abcdagfeca

ทฤษฎีบทวงจรของออยเลอร์

กราฟที่เชื่อมต่อ 'G' สามารถข้ามผ่านได้ก็ต่อเมื่อจำนวนจุดยอดที่มีองศาคี่ใน G เป็น 2 หรือ 0 เท่านั้นกราฟที่เชื่อมต่อ G สามารถมีเส้นทางของออยเลอร์ได้ แต่ไม่ใช่วงจรของออยเลอร์หากมีจุดยอดสองจุดที่มี องศาแปลก ๆ

Note - เส้นทางออยเลอร์นี้เริ่มต้นด้วยจุดยอดขององศาคี่และลงท้ายด้วยจุดยอดอื่น ๆ ของระดับคี่

Example

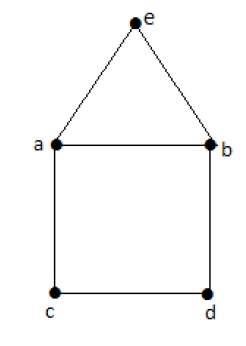
Euler’s Path- beabdca ไม่ใช่วงจรของออยเลอร์ แต่เป็นเส้นทางของออยเลอร์ เห็นได้ชัดว่ามันมีจุดยอด 2 องศาที่แปลก

Note - ในกราฟที่เชื่อมต่อ G ถ้าจำนวนจุดยอดที่มีองศาคี่ = 0 แสดงว่ามีวงจรของออยเลอร์อยู่

กราฟแฮมิลตัน

กราฟที่เชื่อมต่อ G ถูกกล่าวว่าเป็นกราฟแฮมิลตันหากมีวัฏจักรซึ่งมีจุดยอดทั้งหมดของ G

ทุกรอบเป็นวงจร แต่วงจรอาจมีหลายรอบ วงจรดังกล่าวเรียกว่าHamiltonian cycle ของ G.

เส้นทางแฮมิลตัน

กราฟที่เชื่อมต่อจะถูกกล่าวว่าเป็นแฮมิลตันหากมีจุดยอดของ G แต่ละจุดเพียงครั้งเดียว เส้นทางดังกล่าวเรียกว่าHamiltonian path.

Example

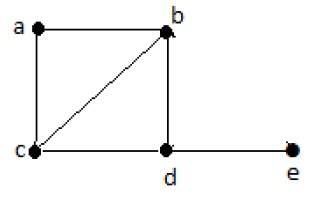
Hamiltonian Path- edbac.

Note

• วงจรของออยเลอร์ประกอบด้วยขอบกราฟแต่ละด้านเพียงครั้งเดียว

• ในวัฏจักรแฮมิลตันสามารถข้ามขอบบางส่วนของกราฟได้

Example

ดูกราฟต่อไปนี้ -

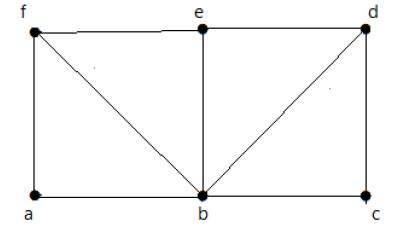
สำหรับกราฟที่แสดงด้านบน -

• มีเส้นทางออยเลอร์ - เท็จ

• วงจรออยเลอร์มีอยู่ - เท็จ

• วัฏจักรของแฮมิลตันมีอยู่จริง - จริง

• เส้นทางแฮมิลตันมีอยู่จริง - จริง

G มีจุดยอดสี่จุดที่มีองศาคี่ดังนั้นจึงไม่สามารถข้ามผ่านได้ เมื่อข้ามขอบภายในกราฟจะมีวัฏจักรแฮมิลตันผ่านจุดยอดทั้งหมด