ทฤษฎีกราฟ - การเชื่อมต่อ

การสำรวจกราฟจากจุดยอดหนึ่งไปยังอีกจุดหนึ่งเป็นไปได้หรือไม่นั้นขึ้นอยู่กับการเชื่อมต่อของกราฟ การเชื่อมต่อเป็นแนวคิดพื้นฐานในทฤษฎีกราฟ การเชื่อมต่อกำหนดว่ากราฟเชื่อมต่อหรือไม่ได้เชื่อมต่อ มีหัวข้อย่อยตามขอบและจุดยอดซึ่งเรียกว่าการเชื่อมต่อขอบและการเชื่อมต่อจุดสุดยอด ให้เราพูดคุยโดยละเอียด

การเชื่อมต่อ

กราฟบอกว่าเป็น connected if there is a path between every pair of vertex. จากจุดยอดทุกจุดไปยังจุดยอดอื่น ๆ ควรมีเส้นทางในการสำรวจ ที่เรียกว่าการเชื่อมต่อของกราฟ กราฟที่มีจุดยอดและขอบที่ขาดการเชื่อมต่อหลายจุดถูกตัดการเชื่อมต่อ

Example 1

ในกราฟต่อไปนี้เป็นไปได้ที่จะเดินทางจากจุดยอดหนึ่งไปยังจุดยอดอื่น ๆ ตัวอย่างเช่นเราสามารถข้ามจากจุดยอด 'a' ไปยังจุดยอด 'e' โดยใช้เส้นทาง 'ab-e'

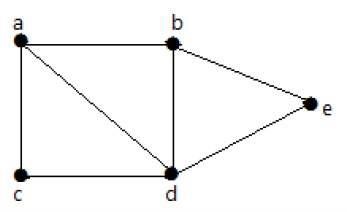
Example 2

ในตัวอย่างต่อไปนี้การข้ามจากจุดยอด 'a' ไปยังจุดยอด 'f' เป็นไปไม่ได้เนื่องจากไม่มีเส้นทางระหว่างทั้งสองโดยตรงหรือโดยอ้อม ดังนั้นจึงเป็นกราฟที่ไม่มีการเชื่อมต่อ

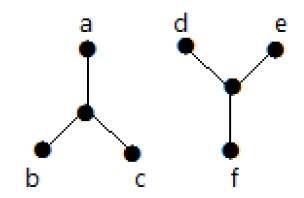
ตัด Vertex

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จุดยอด V ∈ G เรียกว่าจุดยอดตัดของ 'G' ถ้า 'G-V' (ลบ 'V' จาก 'G') ส่งผลให้กราฟขาดการเชื่อมต่อ การลบจุดยอดตัดออกจากกราฟจะแบ่งออกเป็นกราฟสองกราฟขึ้นไป

Note - การลบจุดยอดที่ถูกตัดออกอาจทำให้กราฟขาดการเชื่อมต่อ

กราฟที่เชื่อมต่อ 'G' อาจมีจุดยอดตัดได้มากที่สุด (n – 2)

Example

ในกราฟต่อไปนี้จุดยอด 'e' และ 'c' คือจุดยอดตัด

เมื่อลบ 'e' หรือ 'c' ออกกราฟจะกลายเป็นกราฟที่ไม่เชื่อมต่อ

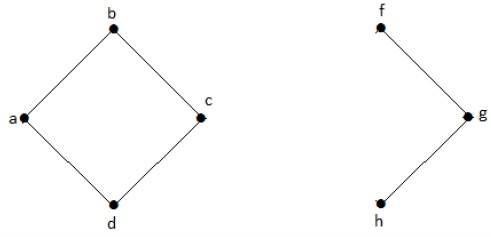
หากไม่มี 'g' จะไม่มีเส้นทางระหว่างจุดยอด 'c' และจุดยอด 'h' และอื่น ๆ อีกมากมาย ดังนั้นจึงเป็นกราฟที่ตัดการเชื่อมต่อโดยมีจุดยอดตัดเป็น 'e' ในทำนองเดียวกัน 'c' ยังเป็นจุดยอดตัดสำหรับกราฟด้านบน

ตัดขอบ (สะพาน)

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน ขอบ 'e' ∈ G เรียกว่าคมตัดถ้า 'G-e' ส่งผลให้กราฟขาดการเชื่อมต่อ

หากการลบขอบออกจากกราฟจะทำให้เกิดกราฟสองกราฟขึ้นไปขอบนั้นจะเรียกว่า Cut Edge

Example

ในกราฟต่อไปนี้ขอบตัดคือ [(c, e)]

การลบขอบ (c, e) ออกจากกราฟจะกลายเป็นกราฟที่ขาดการเชื่อมต่อ

ในกราฟด้านบนการลบขอบ (c, e) จะแบ่งกราฟออกเป็นสองส่วนซึ่งไม่ใช่กราฟที่ไม่มีการเชื่อมต่อ ดังนั้นขอบ (c, e) จึงเป็นขอบตัดของกราฟ

Note - ให้ 'G' เป็นกราฟที่เชื่อมต่อกับจุดยอด 'n' แล้ว

• ขอบตัด e ∈ G ถ้าขอบ 'e' ไม่ได้เป็นส่วนหนึ่งของรอบใด ๆ ใน G

• จำนวนคมตัดสูงสุดที่ทำได้คือ 'n-1'

• เมื่อใดก็ตามที่มีขอบตัดจะมีจุดยอดตัดด้วยเนื่องจากจุดยอดของขอบตัดอย่างน้อยหนึ่งจุดเป็นจุดยอดตัด

• หากมีจุดยอดตัดอยู่อาจมีหรือไม่มีคมตัดก็ได้

ตัดชุดกราฟ

ให้ 'G' = (V, E) เป็นกราฟที่เชื่อมต่อ ชุดย่อย E ของ E เรียกว่าชุดตัดของ G หากการลบขอบทั้งหมดของ E 'ออกจาก G ทำให้ G ตัดการเชื่อมต่อ

หากการลบขอบจำนวนหนึ่งออกจากกราฟทำให้ขาดการเชื่อมต่อขอบที่ถูกลบเหล่านั้นจะเรียกว่าชุดตัดของกราฟ

Example

ดูกราฟต่อไปนี้ ชุดตัดคือ E1 = {e1, e3, e5, e8}

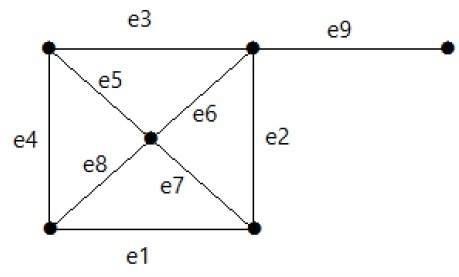
หลังจากลบชุดตัด E1 ออกจากกราฟแล้วจะปรากฏดังนี้ -

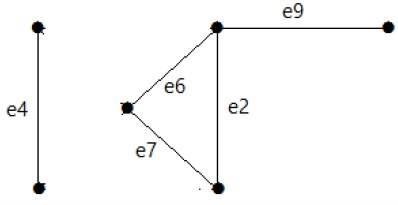
ในทำนองเดียวกันมีชุดตัดอื่น ๆ ที่สามารถตัดการเชื่อมต่อของกราฟได้ -

• E3 = {e9} - ชุดตัดที่เล็กที่สุดของกราฟ

• E4 = {e3, e4, e5}

การเชื่อมต่อ Edge

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จำนวนขอบขั้นต่ำที่การลบทำให้ตัดการเชื่อมต่อ 'G' เรียกว่าการเชื่อมต่อขอบของ G

Notation - λ (G)

กล่าวอีกนัยหนึ่งคือ number of edges in a smallest cut set of G เรียกว่าการเชื่อมต่อขอบของ G.

ถ้า 'G' มีคมตัดแล้วλ (G) คือ 1 (การเชื่อมต่อขอบของ G)

Example

ดูกราฟต่อไปนี้ การลบขอบขั้นต่ำสองเส้นออกทำให้กราฟที่เชื่อมต่อขาดการเชื่อมต่อ ดังนั้นการเชื่อมต่อแบบ edge (λ (G)) คือ 2

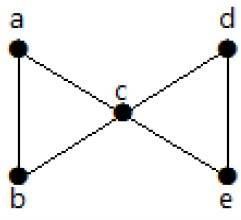
ต่อไปนี้เป็นสี่วิธีในการตัดการเชื่อมต่อของกราฟโดยการลบสองขอบ -

การเชื่อมต่อ Vertex

ให้ 'G' เป็นกราฟที่เชื่อมต่อกัน จำนวนจุดต่ำสุดที่การลบทำให้ 'G' ถูกตัดการเชื่อมต่อหรือลด 'G' ในกราฟเล็กน้อยเรียกว่าการเชื่อมต่อจุดยอด

Notation - เค (G)

Example

ในกราฟด้านบนการลบจุดยอด 'e' และ 'i' ทำให้กราฟถูกตัดการเชื่อมต่อ

ถ้า G มีจุดยอดตัดแล้ว K (G) = 1

Notation - สำหรับกราฟ G ที่เชื่อมต่อใด ๆ

K (G) ≤λ (G) ≤δ (G)

การเชื่อมต่อ Vertex (K (G)), การเชื่อมต่อที่ขอบ (λ (G)), จำนวนองศาขั้นต่ำของ G (δ (G))

Example

คำนวณλ (G) และ K (G) สำหรับกราฟต่อไปนี้ -

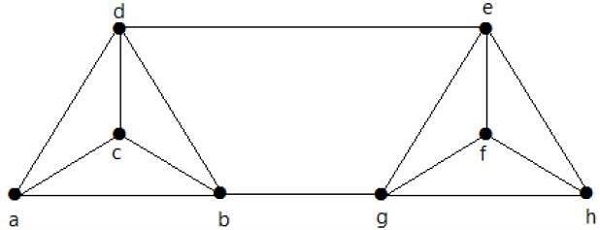
Solution

จากกราฟ

δ (G) = 3

K (G) ≤λ (G) ≤δ (G) = 3 (1)

K (G) ≥ 2 (2)

การลบขอบ {d, e} และ {b, h} เราสามารถยกเลิกการเชื่อมต่อ G

ดังนั้น,

λ (G) = 2

2 ≤λ (G) ≤δ (G) = 2 (3)

จาก (2) และ (3) จุดยอดการเชื่อมต่อ K (G) = 2