วงจรเลขคณิต
ในบทที่แล้วเราได้กล่าวถึงการใช้งานพื้นฐานของ op-amp โปรดทราบว่าพวกมันอยู่ภายใต้การดำเนินการเชิงเส้นของ op-amp ในบทนี้ให้เราพูดคุยเกี่ยวกับวงจรเลขคณิตซึ่งเป็นแอปพลิเคชันเชิงเส้นของ op-amp
วงจรอิเล็กทรอนิกส์ซึ่งทำหน้าที่ทางคณิตศาสตร์เรียกว่าเป็น arithmetic circuits. การใช้ออปแอมป์คุณสามารถสร้างวงจรเลขคณิตพื้นฐานเช่นไฟล์adder และก subtractor. ในบทนี้คุณจะได้เรียนรู้เกี่ยวกับแต่ละข้อโดยละเอียด
แอดเดอร์
แอดเดอร์เป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งเท่ากับผลรวมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงวงจรแอดเดอร์ที่ใช้ op-amp
adder ที่ใช้ op-amp จะสร้างเอาต์พุตที่เท่ากับผลรวมของแรงดันไฟฟ้าอินพุตที่ใช้ที่ขั้วต่อกลับด้าน จะเรียกว่าเป็นsumming amplifierเนื่องจากเอาต์พุตเป็นแบบขยาย
circuit diagram ของ adder ที่ใช้ op-amp แสดงในรูปต่อไปนี้ -
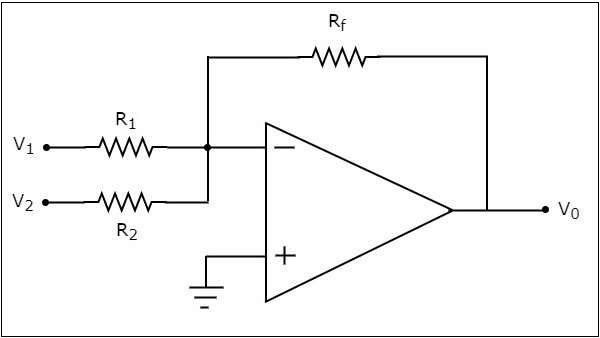
ในวงจรข้างต้นขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเชื่อมต่อกับกราวด์ นั่นหมายความว่าศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้าน
ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเหมือนกับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์
nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ
$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {R_f} = 0 $$
$$ => \ frac {V_1} {R_1} - \ frac {V_2} {R_2} = \ frac {V_0} {R_f} $$
$$ => V_ {0} = R_ {f} \ left (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ right) $$
ถ้า $ R_ {f} = R_ {1} = R_ {2} = R $ ดังนั้นแรงดันเอาต์พุต $ V_ {0} $ จะเป็น -
$$ V_ {0} = - R {} \ left (\ frac {V_1} {R} + \ frac {V_2} {R} \ right) $$
$$ => V_ {0} = - (V_ {1} + V_ {2}) $$
ดังนั้นวงจร adder แบบ op-amp ที่กล่าวถึงข้างต้นจะสร้างผลรวมของแรงดันไฟฟ้าอินพุตสองตัว $ v_ {1} $ และ $ v_ {1} $ เป็นเอาต์พุตเมื่อตัวต้านทานทั้งหมดที่มีอยู่ในวงจรมีค่าเท่ากัน . โปรดทราบว่าแรงดันเอาต์พุต $ V_ {0} $ ของวงจรแอดเดอร์จะมีnegative signซึ่งระบุว่ามีความแตกต่างของเฟส180 0ระหว่างอินพุตและเอาต์พุต
ตัวลบ
ตัวลบเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งเท่ากับผลต่างของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงวงจรตัวลบที่ใช้ op-amp
ตัวลบที่ใช้ op-amp จะสร้างเอาต์พุตเท่ากับความแตกต่างของแรงดันไฟฟ้าอินพุตที่ใช้ที่ขั้วต่อกลับด้านและไม่กลับด้าน จะเรียกว่าเป็นdifference amplifierเนื่องจากเอาต์พุตเป็นแบบขยาย
circuit diagram ของตัวลบตาม op-amp แสดงในรูปต่อไปนี้ -
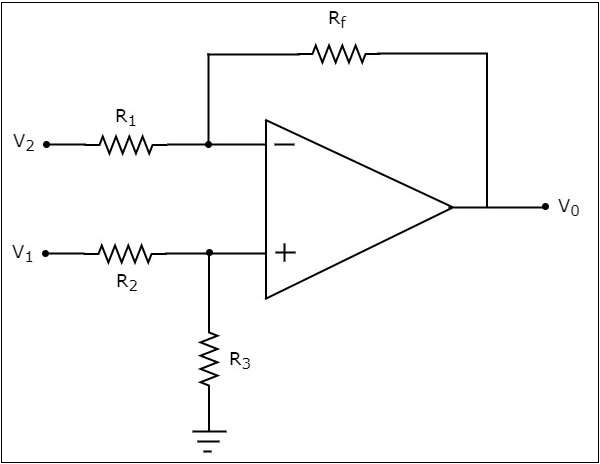
ตอนนี้ให้เราหานิพจน์สำหรับแรงดันไฟฟ้าขาออก $ V_ {0} $ ของวงจรข้างต้นโดยใช้ superposition theorem โดยใช้ขั้นตอนต่อไปนี้ -
ขั้นตอนที่ 1
ประการแรกให้เราคำนวณแรงดันขาออก $ V_ {01} $ โดยพิจารณาเฉพาะ $ V_ {1} $
สำหรับสิ่งนี้ให้กำจัด $ V_ {2} $ โดยทำให้ไฟฟ้าลัดวงจร จากนั้นเราจะได้รับmodified circuit diagram ดังแสดงในรูปต่อไปนี้ -

ตอนนี้ใช้ไฟล์ voltage division principleคำนวณแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp
$$ => V_ {p} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) $$
ตอนนี้วงจรด้านบนดูเหมือนแอมพลิฟายเออร์ที่ไม่กลับด้านที่มีแรงดันไฟฟ้าอินพุต $ V_ {p} $ ดังนั้นแรงดันเอาต์พุต $ V_ {01} $ ของวงจรข้างต้นจะเป็น
$$ V_ {01} = V_ {p} \ left (1+ \ frac {R_f} {R_1} \ right) $$
แทนค่าของ $ V_ {p} $ ในสมการข้างต้นเราได้แรงดันเอาต์พุต $ V_ {01} $ โดยพิจารณาเฉพาะ $ V_ {1} $ เป็น -
$$ V_ {01} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) $$
ขั้นตอนที่ 2
ในขั้นตอนนี้ให้เราหาค่าแรงดันเอาต์พุต $ V_ {02} $ โดยพิจารณาเฉพาะ $ V_ {2} $ เช่นเดียวกับในขั้นตอนข้างต้นกำจัด $ V_ {1} $ โดยทำให้ไฟฟ้าลัดวงจร modified circuit diagram แสดงดังรูปต่อไปนี้

คุณสามารถสังเกตได้ว่าแรงดันไฟฟ้าที่ขั้วอินพุตแบบไม่กลับด้านของ op-amp จะเป็นศูนย์โวลต์ หมายความว่าวงจรข้างต้นเป็นเพียงinverting op-amp. ดังนั้นแรงดันเอาต์พุต $ V_ {02} $ ของวงจรข้างต้นจะเป็น -
$$ V_ {02} = \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
ขั้นตอนที่ 3
ในขั้นตอนนี้เราจะได้รับแรงดันเอาต์พุต $ V_ {0} $ ของวงจรตัวลบโดย adding the output voltagesได้รับในขั้นตอนที่ 1 และขั้นตอนที่ 2 ในทางคณิตศาสตร์สามารถเขียนเป็น
$$ V_ {0} = V_ {01} + V_ {02} $$
แทนที่ค่าของ $ V_ {01} $ และ $ V_ {02} $ ในสมการข้างบนเราจะได้ -
$$ V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) + \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) - \ left (\ frac {R_f} {R_1} \ right) V_ {2} $$
ถ้า $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $ ดังนั้นแรงดันเอาต์พุต $ V_ {0} $ จะเป็น
$$ V_ {0} = V_ {1} \ left (\ frac {R} {R + R} \ right) \ left (1+ \ frac {R} {R} \ right) - \ left (\ frac { R} {R} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ left (\ frac {R} {2R} \ right) (2) - (1) V_ {2} $$
$$ V_ {0} = V_ {1} -V_ {2} $$
ดังนั้นวงจรตัวลบที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นความแตกต่างของแรงดันไฟฟ้าอินพุตสองตัว $ V_ {1} $ และ $ V_ {2} $ เมื่อตัวต้านทานทั้งหมดที่มีอยู่ในวงจรมีค่าเท่ากัน .