Log และ Anti Log Amplifiers
วงจรอิเล็กทรอนิกส์ที่ดำเนินการทางคณิตศาสตร์เช่นลอการิทึมและต่อต้านลอการิทึม (เลขชี้กำลัง) ที่มีการขยายสัญญาณเรียกว่า Logarithmic amplifier และ Anti-Logarithmic amplifier ตามลำดับ
ในบทนี้จะกล่าวถึงไฟล์ Logarithmic amplifier และ Anti-Logarithmic amplifierในรายละเอียด. โปรดทราบว่าเครื่องขยายเสียงเหล่านี้อยู่ภายใต้การใช้งานที่ไม่ใช่เชิงเส้น
เครื่องขยายเสียงลอการิทึม
ก logarithmic amplifierหรือก log amplifierเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตที่เป็นสัดส่วนกับลอการิทึมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับแอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp
แอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp จะสร้างแรงดันไฟฟ้าที่เอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมของแรงดันไฟฟ้าที่ใช้กับตัวต้านทานที่เชื่อมต่อกับขั้วกลับด้าน circuit diagram ของแอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -
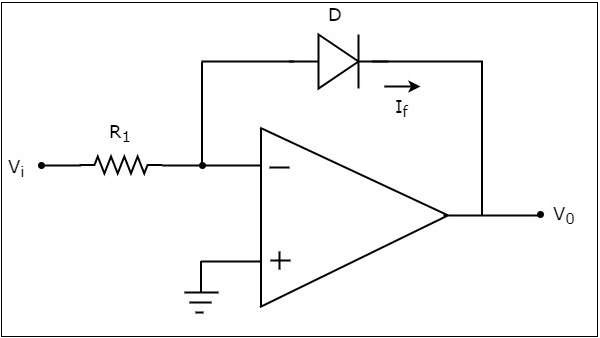
ในวงจรข้างต้นขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเชื่อมต่อกับกราวด์ นั่นหมายถึงศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp
ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของออปแอมป์จะเท่ากับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านจะเป็นศูนย์โวลต์
nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ -
$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$
$$ => I_ {f} = \ frac {V_i} {R_1} ...... สมการ 1 $$
ต่อไปนี้คือไฟล์ equation for current ไหลผ่านไดโอดเมื่ออยู่ในอคติไปข้างหน้า -
$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... สมการ 2 $$
ที่ไหน
$ I_ {s} $ คือกระแสอิ่มตัวของไดโอด
$ V_ {f} $ คือแรงดันตกคร่อมไดโอดเมื่อมันอยู่ในไบแอสไปข้างหน้า
$ V_ {T} $ คือแรงดันไฟฟ้าเทียบเท่าความร้อนของไดโอด
KVL equation รอบ ๆ ข้อเสนอแนะของ op amp จะเป็น -
$$ 0-V_ {f} -V_ {0} = 0 $$
$$ => V_ {f} = - V_ {0} $$
การแทนที่ค่า $ V_ {f} $ ในสมการ 2 เราจะได้ -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} ...... สมการ 3 $$
สังเกตว่าเงื่อนไขด้านซ้ายมือของทั้งสมการ 1 และสมการ 3 เหมือนกัน ดังนั้นจึงถือสมการทางด้านขวามือของทั้งสองสมการดังที่แสดงด้านล่าง -
$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
การสมัคร natural logarithm ทั้งสองด้านเราได้รับ -
$$ ใน \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$
$$ V_ {0} = - {nV_T} ใน \ left (\ frac {V_i} {R_1I_s} \ right) $$
โปรดทราบว่าในสมการข้างต้นพารามิเตอร์ n, $ {V_T} $ และ $ I_ {s} $ เป็นค่าคงที่ ดังนั้นแรงดันเอาต์พุต $ V_ {0} $ จะเป็นสัดส่วนกับnatural logarithm ของแรงดันไฟฟ้าอินพุต $ V_ {i} $ สำหรับค่าความต้านทานคงที่ $ R_ {1} $
ดังนั้นวงจรแอมพลิฟายเออร์ลอการิทึมแบบ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมธรรมชาติของแรงดันไฟฟ้าอินพุต $ {V_T} $ เมื่อ $ {R_1I_s} = 1V $
สังเกตว่าแรงดันเอาต์พุต $ V_ {0} $ มี negative signซึ่งระบุว่ามีความแตกต่างของเฟส180 0ระหว่างอินพุตและเอาต์พุต
แอมพลิฟายเออร์ต่อต้านลอการิทึม
อัน anti-logarithmic amplifierหรือ anti-log amplifierเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตที่เป็นสัดส่วนกับค่าต่อต้านลอการิทึมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp
แอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp จะสร้างแรงดันไฟฟ้าที่เอาต์พุตซึ่งเป็นสัดส่วนกับค่าต่อต้านลอการิทึมของแรงดันไฟฟ้าที่ใช้กับไดโอดที่เชื่อมต่อกับขั้วกลับด้าน
circuit diagram ของแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

ในวงจรที่แสดงด้านบนขั้วอินพุตที่ไม่กลับด้านของ op-amp เชื่อมต่อกับกราวด์ หมายความว่าศูนย์โวลต์ถูกนำไปใช้กับขั้วอินพุตที่ไม่กลับด้าน
ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุทกลับด้านของ op-amp จะเท่ากับแรงดันไฟฟ้าที่มีอยู่ที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านจะเป็นศูนย์โวลต์
nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ -
$$ - I_ {f} + \ frac {0-V_0} {R_f} = 0 $$
$$ => - \ frac {V_0} {R_f} = I_ {f} $$
$$ => V_ {0} = - R_ {f} I_ {f} ......... สมการ 4 $$
เรารู้ว่าสมการของกระแสที่ไหลผ่านไดโอดเมื่ออยู่ในรูปแบบไบแอสไปข้างหน้าเป็นดังที่ระบุไว้ด้านล่าง -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)} $$
แทนที่ค่าของ $ I_ {f} $ ในสมการ 4 เราจะได้
$$ V_ {0} = - R_ {f} \ left \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} \ right \} $$
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} ...... สมการ 5 $$
สมการ KVL ที่ด้านอินพุตของขั้วกลับด้านของ op amp จะเป็น
$$ V_ {i} -V_ {f} = 0 $$
$$ V_ {f} = V_ {i} $$
การแทนที่ค่าของสมการ 5 เราจะได้ -
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ right)}} $$
โปรดทราบว่าในสมการข้างต้นพารามิเตอร์ n $ {V_T} $ และ $ I_ {s} $ เป็นค่าคงที่ ดังนั้นแรงดันเอาต์พุต $ {V_0} $ จะเป็นสัดส่วนกับanti-natural logarithm (เลขชี้กำลัง) ของแรงดันไฟฟ้าอินพุต $ {V_i} $ สำหรับค่าคงที่ของความต้านทานป้อนกลับ $ {R_f} $
ดังนั้นวงจรแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมต่อต้านธรรมชาติ (เลขชี้กำลัง) ของแรงดันไฟฟ้าอินพุต $ {V_i} $ เมื่อ, $ {R_fI_s} = 1V $ สังเกตว่าแรงดันเอาต์พุต $ {V_0} $ กำลังมีnegative signซึ่งระบุว่ามีความแตกต่างของเฟส180 0ระหว่างอินพุตและเอาต์พุต