พื้นฐานของวงจรรวม

อัน electronic circuit คือกลุ่มของชิ้นส่วนอิเล็กทรอนิกส์ที่เชื่อมต่อเพื่อวัตถุประสงค์เฉพาะ

วงจรอิเล็กทรอนิกส์แบบธรรมดาสามารถออกแบบได้อย่างง่ายดายเนื่องจากต้องใช้ชิ้นส่วนอิเล็กทรอนิกส์และการเชื่อมต่อที่ไม่ต่อเนื่องเพียงไม่กี่ชิ้น อย่างไรก็ตามการออกแบบวงจรอิเล็กทรอนิกส์ที่ซับซ้อนเป็นเรื่องยากเนื่องจากต้องใช้ชิ้นส่วนอิเล็กทรอนิกส์แบบแยกส่วนและการเชื่อมต่อจำนวนมากขึ้น นอกจากนี้ยังต้องใช้เวลาในการสร้างวงจรที่ซับซ้อนและความน่าเชื่อถือก็น้อยลงด้วย ปัญหาเหล่านี้สามารถเอาชนะได้ด้วยวงจรรวม

วงจรรวม (IC)

หากชิ้นส่วนอิเล็กทรอนิกส์หลายชิ้นเชื่อมต่อกันบนชิปของวัสดุเซมิคอนดักเตอร์เพียงตัวเดียวชิปนั้นจะเรียกว่าเป็น Integrated Circuit (IC). ประกอบด้วยส่วนประกอบที่ใช้งานและแฝง

บทนี้จะกล่าวถึงข้อดีและประเภทของ IC

ข้อดีของวงจรรวม

วงจรรวมมีข้อดีหลายประการ พวกเขาจะกล่าวถึงด้านล่าง -

Compact size - สำหรับฟังก์ชันการทำงานที่กำหนดคุณสามารถรับวงจรที่มีขนาดเล็กกว่าโดยใช้ ICs เทียบกับวงจรที่สร้างขึ้นโดยใช้วงจรแยก
Lesser weight- วงจรที่สร้างด้วย IC มีน้ำหนักน้อยกว่าเมื่อเทียบกับน้ำหนักของวงจรแยกที่ใช้สำหรับการใช้ฟังก์ชันเดียวกันของ IC โดยใช้ IC เปรียบเทียบกับที่สร้างขึ้นโดยใช้วงจรแยก
Low power consumption - IC ใช้พลังงานต่ำกว่าวงจรแบบเดิมเนื่องจากมีขนาดและโครงสร้างที่เล็กกว่า
Reduced cost - IC มีให้ในราคาที่ถูกกว่าวงจรแยกเนื่องจากเทคโนโลยีการผลิตและการใช้วัสดุน้อยกว่าวงจรแยก
Increased reliability - เนื่องจากใช้การเชื่อมต่อน้อยกว่า IC จึงมีความน่าเชื่อถือเพิ่มขึ้นเมื่อเทียบกับวงจรดิจิทัล
Improved operating speeds - IC ทำงานด้วยความเร็วที่ดีขึ้นเนื่องจากความเร็วในการเปลี่ยนและใช้พลังงานน้อยลง

ประเภทของวงจรรวม

วงจรรวมมีสองประเภท − Analog Integrated Circuits and Digital Integrated Circuits.

วงจรรวมอนาล็อก

วงจรรวมที่ทำงานในช่วงค่าต่อเนื่องทั้งหมดของความกว้างของสัญญาณเรียกว่าเป็น Analog Integrated Circuits. สิ่งเหล่านี้แบ่งออกเป็นสองประเภทตามที่กล่าวไว้ที่นี่ -

Linear Integrated Circuits- IC แบบอะนาล็อกถูกกล่าวว่าเป็น Linear หากมีความสัมพันธ์เชิงเส้นระหว่างแรงดันและกระแส IC 741 ซึ่งเป็นออปแอมป์ 8-pin Dual In-line Package (DIP) เป็นตัวอย่างของ Linear IC
Radio Frequency Integrated Circuits- IC แบบอะนาล็อกถูกกล่าวว่าเป็น Non-Linear หากมีความสัมพันธ์แบบไม่เป็นเชิงเส้นระหว่างแรงดันและกระแส Non-Linear IC เรียกอีกอย่างว่า Radio Frequency IC

วงจรรวมดิจิตอล

หากวงจรรวมทำงานในระดับที่กำหนดไว้ล่วงหน้าเพียงไม่กี่ระดับแทนที่จะใช้งานสำหรับช่วงค่าต่อเนื่องทั้งหมดของแอมพลิจูดของสัญญาณเหล่านั้นจะเรียกว่า Digital Integrated Circuits.

ในบทต่อ ๆ ไปเราจะพูดถึงวงจรรวมเชิงเส้นต่างๆและการใช้งาน

Operational Amplifier หรือเรียกอีกอย่างว่า Op-Amp เป็นวงจรรวมซึ่งสามารถใช้เพื่อดำเนินการเชิงเส้นไม่ใช่เชิงเส้นและทางคณิตศาสตร์ต่างๆ op-amp คือไฟล์direct coupled high gain amplifier. คุณสามารถใช้งาน op-amp ได้ทั้งกับสัญญาณ AC และ DC บทนี้จะกล่าวถึงลักษณะและประเภทของออปแอมป์

การก่อสร้างเครื่องขยายเสียงในการทำงาน

ออปแอมป์ประกอบด้วยแอมพลิฟายเออร์ดิฟเฟอเรนเชียลตัวแปลระดับและเอาท์พุต แอมพลิฟายเออร์ดิฟเฟอเรนเชียลมีอยู่ในขั้นตอนอินพุตของ op-amp และด้วยเหตุนี้ op-amp จึงประกอบด้วยtwo input terminals. หนึ่งในเทอร์มินัลเหล่านั้นเรียกว่าinverting terminal และอีกอันเรียกว่า non-inverting terminal. เทอร์มินัลถูกตั้งชื่อตามความสัมพันธ์เฟสระหว่างอินพุตและเอาต์พุตตามลำดับ

ลักษณะของเครื่องขยายเสียงในการทำงาน

คุณสมบัติหรือพารามิเตอร์ที่สำคัญของแอมพลิฟายเออร์ที่ใช้งานได้มีดังนี้ -

การเพิ่มแรงดันไฟฟ้าของวงเปิด
แรงดันไฟฟ้าชดเชยเอาต์พุต
อัตราส่วนการปฏิเสธโหมดทั่วไป
อัตราการเคลื่อนที่

ส่วนนี้จะกล่าวถึงลักษณะเหล่านี้โดยละเอียดตามที่ระบุด้านล่าง -

การเพิ่มแรงดันไฟฟ้าของวงเปิด

การเพิ่มแรงดันไฟฟ้าแบบลูปเปิดของ op-amp คือค่าส่วนต่างที่เพิ่มขึ้นโดยไม่มีเส้นทางป้อนกลับใด ๆ

ในทางคณิตศาสตร์การเพิ่มแรงดันไฟฟ้าวงเปิดของ op-amp จะแสดงเป็น -

$$A_{v}= \frac{v_0}{v_1-v_2}$$

แรงดันไฟฟ้าชดเชยเอาต์พุต

แรงดันไฟฟ้าที่มีอยู่ที่เอาต์พุตของ op-amp เมื่อแรงดันไฟฟ้าขาเข้าที่แตกต่างกันเป็นศูนย์จะเรียกว่า as output offset voltage.

อัตราส่วนการปฏิเสธโหมดทั่วไป

อัตราส่วนการปฏิเสธโหมดทั่วไป (CMRR) ของ op-amp ถูกกำหนดให้เป็นอัตราส่วนของกำไรที่แตกต่างของวงปิด $A_{d}$ และโหมดทั่วไปที่ได้รับ $A_{c}$.

ในทางคณิตศาสตร์ CMRR สามารถแสดงเป็น -

$$CMRR=\frac{A_{d}}{A_{c}}$$

โปรดทราบว่าโหมดทั่วไปที่ได้รับ $A_{c}$ ของ op-amp คืออัตราส่วนของแรงดันเอาต์พุตโหมดทั่วไปและแรงดันไฟฟ้าอินพุตโหมดทั่วไป

อัตราการเคลื่อนที่

อัตราการหมุนของ op-amp หมายถึงอัตราสูงสุดของการเปลี่ยนแปลงของแรงดันไฟฟ้าขาออกเนื่องจากแรงดันไฟฟ้าขาเข้า

ในทางคณิตศาสตร์อัตราการฆ่า (SR) สามารถแสดงเป็น -

$$SR=Maximum\:of\:\frac{\text{d}V_{0}}{\text{d}t}$$

ที่ไหน $V_{0}$คือแรงดันไฟฟ้าขาออก โดยทั่วไปแล้วอัตราการฆ่าจะถูกวัดเป็นอย่างใดอย่างหนึ่ง$V/\mu\:Sec$ หรือ $V/m\:Sec$.

ประเภทของวงจรขยายการทำงาน

ออปแอมป์แสดงด้วยสัญลักษณ์สามเหลี่ยมที่มีสองอินพุตและหนึ่งเอาต์พุต

ออปแอมป์มีสองประเภท: Ideal Op-Amp และ Practical Op-Amp.

มีการกล่าวถึงในรายละเอียดตามที่ระบุด้านล่าง -

Op-Amp ในอุดมคติ

ออปแอมป์ในอุดมคติมีอยู่ในทางทฤษฎีเท่านั้นและไม่มีอยู่จริง equivalent circuit ของ op-amp ในอุดมคติจะแสดงในรูปด้านล่าง -

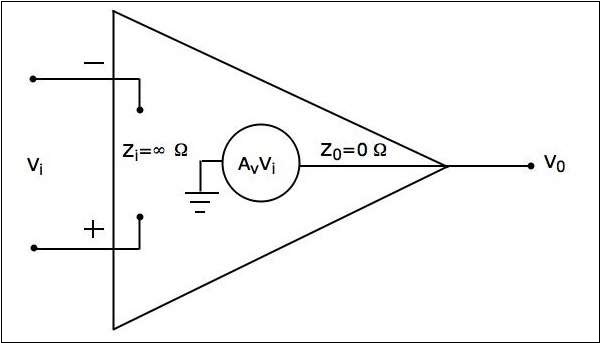
อัน ideal op-amp มีลักษณะดังต่อไปนี้ -

ความต้านทานของอินพุต $Z_{i}=\infty\Omega$
ความต้านทานขาออก $Z_{0}=0\Omega$
กำไรจากแรงดันไฟฟ้าวงเปิด $A_{v}=\infty$
ถ้า (ความแตกต่าง) แรงดันไฟฟ้าขาเข้า $V_{i}=0V$จากนั้นแรงดันขาออกจะเป็น $V_{0}=0V$
แบนด์วิดท์คือ infinity. หมายความว่า op-amp ในอุดมคติจะขยายสัญญาณของความถี่ใด ๆ โดยไม่มีการลดทอนใด ๆ
อัตราส่วนการปฏิเสธโหมดทั่วไป (CMRR) คือ infinity.
อัตราการเคลื่อนที่ (SR) คือ infinity. หมายความว่าออปแอมป์ในอุดมคติจะสร้างการเปลี่ยนแปลงของเอาต์พุตทันทีเพื่อตอบสนองต่อแรงดันไฟฟ้าขั้นตอนอินพุต

Op-Amp ที่ใช้งานได้จริง

ในทางปฏิบัติออปแอมป์ไม่เหมาะและเบี่ยงเบนไปจากลักษณะในอุดมคติเนื่องจากความไม่สมบูรณ์บางประการในระหว่างการผลิต equivalent circuit ของ op-amp ที่ใช้งานได้จริงแสดงในรูปต่อไปนี้ -

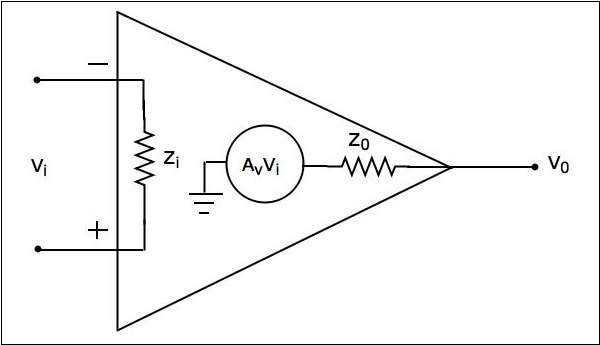
ก practical op-amp มีลักษณะดังต่อไปนี้ -

ความต้านทานของอินพุต $Z_{i}$ ตามลำดับ Mega ohms.
ความต้านทานขาออก $Z_{0}$ ตามลำดับ few ohms..
การเพิ่มแรงดันไฟฟ้าแบบวงเปิด, $A_{v}$ จะ high.

เมื่อคุณเลือก op-amp ที่ใช้งานได้จริงคุณควรตรวจสอบว่าเป็นไปตามเงื่อนไขต่อไปนี้หรือไม่ -

ความต้านทานของอินพุต $Z_{i}$ ควรสูงที่สุด
ความต้านทานขาออก $Z_{0}$ ควรต่ำที่สุด
การเพิ่มแรงดันไฟฟ้าแบบวงเปิด, $A_{v}$ ควรสูงที่สุด
แรงดันออฟเซ็ตเอาต์พุตควรต่ำที่สุด
แบนด์วิดท์ในการทำงานควรสูงที่สุด
CMRR ควรสูงที่สุด
อัตราการนอนหลับควรสูงที่สุด

Note - IC 741 op-amp เป็นออปแอมป์ยอดนิยมและใช้งานได้จริง

กล่าวกันว่าเป็นวงจร linearหากมีความสัมพันธ์เชิงเส้นระหว่างอินพุตและเอาต์พุต ในทำนองเดียวกันมีการกล่าวถึงวงจรnon-linearหากมีความสัมพันธ์ที่ไม่ใช่เชิงเส้นระหว่างอินพุตและเอาต์พุต

ออปแอมป์สามารถใช้ได้ทั้งในแอพพลิเคชั่นเชิงเส้นและไม่เชิงเส้น ต่อไปนี้เป็นแอปพลิเคชันพื้นฐานของ op-amp -

Inverting Amplifier
เครื่องขยายเสียงที่ไม่กลับด้าน
ผู้ติดตามแรงดันไฟฟ้า

บทนี้จะกล่าวถึงการใช้งานพื้นฐานเหล่านี้โดยละเอียด

Inverting Amplifier

แอมพลิฟายเออร์แบบกลับด้านจะรับอินพุตผ่านเทอร์มินัลที่กลับด้านผ่านตัวต้านทาน $R_{1}$และสร้างเวอร์ชันขยายเป็นเอาต์พุต แอมพลิฟายเออร์นี้ไม่เพียง แต่ขยายอินพุตเท่านั้น แต่ยังกลับด้านด้วย (เปลี่ยนสัญลักษณ์)

circuit diagram ของแอมพลิฟายเออร์แบบกลับด้านจะแสดงในรูปต่อไปนี้ -

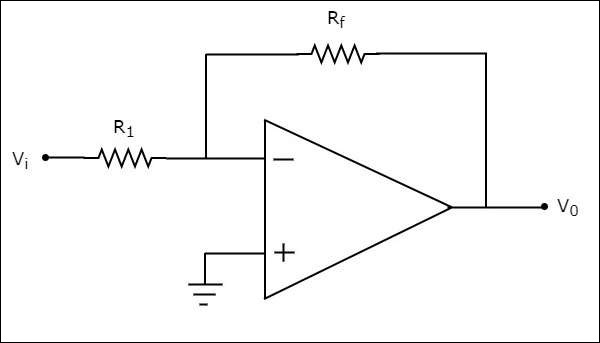
โปรดทราบว่าสำหรับ op-amp แรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านจะเท่ากับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ทางกายภาพไม่มีการสั้นระหว่างขั้วทั้งสอง แต่virtuallyพวกเขาอยู่ใน short ซึ่งกันและกัน

ในวงจรที่แสดงด้านบนขั้วอินพุตที่ไม่กลับด้านจะเชื่อมต่อกับกราวด์ นั่นหมายความว่าศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์

nodal equation ที่โหนดของเทอร์มินัลนี้ดังที่แสดงด้านล่าง -

$$\frac{0-V_i}{R_1}+ \frac{0-V_0}{R_f}=0$$

$$=>\frac{-V_i}{R_1}= \frac{V_0}{R_f}$$

$$=>V_{0}=\left(\frac{-R_f}{R_1}\right)V_{t}$$

$$=>\frac{V_0}{V_i}= \frac{-R_f}{R_1}$$

อัตราส่วนของแรงดันขาออก $V_{0}$ และแรงดันไฟฟ้าขาเข้า $V_{i}$คือแรงดันไฟฟ้าหรืออัตราขยายของเครื่องขยายเสียง ดังนั้นไฟล์gain of inverting amplifier เท่ากับ $-\frac{R_f}{R_1}$.

โปรดทราบว่าอัตราขยายของแอมพลิฟายเออร์กลับด้านกำลังมีไฟล์ negative sign. แสดงว่ามีความแตกต่างของเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

เครื่องขยายเสียงแบบไม่กลับด้าน

แอมพลิฟายเออร์ที่ไม่กลับด้านจะรับอินพุตผ่านเทอร์มินัลที่ไม่กลับด้านและสร้างเวอร์ชันขยายเป็นเอาต์พุต ตามชื่อที่แนะนำแอมพลิฟายเออร์นี้จะขยายอินพุตโดยไม่ต้องกลับด้านหรือเปลี่ยนสัญลักษณ์ของเอาต์พุต

circuit diagram ของเครื่องขยายเสียงที่ไม่กลับด้านจะแสดงในรูปต่อไปนี้ -

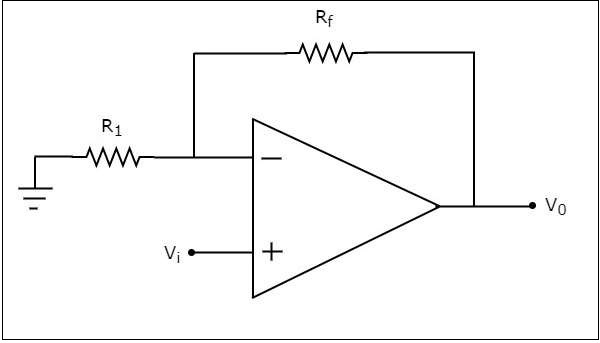
ในวงจรข้างต้นแรงดันไฟฟ้าขาเข้า $V_{i}$ถูกนำไปใช้โดยตรงกับขั้วอินพุตที่ไม่กลับด้านของ op-amp ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเป็น$V_{i}$.

โดยใช้ voltage division principleเราสามารถคำนวณแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp ดังที่แสดงด้านล่าง -

$$=>V_{1} = V_{0}\left(\frac{R_1}{R_1+R_f}\right)$$

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเหมือนกับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน

$$=>V_{1} = V_{i}$$

$$=>V_{0}\left(\frac{R_1}{R_1+R_f}\right)=V_{i}$$

$$=>\frac{V_0}{V_i}=\frac{R_1+R_f}{R_1}$$

$$=>\frac{V_0}{V_i}=1+\frac{R_f}{R_1}$$

ตอนนี้อัตราส่วนของแรงดันขาออก $V_{0}$ และแรงดันไฟฟ้าขาเข้า $V_{i}$ หรือแรงดันไฟฟ้าหรือ gain of the non-inverting amplifier เท่ากับ $1+\frac{R_f}{R_1}$.

โปรดทราบว่าอัตราขยายของแอมพลิฟายเออร์ที่ไม่กลับด้านกำลังมีไฟล์ positive sign. แสดงว่าไม่มีความแตกต่างของเฟสระหว่างอินพุตและเอาต์พุต

ผู้ติดตามแรงดันไฟฟ้า

ก voltage followerเป็นวงจรอิเล็กทรอนิกส์ซึ่งสร้างเอาต์พุตตามแรงดันไฟฟ้าขาเข้า เป็นกรณีพิเศษของเครื่องขยายเสียงที่ไม่กลับด้าน

หากเราพิจารณาค่าของตัวต้านทานแบบป้อนกลับ $R_{f}$เป็นศูนย์โอห์มและ (หรือ) ค่าของตัวต้านทาน 1 เป็นอินฟินิตี้โอห์มจากนั้นแอมพลิฟายเออร์ที่ไม่กลับด้านจะกลายเป็นตัวติดตามแรงดันไฟฟ้า circuit diagram ของตัวติดตามแรงดันไฟฟ้าแสดงในรูปต่อไปนี้ -

ในวงจรข้างต้นแรงดันไฟฟ้าขาเข้า $V_{i}$ถูกนำไปใช้โดยตรงกับขั้วอินพุตที่ไม่กลับด้านของ op-amp ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp จึงเท่ากับ$V_{i}$. ที่นี่เอาต์พุตจะเชื่อมต่อโดยตรงกับขั้วอินพุตที่กลับด้านของ opamp ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จึงเท่ากับ$V_{0}$.

$$=>V_{0} = V_{i}$$

ดังนั้นแรงดันขาออก $V_{0}$ ของตัวติดตามแรงดันไฟฟ้าเท่ากับแรงดันไฟฟ้าขาเข้า $V_{i}$.

ดังนั้นไฟล์ gain of a voltage follower มีค่าเท่ากับหนึ่งตั้งแต่แรงดันขาออกทั้งสอง $V_{0}$ และแรงดันไฟฟ้าขาเข้า $V_{i}$ ของผู้ติดตามแรงดันไฟฟ้าเหมือนกัน

ในบทที่แล้วเราได้กล่าวถึงการใช้งานพื้นฐานของ op-amp โปรดทราบว่าพวกมันอยู่ภายใต้การดำเนินการเชิงเส้นของ op-amp ในบทนี้ให้เราพูดคุยเกี่ยวกับวงจรเลขคณิตซึ่งเป็นแอปพลิเคชันเชิงเส้นของ op-amp

วงจรอิเล็กทรอนิกส์ซึ่งทำหน้าที่ทางคณิตศาสตร์เรียกว่าเป็น arithmetic circuits. การใช้ออปแอมป์คุณสามารถสร้างวงจรเลขคณิตพื้นฐานเช่นไฟล์adder และก subtractor. ในบทนี้คุณจะได้เรียนรู้เกี่ยวกับแต่ละข้อโดยละเอียด

แอดเดอร์

Adder เป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งเท่ากับผลรวมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงวงจรแอดเดอร์ที่ใช้ op-amp

adder ที่ใช้ op-amp จะสร้างเอาต์พุตเท่ากับผลรวมของแรงดันไฟฟ้าอินพุตที่ใช้ที่ขั้วต่อกลับด้าน เรียกอีกอย่างว่าเป็นsumming amplifierเนื่องจากเอาต์พุตเป็นแบบขยาย

circuit diagram ของ adder ที่ใช้ op-amp จะแสดงในรูปต่อไปนี้ -

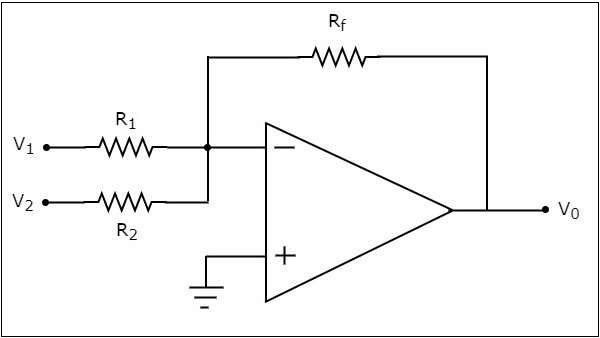
ในวงจรข้างต้นขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเชื่อมต่อกับกราวด์ นั่นหมายถึงศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้าน

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเหมือนกับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์

nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ

$$\frac{0-V_1}{R_1}+\frac{0-V_2}{R_2}+\frac{0-V_0}{R_f}=0$$

$$=>\frac{V_1}{R_1}-\frac{V_2}{R_2}=\frac{V_0}{R_f}$$

$$=>V_{0}=R_{f}\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}\right)$$

ถ้า $R_{f}=R_{1}=R_{2}=R$แล้วแรงดันไฟฟ้าขาออก $V_{0}$ จะเป็น -

$$V_{0}=-R{}\left(\frac{V_1}{R}+\frac{V_2}{R}\right)$$

$$=>V_{0}=-(V_{1}+V_{2})$$

ดังนั้นวงจร adder ที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างผลรวมของแรงดันไฟฟ้าอินพุตสองตัว $v_{1}$ และ $v_{1}$ในฐานะเอาต์พุตเมื่อตัวต้านทานทั้งหมดที่มีอยู่ในวงจรมีค่าเท่ากัน โปรดทราบว่าแรงดันไฟฟ้าขาออก$V_{0}$ ของวงจรแอดเดอร์กำลังมี negative signซึ่งบ่งชี้ว่ามีความแตกต่างของเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

ตัวลบ

ตัวลบเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งเท่ากับผลต่างของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงวงจรตัวลบที่ใช้ op-amp

ตัวลบที่ใช้ op-amp จะสร้างเอาต์พุตเท่ากับความแตกต่างของแรงดันไฟฟ้าอินพุตที่ใช้ที่ขั้วต่อกลับด้านและไม่กลับด้าน เรียกอีกอย่างว่าเป็นdifference amplifierเนื่องจากเอาต์พุตเป็นแบบขยาย

circuit diagram ของตัวลบที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

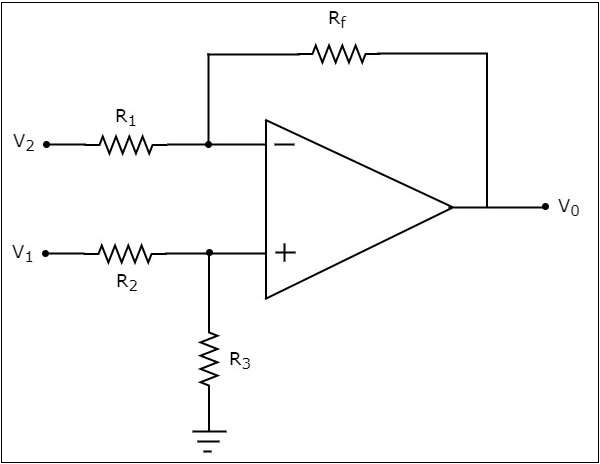
ตอนนี้ให้เราค้นหานิพจน์สำหรับแรงดันไฟฟ้าขาออก $V_{0}$ ของวงจรข้างต้นโดยใช้ superposition theorem โดยใช้ขั้นตอนต่อไปนี้ -

ขั้นตอนที่ 1

ประการแรกให้เราคำนวณแรงดันขาออก $V_{01}$ โดยพิจารณาเท่านั้น $V_{1}$.

สำหรับสิ่งนี้ให้กำจัด $V_{2}$โดยทำให้ไฟฟ้าลัดวงจร จากนั้นเราจะได้รับmodified circuit diagram ดังแสดงในรูปต่อไปนี้ -

ตอนนี้ใช้ไฟล์ voltage division principleคำนวณแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp

$$=>V_{p}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)$$

ตอนนี้วงจรข้างต้นดูเหมือนเครื่องขยายเสียงที่ไม่มีการกลับด้านที่มีแรงดันไฟฟ้าอินพุต $V_{p}$. ดังนั้นแรงดันขาออก$V_{01}$ ของวงจรข้างต้นจะเป็น

$$V_{01}=V_{p}\left(1+\frac{R_f}{R_1}\right)$$

แทนค่าของ $V_{p}$ ในสมการข้างต้นเราได้รับแรงดันไฟฟ้าขาออก $V_{01}$ โดยพิจารณาเท่านั้น $V_{1}$, เป็น -

$$V_{01}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)$$

ขั้นตอนที่ 2

ในขั้นตอนนี้ให้เราหาแรงดันขาออก $V_{02}$ โดยพิจารณาเท่านั้น $V_{2}$. เช่นเดียวกับในขั้นตอนข้างต้นให้กำจัด$V_{1}$โดยทำให้ไฟฟ้าลัดวงจร modified circuit diagram แสดงดังรูปต่อไปนี้

คุณสามารถสังเกตได้ว่าแรงดันไฟฟ้าที่ขั้วอินพุตแบบไม่กลับด้านของ op-amp จะเป็นศูนย์โวลต์ หมายความว่าวงจรข้างต้นเป็นเพียงinverting op-amp. ดังนั้นแรงดันขาออก$V_{02}$ ของวงจรข้างต้นจะเป็น -

$$V_{02}=\left(-\frac{R_f}{R_1}\right)V_{2}$$

ขั้นตอนที่ 3

ในขั้นตอนนี้เราจะได้รับแรงดันไฟฟ้าขาออก $V_{0}$ ของวงจรลบโดย adding the output voltagesได้รับในขั้นตอนที่ 1 และขั้นตอนที่ 2 ในทางคณิตศาสตร์สามารถเขียนเป็น

$$V_{0}=V_{01}+V_{02}$$

การแทนที่ค่าของ $V_{01}$ และ $V_{02}$ ในสมการข้างต้นเราได้ -

$$V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)+\left(-\frac{R_f}{R_1}\right)V_{2}$$

$$=>V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)-\left(\frac{R_f}{R_1}\right)V_{2}$$

ถ้า $R_{f}=R_{1}=R_{2}=R_{3}=R$แล้วแรงดันไฟฟ้าขาออก $V_{0}$ จะ

$$V_{0}=V_{1}\left(\frac{R}{R+R}\right)\left(1+\frac{R}{R}\right)-\left(\frac{R}{R}\right)V_{2}$$

$$=>V_{0}=V_{1}\left(\frac{R}{2R}\right)(2)-(1)V_{2}$$

$$V_{0}=V_{1}-V_{2}$$

ดังนั้นวงจรลบที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นความแตกต่างของแรงดันไฟฟ้าอินพุตสองตัว $V_{1}$ และ $V_{2}$เมื่อตัวต้านทานทั้งหมดที่มีอยู่ในวงจรมีค่าเท่ากัน

วงจรอิเล็กทรอนิกส์ที่ทำหน้าที่ทางคณิตศาสตร์เช่นการแยกความแตกต่างและการรวมเรียกว่าตัวแตกต่างและตัวรวมตามลำดับ

บทนี้จะกล่าวถึงรายละเอียดเกี่ยวกับ op-amp differentiatorและผู้รวมระบบ โปรดทราบว่าสิ่งเหล่านี้มาจากการใช้งานเชิงเส้นของ op-amp ด้วย

ความแตกต่าง

ก differentiatorเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตเท่ากับอนุพันธ์แรกของอินพุต ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับตัวแยกความแตกต่างที่ใช้ op-amp

ตัวแยกความแตกต่างที่ใช้ op-amp จะสร้างเอาต์พุตซึ่งเท่ากับความแตกต่างของแรงดันไฟฟ้าขาเข้าที่ใช้กับขั้วต่อกลับด้าน circuit diagram ของตัวแตกต่างที่ใช้ op-amp จะแสดงในรูปต่อไปนี้ -

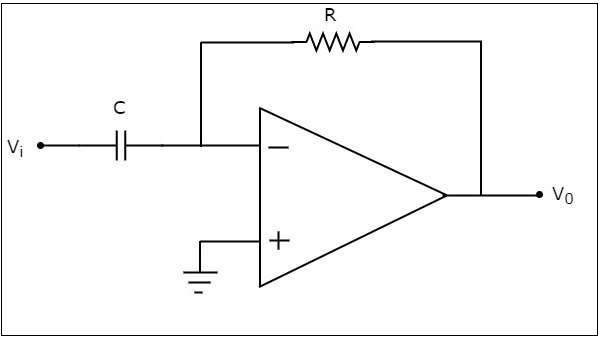
ในวงจรข้างต้นขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเชื่อมต่อกับกราวด์ นั่นหมายความว่าศูนย์โวลต์ถูกนำไปใช้กับเทอร์มินัลอินพุตที่ไม่กลับด้าน

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ opamp จะเท่ากับแรงดันไฟฟ้าที่มีอยู่ที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์

สมการปมที่โหนดของขั้วอินพุตกลับด้านคือ -

$$C\frac{\text{d}(0-V_{i})}{\text{d}t}+\frac{0-V_0}{R}=0$$

$$=>-C\frac{\text{d}V_{i}}{\text{d}t}=\frac{V_0}{R}$$

$$=>V_{0}=-RC\frac{\text{d}V_{i}}{\text{d}t}$$

ถ้า $RC=1\sec$แล้วแรงดันไฟฟ้าขาออก $V_{0}$ จะเป็น -

$$V_{0}=-\frac{\text{d}V_{i}}{\text{d}t}$$

ดังนั้นวงจรตัวแยกความแตกต่างที่ใช้ op-amp ที่แสดงด้านบนจะสร้างเอาต์พุตซึ่งเป็นความแตกต่างของแรงดันไฟฟ้าขาเข้า $V_{i}$เมื่อขนาดของอิมพีแดนซ์ของตัวต้านทานและตัวเก็บประจุต่างกัน

โปรดทราบว่าแรงดันไฟฟ้าขาออก $V_{0}$ กำลังมีไฟล์ negative signซึ่งบ่งชี้ว่ามีความแตกต่างของเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

อินทิเกรเตอร์

อัน integratorเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งเป็นการรวมอินพุตที่ใช้ ส่วนนี้กล่าวถึงเกี่ยวกับตัวรวมที่ใช้ op-amp

อินทิเกรเตอร์ที่ใช้ op-amp จะสร้างเอาต์พุตซึ่งเป็นอินทิกรัลของแรงดันไฟฟ้าอินพุตที่ใช้กับเทอร์มินอลกลับด้าน circuit diagram ของตัวรวมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

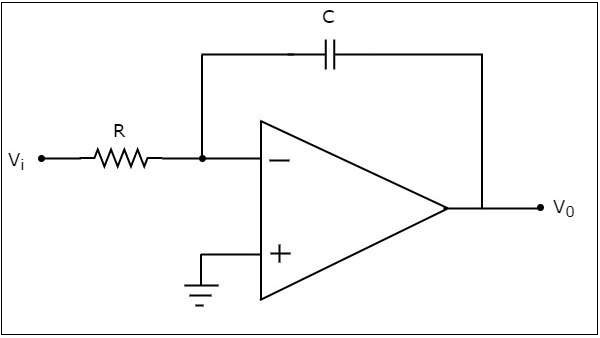
ในวงจรที่แสดงด้านบนขั้วอินพุตที่ไม่กลับด้านของ op-amp เชื่อมต่อกับกราวด์ นั่นหมายความว่าศูนย์โวลต์ถูกนำไปใช้กับเทอร์มินัลอินพุตที่ไม่กลับด้าน

ตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเท่ากับแรงดันไฟฟ้าที่มีอยู่ที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์

nodal equation ที่ขั้วอินพุตกลับด้านคือ -

$$\frac{0-V_i}{R}+C\frac{\text{d}(0-V_{0})}{\text{d}t}=0$$

$$=>\frac{-V_i}{R}=C\frac{\text{d}V_{0}}{\text{d}t}$$

$$=>\frac{\text{d}V_{0}}{\text{d}t}=-\frac{V_i}{RC}$$

$$=>{d}V_{0}=\left(-\frac{V_i}{RC}\right){\text{d}t}$$

การรวมทั้งสองด้านของสมการที่แสดงด้านบนเราได้ -

$$\int{d}V_{0}=\int\left(-\frac{V_i}{RC}\right){\text{d}t}$$

$$=>V_{0}=-\frac{1}{RC}\int V_{t}{\text{d}t}$$

ถ้า $RC=1\sec$จากนั้นแรงดันไฟฟ้าขาออก $V_{0}$ จะเป็น -

$$V_{0}=-\int V_{i}{\text{d}t}$$

ดังนั้นวงจรอินทิเกรเตอร์ที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นอินทิกรัลของแรงดันไฟฟ้าขาเข้า $V_{i}$เมื่อขนาดของอิมพีแดนซ์ของตัวต้านทานและตัวเก็บประจุต่างกัน

Note - แรงดันขาออก $V_{0}$ กำลังมีไฟล์ negative signซึ่งระบุว่ามีความแตกต่างเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

แรงดันและกระแสเป็นปริมาณไฟฟ้าพื้นฐาน พวกเขาสามารถแปลงเป็นกันและกันได้ขึ้นอยู่กับความต้องการVoltage to Current Converter และปัจจุบันเป็น Voltage Converterเป็นสองวงจรที่ช่วยในการแปลงดังกล่าว นอกจากนี้ยังเป็นการใช้งานเชิงเส้นของ op-amps บทนี้จะกล่าวถึงรายละเอียด

แรงดันเป็นตัวแปลงปัจจุบัน

ก voltage to current converter หรือ V to I converterเป็นวงจรอิเล็กทรอนิกส์ที่รับกระแสเป็นอินพุตและสร้างแรงดันไฟฟ้าเป็นเอาต์พุต ส่วนนี้จะกล่าวถึงเกี่ยวกับแรงดันไฟฟ้าที่ใช้ op-amp เป็นตัวแปลงกระแส

แรงดันไฟฟ้าที่ใช้ op-amp เป็นตัวแปลงกระแสจะสร้างกระแสไฟฟ้าขาออกเมื่อใช้แรงดันไฟฟ้ากับขั้วที่ไม่กลับหัว circuit diagram ของแรงดันไฟฟ้าที่ใช้แอมป์เป็นตัวแปลงกระแสจะแสดงในรูปต่อไปนี้

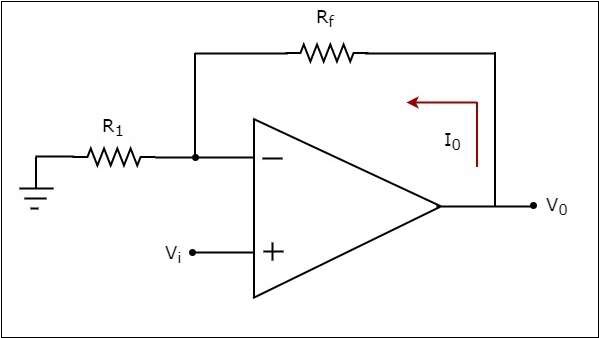
ในวงจรที่แสดงด้านบนแรงดันไฟฟ้าขาเข้า $V_{i}$ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp ให้เป็นไปตามvirtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุทอินพุทของออปแอมป์จะเท่ากับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็น$V_{i}$.

nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ -

$$\frac{V_i}{R_1}-I_{0}=0$$

$$=>I_{0}=\frac{V_t}{R_1}$$

ดังนั้นไฟล์ output current $I_{0}$ ของแรงดันไฟฟ้าต่อตัวแปลงกระแสคืออัตราส่วนของแรงดันไฟฟ้าขาเข้า $V_{i}$ และความต้านทาน $R_{1}$.

เราสามารถเขียนสมการข้างต้นใหม่ได้เป็น -

$$\frac{I_0}{V_i}=\frac{1}{R_1}$$

สมการข้างต้นแสดงถึงอัตราส่วนของกระแสไฟฟ้าขาออก $I_{0}$ และแรงดันไฟฟ้าขาเข้า $V_{i}$ & มันก็เท่ากับความต้านทานซึ่งกันและกัน $R_{1}$ อัตราส่วนของกระแสไฟขาออก $I_{0}$ และแรงดันไฟฟ้าขาเข้า $V_{i}$ เรียกว่าเป็น Transconductance.

เรารู้ว่าอัตราส่วนของเอาต์พุตและอินพุตของวงจรเรียกว่าเป็นกำไร ดังนั้นการได้รับของแรงดันไฟฟ้าเป็นตัวแปลงกระแสคือ Transconductance และมันจะเท่ากับความต้านทานซึ่งกันและกัน$R_{1}$.

ปัจจุบันเป็นตัวแปลงแรงดันไฟฟ้า

ก current to voltage converter หรือ I to V converterเป็นวงจรอิเล็กทรอนิกส์ที่รับกระแสเป็นอินพุตและสร้างแรงดันไฟฟ้าเป็นเอาต์พุต ส่วนนี้กล่าวถึงเกี่ยวกับตัวแปลงกระแสไฟฟ้าที่ใช้แอมป์เป็นตัวแปลงแรงดันไฟฟ้า

กระแสไฟฟ้าที่ใช้แอมป์เป็นตัวแปลงแรงดันไฟฟ้าจะสร้างแรงดันไฟฟ้าขาออกเมื่อกระแสไฟฟ้าถูกนำไปใช้กับขั้วต่อกลับด้าน circuit diagram ของกระแสไฟฟ้าที่ใช้แอมป์เป็นตัวแปลงแรงดันไฟฟ้าแสดงในรูปต่อไปนี้

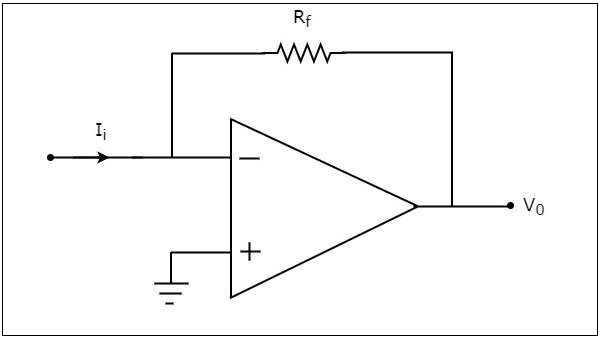
ในวงจรที่แสดงด้านบนขั้วอินพุตที่ไม่กลับด้านของ op-amp เชื่อมต่อกับกราวด์ นั่นหมายถึงศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้าน

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุทอินพุทของออปแอมป์จะเท่ากับแรงดันไฟฟ้าที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเป็นศูนย์โวลต์

nodal equation ที่โหนดของขั้วกลับด้านคือ -

$$-I_{i}+\frac{0-V_0}{R_f}=0$$

$$-I_{i}=\frac{V_0}{R_f}$$

$$V_{0}=-R_{t}I_{i}$$

ดังนั้นไฟล์ output voltage, $V_{0}$ ของตัวแปลงกระแสเป็นแรงดันเป็นผลิตภัณฑ์ (ลบ) ของความต้านทานข้อเสนอแนะ $R_{f}$ และอินพุตปัจจุบัน $I_{t}$. สังเกตว่าแรงดันขาออก$V_{0}$ กำลังมีไฟล์ negative signซึ่งบ่งชี้ว่ามีความแตกต่างของเฟส180 ⁰ระหว่างกระแสอินพุตและแรงดันไฟฟ้าขาออก

เราสามารถเขียนสมการข้างต้นใหม่ได้เป็น -

$$\frac{V_0}{I_i}=-R_{f}$$

สมการข้างต้นแสดงถึงอัตราส่วนของแรงดันไฟฟ้าขาออก $V_{0}$ และอินพุตปัจจุบัน $I_{i}$และเท่ากับผลลบของความต้านทานข้อเสนอแนะ $R_{f}$. อัตราส่วนของแรงดันขาออก$V_{0}$ และอินพุตปัจจุบัน $I_{i}$ เรียกว่าเป็น Transresistance.

เรารู้ว่าอัตราส่วนของเอาต์พุตและอินพุตของวงจรเรียกว่าเป็น gain. ดังนั้นการได้รับของตัวแปลงกระแสเป็นแรงดันไฟฟ้าคือความต้านทานทรานส์และเท่ากับความต้านทานป้อนกลับ (ลบ)$R_{f}$ .

ก comparatorเป็นวงจรอิเล็กทรอนิกส์ซึ่งเปรียบเทียบอินพุตสองตัวที่ใช้กับมันและสร้างเอาต์พุต ค่าเอาต์พุตของตัวเปรียบเทียบจะระบุว่าอินพุตใดมากกว่าหรือน้อยกว่า โปรดทราบว่าตัวเปรียบเทียบอยู่ภายใต้การใช้งาน IC ที่ไม่ใช่เชิงเส้น

op-amp ประกอบด้วยขั้วอินพุตสองขั้วและด้วยเหตุนี้ตัวเปรียบเทียบที่ใช้ op-amp จะเปรียบเทียบอินพุตสองตัวที่ใช้กับมันและสร้างผลลัพธ์ของการเปรียบเทียบเป็นเอาต์พุต ในบทนี้จะกล่าวถึงop-amp based comparators.

ประเภทของเครื่องเปรียบเทียบ

เครื่องเปรียบเทียบมีสองประเภท: Inverting และ Non-inverting. ส่วนนี้จะกล่าวถึงรายละเอียดทั้งสองประเภทนี้

Inverting Comparator

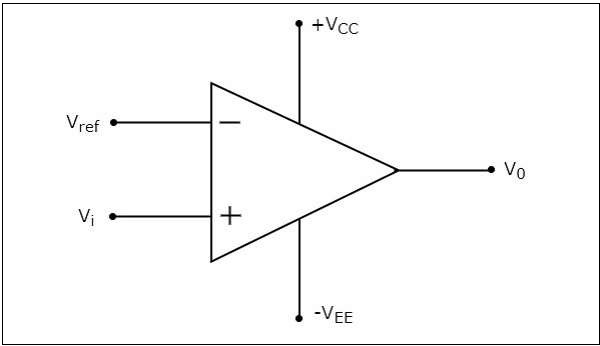
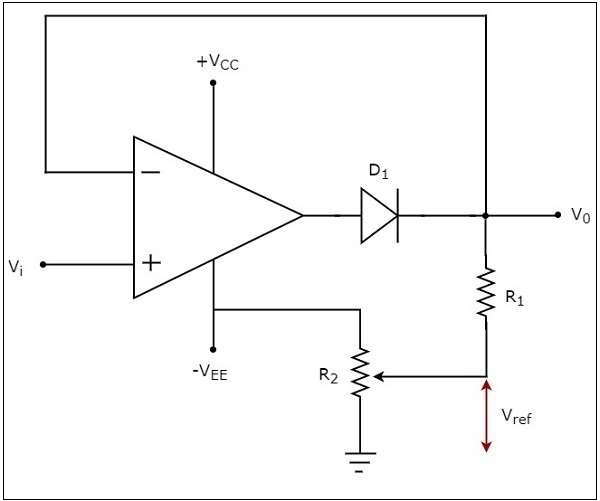
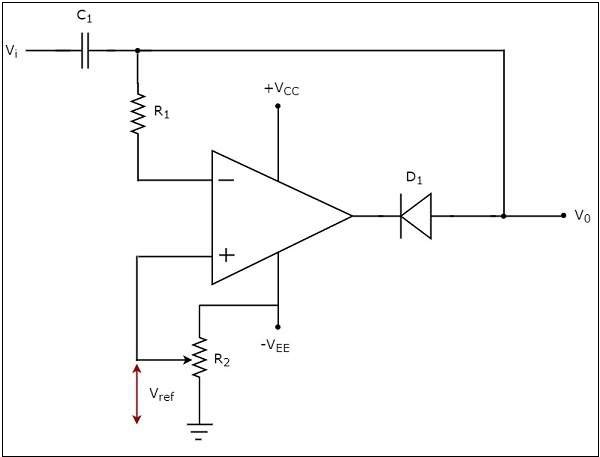
อัน inverting comparatorเป็นเครื่องเปรียบเทียบแบบใช้ op-amp ซึ่งใช้แรงดันไฟฟ้าอ้างอิงกับเทอร์มินัลที่ไม่กลับด้านและแรงดันไฟฟ้าเข้าจะถูกนำไปใช้กับขั้วต่อกลับด้าน ตัวเปรียบเทียบนี้เรียกว่า asinverting ตัวเปรียบเทียบเนื่องจากแรงดันไฟฟ้าขาเข้าซึ่งต้องเปรียบเทียบถูกนำไปใช้กับขั้วกลับด้านของ op-amp

circuit diagram ของตัวเปรียบเทียบการกลับด้านจะแสดงในรูปต่อไปนี้

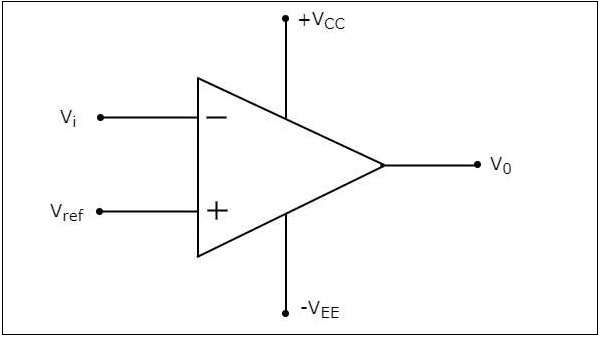
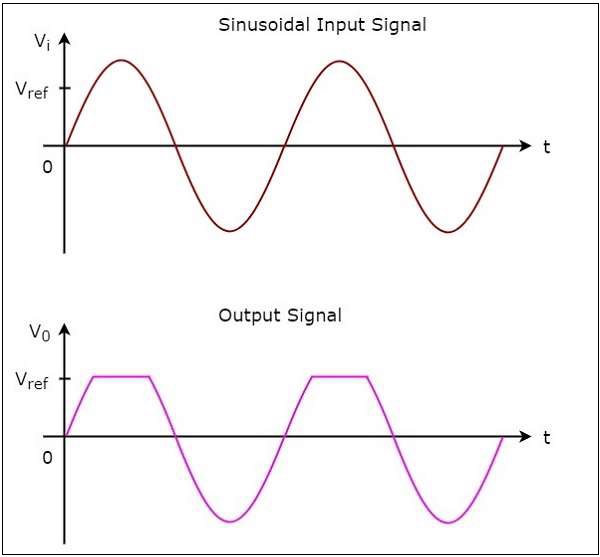
operationของตัวเปรียบเทียบกลับด้านนั้นง่ายมาก มันก่อให้เกิดค่าหนึ่งในสองค่า$+V_{sat}$ และ $-V_{sat}$ ที่เอาต์พุตขึ้นอยู่กับค่าของแรงดันไฟฟ้าขาเข้า $V_{i}$ และแรงดันไฟฟ้าอ้างอิง $V_{ref}$.

ค่าเอาต์พุตของตัวเปรียบเทียบกลับด้านจะเป็น $-V_{sat}$ซึ่งการป้อนข้อมูล $V_{i}$ แรงดันไฟฟ้ามากกว่าแรงดันอ้างอิง $V_{ref}$.
ค่าเอาต์พุตของตัวเปรียบเทียบกลับด้านจะเป็น $+V_{sat}$ซึ่งการป้อนข้อมูล $V_{i}$ น้อยกว่าแรงดันอ้างอิง $V_{ref}$.

ตัวอย่าง

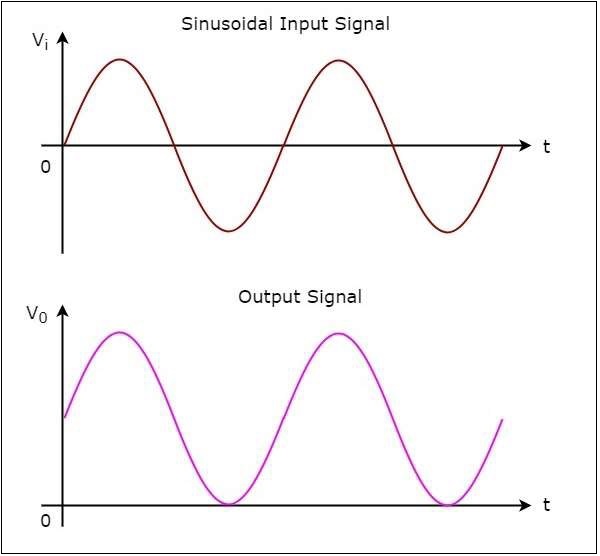
ให้เราวาดไฟล์ output wave form ของตัวเปรียบเทียบกลับด้านเมื่อสัญญาณอินพุตไซน์และแรงดันอ้างอิงศูนย์โวลต์ถูกนำไปใช้กับขั้วต่อกลับด้านและไม่กลับด้านตามลำดับ

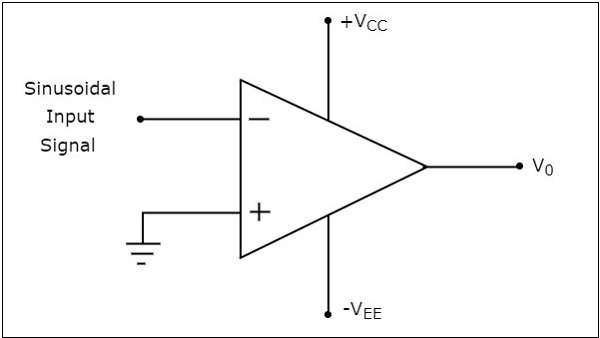
operation ของตัวเปรียบเทียบการกลับด้านที่แสดงไว้ด้านบนจะกล่าวถึงด้านล่าง -

ในช่วง positive half cycleของสัญญาณอินพุตรูปไซน์แรงดันไฟฟ้าที่ขั้วต่อกลับของ op-amp มีค่ามากกว่าศูนย์โวลต์ ดังนั้นค่าเอาต์พุตของตัวเปรียบเทียบกลับด้านจะเท่ากับ$-V_{sat}$ ในช่วงครึ่งรอบบวกของสัญญาณอินพุตไซน์
ในทำนองเดียวกันในช่วง negative half cycleของสัญญาณอินพุตรูปไซน์แรงดันไฟฟ้าที่ขั้วกลับด้านของ op-amp มีค่าน้อยกว่าศูนย์โวลต์ ดังนั้นค่าเอาต์พุตของตัวเปรียบเทียบกลับด้านจะเท่ากับ$+V_{sat}$ ในช่วงครึ่งรอบที่เป็นลบของสัญญาณอินพุตไซน์

รูปต่อไปนี้แสดงไฟล์ input and output waveforms ของตัวเปรียบเทียบกลับด้านเมื่อแรงดันอ้างอิงเป็นศูนย์โวลต์

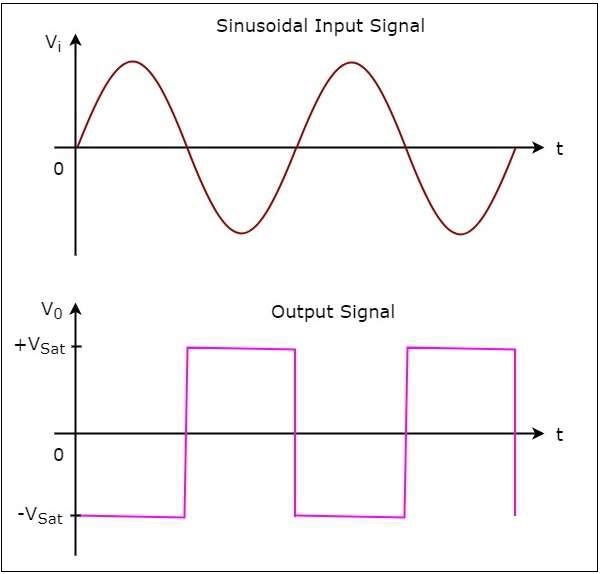
ในรูปที่แสดงด้านบนเราสามารถสังเกตได้ว่าการเปลี่ยนเอาต์พุตจาก $-V_{sat}$ ถึง $+V_{sat}$ หรือจาก $+V_{sat}$ ถึง $-V_{sat}$เมื่อใดก็ตามที่สัญญาณอินพุตไซน์ข้ามศูนย์โวลต์ กล่าวอีกนัยหนึ่งเอาต์พุตจะเปลี่ยนค่าเมื่ออินพุตข้ามศูนย์โวลต์ ดังนั้นวงจรข้างต้นจึงเรียกอีกอย่างว่าinverting zero crossing detector.

ตัวเปรียบเทียบแบบไม่เปลี่ยนกลับ

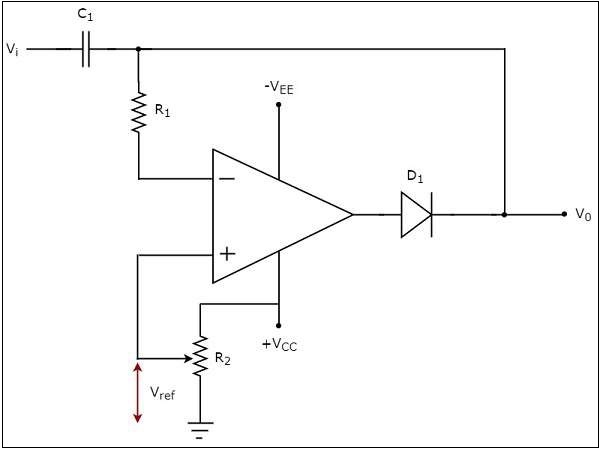
ตัวเปรียบเทียบแบบไม่กลับด้านคือตัวเปรียบเทียบแบบใช้ op-amp ซึ่งใช้แรงดันอ้างอิงกับเทอร์มินัลกลับด้านและแรงดันไฟฟ้าอินพุตจะถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้าน ตัวเปรียบเทียบที่ใช้ op-amp นี้เรียกว่าเป็นnon-inverting ตัวเปรียบเทียบเนื่องจากแรงดันไฟฟ้าขาเข้าซึ่งจะต้องเปรียบเทียบถูกนำไปใช้กับขั้วที่ไม่กลับด้านของ op-amp

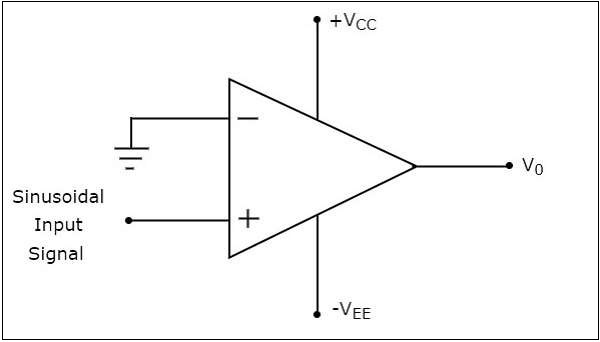
circuit diagram ของตัวเปรียบเทียบแบบไม่กลับด้านจะแสดงในรูปต่อไปนี้

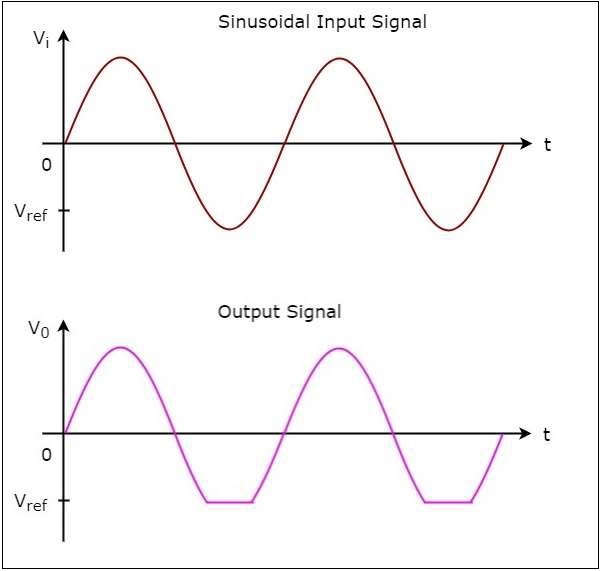
operationของตัวเปรียบเทียบแบบไม่กลับด้านนั้นง่ายมาก มันก่อให้เกิดค่าหนึ่งในสองค่า$+V_{sat}$ และ $-V_{sat}$ ที่เอาต์พุตตามค่าของแรงดันไฟฟ้าขาเข้า $V_{t}$ และแรงดันไฟฟ้าอ้างอิง $+V_{ref}$.

ค่าเอาต์พุตของตัวเปรียบเทียบที่ไม่กลับด้านจะเป็น $+V_{sat}$ซึ่งแรงดันไฟฟ้าขาเข้า $V_{i}$ มากกว่าแรงดันอ้างอิง $+V_{ref}$.
ค่าเอาต์พุตของตัวเปรียบเทียบแบบไม่กลับด้านจะผึ้ง $-V_{sat}$ซึ่งแรงดันไฟฟ้าขาเข้า $V_{i}$ น้อยกว่าแรงดันอ้างอิง $+V_{ref}$.

ตัวอย่าง

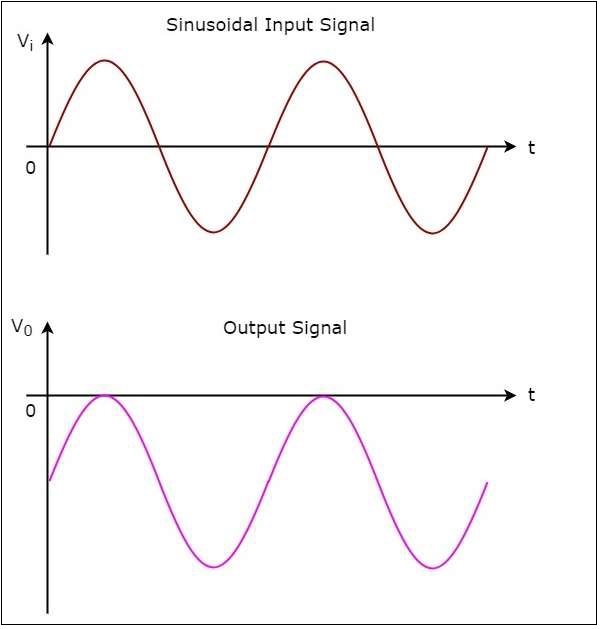
ให้เราวาดไฟล์ output wave form ของตัวเปรียบเทียบที่ไม่กลับด้านเมื่อสัญญาณอินพุตไซน์และแรงดันอ้างอิงที่เป็นศูนย์โวลต์ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านและกลับด้านของ op-amp ตามลำดับ

operation ของตัวเปรียบเทียบแบบไม่กลับด้านมีอธิบายไว้ด้านล่าง -

ในช่วง positive half cycleของสัญญาณอินพุตรูปไซน์แรงดันไฟฟ้าที่ขั้วที่ไม่กลับด้านของ op-amp มีค่ามากกว่าศูนย์โวลต์ ดังนั้นค่าเอาต์พุตของตัวเปรียบเทียบที่ไม่กลับด้านจะเท่ากับ$+V_{sat}$ ในช่วงครึ่งรอบบวกของสัญญาณอินพุตไซน์
ในทำนองเดียวกันในช่วง negative half cycleของสัญญาณอินพุตรูปไซน์แรงดันไฟฟ้าที่ขั้วที่ไม่กลับด้านของ op-amp มีค่าน้อยกว่าศูนย์โวลต์ ดังนั้นค่าเอาต์พุตของตัวเปรียบเทียบที่ไม่กลับด้านจะเท่ากับ$-V_{sat}$ ในช่วงครึ่งรอบที่เป็นลบของสัญญาณอินพุตไซน์

รูปต่อไปนี้แสดงไฟล์ input and output waveforms ของตัวเปรียบเทียบแบบไม่กลับด้านเมื่อแรงดันอ้างอิงเป็นศูนย์โวลต์

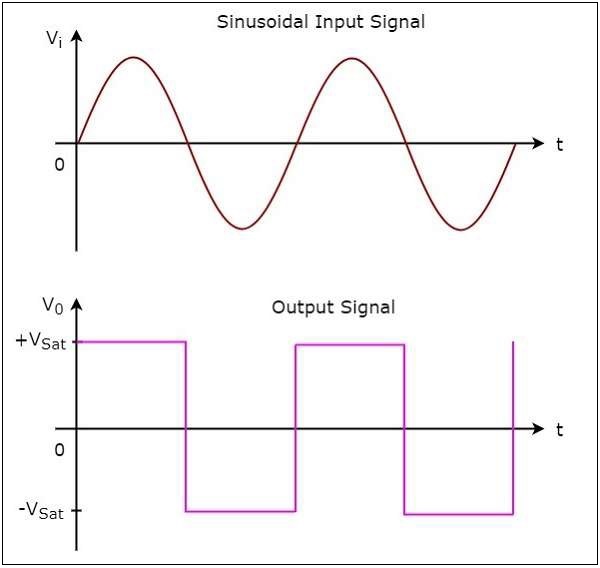
จากรูปที่แสดงด้านบนเราสามารถสังเกตได้ว่าการเปลี่ยนเอาต์พุตทั้งจาก $+V_{sat}$ ถึง $-V_{sat}$ หรือจาก $-V_{sat}$ ถึง $+V_{sat}$เมื่อใดก็ตามที่สัญญาณอินพุตไซน์ข้ามศูนย์โวลต์ นั่นหมายความว่าเอาต์พุตจะเปลี่ยนค่าเมื่ออินพุตข้ามศูนย์โวลต์ ดังนั้นวงจรข้างต้นจึงเรียกอีกอย่างว่าnon-inverting zero crossing detector.

วงจรอิเล็กทรอนิกส์ที่ดำเนินการทางคณิตศาสตร์เช่นลอการิทึมและต่อต้านลอการิทึม (เลขชี้กำลัง) ที่มีการขยายสัญญาณเรียกว่า Logarithmic amplifier และ Anti-Logarithmic amplifier ตามลำดับ

ในบทนี้จะกล่าวถึงไฟล์ Logarithmic amplifier และ Anti-Logarithmic amplifierในรายละเอียด. โปรดทราบว่าเครื่องขยายเสียงเหล่านี้อยู่ภายใต้การใช้งานที่ไม่ใช่เชิงเส้น

เครื่องขยายเสียงลอการิทึม

ก logarithmic amplifierหรือก log amplifierเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตที่เป็นสัดส่วนกับลอการิทึมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับแอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp

แอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp จะสร้างแรงดันไฟฟ้าที่เอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมของแรงดันไฟฟ้าที่ใช้กับตัวต้านทานที่เชื่อมต่อกับขั้วกลับด้าน circuit diagram ของแอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

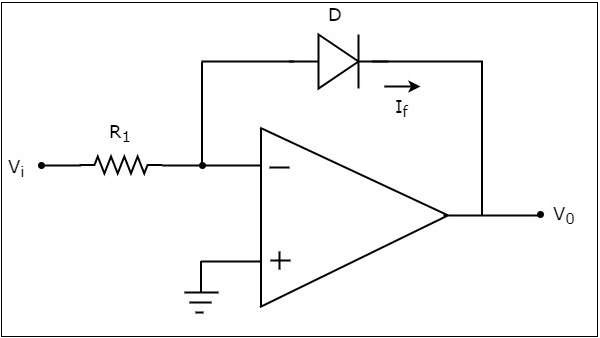
ในวงจรข้างต้นขั้วอินพุตที่ไม่กลับด้านของ op-amp จะเชื่อมต่อกับกราวด์ นั่นหมายความว่าศูนย์โวลต์ถูกนำไปใช้ที่ขั้วอินพุตที่ไม่กลับด้านของ op-amp

nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ -

$$\frac{0-V_i}{R_1}+I_{f}=0$$

$$=>I_{f}=\frac{V_i}{R_1}......Equation 1$$

ต่อไปนี้คือไฟล์ equation for current ไหลผ่านไดโอดเมื่ออยู่ในอคติไปข้างหน้า -

$$I_{f}=I_{s} e^{(\frac{V_f}{nV_T})} ......Equation 2$$

ที่ไหน

$I_{s}$ คือกระแสอิ่มตัวของไดโอด

$V_{f}$ คือแรงดันตกคร่อมไดโอดเมื่ออยู่ในอคติไปข้างหน้า

$V_{T}$ คือแรงดันไฟฟ้าเทียบเท่าความร้อนของไดโอด

KVL equation รอบ ๆ ข้อเสนอแนะของ op amp จะเป็น -

$$0-V_{f}-V_{0}=0$$

$$=>V_{f}=-V_{0}$$

การแทนที่ค่าของ $V_{f}$ ในสมการ 2 เราได้ -

$$I_{f}=I_{s} e^{\left(\frac{-V_0}{nV_T}\right)} ......Equation 3$$

สังเกตว่าเงื่อนไขด้านซ้ายมือของทั้งสมการ 1 และสมการ 3 เหมือนกัน ดังนั้นจึงถือสมการทางด้านขวามือของทั้งสองสมการดังที่แสดงด้านล่าง -

$$\frac{V_i}{R_1}=I_{s}e^{\left(\frac{-V_0}{nV_T}\right)}$$

$$\frac{V_i}{R_1I_s}= e^{\left(\frac{-V_0}{nV_T}\right)}$$

การสมัคร natural logarithm ทั้งสองด้านเราได้รับ -

$$In\left(\frac{V_i}{R_1I_s}\right)= \frac{-V_0}{nV_T}$$

$$V_{0}=-{nV_T}In\left(\frac{V_i}{R_1I_s}\right)$$

โปรดสังเกตว่าในสมการข้างต้นพารามิเตอร์ n ${V_T}$ และ $I_{s}$คือค่าคงที่ ดังนั้นแรงดันขาออก$V_{0}$ จะเป็นสัดส่วนกับ natural logarithm ของแรงดันไฟฟ้าขาเข้า $V_{i}$ สำหรับค่าความต้านทานคงที่ $R_{1}$.

ดังนั้นวงจรแอมพลิฟายเออร์ลอการิทึมที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมธรรมชาติของแรงดันไฟฟ้าอินพุต ${V_T}$, เมื่อไหร่ ${R_1I_s}=1V$.

สังเกตว่าแรงดันขาออก $V_{0}$ มี negative signซึ่งบ่งชี้ว่ามีความแตกต่างของเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

แอมพลิฟายเออร์ต่อต้านลอการิทึม

อัน anti-logarithmic amplifierหรือ anti-log amplifierเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตที่เป็นสัดส่วนกับค่าต่อต้านลอการิทึมของอินพุตที่ใช้ ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp

แอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp จะสร้างแรงดันไฟฟ้าที่เอาต์พุตซึ่งเป็นสัดส่วนกับค่าต่อต้านลอการิทึมของแรงดันไฟฟ้าที่ใช้กับไดโอดที่เชื่อมต่อกับขั้วกลับด้าน

circuit diagram ของแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

ในวงจรที่แสดงด้านบนขั้วอินพุตที่ไม่กลับด้านของ op-amp เชื่อมต่อกับกราวด์ หมายความว่าศูนย์โวลต์ถูกนำไปใช้กับขั้วอินพุตที่ไม่กลับด้าน

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ op-amp จะเท่ากับแรงดันไฟฟ้าที่มีอยู่ที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านจะเป็นศูนย์โวลต์

nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ -

$$-I_{f}+\frac{0-V_0}{R_f}=0$$

$$=>-\frac{V_0}{R_f}=I_{f}$$

$$=>V_{0}=-R_{f}I_{f}.........Equation 4$$

เรารู้ว่าสมการของกระแสที่ไหลผ่านไดโอดเมื่อมันอยู่ข้างหน้าไบแอสเป็นไปตามที่ระบุด้านล่าง -

$$I_{f}=I_{s} e^{\left(\frac{V_f}{nV_T}\right)}$$

การแทนที่ค่าของ $I_{f}$ ในสมการ 4 เราได้

$$V_{0}=-R_{f}\left \{{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}\right \}$$

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}......Equation 5$$

สมการ KVL ที่ด้านอินพุตของขั้วกลับด้านของ op amp จะเป็น

$$V_{i}-V_{f}=0$$

$$V_{f}=V_{i}$$

การแทนที่ค่าของสมการ 5 เราจะได้ -

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_i}{nV_T}\right)}}$$

โปรดสังเกตว่าในสมการข้างต้นพารามิเตอร์ n ${V_T}$ และ $I_{s}$คือค่าคงที่ ดังนั้นแรงดันขาออก${V_0}$ จะเป็นสัดส่วนกับ anti-natural logarithm (เลขชี้กำลัง) ของแรงดันไฟฟ้าขาเข้า ${V_i}$สำหรับค่าความต้านทานข้อเสนอแนะคงที่ ${R_f}$.

ดังนั้นวงจรแอมพลิฟายเออร์ต่อต้านลอการิทึมที่ใช้ op-amp ที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตซึ่งเป็นสัดส่วนกับลอการิทึมต่อต้านธรรมชาติ (เลขชี้กำลัง) ของแรงดันไฟฟ้าอินพุต ${V_i}$ เมื่อไหร่, ${R_fI_s}= 1V$. สังเกตว่าแรงดันขาออก${V_0}$ กำลังมีไฟล์ negative signซึ่งบ่งชี้ว่ามีความแตกต่างของเฟส180 ⁰ระหว่างอินพุตและเอาต์พุต

AC และ DC เป็นคำศัพท์สองคำที่คุณพบบ่อยขณะศึกษาการไหลของประจุไฟฟ้า Alternating Current (AC)มีคุณสมบัติในการเปลี่ยนสถานะอย่างต่อเนื่อง ตัวอย่างเช่นถ้าเราพิจารณาคลื่นไซน์กระแสจะไหลไปในทิศทางเดียวสำหรับครึ่งรอบบวกและในทิศทางตรงกันข้ามสำหรับครึ่งรอบที่เป็นลบ ในทางกลับกัน,Direct Current (DC) ไหลไปในทิศทางเดียวเท่านั้น

วงจรอิเล็กทรอนิกส์ซึ่งผลิตสัญญาณ DC หรือสัญญาณ DC แบบพัลส์เมื่อสัญญาณ AC ถูกนำไปใช้เรียกว่าเป็น rectifier. ในบทนี้จะกล่าวถึงรายละเอียดเกี่ยวกับวงจรเรียงกระแสแบบออปแอมป์

ประเภทของวงจรเรียงกระแส

วงจรเรียงกระแสแบ่งออกเป็นสองประเภท: Half wave rectifier และ Full wave rectifier. ส่วนนี้จะกล่าวถึงรายละเอียดทั้งสองประเภทนี้

วงจรเรียงกระแสครึ่งคลื่น

ก half wave rectifier เป็นวงจรเรียงกระแสที่สร้างครึ่งรอบบวกที่เอาต์พุตสำหรับหนึ่งรอบครึ่งหนึ่งของอินพุตและเอาต์พุตศูนย์สำหรับอีกครึ่งรอบของอินพุต

circuit diagram ของวงจรเรียงกระแสครึ่งคลื่นแสดงในรูปต่อไปนี้

สังเกตว่าแผนภาพวงจรของวงจรเรียงกระแสครึ่งคลื่นที่แสดงด้านบนดูเหมือนแอมพลิฟายเออร์แบบกลับหัวโดยมีไดโอด D ₁และ D _{2 สองตัว}อยู่ด้วย

working ของวงจรเรียงกระแสครึ่งคลื่นที่แสดงด้านบนได้อธิบายไว้ด้านล่าง

สำหรับ positive half cycleของอินพุตซายน์เอาต์พุตของ op-amp จะเป็นลบ ดังนั้นไดโอด D ₁จะเอนเอียงไปข้างหน้า
เมื่อไดโอด D ₁อยู่ในไบแอสไปข้างหน้าแรงดันเอาต์พุตของ op-amp จะเป็น -0.7 V. ดังนั้นไดโอด D ₂จะเอนเอียงแบบย้อนกลับ ดังนั้นoutput voltage ของวงจรข้างต้นคือ zero โวลต์
ดังนั้นจึงมี no (zero) output ของวงจรเรียงกระแสครึ่งคลื่นสำหรับครึ่งรอบบวกของอินพุตไซน์
สำหรับ negative half cycleของอินพุตรูปซายน์เอาต์พุตของ op-amp จะเป็นบวก ดังนั้นไดโอด D ₁และ D ₂จะเอนเอียงย้อนกลับและเอนเอียงไปข้างหน้าตามลำดับ ดังนั้นแรงดันขาออกของวงจรด้านบนจะเป็น -

$$V_0=-\left(\frac{R_f}{R_1}\right)V_1$$

ดังนั้นผลลัพธ์ของวงจรเรียงกระแสครึ่งคลื่นจะเป็น a positive half cycle สำหรับครึ่งรอบที่เป็นลบของอินพุตไซน์

รูปคลื่น

input และ output waveforms ของวงจรเรียงกระแสครึ่งคลื่นแสดงในรูปต่อไปนี้

ดังที่คุณเห็นจากกราฟด้านบนแผนภาพวงจรเรียงกระแสครึ่งคลื่นที่เรากล่าวถึงจะสร้างขึ้น positive half cycles สำหรับครึ่งรอบที่เป็นลบของอินพุตไซน์และเอาต์พุตศูนย์สำหรับครึ่งรอบที่เป็นบวกของอินพุตไซน์

วงจรเรียงกระแสแบบเต็มคลื่น

ก full wave rectifier สร้างครึ่งรอบบวกที่เอาต์พุตสำหรับทั้งครึ่งรอบของอินพุต

circuit diagram ของวงจรเรียงกระแสคลื่นเต็มแสดงในรูปต่อไปนี้ -

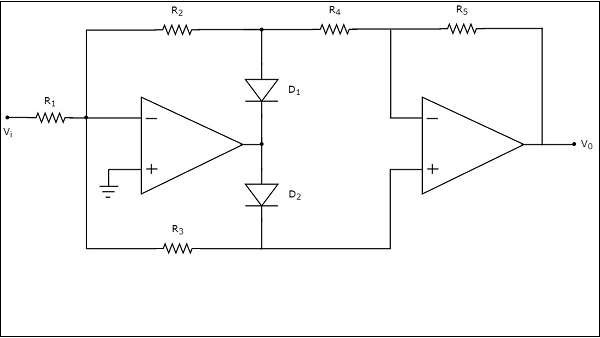
แผนภาพวงจรข้างต้นประกอบด้วยสองสหกรณ์แอมป์สองไดโอด, D ₁ & D ₂และห้าต้านทาน, R ₁จะ R 5working ของวงจรเรียงกระแสคลื่นเต็มที่แสดงด้านบนอธิบายไว้ด้านล่าง -

สำหรับ positive half cycleของอินพุตรูปซายน์เอาต์พุตของ op-amp ตัวแรกจะเป็นลบ ดังนั้นไดโอด D ₁และ D ₂จะเอนเอียงไปข้างหน้าและเอนเอียงย้อนกลับตามลำดับ
จากนั้นแรงดันไฟฟ้าขาออกของ op-amp ตัวแรกจะเป็น -

$$V_{01}=-\left(\frac{R_2}{R_1}\right)V_i$$

สังเกตว่าเอาต์พุตของ op-amp ตัวแรกเชื่อมต่อกับตัวต้านทาน R ₄ซึ่งเชื่อมต่อกับขั้วกลับด้านของ op-amp ตัวที่สอง แรงดันไฟฟ้าที่มีอยู่ที่ขั้วที่ไม่กลับด้านของ op-amp ตัวที่สองคือ 0 V ดังนั้น op-amp ตัวที่สองที่มีตัวต้านทาน R ₄และ R ₄ทำหน้าที่เป็นinverting amplifier.
แรงดันเอาต์พุตของ op-amp ตัวที่สองจะเป็น

$$V_0=-\left(\frac{R_5}{R_4}\right)V_{01}$$

Substituting คุณค่าของ $V_{01}$ ในสมการข้างต้นเราได้ -

$$=>V_{0}=-\left(\frac{R_5}{R_4}\right)\left \{ -\left(\frac{R_2}{R_1}\right)V_{i} \right \}$$

$$=>V_{0}=\left(\frac{R_2R_5}{R_1R_4}\right)V_{i}$$
ดังนั้นผลลัพธ์ของวงจรเรียงกระแสคลื่นเต็มจะเป็นครึ่งรอบบวกสำหรับ positive half cycleของอินพุตรูปซายน์ ในกรณีนี้กำไรของเอาต์พุตคือ$\frac{R_2R_5}{R_1R_4}$. หากเราพิจารณา$R_{1}=R_{2}=R_{4}=R_{5}=R$จากนั้นกำไรของเอาต์พุตจะเป็นหนึ่ง
สำหรับ negative half cycleของอินพุตรูปซายน์เอาต์พุตของ op-amp ตัวแรกจะเป็นบวก ดังนั้นไดโอด D ₁และ D ₂จะเอนเอียงย้อนกลับและเอนเอียงไปข้างหน้าตามลำดับ
แรงดันเอาต์พุตของ op-amp ตัวแรกจะเป็น -

$$V_{01}=-\left(\frac{R_3}{R_1}\right)V_{i}$$

เอาต์พุตของ op-amp ตัวแรกเชื่อมต่อโดยตรงกับเทอร์มินัลที่ไม่กลับด้านของ op-amp ตัวที่สอง ตอนนี้ออปแอมป์ตัวที่สองพร้อมตัวต้านทาน R ₄และ R ₅ทำหน้าที่เป็นnon-inverting amplifier.

แรงดันไฟฟ้าขาออกของ op-amp ตัวที่สองจะเป็น -

$$V_{0}=\left(1+\frac{R_5}{R_4}\right)V_{01}$$

Substituting คุณค่าของ $V_{01}$ ในสมการข้างต้นเราได้

$$=>V_{0}=\left(1+\frac{R_5}{R_4}\right) \left\{-\left(\frac{R_3}{R_1}\right)V_{i}\right \} $$

$$=>V_{0}=-\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)V_{i}$$
ดังนั้นผลลัพธ์ของวงจรเรียงกระแสคลื่นเต็มจะเป็น a positive half cycleสำหรับครึ่งรอบเชิงลบของอินพุตไซน์ด้วย ในกรณีนี้ขนาดของอัตราขยายของเอาต์พุตคือ$\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)$. หากเราพิจารณา$R_{1}=2R_{3}=R_{4}=R_{5}=R$ จากนั้นกำไรของผลลัพธ์จะเป็น one.

input และ output waveforms ของวงจรเรียงกระแสแบบเต็มคลื่นจะแสดงในรูปต่อไปนี้

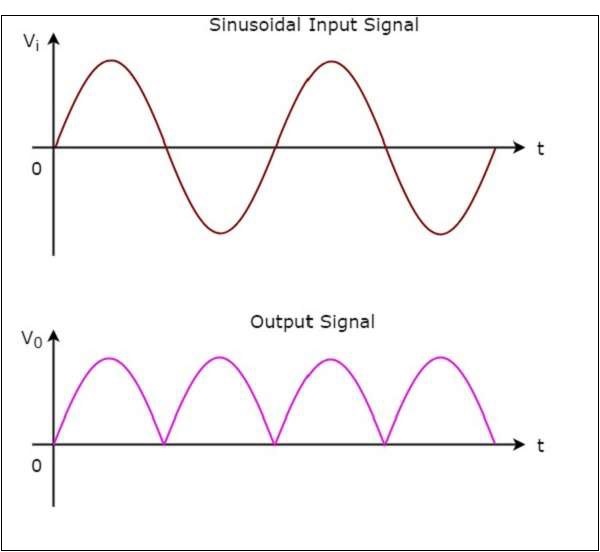
ดังที่คุณเห็นในรูปด้านบนแผนภาพวงจรเรียงกระแสคลื่นเต็มรูปแบบที่เราพิจารณาจะสร้างขึ้นเท่านั้น positive half cycles สำหรับทั้งครึ่งรอบบวกและลบของอินพุตไซน์

Wave shaping circuitsคือวงจรอิเล็กทรอนิกส์ซึ่งสร้างรูปร่างที่ต้องการที่เอาต์พุตจากรูปคลื่นอินพุตที่ใช้ วงจรเหล่านี้ทำหน้าที่สองอย่าง -

ลดคลื่นที่ใช้
เปลี่ยนระดับ dc ของคลื่นที่ใช้

วงจรสร้างคลื่นมีสองประเภท: Clippers และ Clampers. ในบทนี้คุณจะได้เรียนรู้รายละเอียดเกี่ยวกับปัตตาเลี่ยน

ปัตตาเลี่ยนที่ใช้ Op-amp

ก clipperเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตโดยการลบส่วนหนึ่งของอินพุตด้านบนหรือด้านล่างค่าอ้างอิง นั่นหมายความว่าเอาต์พุตของปัตตาเลี่ยนจะเหมือนกับอินพุตสำหรับส่วนอื่นที่ไม่ใช่ส่วนที่ถูกตัดออก ด้วยเหตุนี้แอมพลิจูดสูงสุดถึงจุดสูงสุดของเอาต์พุตของปัตตาเลี่ยนจะน้อยกว่าอินพุตเสมอ

ข้อได้เปรียบหลักของปัตตาเลี่ยนคือการกำจัดสัญญาณรบกวนที่ไม่ต้องการที่มีอยู่ในแอมพลิจูดของสัญญาณ ac

ปัตตาเลี่ยนสามารถแบ่งออกเป็นสองประเภทดังต่อไปนี้โดยพิจารณาจากส่วนการตัดของอินพุต

คลิปเปอร์บวก
Clipper เชิงลบ

สิ่งเหล่านี้จะกล่าวถึงในรายละเอียดตามที่ระบุด้านล่าง -

คลิปเปอร์บวก

ก positive clipper เป็นปัตตาเลี่ยนที่คลิปเฉพาะส่วนบวกของสัญญาณอินพุต

circuit diagramของปัตตาเลี่ยนที่เป็นบวกจะแสดงในรูปต่อไปนี้ -

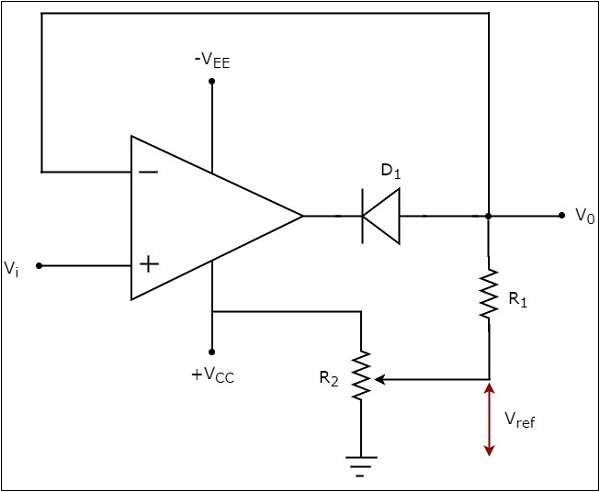
ในวงจรที่แสดงด้านบนสัญญาณแรงดันไฟฟ้ารูปไซน์ $V_{t}$ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านของ op-amp ค่าของแรงดันอ้างอิง$V_{ref}$ สามารถเลือกได้โดยการเปลี่ยนค่าตัวต้านทาน $R_{2}$.

operation ของวงจรที่แสดงด้านบนอธิบายไว้ด้านล่าง -

ถ้าค่าของแรงดันไฟฟ้าขาเข้า $V_i$ น้อยกว่าค่าของแรงดันอ้างอิง $V_{ref}$จากนั้นไดโอด D _{1 จะ}ดำเนินการ จากนั้นวงจรที่ให้ไว้ข้างต้นจะทำงานเป็นvoltage follower. ดังนั้นแรงดันขาออก$V_{0}$ ของวงจรข้างต้นจะเหมือนกับแรงดันไฟฟ้าขาเข้า $V_{i}$สำหรับ $V_{i}$ < $V_{ref}$.
ถ้าค่าของแรงดันไฟฟ้าขาเข้า $V_{i}$ มากกว่าค่าของแรงดันอ้างอิง $V_{ref}$จากนั้นไดโอด D ₁จะดับลง ตอนนี้ op-amp ทำงานในวงเปิดเนื่องจากเส้นทางข้อเสนอแนะเปิดอยู่ ดังนั้นแรงดันขาออก$V_{0}$ ของวงจรข้างต้นจะเท่ากับค่าของแรงดันไฟฟ้าอ้างอิง $V_{ref}$สำหรับ $V_{i}$ > $V_{ref}$.

input wave form และที่เกี่ยวข้อง output wave form ของปัตตาเลี่ยนบวกสำหรับแรงดันอ้างอิงที่เป็นบวก $V_{ref}$แสดงในรูปต่อไปนี้ -

Clipper เชิงลบ

ก negative clipperเป็นปัตตาเลี่ยนที่คลิปเฉพาะส่วนลบของสัญญาณอินพุต คุณสามารถรับวงจรของปัตตาเลี่ยนลบได้เพียงแค่กลับไดโอดและใช้ขั้วย้อนกลับของแรงดันอ้างอิงในวงจรที่คุณเห็นสำหรับปัตตาเลี่ยนบวก

circuit diagram ของปัตตาเลี่ยนลบจะแสดงในรูปต่อไปนี้ -

ในวงจรข้างต้นสัญญาณแรงดันไฟฟ้ารูปซายน์ $V_{i}$ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านของ op-amp ค่าของแรงดันอ้างอิง$V_{ref}$ สามารถเลือกได้โดยการเปลี่ยนค่าตัวต้านทาน $R_{2}$.

operation ของวงจร clipper ลบอธิบายไว้ด้านล่าง -

ถ้าค่าของแรงดันไฟฟ้าขาเข้า $V_{t}$ มากกว่าค่าของแรงดันอ้างอิง $V_{ref}$จากนั้นไดโอด D _{1 จะ}ดำเนินการ จากนั้นวงจรข้างต้นจะทำงานเป็นvoltage follower. ดังนั้นแรงดันขาออก$V_{0}$ ของวงจรข้างต้นจะเหมือนกับแรงดันไฟฟ้าขาเข้า $V_{i}$ สำหรับ $V_{i}$> $V_{ref}$.

ถ้าค่าของแรงดันไฟฟ้าขาเข้า $V_{i}$น้อยกว่าค่าของแรงดันอ้างอิงจากนั้นไดโอด D ₁จะดับลง ตอนนี้ op-amp ทำงานในวงเปิดเนื่องจากเส้นทางข้อเสนอแนะเปิดอยู่ ดังนั้นแรงดันขาออก$V_{0}$ ของวงจรข้างต้นจะเท่ากับค่าของแรงดันอ้างอิง$V_{ref}$ สำหรับ $V_{i}$ < $V_{ref}$.

input wave form และที่เกี่ยวข้อง output wave form ของปัตตาเลี่ยนลบสำหรับแรงดันอ้างอิงเชิงลบ $V_{ref}$แสดงในรูปต่อไปนี้ -

ในบทที่แล้วเราได้กล่าวถึงปัตตาเลี่ยน ตอนนี้ให้เราพูดคุยเกี่ยวกับวงจรการสร้างคลื่นประเภทอื่นคือแคลมป์เกอร์

แคลมป์ที่ใช้ Op-amp

ก clamperเป็นวงจรอิเล็กทรอนิกส์ที่สร้างเอาต์พุตซึ่งคล้ายกับอินพุต แต่มีการเลื่อนระดับ DC กล่าวอีกนัยหนึ่งเอาต์พุตของ clamper เป็นแบบจำลองที่แน่นอนของอินพุต ดังนั้นแอมพลิจูดสูงสุดถึงพีคของเอาต์พุตของ clamper จะเท่ากับของอินพุตเสมอ

แคลมป์เกอร์ใช้เพื่อแนะนำหรือเรียกคืนระดับ DC ของสัญญาณอินพุตที่เอาต์พุต มีtwo types ของแคลมป์ที่ใช้ op-amp ตามการเปลี่ยน DC ของอินพุต

Clamper บวก
Clamper เชิงลบ

ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับแคลมป์เกอร์ทั้งสองประเภทนี้

Clamper บวก

Clamper บวกคือวงจร clamper ที่สร้างเอาต์พุตในลักษณะที่สัญญาณอินพุตถูกเลื่อนในแนวตั้งโดยค่า DC ที่เป็นบวก

circuit diagram ของ clamper ที่เป็นบวกแสดงในรูปต่อไปนี้ -

ในวงจรข้างต้น a sinusoidal voltage signal, $V_{i}$ ถูกนำไปใช้กับขั้วกลับด้านของ op-amp ผ่านเครือข่ายที่ประกอบด้วยตัวเก็บประจุ $C_{1}$ และตัวต้านทาน $R_{1}$. นั่นหมายความว่าสัญญาณแรงดันไฟฟ้ากระแสสลับจะถูกนำไปใช้กับขั้วกลับด้านของ op-amp

DC reference voltage $V_{ref}$ ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านของ op-amp ค่าของแรงดันอ้างอิง$V_{ref}$ สามารถเลือกได้โดยการเปลี่ยนค่าตัวต้านทาน $R_{2}$. ในกรณีนี้เราจะได้รับแรงดันไฟฟ้าอ้างอิง$V_{ref}$ ของค่าบวก

วงจรข้างต้นสร้างไฟล์ output, ที่ is the combination (resultant sum) ของสัญญาณแรงดันไฟฟ้ารูปไซน์ $V_{i}$ และแรงดันไฟฟ้าอ้างอิง $V_{ref}$. นั่นหมายความว่าวงจร clamper จะสร้างเอาต์พุตในลักษณะที่สัญญาณแรงดันไฟฟ้าไซน์$V_{i}$ ได้รับการเลื่อนในแนวตั้งขึ้นตามค่าของแรงดันอ้างอิง $V_{ref}$.

รูปคลื่นอินพุตและรูปคลื่นเอาต์พุตที่สอดคล้องกันของครีเอทีฟบวกแสดงไว้ในรูปด้านบน -

จากรูปด้านบนคุณสามารถสังเกตได้ว่าตัวหนีบบวกจะเปลี่ยนรูปคลื่นอินพุตที่ใช้ vertically upwardที่เอาต์พุต จำนวนกะจะขึ้นอยู่กับค่าของแรงดันไฟฟ้าอ้างอิง DC

Clamper เชิงลบ

ก negative clamper เป็นวงจร clamper ที่สร้างเอาต์พุตในลักษณะที่สัญญาณอินพุตถูกเลื่อนในแนวตั้งโดยค่า DC เชิงลบ

circuit diagram ของ clamper เชิงลบแสดงในรูปต่อไปนี้ -

ในวงจรข้างต้น a sinusoidal voltage signal $V_{i}$ ถูกนำไปใช้กับขั้วกลับด้านของ op-amp ผ่านเครือข่ายที่ประกอบด้วยตัวเก็บประจุ C ₁และตัวต้านทาน$R_{1}$. นั่นหมายความว่าสัญญาณแรงดันไฟฟ้ากระแสสลับจะถูกนำไปใช้กับขั้วกลับด้านของ op-amp

DC reference voltage $V_{ref}$ ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านของ op-amp ค่าของแรงดันอ้างอิง $V_{ref}$ สามารถเลือกได้โดยการเปลี่ยนค่าตัวต้านทาน $R_{2}$. ในกรณีนี้เราจะได้รับแรงดันไฟฟ้าอ้างอิง$V_{ref}$ ของค่าลบ

วงจรด้านบนสร้างเอาต์พุตซึ่งเป็นการรวมกัน (ผลรวมผลลัพธ์) ของสัญญาณแรงดันไฟฟ้ารูปไซน์ $V_{i}$ และแรงดันไฟฟ้าอ้างอิง $V_{ref}$. นั่นหมายความว่าวงจร clamper จะสร้างเอาต์พุตในลักษณะที่สัญญาณแรงดันไฟฟ้าไซน์$V_{i}$ ได้รับการเลื่อนลงในแนวตั้งตามค่าของแรงดันไฟฟ้าอ้างอิง $V_{ref}$.

รูปคลื่นอินพุตและรูปคลื่นเอาท์พุตที่สอดคล้องกันของแคลมเปอร์ลบจะแสดงในรูปต่อไปนี้ -

เราสามารถสังเกตได้จากเอาต์พุตที่แคลมเปอร์ลบจะเปลี่ยนรูปคลื่นอินพุตที่ใช้ vertically downwardที่เอาต์พุต ปริมาณการขยับจะขึ้นอยู่กับค่าของแรงดันไฟฟ้าอ้างอิง DC

Filtersเป็นวงจรอิเล็กทรอนิกส์ที่อนุญาตให้ใช้ส่วนประกอบความถี่บางอย่างและ / หรือปฏิเสธอื่น ๆ คุณอาจเจอตัวกรองในบทช่วยสอนทฤษฎีเครือข่าย พวกมันเป็นแบบพาสซีฟและเป็นวงจรไฟฟ้าหรือเครือข่ายที่ประกอบด้วยองค์ประกอบแฝงเช่นตัวต้านทานตัวเก็บประจุและ (หรือ) ตัวเหนี่ยวนำ

ในบทนี้จะกล่าวถึง active filters ในรายละเอียด.

ประเภทของตัวกรองที่ใช้งานอยู่

ตัวกรองที่ใช้งานคือวงจรอิเล็กทรอนิกส์ซึ่งประกอบด้วยองค์ประกอบที่ใช้งานอยู่เช่น op-amp (s) พร้อมกับองค์ประกอบแฝงเช่นตัวต้านทานและตัวเก็บประจุ

ตัวกรองที่ใช้งานส่วนใหญ่แบ่งออกเป็นดังต่อไปนี้ four types ตามย่านความถี่ที่อนุญาตและ / หรือปฏิเสธ -

ตัวกรองความถี่ต่ำที่ใช้งานอยู่
ตัวกรองความถี่สูงที่ใช้งานอยู่
ตัวกรอง Active Band Pass
ตัวกรอง Active Band Stop

ตัวกรองความถี่ต่ำที่ใช้งานอยู่

หากตัวกรองที่ใช้งานอยู่อนุญาต (ผ่าน) เท่านั้น low frequency ส่วนประกอบและปฏิเสธ (บล็อก) ส่วนประกอบความถี่สูงอื่น ๆ ทั้งหมดจากนั้นจะเรียกว่าเป็น active low pass filter.

circuit diagram ของตัวกรองความถี่ต่ำที่ใช้งานอยู่จะแสดงในรูปต่อไปนี้ -

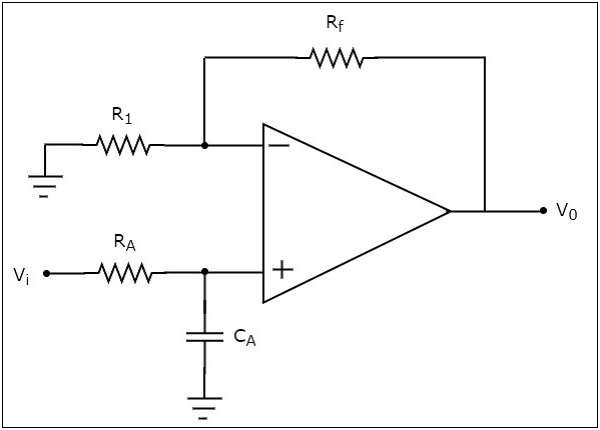
เรารู้ว่าเครือข่ายไฟฟ้าซึ่งเชื่อมต่อกับเทอร์มินัลที่ไม่กลับด้านของ op-amp คือ a passive low pass filter. ดังนั้นอินพุตของเทอร์มินัลที่ไม่กลับด้านของ opamp คือเอาต์พุตของตัวกรองความถี่ต่ำแบบพาสซีฟ

สังเกตว่าวงจรด้านบนคล้ายกับ non-inverting amplifier. มีเอาต์พุตของตัวกรองความถี่ต่ำแบบพาสซีฟเป็นอินพุตไปยังเทอร์มินัลที่ไม่กลับด้านของ op-amp ดังนั้นจึงสร้างผลลัพธ์ซึ่งก็คือ$\left(1+\frac{R_f}{R_1}\right)$ เท่าของอินพุตที่มีอยู่ที่เทอร์มินัลที่ไม่กลับด้าน

เราสามารถเลือกค่าของ $R_{f}$ และ $R_{1}$ อย่างเหมาะสมเพื่อให้ได้มาซึ่ง desired gainที่เอาต์พุต สมมติว่าถ้าเราพิจารณาค่าความต้านทานของ$R_{f}$ และ $R_{1}$ เป็นศูนย์โอห์มและอินฟินิตี้โอห์มจากนั้นวงจรด้านบนจะสร้าง a unity gain เอาต์พุตตัวกรองความถี่ต่ำ

ตัวกรองความถี่สูงที่ใช้งานอยู่

หากตัวกรองที่ใช้งานอยู่อนุญาต (ผ่าน) เท่านั้น high frequency ส่วนประกอบและปฏิเสธ (บล็อก) ส่วนประกอบความถี่ต่ำอื่น ๆ ทั้งหมดจึงเรียกว่า active high pass filter.

circuit diagram ของตัวกรองความถี่สูงที่ใช้งานอยู่จะแสดงในรูปต่อไปนี้ -

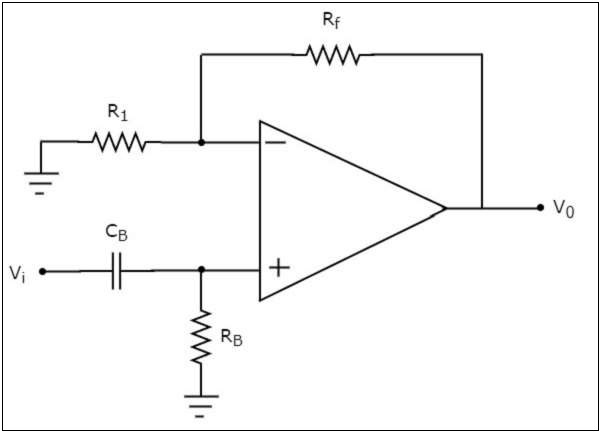
เรารู้ว่าเครือข่ายไฟฟ้าซึ่งเชื่อมต่อกับเทอร์มินัลที่ไม่กลับด้านของ op-amp คือ a passive high pass filter. ดังนั้นอินพุตของเทอร์มินัลที่ไม่กลับด้านของ opamp คือเอาต์พุตของตัวกรองความถี่สูงแบบพาสซีฟ

ตอนนี้วงจรด้านบนคล้ายกับ non-inverting amplifier. มีเอาต์พุตของตัวกรองความถี่สูงแบบพาสซีฟเป็นอินพุตไปยังเทอร์มินัลที่ไม่กลับด้านของ op-amp ดังนั้นจึงสร้างผลลัพธ์ซึ่งก็คือ$\left(1+\frac{R_f}{R_1}\right)$ ครั้งที่อินพุตปรากฏที่เทอร์มินัลที่ไม่กลับด้าน

เราสามารถเลือกค่าของ $R_f$ และ $R_1$ อย่างเหมาะสมเพื่อให้ได้มาซึ่ง desired gainที่เอาต์พุต สมมติว่าถ้าเราพิจารณาค่าความต้านทานของ$R_{f}$ และ $R_{1}$ เป็นศูนย์โอห์มและอินฟินิตี้โอห์มจากนั้นวงจรด้านบนจะสร้าง a unity gain เอาต์พุตตัวกรองความถี่สูง

ตัวกรอง Active Band Pass

หากตัวกรองที่ใช้งานอยู่อนุญาตให้ (ส่งผ่าน) ย่านความถี่เดียวเท่านั้นจะเรียกว่าเป็น active band pass filter. โดยทั่วไปแถบความถี่นี้จะอยู่ระหว่างช่วงความถี่ต่ำและช่วงความถี่สูง ดังนั้นตัวกรองคลื่นความถี่แอคทีฟแบนด์จะปฏิเสธ (บล็อก) ทั้งส่วนประกอบความถี่ต่ำและสูง

circuit diagram ของตัวกรองคลื่นความถี่ที่ใช้งานอยู่จะแสดงในรูปต่อไปนี้

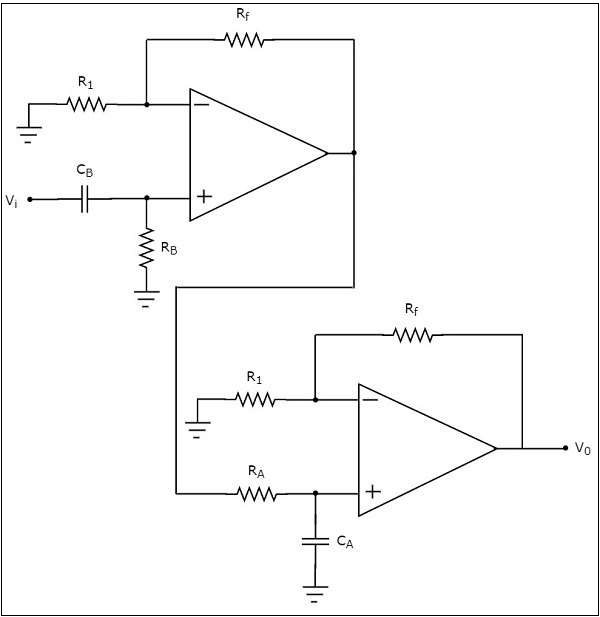
สังเกตว่ามี two parts ในแผนภาพวงจรของแอคทีฟแบนด์พาสฟิลเตอร์: ส่วนแรกคือตัวกรองความถี่สูงที่ใช้งานอยู่ในขณะที่ส่วนที่สองเป็นตัวกรองความถี่ต่ำที่ใช้งานอยู่

เอาต์พุตของตัวกรองความถี่สูงที่ใช้งานอยู่ถูกนำไปใช้เป็นอินพุตของตัวกรองความถี่ต่ำที่ใช้งานอยู่นั่นหมายความว่าทั้งตัวกรองความถี่สูงที่ใช้งานอยู่และตัวกรองความถี่ต่ำที่ใช้งานอยู่ cascaded เพื่อให้ได้เอาต์พุตในลักษณะที่มีเฉพาะย่านความถี่เฉพาะ

active high pass filterซึ่งมีอยู่ในขั้นแรกอนุญาตให้ความถี่ที่มากกว่า lower cut-off frequencyของตัวกรองคลื่นความถี่ที่ใช้งานอยู่ ดังนั้นเราต้องเลือกค่าของ$R_{B}$ และ $C_{B}$ อย่างเหมาะสมเพื่อให้ได้มาซึ่งสิ่งที่ต้องการ lower cut-off frequency ของตัวกรองคลื่นความถี่ที่ใช้งานอยู่

ในทำนองเดียวกัน active low pass filterซึ่งมีอยู่ในขั้นตอนที่สองทำให้ความถี่ที่มีขนาดเล็กกว่าความถี่ตัดที่สูงกว่าของตัวกรองสัญญาณความถี่ที่ใช้งานอยู่ ดังนั้นเราต้องเลือกค่าของ$R_{A}$ และ $C_{A}$ อย่างเหมาะสมเพื่อให้ได้มาซึ่งสิ่งที่ต้องการ higher cut-off frequency ของตัวกรองคลื่นความถี่ที่ใช้งานอยู่

ดังนั้นวงจรในแผนภาพที่กล่าวถึงข้างต้นจะสร้างเอาต์พุตตัวกรองสัญญาณความถี่ที่ใช้งานอยู่

ตัวกรอง Active Band Stop

หากตัวกรองที่ใช้งานอยู่ปฏิเสธ (บล็อก) ย่านความถี่หนึ่ง ๆ จะเรียกว่าเป็น active band stop filter. โดยทั่วไปแถบความถี่นี้จะอยู่ระหว่างช่วงความถี่ต่ำและช่วงความถี่สูง ดังนั้นตัวกรองหยุดแบนด์ที่ใช้งานอยู่จึงอนุญาต (ส่งผ่าน) ทั้งส่วนประกอบความถี่ต่ำและสูง

block diagram ของฟิลเตอร์หยุดแบนด์ที่ใช้งานอยู่จะแสดงในรูปต่อไปนี้ -

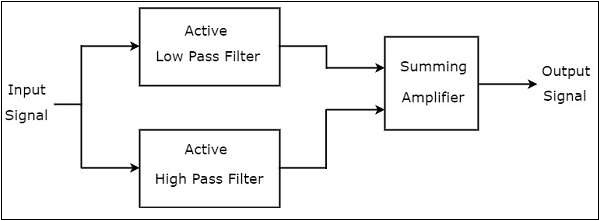
สังเกตว่าบล็อกไดอะแกรมของตัวกรองหยุดแบนด์ที่ใช้งานอยู่ประกอบด้วยสองช่วงตึกในขั้นตอนแรก: ตัวกรองความถี่ต่ำที่ใช้งานอยู่และตัวกรองความถี่สูงที่ใช้งานอยู่ เอาต์พุตของสองบล็อกนี้ถูกนำไปใช้เป็นอินพุตไปยังบล็อกที่มีอยู่ในขั้นตอนที่สอง ดังนั้นsumming amplifier สร้างเอาต์พุตซึ่งเป็นเวอร์ชันขยายของผลรวมของเอาต์พุตของตัวกรองความถี่ต่ำที่ใช้งานอยู่และตัวกรองความถี่สูงที่ใช้งานอยู่

ดังนั้นผลลัพธ์ของแผนภาพบล็อกด้านบนจะเป็นไฟล์ output of an active band stop เมื่อเราเลือกความถี่ตัดของตัวกรองความถี่ต่ำให้เล็กกว่าความถี่ตัดของตัวกรองความถี่สูง

circuit diagram ของฟิลเตอร์หยุดแบนด์ที่ใช้งานอยู่จะแสดงในรูปต่อไปนี้ -

เราได้เห็นแผนภาพวงจรของตัวกรองความถี่ต่ำที่ใช้งานอยู่ตัวกรองความถี่สูงที่ใช้งานอยู่และเครื่องขยายเสียงรวม สังเกตว่าเราได้รับข้างต้นcircuit diagram ของตัวกรองหยุดแบนด์ที่ใช้งานอยู่โดยแทนที่บล็อกด้วยแผนภาพวงจรตามลำดับในแผนภาพบล็อกของตัวกรองหยุดแบนด์ที่ใช้งานอยู่

ออสซิลเลเตอร์เป็นวงจรอิเล็กทรอนิกส์ที่สร้างสัญญาณเป็นระยะ ถ้าออสซิลเลเตอร์สร้างการสั่นแบบไซน์เรียกว่า asinusoidal oscillator. จะแปลงพลังงานอินพุตจากแหล่ง DC เป็นพลังงานเอาท์พุต AC ของสัญญาณเป็นระยะ สัญญาณระยะนี้จะมีความถี่และแอมพลิจูดเฉพาะ

block diagram ของออสซิลเลเตอร์ซายน์แสดงในรูปต่อไปนี้ -

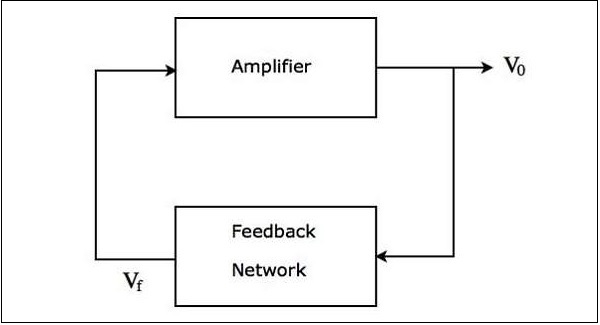
รูปด้านบนส่วนใหญ่ประกอบด้วย two blocks: เครื่องขยายเสียงและเครือข่ายป้อนกลับเครือข่ายป้อนกลับใช้ส่วนหนึ่งของเอาต์พุตของเครื่องขยายเสียงเป็นอินพุตและสร้างสัญญาณแรงดันไฟฟ้า สัญญาณแรงดันไฟฟ้านี้ใช้เป็นอินพุตไปยังเครื่องขยายเสียง

แผนภาพบล็อกของ oscillator ไซน์ที่แสดงด้านบนสร้างการสั่นของไซน์เมื่อต่อไปนี้ two conditions พอใจ -

loop gain $A_{v}\beta$ ของแผนภาพบล็อกข้างต้นของ oscillator ไซน์ต้องมากกว่าหรือเท่ากับ unity. ที่นี่$A_{v}$ และ $\beta$ คือการเพิ่มของแอมพลิฟายเออร์และกำไรของเครือข่ายป้อนกลับตามลำดับ
ผลรวม phase shift รอบ ๆ ห่วงของแผนภาพบล็อกด้านบนของ oscillator ไซน์ต้องเป็นอย่างใดอย่างหนึ่ง 0⁰ หรือ 360⁰.

สองเงื่อนไขข้างต้นรวมกันเรียกว่า Barkhausen criteria.

ออสซิลเลเตอร์ที่ใช้ Op-Amp

มี two ประเภทของออสซิลเลเตอร์ที่ใช้ op-amp

ออสซิลเลเตอร์กะระยะ RC
ออสซิลเลเตอร์สะพาน Wien

ส่วนนี้จะกล่าวถึงแต่ละข้อโดยละเอียด

RC Phase Shift Oscillator

ออสซิลเลเตอร์ที่ใช้ op-amp ซึ่งสร้างสัญญาณแรงดันไฟฟ้าไซน์ที่เอาต์พุตด้วยความช่วยเหลือของแอมพลิฟายเออร์กลับด้านและเครือข่ายป้อนกลับเรียกว่า a RC phase shift oscillator. เครือข่ายข้อเสนอแนะนี้ประกอบด้วยส่วน RC แบบเรียงซ้อนสามส่วน

circuit diagram ของออสซิลเลเตอร์กะระยะ RC แสดงในรูปต่อไปนี้ -

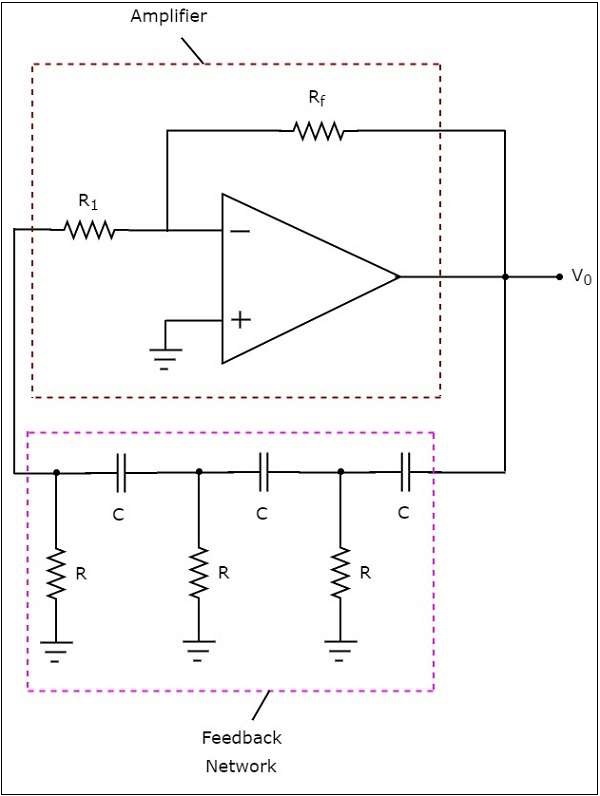
ในวงจรด้านบน op-amp ทำงานอยู่ inverting mode. ดังนั้นจึงมีการเปลี่ยนเฟส 180 0ปัจจุบันเครือข่ายข้อเสนอแนะในวงจรดังกล่าวข้างต้นนอกจากนี้ยังมีการเปลี่ยนเฟส 180 ⁰เนื่องจากแต่ละส่วน RC ให้กะระยะ 60 0ดังนั้นวงจรข้างต้นจึงให้การกะระยะทั้งหมดที่ 360 ⁰ที่ความถี่บางช่วง

output frequency ของออสซิลเลเตอร์กะระยะ RC คือ -

$$f=\frac{1}{2\Pi RC\sqrt[]{6}}$$

gain $A_{v}$ ของแอมพลิฟายเออร์แบบกลับด้านควรมากกว่าหรือเท่ากับ -29

$$i.e.,-\frac{R_f}{R_1}\geq-29$$

$$=>\frac{R_f}{R_1}\geq-29$$

$$=>R_{f}\geq29R_{1}$$

ดังนั้นเราควรพิจารณาค่าของตัวต้านทานแบบป้อนกลับ $R_{f}$อย่างน้อย 29 เท่าของค่าตัวต้านทาน $R_{1}$เพื่อสร้างการสั่นอย่างต่อเนื่องที่เอาต์พุตของ RC phase shift oscillator

Wien Bridge Oscillator

ออสซิลเลเตอร์ที่ใช้ op-amp ซึ่งสร้างสัญญาณแรงดันไฟฟ้ารูปไซน์ที่เอาต์พุตด้วยความช่วยเหลือของเครื่องขยายเสียงที่ไม่กลับด้านและเครือข่ายป้อนกลับเรียกว่า Wien bridge oscillator.

circuit diagram ของออสซิลเลเตอร์สะพาน Wien แสดงในรูปต่อไปนี้ -

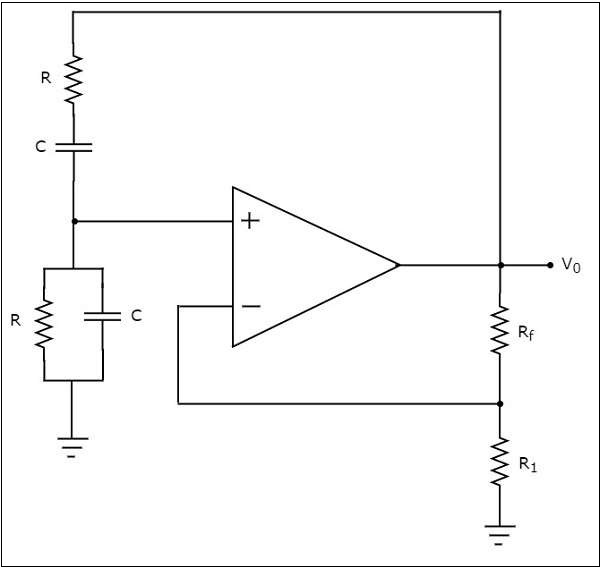
ในวงจรที่แสดงด้านบนสำหรับ Wein bridge oscillator op-amp ทำงานอยู่ non inverting mode. ดังนั้นจึงมีการเปลี่ยนเฟสเป็น 00 ดังนั้นเครือข่ายป้อนกลับที่อยู่ในวงจรข้างต้นไม่ควรมีการเลื่อนเฟสใด ๆ

หากเครือข่ายข้อเสนอแนะมีการเลื่อนเฟสเราต้องทำ balance the bridgeในลักษณะที่ไม่ควรมีการเลื่อนเฟสใด ๆ ดังนั้นวงจรข้างต้นจึงให้การเปลี่ยนเฟสทั้งหมดเป็น 0 ⁰ที่ความถี่บางช่วง

output frequency ของ Wien bridge oscillator คือ

$$f=\frac{1}{2\Pi RC}$$

gain $A_{v}$ ของแอมพลิฟายเออร์ที่ไม่กลับด้านควรมากกว่าหรือเท่ากับ 3

$$i.e.,1+\frac{R_f}{R_1}\geq3$$

$$=>\frac{R_f}{R_1}\geq2$$

$$=>R_{f}\geq2R_{1}$$

ดังนั้นเราควรพิจารณาค่าของตัวต้านทานแบบป้อนกลับ $R_{f}$ อย่างน้อยสองเท่าของค่าตัวต้านทาน $R_{1}$ เพื่อสร้างการสั่นอย่างต่อเนื่องที่เอาต์พุตของ Wien bridge oscillator

ก waveform generatorเป็นวงจรอิเล็กทรอนิกส์ซึ่งสร้างคลื่นมาตรฐาน เครื่องกำเนิดรูปคลื่นที่ใช้ op-amp มีสองประเภท -

เครื่องกำเนิดคลื่นสี่เหลี่ยม
เครื่องกำเนิดคลื่นสามเหลี่ยม

บทนี้จะกล่าวถึงรายละเอียดของเครื่องกำเนิดรูปคลื่นที่ใช้ op-amp เหล่านี้

เครื่องกำเนิดคลื่นสี่เหลี่ยม

ก square wave generatorเป็นวงจรอิเล็กทรอนิกส์ที่สร้างคลื่นสี่เหลี่ยม ส่วนนี้จะกล่าวถึงเกี่ยวกับเครื่องกำเนิดคลื่นสี่เหลี่ยมที่ใช้ op-amp

circuit diagram ของเครื่องกำเนิดคลื่นสี่เหลี่ยมที่ใช้ op-amp จะแสดงในรูปต่อไปนี้

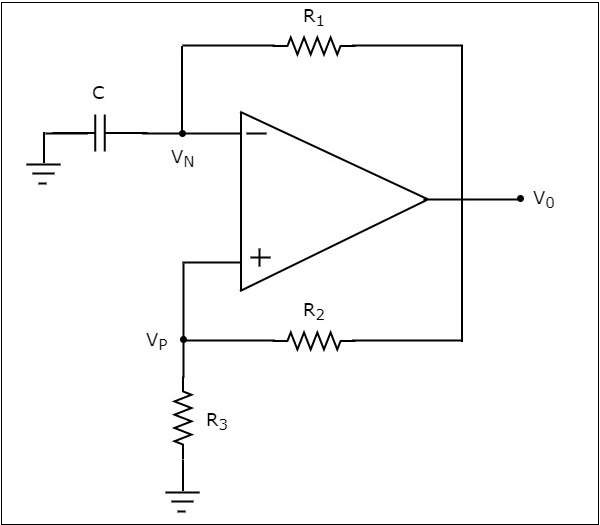
สังเกตว่าในแผนภาพวงจรที่แสดงด้านบนตัวต้านทาน $R_{1}$เชื่อมต่อระหว่างขั้วอินพุตกลับด้านของ op-amp และเอาต์พุตของ op-amp ดังนั้นตัวต้านทาน$R_{1}$ ใช้ในไฟล์ negative feedback. ในทำนองเดียวกันตัวต้านทาน$R_{2}$เชื่อมต่อระหว่างขั้วอินพุตที่ไม่เปลี่ยนทิศทางของ op-amp และเอาท์พุท ดังนั้นตัวต้านทาน$R_{2}$ ใช้ในไฟล์ positive feedback เส้นทาง.

ตัวเก็บประจุ C เชื่อมต่อระหว่างขั้วอินพุตกลับด้านของ op-amp และกราวด์ ดังนั้นvoltage across capacitor Cจะเป็นแรงดันไฟฟ้าขาเข้าที่ขั้วต่อกลับของ op-amp ในทำนองเดียวกันตัวต้านทาน$R_{3}$เชื่อมต่อระหว่างขั้วอินพุตที่ไม่กลับด้านของ op-amp และกราวด์ ดังนั้นvoltage across resistor $R_{3}$ จะเป็นแรงดันไฟฟ้าขาเข้าที่ขั้วที่ไม่กลับหัวของ op-amp

operation ของเครื่องกำเนิดคลื่นสี่เหลี่ยมมีคำอธิบายด้านล่าง -

สมมติว่ามี no chargeเก็บไว้ในตัวเก็บประจุในตอนแรก จากนั้นแรงดันไฟฟ้าที่มีอยู่ที่ขั้วกลับด้านของ op-amp เป็นศูนย์โวลต์ แต่มีแรงดันไฟฟ้าชดเชยที่ขั้วที่ไม่กลับหัวของ op-amp ด้วยเหตุนี้ค่าปัจจุบันที่เอาต์พุตของวงจรด้านบนจะเป็น$+V_{sat}$.
ตอนนี้ตัวเก็บประจุ C เริ่มทำงาน charging ผ่านตัวต้านทาน $R_{1}$. ค่าที่แสดงที่เอาต์พุตของวงจรข้างต้นจะเปลี่ยนเป็น$-V_{sat}$เมื่อแรงดันไฟฟ้าทั่วตัวเก็บประจุ C ถึงมากกว่าแรงดันไฟฟ้า (ค่าบวก) ข้ามตัวต้านทาน $R_{3}$.
ตัวเก็บประจุ C เริ่มทำงาน discharging ผ่านตัวต้านทาน $R_{1}$เมื่อเอาต์พุตของวงจรด้านบนคือ $-V_{sat}$. ค่าปัจจุบันที่เอาต์พุตของวงจรด้านบนจะเปลี่ยนเป็น$+V_{sat}$เมื่อแรงดันไฟฟ้าข้ามตัวเก็บประจุ C ถึงน้อยกว่า (ค่าลบมากกว่า) แรงดันไฟฟ้า (ค่าลบ) ข้ามตัวต้านทาน $R_{3}$.

ดังนั้นวงจรที่แสดงในแผนภาพด้านบนจะสร้างไฟล์ square wave ที่เอาต์พุตดังแสดงในรูปต่อไปนี้ -

จากรูปด้านบนเราสามารถสังเกตได้ว่าผลลัพธ์ของเครื่องกำเนิดคลื่นสี่เหลี่ยมจะมีหนึ่งในสองค่า: $+V_{sat}$ และ $-V_{sat}$. ดังนั้นผลลัพธ์จะยังคงอยู่ที่ค่าหนึ่งในช่วงเวลาหนึ่งจากนั้นจึงเปลี่ยนไปเป็นค่าอื่นและยังคงอยู่ที่นั่นในบางช่วงเวลา ด้วยวิธีนี้มันยังคงดำเนินต่อไป

เครื่องกำเนิดคลื่นสามเหลี่ยม

เครื่องกำเนิดคลื่นสามเหลี่ยมเป็นวงจรอิเล็กทรอนิกส์ซึ่งสร้างคลื่นสามเหลี่ยม block diagram ของเครื่องกำเนิดคลื่นสามเหลี่ยมแสดงในรูปต่อไปนี้ -

แผนภาพบล็อกของเครื่องกำเนิดคลื่นสามเหลี่ยมประกอบด้วยสองช่วงตึกส่วนใหญ่คือเครื่องกำเนิดคลื่นสี่เหลี่ยมและตัวรวม สองบล็อกนี้คือcascaded. นั่นหมายความว่าเอาต์พุตของเครื่องกำเนิดคลื่นสี่เหลี่ยมถูกนำไปใช้เป็นอินพุตของอินทิเกรเตอร์ โปรดสังเกตว่าการรวมคลื่นสี่เหลี่ยมไม่ได้เป็นเพียงคลื่นสามเหลี่ยม

circuit diagram ของเครื่องกำเนิดคลื่นสามเหลี่ยมที่ใช้ op-amp แสดงในรูปต่อไปนี้ -

เราได้เห็นแผนภาพวงจรของเครื่องกำเนิดคลื่นสี่เหลี่ยมและอินทิเกรเตอร์แล้ว สังเกตว่าเราได้รับข้างต้นcircuit diagram ของเครื่องกำเนิดคลื่นสามเหลี่ยมที่ใช้ op-amp โดยแทนที่บล็อกด้วยแผนภาพวงจรตามลำดับในแผนภาพบล็อกของเครื่องกำเนิดคลื่นสามเหลี่ยม

555 Timer IC ได้ชื่อมาจากทั้งสาม $5K\Omega$ตัวต้านทานที่ใช้ในเครือข่ายตัวแบ่งแรงดันไฟฟ้า IC นี้มีประโยชน์ในการสร้างความล่าช้าและการสั่นของเวลาที่แม่นยำ บทนี้จะอธิบายรายละเอียดเกี่ยวกับ 555 Timer

Pin Diagram และ Functional Diagram

ในส่วนนี้ก่อนอื่นให้เราพูดคุยเกี่ยวกับแผนภาพพินของ 555 Timer IC และแผนภาพการทำงาน

พินไดอะแกรม

555 Timer IC เป็นแพคเกจ Dual-Inline ขนาดเล็ก 8 พิน (DIP) pin diagram ของ 555 Timer IC แสดงดังรูปต่อไปนี้ -

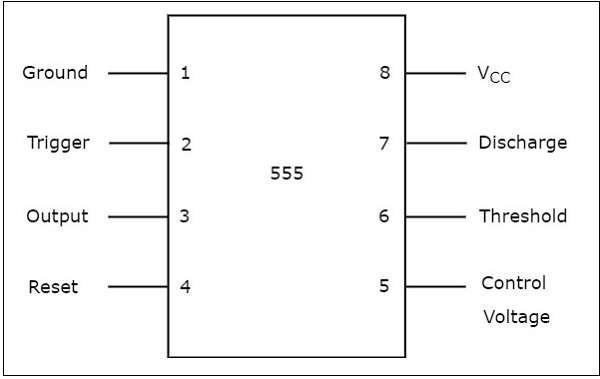
ความสำคัญของแต่ละพินสามารถอธิบายได้ด้วยตนเองจากแผนภาพด้านบน 555 Timer IC นี้สามารถทำงานโดยใช้แหล่งจ่ายไฟ DC ที่ + 5V ถึง + 18V ส่วนใหญ่มีประโยชน์ในการสร้างnon-sinusoidal รูปคลื่นเช่นสี่เหลี่ยมจัตุรัสทางลาดพัลส์และอื่น ๆ

แผนภาพการทำงาน

การแสดงภาพที่แสดงรายละเอียดภายในของ 555 Timer เรียกว่าแผนภาพการทำงาน

functional diagram ของ 555 Timer IC แสดงดังรูปต่อไปนี้ -

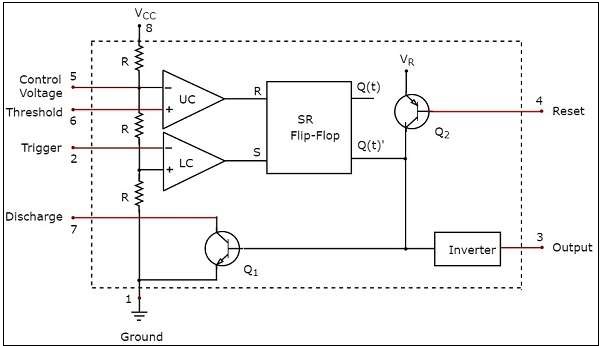
สังเกตว่าแผนภาพการทำงานของ 555 Timer ประกอบด้วยเครือข่ายตัวแบ่งแรงดันไฟฟ้าตัวเปรียบเทียบสองตัวฟลิปฟล็อป SR หนึ่งตัวทรานซิสเตอร์สองตัวและอินเวอร์เตอร์ ส่วนนี้จะกล่าวถึงวัตถุประสงค์ของแต่ละบล็อกหรือส่วนประกอบโดยละเอียด -

เครือข่ายตัวแบ่งแรงดันไฟฟ้า

เครือข่ายตัวแบ่งแรงดันไฟฟ้าประกอบด้วยสาม $5K\Omega$ ตัวต้านทานที่เชื่อมต่อแบบอนุกรมระหว่างแรงดันไฟฟ้า $V_{cc}$ และพื้นดิน
เครือข่ายนี้ให้แรงดันไฟฟ้า $\frac{V_{cc} }{3}$ ระหว่างจุดและพื้นดินหากมีเพียงจุดเดียว $5K\Omega$ตัวต้านทาน ในทำนองเดียวกันจะให้แรงดันไฟฟ้า$\frac{2V_{cc} }{3}$ ระหว่างจุดและพื้นดินหากมีเพียงสองจุด $5K\Omega$ ตัวต้านทาน

เครื่องเปรียบเทียบ

แผนภาพการทำงานของ 555 Timer IC ประกอบด้วยตัวเปรียบเทียบสองตัว ได้แก่ Upper Comparator (UC) และ Lower Comparator (LC)
จำได้ว่าก comparator เปรียบเทียบอินพุตสองอินพุตที่ใช้กับอินพุตและสร้างเอาต์พุต
หากแรงดันไฟฟ้าที่มีอยู่ที่ขั้วที่ไม่กลับหัวของ op-amp มากกว่าแรงดันไฟฟ้าที่มีอยู่ที่ขั้วต่อกลับด้านเอาต์พุตของตัวเปรียบเทียบจะเป็น $+V_{sat}$. ซึ่งถือได้ว่าเป็นLogic High ('1') ในการแทนค่าดิจิทัล
หากแรงดันไฟฟ้าที่มีอยู่ที่ขั้วที่ไม่กลับหัวของ op-amp น้อยกว่าหรือเท่ากับแรงดันไฟฟ้าที่ขั้วกลับด้านเอาต์พุตของตัวเปรียบเทียบจะเป็น $-V_{sat}$. ซึ่งถือได้ว่าเป็นLogic Low ('0') ในการแทนค่าดิจิทัล

SR Flip-Flop

จำได้ว่าก SR flip-flopทำงานด้วยการเปลี่ยนนาฬิกาเป็นบวกหรือการเปลี่ยนนาฬิกาเชิงลบ มีสองอินพุต: S และ R และสองเอาต์พุต: Q (t) และ Q (t) ' เอาต์พุต Q (t) & Q (t) 'เป็นส่วนเสริมซึ่งกันและกัน
ตารางต่อไปนี้แสดงไฟล์ state table ของ SR flip-flop

ส	ร	Q (เสื้อ + 1)
0	0	Q (เสื้อ)
0	1	0
1	0	1
1	1	-

ที่นี่ Q (t) & Q (t + 1) คือสถานะปัจจุบันและสถานะถัดไปตามลำดับ ดังนั้น SR flip-flop สามารถใช้กับหนึ่งในสามฟังก์ชั่นนี้เช่น Hold, Reset & Set ตามเงื่อนไขการป้อนข้อมูลเมื่อมีการใช้การเปลี่ยนสัญญาณนาฬิกาเป็นบวก (ลบ)
เอาต์พุตของตัวเปรียบเทียบล่าง (LC) และตัวเปรียบเทียบบน (UC) ถูกนำไปใช้เป็น inputs of SR flip-flop ดังแสดงในแผนภาพการทำงานของ 555 Timer IC

ทรานซิสเตอร์และอินเวอร์เตอร์

แผนภาพการทำงานของ 555 Timer IC ประกอบด้วยทรานซิสเตอร์ npn หนึ่งตัว $Q_{1}$ และทรานซิสเตอร์ pnp หนึ่งตัว $Q_{2}$. ทรานซิสเตอร์ npn$Q_{1}$จะเปิดขึ้นหากแรงดันไฟฟ้าฐานไปยังตัวปล่อยเป็นบวกและมากกว่าแรงดันไฟฟ้าตัด มิฉะนั้นจะถูกปิด
ทรานซิสเตอร์ pnp $Q_{2}$ ใช้เป็น buffer เพื่อแยกอินพุตรีเซ็ตออกจากทรานซิสเตอร์ฟลิปฟล็อป SR และทรานซิสเตอร์ npn $Q_{1}$.
inverter ใช้ในแผนภาพการทำงานของ 555 Timer IC ไม่เพียง แต่ดำเนินการกลับด้านเท่านั้น แต่ยังช่วยขยายระดับพลังงานอีกด้วย

555 Timer IC สามารถใช้ในการทำงานที่เสถียรแบบโมโนเพื่อสร้างพัลส์ที่เอาต์พุต ในทำนองเดียวกันสามารถใช้ในการทำงานแบบ astable เพื่อสร้างคลื่นสี่เหลี่ยมที่เอาต์พุต

เฟสล็อคลูป (PLL)เป็นหนึ่งในบล็อกที่สำคัญในระบบเชิงเส้น มีประโยชน์ในระบบการสื่อสารเช่นเรดาร์ดาวเทียม FM เป็นต้น

บทนี้จะกล่าวถึงบล็อกไดอะแกรมของ PLL และ IC 565 โดยละเอียด

แผนภาพบล็อกของ PLL

Phase Locked Loop (PLL) ส่วนใหญ่ประกอบด้วยสิ่งต่อไปนี้ three blocks -

เครื่องตรวจจับเฟส
ตัวกรองความถี่ต่ำที่ใช้งานอยู่
Oscillator ควบคุมแรงดันไฟฟ้า (VCO)

block diagram ของ PLL แสดงในรูปต่อไปนี้ -

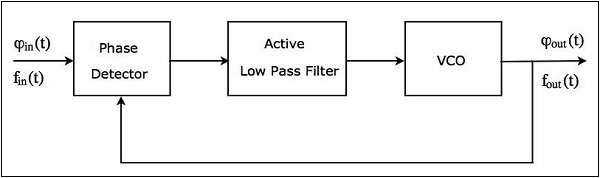
เอาต์พุตของเครื่องตรวจจับเฟสถูกนำไปใช้เป็นอินพุตของตัวกรองความถี่ต่ำที่ใช้งานอยู่ ในทำนองเดียวกันเอาต์พุตของตัวกรองความถี่ต่ำที่ใช้งานจะถูกนำไปใช้เป็นอินพุตของ VCO

working ของ PLL มีดังนี้ -

Phase detector สร้างแรงดันไฟฟ้ากระแสตรงซึ่งเป็นสัดส่วนกับความแตกต่างของเฟสระหว่างสัญญาณอินพุตที่มีความถี่ $f_{in}$ และสัญญาณตอบรับ (เอาต์พุต) ที่มีความถี่ $f_{out}$.
ก Phase detector เป็นตัวคูณและสร้างส่วนประกอบความถี่สองส่วนที่เอาต์พุต - ผลรวมของความถี่ $f_{in}$ และ $f_{out}$ และความแตกต่างของความถี่ $f_{in}$ & $f_{out}$.
อัน active low pass filterสร้างแรงดันไฟฟ้ากระแสตรงที่เอาต์พุตหลังจากกำจัดส่วนประกอบความถี่สูงที่มีอยู่ในเอาต์พุตของเครื่องตรวจจับเฟส นอกจากนี้ยังขยายสัญญาณ
ก VCOสร้างสัญญาณที่มีความถี่หนึ่งเมื่อไม่มีอินพุตที่ใช้กับมัน ความถี่นี้สามารถเลื่อนไปด้านใดด้านหนึ่งได้โดยใช้แรงดันไฟฟ้ากระแสตรง ดังนั้นค่าเบี่ยงเบนความถี่จึงเป็นสัดส่วนโดยตรงกับแรงดันไฟฟ้ากระแสตรงที่เอาต์พุตของตัวกรองความถี่ต่ำ

การดำเนินการข้างต้นจะเกิดขึ้นจนกว่าความถี่ VCO จะเท่ากับความถี่สัญญาณอินพุต ขึ้นอยู่กับประเภทของแอปพลิเคชันเราสามารถใช้เอาต์พุตของตัวกรองความถี่ต่ำที่ใช้งานอยู่หรือเอาต์พุตของ VCO PLL ถูกใช้ในหลาย ๆapplications เช่น FM demodulator เครื่องกำเนิดนาฬิกาเป็นต้น

PLL ทำงานในรูปแบบ following three modes -

โหมดการทำงานฟรี
โหมดถ่ายภาพ
โหมดล็อค

ในขั้นต้น PLL ดำเนินการใน free running modeเมื่อไม่มีการใช้อินพุตกับมัน เมื่อสัญญาณอินพุตที่มีความถี่บางส่วนถูกนำไปใช้กับ PLL ความถี่สัญญาณเอาต์พุตของ VCO จะเริ่มเปลี่ยนไป ในขั้นตอนนี้ PLL ถูกกล่าวว่ากำลังดำเนินการในรูปแบบcapture mode. ความถี่สัญญาณเอาต์พุตของ VCO จะเปลี่ยนไปเรื่อย ๆ จนกว่าจะเท่ากับความถี่สัญญาณอินพุต ตอนนี้มีการกล่าวกันว่า PLL กำลังทำงานในไฟล์lock mode.

IC 565

IC 565 เป็นไอซีเฟสล็อกลูปที่ใช้บ่อยที่สุด เป็นแพ็คเกจ Dual-Inline (DIP) 14 พิน pin diagram ของ IC 565 แสดงดังรูปต่อไปนี้ -

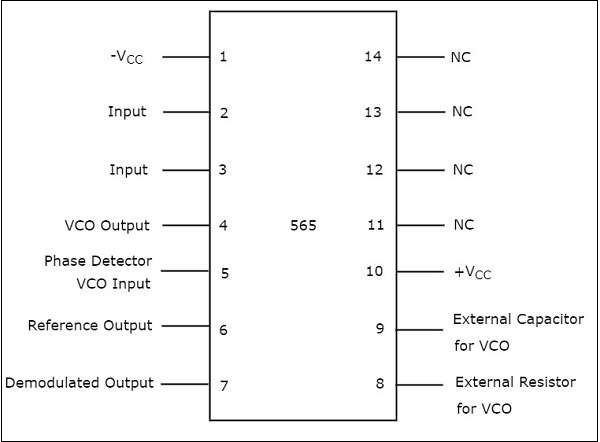
จุดประสงค์ของแต่ละพินสามารถอธิบายได้ด้วยตนเองจากแผนภาพด้านบน จาก 14 พินมีเพียง 10 พิน (หมายเลขพิน 1 ถึง 10) เท่านั้นที่ใช้สำหรับการทำงานของ PLL ดังนั้นหมุด 4 ตัวที่เหลือ (หมายเลขพิน 11 ถึง 14) จึงมีป้าย NC (No Connection)

VCOสร้างเอาต์พุตที่พินหมายเลข 4 ของ IC 565 เมื่อหมายเลขพิน 2 และ 3 ต่อสายดิน ในทางคณิตศาสตร์เราสามารถเขียนความถี่เอาต์พุต$f_{out}$ ของ VCO เป็น.

$$f_{out}=\frac{0.25}{R_VC_V}$$

ที่ไหน

$R_{V}$ คือตัวต้านทานภายนอกที่เชื่อมต่อกับพินหมายเลข 8

$C_{V}$ คือตัวเก็บประจุภายนอกที่เชื่อมต่อกับพินหมายเลข 9

โดยเลือกค่าที่เหมาะสมของ $R_{V}$ และ $C_{V}$เราสามารถแก้ไข (กำหนด) ความถี่เอาต์พุต $f_{out}$ ของ VCO
Pin numbers 4 and 5จะต้องลัดวงจรด้วยสายไฟภายนอกเพื่อให้สามารถใช้เอาต์พุตของ VCO เป็นหนึ่งในอินพุตของเครื่องตรวจจับเฟส
IC 565 มีความต้านทานภายในเท่ากับ $3.6K\Omega$. ต้องเชื่อมต่อตัวเก็บประจุ C ระหว่างหมายเลขพิน 7 และ 10 เพื่อสร้างไฟล์low pass filter ด้วยความต้านทานภายในนั้น

โปรดทราบว่าตามข้อกำหนดเราต้องกำหนดค่าพินของ IC 565 อย่างถูกต้อง

ฟังก์ชันของไฟล์ voltage regulatorคือการรักษาแรงดันไฟฟ้ากระแสตรงให้คงที่ที่เอาต์พุตโดยไม่คำนึงถึงความผันผวนของแรงดันไฟฟ้าที่อินพุตและ (หรือ) การเปลี่ยนแปลงของกระแสโหลด กล่าวอีกนัยหนึ่งตัวควบคุมแรงดันไฟฟ้าจะสร้างแรงดันเอาต์พุต DC ที่มีการควบคุม

นอกจากนี้ยังมีตัวควบคุมแรงดันไฟฟ้าในรูปแบบวงจรรวม (IC) สิ่งเหล่านี้เรียกว่าvoltage regulator ICs.

ประเภทของตัวควบคุมแรงดันไฟฟ้า

มี two types ของตัวควบคุมแรงดันไฟฟ้า -

ตัวควบคุมแรงดันไฟฟ้าคงที่
ตัวควบคุมแรงดันไฟฟ้าที่ปรับได้

บทนี้จะกล่าวถึงเกี่ยวกับตัวควบคุมแรงดันไฟฟ้าทั้งสองประเภทนี้ทีละตัว

ตัวควบคุมแรงดันไฟฟ้าคงที่

ก fixed voltage regulatorสร้างแรงดันไฟฟ้าขาออกคงที่ซึ่งเป็นบวกหรือลบ กล่าวอีกนัยหนึ่งตัวควบคุมแรงดันไฟฟ้าคงที่บางตัวจะสร้างค่าแรงดันไฟฟ้ากระแสตรงคงที่เป็นบวกในขณะที่บางตัวสร้างค่าแรงดัน DC คงที่เป็นลบ

78xx ไอซีควบคุมแรงดันไฟฟ้าสร้างค่าแรงดันไฟฟ้ากระแสตรงคงที่เป็นบวกในขณะที่ไอซีควบคุมแรงดันไฟฟ้า 79xx จะสร้างค่าแรงดันไฟฟ้ากระแสตรงคงที่เป็นลบ

ควรสังเกตประเด็นต่อไปนี้ขณะใช้งาน 78xx และ 79xx ไอซีควบคุมแรงดันไฟฟ้า -

“ xx” หมายถึงตัวเลขสองหลักและแสดงถึงจำนวน (ขนาด) ของแรงดันไฟฟ้าที่ IC ควบคุมแรงดันไฟฟ้าผลิตขึ้น
ไอซีควบคุมแรงดันไฟฟ้าทั้ง 78xx และ 79xx มี 3 pins แต่ละพินและพินที่สามใช้สำหรับรวบรวมเอาต์พุตจากพวกเขา
วัตถุประสงค์ของพินแรกและตัวที่สองของ IC ทั้งสองประเภทนี้แตกต่างกัน -
- หมุดแรกและตัวที่สองของ 78xx ไอซีควบคุมแรงดันไฟฟ้าใช้สำหรับเชื่อมต่ออินพุตและกราวด์ตามลำดับ
- หมุดแรกและตัวที่สองของ 79xx ไอซีควบคุมแรงดันไฟฟ้าใช้สำหรับเชื่อมต่อกราวด์และอินพุตตามลำดับ

ตัวอย่าง

IC ควบคุมแรงดันไฟฟ้า 7805 สร้างแรงดันไฟฟ้า DC ที่ +5 โวลต์
IC ควบคุมแรงดันไฟฟ้า 7905 สร้างแรงดันไฟฟ้ากระแสตรง -5 โวลต์

รูปต่อไปนี้แสดงวิธีการสร้างไฟล์ fixed positive voltage ที่เอาต์พุตโดยใช้ตัวควบคุมแรงดันไฟฟ้าบวกคงที่พร้อมการเชื่อมต่อที่จำเป็น

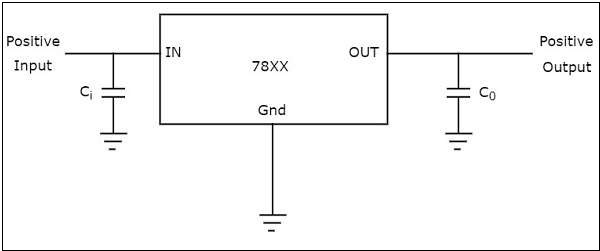
ในรูปด้านบนที่แสดงตัวควบคุมแรงดันไฟฟ้าบวกคงที่ตัวเก็บประจุอินพุต C _iใช้เพื่อป้องกันการสั่นที่ไม่ต้องการและตัวเก็บประจุเอาท์พุท C ₀ทำหน้าที่เป็นตัวกรองเส้นเพื่อปรับปรุงการตอบสนองชั่วคราว

Note - รับ fixed negative voltage ที่เอาต์พุตโดยใช้ตัวควบคุมแรงดันไฟฟ้าลบคงที่พร้อมการเชื่อมต่อที่เหมาะสม

ตัวควบคุมแรงดันไฟฟ้าที่ปรับได้

ตัวควบคุมแรงดันไฟฟ้าที่ปรับได้จะสร้างแรงดันเอาต์พุต DC ซึ่งสามารถปรับเป็นค่าอื่น ๆ ของช่วงแรงดันไฟฟ้าที่กำหนดได้ ดังนั้นตัวควบคุมแรงดันไฟฟ้าที่ปรับได้จึงเรียกอีกอย่างว่า avariable voltage regulator.

ค่าแรงดันเอาต์พุต DC ของตัวควบคุมแรงดันไฟฟ้าที่ปรับได้อาจเป็นค่าบวกหรือลบก็ได้

LM317 IC ควบคุมแรงดันไฟฟ้า

LM317 IC ควบคุมแรงดันไฟฟ้าสามารถใช้สำหรับสร้างค่าแรงดันไฟฟ้ากระแสตรงที่เป็นบวกที่ต้องการของช่วงแรงดันไฟฟ้าที่มีอยู่

LM317 ตัวควบคุมแรงดันไฟฟ้า IC มี 3 พิน ขาแรกใช้สำหรับปรับแรงดันขาออกขาที่สองใช้สำหรับรวบรวมเอาท์พุทและขาที่สามใช้สำหรับเชื่อมต่ออินพุท

พินที่ปรับได้ (เทอร์มินัล) มาพร้อมกับตัวต้านทานแบบแปรผันซึ่งช่วยให้เอาต์พุตแตกต่างกันระหว่างช่วงกว้าง

รูปด้านบนแสดงแหล่งจ่ายไฟที่ไม่มีการควบคุมซึ่งขับ IC ตัวควบคุมแรงดันไฟฟ้า LM 317 ซึ่งมักใช้กันทั่วไป IC นี้สามารถจ่ายกระแสโหลด 1.5A ในช่วงเอาต์พุตที่ปรับได้ตั้งแต่ 1.25 V ถึง 37 V.

ปริมาณในโลกแห่งความเป็นจริงทั้งหมดเป็นแบบอะนาล็อก เราสามารถแสดงปริมาณเหล่านี้ทางไฟฟ้าเป็นสัญญาณแอนะล็อก อันanalog signal เป็นสัญญาณที่แปรผันตามเวลาที่มีค่าจำนวนเท่าใดก็ได้ (รูปแบบต่างๆ) สำหรับช่วงเวลาที่กำหนด

ตรงกันข้ามกับสิ่งนี้ก digital signal แตกต่างกันไปในแต่ละระดับอย่างกะทันหันและจะมีค่าจำนวน จำกัด (รูปแบบต่างๆ) สำหรับช่วงเวลาที่กำหนด

บทนี้จะกล่าวถึงประเภทของตัวแปลงข้อมูลและข้อกำหนด

ประเภทของตัวแปลงข้อมูล

วงจรอิเล็กทรอนิกส์ซึ่งสามารถทำงานด้วยสัญญาณแอนะล็อกเรียกว่าวงจรอนาล็อก ในทำนองเดียวกันวงจรอิเล็กทรอนิกส์ซึ่งสามารถทำงานด้วยสัญญาณดิจิทัลเรียกว่าวงจรดิจิทัล ตัวแปลงข้อมูลคือวงจรอิเล็กทรอนิกส์ที่แปลงข้อมูลจากรูปแบบหนึ่งไปเป็นอีกรูปแบบหนึ่ง

มีสอง types of data converters -

ตัวแปลงอนาล็อกเป็นดิจิตอล
ตัวแปลงดิจิตอลเป็นอนาล็อก

หากเราต้องการเชื่อมต่อเอาท์พุทของวงจรอนาล็อกเป็นอินพุตของวงจรดิจิทัลเราจะต้องวางวงจรเชื่อมต่อระหว่างวงจรเหล่านั้น วงจรเชื่อมต่อที่แปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัลเรียกว่าเป็นAnalog to Digital Converter.

ในทำนองเดียวกันถ้าเราต้องการเชื่อมต่อเอาท์พุทของวงจรดิจิทัลเป็นอินพุตของวงจรอนาล็อกเราจะต้องวางวงจรเชื่อมต่อระหว่างวงจรเหล่านั้น วงจรเชื่อมต่อที่แปลงสัญญาณดิจิทัลเป็นสัญญาณแอนะล็อกเรียกว่าเป็นDigital to Analog Converter.

โปรดทราบว่าตัวแปลงอนาล็อกเป็นดิจิตอลบางตัวอาจต้องการตัวแปลงดิจิทัลเป็นอนาล็อกเป็นบล็อกภายในสำหรับการทำงาน

ข้อมูลจำเพาะ

ต่อไปนี้คือไฟล์ specifications ที่เกี่ยวข้องกับการแปลงข้อมูล -

Resolution
เวลาแปลง

ความละเอียด

ความละเอียดคือ minimum amount of changeจำเป็นในแรงดันไฟฟ้าอินพุตแบบอะนาล็อกเพื่อให้แสดงในเอาต์พุตไบนารี (ดิจิตอล) ขึ้นอยู่กับจำนวนบิตที่ใช้ในเอาต์พุตดิจิทัล

Mathematicallyความละเอียดสามารถแสดงเป็น

$$Resolution=\frac{1}{2^{N}}$$

โดยที่ 'N' คือจำนวนบิตที่มีอยู่ในเอาต์พุตดิจิทัล

จากสูตรข้างต้นเราสามารถสังเกตได้ว่ามีไฟล์ inverse relationshipระหว่างความละเอียดและจำนวนบิต ดังนั้นความละเอียดจะลดลงเมื่อจำนวนบิตเพิ่มขึ้นและในทางกลับกัน

Resolution ยังสามารถกำหนดเป็นอัตราส่วนของแรงดันไฟฟ้าอินพุตแบบอนาล็อกสูงสุดที่สามารถแสดงเป็นเลขฐานสองและเลขฐานสองที่เท่ากัน

Mathematicallyความละเอียดสามารถแสดงเป็น

$$Resolution=\frac{V_{FS}}{2^{N}-1}$$

ที่ไหน

$V_{FS}$ คือแรงดันไฟฟ้าอินพุตเต็มสเกลหรือแรงดันไฟฟ้าอินพุตอะนาล็อกสูงสุด

'N' คือจำนวนบิตที่มีอยู่ในเอาต์พุตดิจิทัล

เวลาแปลง

ระยะเวลาที่ต้องใช้สำหรับตัวแปลงข้อมูลเพื่อแปลงข้อมูล (ข้อมูล) ของรูปแบบหนึ่งเป็นข้อมูลที่เทียบเท่าในรูปแบบอื่นเรียกว่าเป็น conversion time. เนื่องจากเรามีตัวแปลงข้อมูลสองประเภทเวลาในการแปลงจึงมีสองประเภทดังนี้

เวลาแปลงอนาล็อกเป็นดิจิตอล
เวลาแปลงดิจิตอลเป็นอนาล็อก

ระยะเวลาที่ต้องใช้สำหรับตัวแปลงอนาล็อกเป็นดิจิตอล (ADC) ในการแปลงแรงดันไฟฟ้าอินพุตแบบอะนาล็อกเป็นเอาต์พุตไบนารี (ดิจิตอล) ที่เทียบเท่ากันเรียกว่า Analog to Digital conversion time. ขึ้นอยู่กับจำนวนบิตที่ใช้ในเอาต์พุตดิจิทัล

ระยะเวลาที่ต้องใช้สำหรับ Digital to Analog Converter (DAC) ในการแปลงอินพุตไบนารี (ดิจิตอล) ให้เป็นแรงดันเอาต์พุตแบบอะนาล็อกที่เทียบเท่ากันเรียกว่า Digital to Analog conversion time. ขึ้นอยู่กับจำนวนบิตที่มีอยู่ในอินพุตไบนารี (ดิจิทัล)

ก Digital to Analog Converter (DAC)แปลงสัญญาณอินพุตดิจิทัลเป็นสัญญาณเอาท์พุตอนาล็อก สัญญาณดิจิทัลแสดงด้วยรหัสไบนารีซึ่งเป็นการรวมกันของบิต 0 และ 1 ในบทนี้เกี่ยวกับตัวแปลงดิจิตอลเป็นอนาล็อกโดยละเอียด

block diagram ของ DAC แสดงในรูปต่อไปนี้ -

Digital to Analog Converter (DAC) ประกอบด้วยอินพุตไบนารีจำนวนหนึ่งและเอาต์พุตเดียว โดยทั่วไปแล้วไฟล์number of binary inputs ของ DAC จะมีกำลังสอง

ประเภทของ DAC

มี two types ของ DAC

ตัวต้านทานถ่วงน้ำหนัก DAC
บันได R-2R DAC

ส่วนนี้กล่าวถึงรายละเอียดเกี่ยวกับ DAC ทั้งสองประเภทนี้ -

ตัวต้านทานถ่วงน้ำหนัก DAC

ตัวต้านทานแบบถ่วงน้ำหนัก DAC จะสร้างเอาต์พุตแบบอะนาล็อกซึ่งเกือบจะเท่ากับอินพุตดิจิตอล (ไบนารี) โดยใช้ binary weighted resistorsในวงจรแอดเดอร์กลับด้าน ในระยะสั้นตัวต้านทานแบบถ่วงน้ำหนักไบนารี DAC เรียกว่าตัวต้านทานแบบถ่วงน้ำหนัก DAC

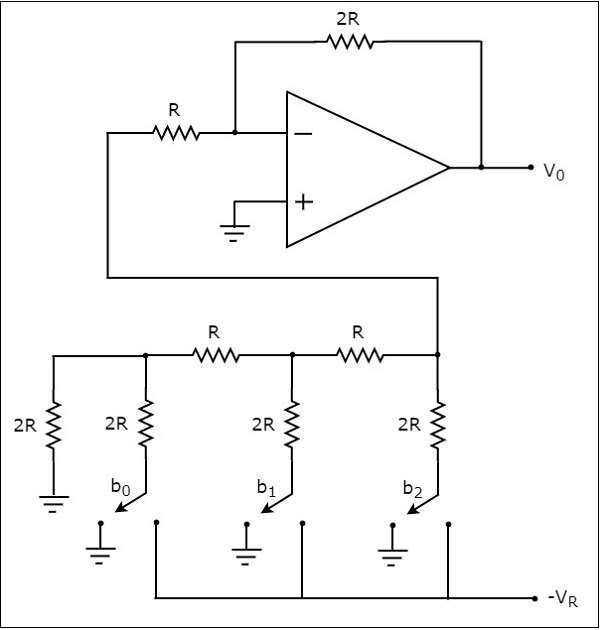
circuit diagram ของตัวต้านทานแบบถ่วงน้ำหนักไบนารี 3 บิต DAC แสดงในรูปต่อไปนี้ -

จำไว้ว่าบิตของเลขฐานสองสามารถมีได้เพียงหนึ่งในสองค่าเท่านั้น กล่าวคือ 0 หรือ 1 ปล่อยให้3-bit binary input คือ $b_{2}b_{1}b_{0}$. นี่คือบิต$b_{2}$ และ $b_{0}$ แสดงถึง Most Significant Bit (MSB) and Least Significant Bit (LSB) ตามลำดับ

digital switchesแสดงในรูปด้านบนจะเชื่อมต่อกับกราวด์เมื่อบิตอินพุตที่เกี่ยวข้องมีค่าเท่ากับ '0' ในทำนองเดียวกันสวิตช์ดิจิตอลที่แสดงในรูปด้านบนจะเชื่อมต่อกับแรงดันอ้างอิงเชิงลบ$-V_{R}$ เมื่อบิตอินพุตที่สอดคล้องกันเท่ากับ '1'

ให้เป็นไปตาม virtual short conceptแรงดันไฟฟ้าที่ขั้วอินพุตกลับด้านของ opamp จะเหมือนกับแรงดันไฟฟ้าที่มีอยู่ที่ขั้วอินพุตที่ไม่กลับด้าน ดังนั้นแรงดันไฟฟ้าที่โหนดของขั้วอินพุตกลับด้านจะเป็นศูนย์โวลต์

nodal equation ที่โหนดของขั้วอินพุตกลับด้านคือ:

$$\frac{0+V_{R}b_{2}}{2^{0}R}+\frac{0+V_{R}b_{1}}{2^{1}R}+\frac{0+V_{R}b_{0}}{2^{2}R}+\frac{0-V_{0}}{R_{f}}=0$$

$$=>\frac{V_{0}}{R_{f}}=\frac{V_{R}b_{2}}{2^{0}R}+\frac{V_{R}b_{1}}{2^{1}R}+\frac{V_{R}b_{0}}{2^{2}R}$$

$$=>V_{0}=\frac{V_{R}R_{f}}{R}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

การเปลี่ยนตัว $R=2R_{f}$ ในสมการข้างต้น

$$=>V_{0}=\frac{V_{R}R_{f}}{2R_{f}}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

$$=>V_{0}=\frac{V_{R}}{2}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

สมการข้างต้นแสดงถึง output voltage equationของตัวต้านทานแบบถ่วงน้ำหนักไบนารี 3 บิต DAC เนื่องจากจำนวนบิตเป็นสามในอินพุตไบนารี (ดิจิตอล) เราจะได้รับค่าแรงดันขาออกที่เป็นไปได้เจ็ดค่าโดยการเปลี่ยนอินพุตไบนารีจาก 000 ถึง 111 สำหรับแรงดันอ้างอิงคงที่$V_{R}$.

เราสามารถเขียนไฟล์ generalized output voltage equation ของตัวต้านทานแบบถ่วงน้ำหนักไบนารี N-bit DAC ดังแสดงด้านล่างตามสมการแรงดันเอาต์พุตของตัวต้านทานแบบถ่วงน้ำหนักไบนารี 3 บิต DAC

$$=>V_{0}=\frac{V_{R}}{2}\left \{ \frac{b_{N-1}}{2^{0}}+ \frac{b_{N-2}}{2^{1}}+....+\frac{b_{0}}{2^{N-1}} \right \}$$

The disadvantages ของตัวต้านทานแบบถ่วงน้ำหนักไบนารี DAC มีดังนี้ -

ความแตกต่างระหว่างค่าความต้านทานที่สอดคล้องกับ LSB & MSB จะเพิ่มขึ้นเมื่อจำนวนบิตที่มีอยู่ในอินพุตดิจิทัลเพิ่มขึ้น
เป็นการยากที่จะออกแบบตัวต้านทานที่แม่นยำยิ่งขึ้นเนื่องจากจำนวนบิตที่มีอยู่ในอินพุตดิจิทัลเพิ่มขึ้น

บันได R-2R DAC

บันได R-2R DAC เอาชนะข้อเสียของตัวต้านทานแบบถ่วงน้ำหนักไบนารี DAC ตามชื่อที่แนะนำ R-2R Ladder DAC สร้างเอาต์พุตแบบอะนาล็อกซึ่งเกือบจะเท่ากับอินพุตดิจิตอล (ไบนารี) โดยใช้ aR-2R ladder network ในวงจรแอดเดอร์กลับด้าน

Thecircuit diagramของบันได 3 บิต R-2R DAC แสดงในรูปต่อไปนี้ -

จำไว้ว่าบิตของเลขฐานสองสามารถมีได้เพียงหนึ่งในสองค่าเท่านั้น กล่าวคือ 0 หรือ 1 ปล่อยให้3-bit binary input คือ $b_{2}b_{1}b_{0}$. นี่คือบิต$b_{2}$ และ $b_{0}$ หมายถึงบิตที่มีนัยสำคัญที่สุด (MSB) และบิตที่มีนัยสำคัญน้อยที่สุด (LSB) ตามลำดับ

สวิตช์ดิจิตอลที่แสดงในรูปด้านบนจะเชื่อมต่อกับกราวด์เมื่อบิตอินพุตที่เกี่ยวข้องมีค่าเท่ากับ '0' ในทำนองเดียวกันสวิตช์ดิจิตอลที่แสดงในรูปด้านบนจะเชื่อมต่อกับแรงดันอ้างอิงเชิงลบ$-V_{R}$ เมื่อบิตอินพุตที่สอดคล้องกันเท่ากับ '1'

เป็นเรื่องยากที่จะได้สมการแรงดันเอาต์พุตทั่วไปของบันได R-2R DAC แต่เราสามารถหาค่าแรงดันเอาต์พุตแบบอะนาล็อกของ R-2R Ladder DAC สำหรับชุดค่าผสมไบนารีแต่ละชุดได้อย่างง่ายดาย

advantages ของบันได R-2R DAC มีดังนี้ -

บันได R-2R DAC มีตัวต้านทานเพียงสองค่า: R และ 2R ดังนั้นจึงง่ายต่อการเลือกและออกแบบตัวต้านทานที่แม่นยำยิ่งขึ้น
หากมีจำนวนบิตมากขึ้นในอินพุตดิจิทัลเราจะต้องรวมจำนวนส่วน R-2R ที่ต้องการเพิ่มเติมด้วย

เนื่องจากข้อดีข้างต้น R-2R Ladder DAC จึงเป็นที่นิยมมากกว่าตัวต้านทานแบบถ่วงน้ำหนักไบนารี DAC

ในบทที่แล้วเราได้พูดถึง DAC สองประเภท บทนี้จะกล่าวถึงปัญหาตัวอย่างที่อ้างอิงตามบันได R-2R DAC

ตัวอย่าง

ให้เราหาค่าของแรงดันเอาต์พุตแบบอะนาล็อกของ R-2R Ladder DAC สำหรับอินพุตไบนารี $b_{2}b_{1}b_{0}$ = 100.

แผนภาพวงจรและการลดความซับซ้อน

circuit diagram ของบันได 3 บิต R-2R DAC เมื่ออินพุตไบนารี $b_{2}b_{1}b_{0}$ = 100 นำไปใช้กับมันแสดงในรูปต่อไปนี้ -

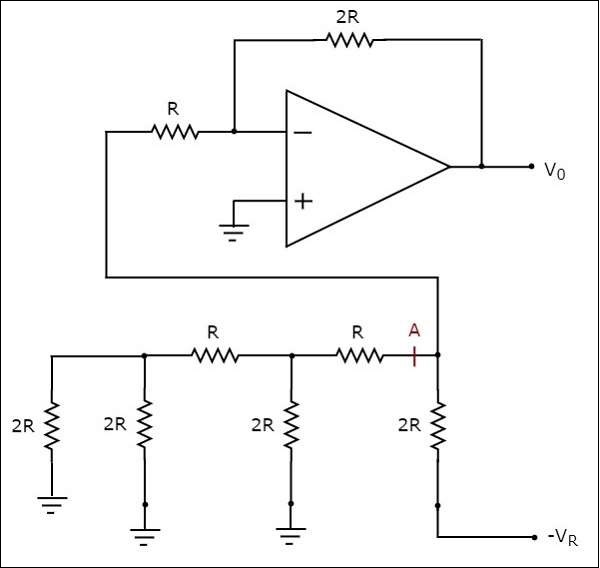
ในวงจรด้านบนมีตัวต้านทานแบบอนุกรมและแบบขนานอยู่ทางด้านซ้ายของ point Aด้วยความเคารพต่อพื้นดิน ดังนั้นเราสามารถแทนที่เครือข่ายตัวต้านทานทั้งหมดด้วยตัวต้านทานตัวเดียวที่มีความต้านทาน$2R\Omega$.

simplified circuit diagram แสดงในรูปต่อไปนี้ -

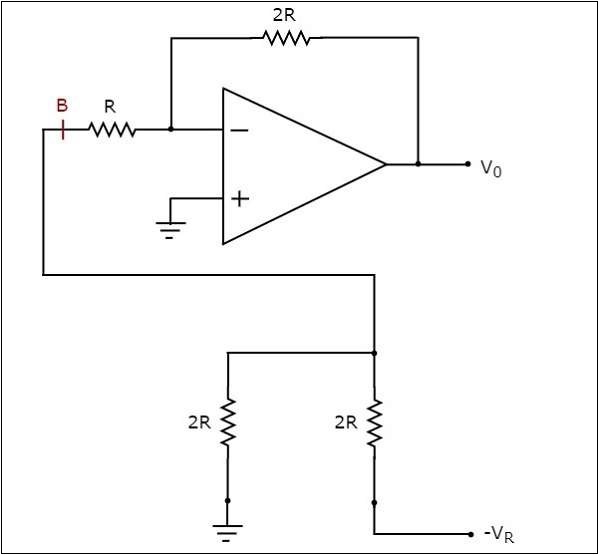
เราสามารถแทนที่ส่วนของเครือข่ายที่เชื่อมต่อทางด้านซ้ายของจุด B เทียบกับกราวด์โดยใช้วงจรเทียบเท่าของ Thevenin modified circuit diagram แสดงในรูปต่อไปนี้ -

ในวงจรข้างต้นมีชุดตัวต้านทานสองตัวรวมกัน แทนที่ชุดค่าผสมนี้ด้วยตัวต้านทานตัวเดียว สุดท้ายcircuit diagram หลังจากการทำให้เข้าใจง่ายจะแสดงในรูปต่อไปนี้ -

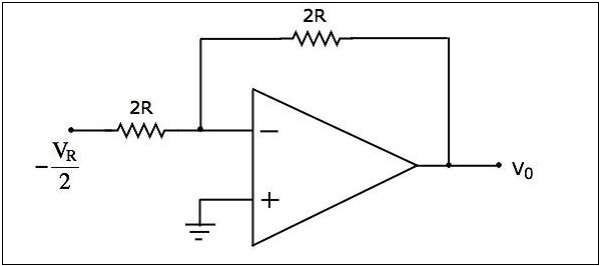
ตอนนี้แผนภาพวงจรด้านบนดูเหมือนไฟล์ inverting amplifier. มีแรงดันไฟฟ้าอินพุตเป็น$-\frac{V_{R}}{2}$ โวลต์ความต้านทานอินพุตของ $2R\Omega$ และความต้านทานข้อเสนอแนะของ $2R\Omega$.

output voltage ของวงจรที่แสดงด้านบนจะเป็น -

$$V_{0}=-\frac{2R}{2R}\left(-\frac{V_{R}}{2}\right)$$

$$V_{0}=\frac{V_{R}}{2}$$

ดังนั้นไฟล์ output voltage ของ 3-bit R-2R Ladder DAC คือ $\frac{V_{R}}{2}$ โวลต์สำหรับอินพุตไบนารี $b_{2}b_{1}b_{0}$ = 100.

ตัวแปลงอนาล็อกเป็นดิจิตอล (ADC)แปลงสัญญาณแอนะล็อกเป็นสัญญาณดิจิทัล สัญญาณดิจิทัลแสดงด้วยรหัสไบนารีซึ่งเป็นการรวมกันของบิต 0 และ 1

block diagram ของ ADC แสดงในรูปต่อไปนี้ -

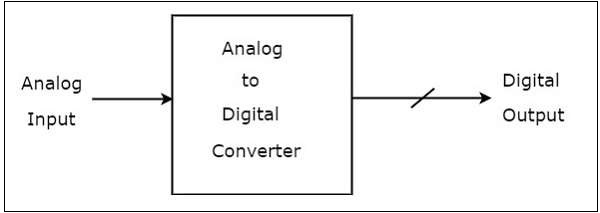
สังเกตว่าในรูปที่แสดงด้านบนตัวแปลงอนาล็อกเป็นดิจิตอล (ADC)ประกอบด้วยอินพุตอะนาล็อกเดียวและเอาต์พุตไบนารีจำนวนมาก โดยทั่วไปจำนวนเอาต์พุตไบนารีของ ADC จะมีกำลังสอง

มี two typesของ ADCs: ADC ประเภทโดยตรงและ ADC ประเภททางอ้อม บทนี้จะกล่าวถึงรายละเอียดเกี่ยวกับ ADC ประเภทโดยตรง

หาก ADC ทำการแปลงอนาล็อกเป็นดิจิทัลโดยตรงโดยใช้รหัสดิจิทัล (ไบนารี) ที่เทียบเท่าที่สร้างขึ้นภายในเพื่อเปรียบเทียบกับอินพุตแบบอะนาล็อกจะเรียกว่าเป็น Direct type ADC.

ต่อไปนี้คือไฟล์ examples ประเภท ADCs โดยตรง -

ADC แบบเคาน์เตอร์
ADC ประมาณต่อเนื่อง
ประเภทแฟลช ADC

ส่วนนี้จะกล่าวถึงรายละเอียดเกี่ยวกับ ADCs ประเภท Direct เหล่านี้

ADC แบบเคาน์เตอร์

ก counter type ADC สร้างเอาต์พุตดิจิตอลซึ่งมีค่าประมาณเท่ากับอินพุตอะนาล็อกโดยใช้การทำงานของตัวนับภายใน

block diagram ของตัวนับประเภท ADC แสดงในรูปต่อไปนี้ -

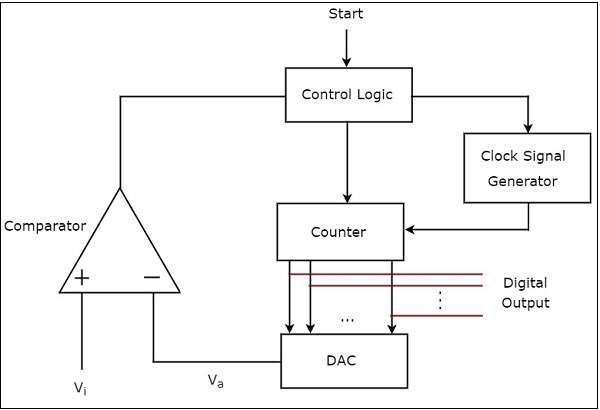
ADC ประเภทตัวนับส่วนใหญ่ประกอบด้วย 5 ช่วงตึก: ตัวสร้างสัญญาณนาฬิกา, ตัวนับ, DAC, ตัวเปรียบเทียบและตรรกะการควบคุม

working ADC ประเภทตัวนับมีดังนี้ -

control logic รีเซ็ตตัวนับและเปิดใช้งานเครื่องกำเนิดสัญญาณนาฬิกาเพื่อส่งพัลส์นาฬิกาไปยังตัวนับเมื่อได้รับสัญญาณสั่งการเริ่มต้น
counterได้รับการเพิ่มขึ้นทีละหนึ่งสำหรับพัลส์นาฬิกาทุกครั้งและค่าของมันจะอยู่ในรูปแบบไบนารี (ดิจิทัล) เอาต์พุตของตัวนับนี้ถูกนำไปใช้เป็นอินพุตของ DAC
DACแปลงอินพุตไบนารี (ดิจิตอล) ที่ได้รับซึ่งเป็นเอาต์พุตของตัวนับเป็นเอาต์พุตแบบอะนาล็อก ตัวเปรียบเทียบเปรียบเทียบค่าอะนาล็อกนี้$V_{a}$ ด้วยค่าอินพุตอะนาล็อกภายนอก $V_{i}$.
output of comparator จะ ‘1’ตราบใดที่มากกว่า การดำเนินการที่กล่าวถึงในสองขั้นตอนข้างต้นจะดำเนินต่อไปตราบเท่าที่ตรรกะการควบคุมได้รับ '1' จากเอาต์พุตของตัวเปรียบเทียบ
output of comparator จะ ‘0’ เมื่อไหร่ $V_{i}$ น้อยกว่าหรือเท่ากับ $V_{a}$. ดังนั้นตรรกะการควบคุมจึงได้รับ '0' จากเอาต์พุตของตัวเปรียบเทียบ จากนั้นตรรกะการควบคุมจะปิดใช้งานตัวสร้างสัญญาณนาฬิกาเพื่อไม่ให้ส่งพัลส์นาฬิกาไปที่เคาน์เตอร์
ในทันทีนี้ผลลัพธ์ของตัวนับจะแสดงเป็นไฟล์ digital output. เกือบจะเทียบเท่ากับค่าอินพุตอะนาล็อกภายนอกที่เกี่ยวข้อง$V_{i}$.

ADC ประมาณต่อเนื่อง

ก successive approximation type ADC สร้างเอาต์พุตดิจิตอลซึ่งมีค่าประมาณเท่ากับอินพุตอะนาล็อกโดยใช้เทคนิคการประมาณค่าต่อเนื่องภายใน

block diagram ของ ADC โดยประมาณอย่างต่อเนื่องแสดงดังรูปต่อไปนี้

ADC การประมาณอย่างต่อเนื่องส่วนใหญ่ประกอบด้วยเครื่องกำเนิดสัญญาณนาฬิกา 5 บล็อก, การลงทะเบียนประมาณต่อเนื่อง (SAR), DAC, ตัวเปรียบเทียบและตรรกะการควบคุม

working ADC ประมาณต่อเนื่องมีดังนี้ -

control logic รีเซ็ตบิตทั้งหมดของ SAR และเปิดใช้งานเครื่องกำเนิดสัญญาณนาฬิกาเพื่อส่งพัลส์นาฬิกาไปยัง SAR เมื่อได้รับสัญญาณสั่งการเริ่มต้น
ข้อมูลไบนารี (ดิจิทัล) ที่มีอยู่ใน SARจะได้รับการอัปเดตสำหรับพัลส์นาฬิกาทุกครั้งตามเอาต์พุตของตัวเปรียบเทียบ เอาต์พุตของ SAR ถูกนำไปใช้เป็นอินพุตของ DAC
DAC แปลงอินพุตดิจิตอลที่ได้รับซึ่งเป็นเอาต์พุตของ SAR เป็นเอาต์พุตแบบอะนาล็อก ตัวเปรียบเทียบเปรียบเทียบค่าอะนาล็อกนี้$V_{a}$ ด้วยค่าอินพุตอะนาล็อกภายนอก $V_{i}$.
output of a comparator จะเป็น '1' ตราบเท่าที่ $V_{i}$ มากกว่า $V_{a}$. ในทำนองเดียวกันผลลัพธ์ของตัวเปรียบเทียบจะเป็น '0' เมื่อ$V_{i}$ น้อยกว่าหรือเท่ากับ $V_{a}$.
การดำเนินการที่กล่าวถึงในขั้นตอนข้างต้นจะดำเนินต่อไปจนกว่าเอาต์พุตดิจิทัลจะถูกต้อง

เอาต์พุตดิจิทัลจะเป็นเอาต์พุตที่ถูกต้องเมื่อเกือบเทียบเท่ากับค่าอินพุตอะนาล็อกภายนอกที่เกี่ยวข้อง $V_{i}$.

ประเภทแฟลช ADC

ก flash type ADCสร้างเอาต์พุตดิจิตอลที่เทียบเท่าสำหรับอินพุตอะนาล็อกที่สอดคล้องกันในเวลาไม่นาน ดังนั้น ADC ประเภทแฟลชจึงเป็น ADC ที่เร็วที่สุด

circuit diagram ADC ประเภทแฟลช 3 บิตแสดงดังรูปต่อไปนี้ -

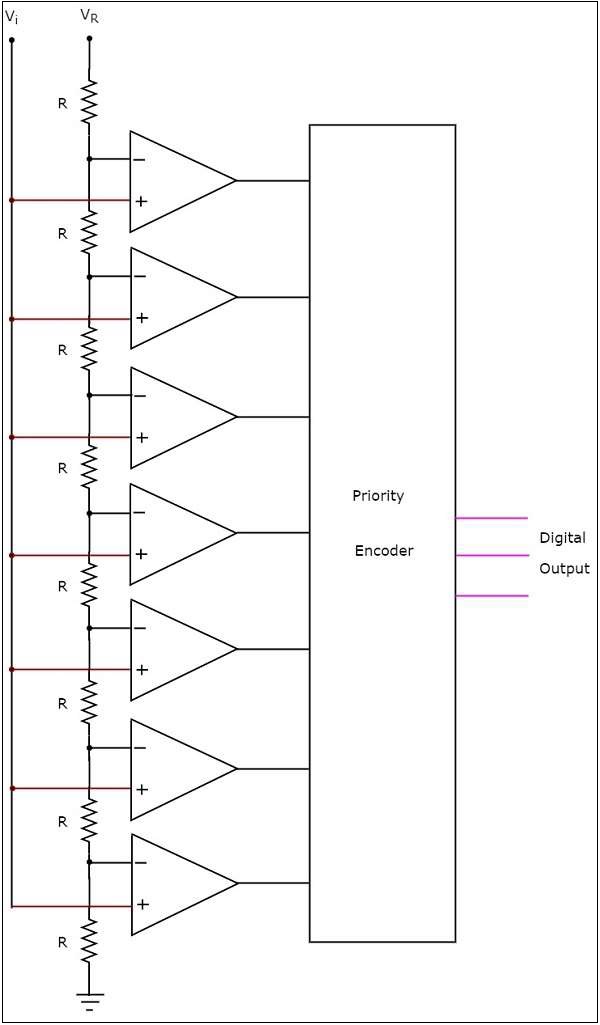
ADC ประเภทแฟลช 3 บิตประกอบด้วยเครือข่ายตัวแบ่งแรงดันไฟฟ้าตัวเปรียบเทียบ 7 ตัวและตัวเข้ารหัสลำดับความสำคัญ

working ADC ประเภทแฟลช 3 บิตมีดังนี้

voltage divider networkมีตัวต้านทานเท่ากัน 8 ตัว แรงดันไฟฟ้าอ้างอิง$V_{R}$ถูกนำไปใช้กับเครือข่ายทั้งหมดที่เกี่ยวกับภาคพื้นดิน แรงดันตกคร่อมตัวต้านทานแต่ละตัวจากล่างขึ้นบนเทียบกับกราวด์จะเป็นจำนวนเต็มทวีคูณ (ตั้งแต่ 1 ถึง 8) ของ$\frac{V_{R}}{8}$.
ภายนอก input voltage $V_{i}$ถูกนำไปใช้กับเทอร์มินัลที่ไม่กลับด้านของตัวเปรียบเทียบทั้งหมด แรงดันตกคร่อมตัวต้านทานแต่ละตัวจากล่างขึ้นบนเมื่อเทียบกับกราวด์ถูกนำไปใช้กับขั้วกลับด้านของเครื่องเปรียบเทียบจากล่างขึ้นบน
ในแต่ละครั้งเครื่องเปรียบเทียบทั้งหมดจะเปรียบเทียบแรงดันไฟฟ้าอินพุตภายนอกกับแรงดันไฟฟ้าที่ตกอยู่ที่ขั้วอินพุตอื่น ๆ ตามลำดับ นั่นหมายความว่าการดำเนินการเปรียบเทียบจะเกิดขึ้นโดยผู้เปรียบเทียบแต่ละคนparallelly.
output of the comparator จะเป็น '1' ตราบเท่าที่ $V_{i}$มากกว่าแรงดันตกที่ขั้วอินพุตอื่นตามลำดับ ในทำนองเดียวกันผลลัพธ์ของตัวเปรียบเทียบจะเป็น '0' เมื่อ$V_{i}$ มีค่าน้อยกว่าหรือเท่ากับแรงดันตกที่ขั้วอินพุตอื่นตามลำดับ
เอาต์พุตของตัวเปรียบเทียบทั้งหมดเชื่อมต่อเป็นอินพุตของ priority encoderตัวเข้ารหัสลำดับความสำคัญนี้สร้างรหัสไบนารี (เอาต์พุตดิจิทัล) ซึ่งสอดคล้องกับอินพุตที่มีลำดับความสำคัญสูงซึ่งมี '1'
ดังนั้นเอาต์พุตของตัวเข้ารหัสที่มีลำดับความสำคัญจึงไม่มีอะไรนอกจากการเทียบเท่าไบนารี (digital output) ของแรงดันไฟฟ้าอินพุตอะนาล็อกภายนอก $V_{i}$.

ADC ประเภทแฟลชใช้ในแอพพลิเคชั่นที่ความเร็วในการแปลงอินพุตอะนาล็อกเป็นข้อมูลดิจิทัลควรสูงมาก

ในบทที่แล้วเราได้กล่าวถึง ADC คืออะไรและตัวอย่างของ Direct type ADC บทนี้จะกล่าวถึง ADC ประเภททางอ้อม

หาก ADC ทำการแปลงอนาล็อกเป็นดิจิทัลโดยวิธีทางอ้อมจะเรียกว่าไฟล์ Indirect type ADC. โดยทั่วไปขั้นแรกจะแปลงอินพุตอะนาล็อกเป็นฟังก์ชันเชิงเส้นของเวลา (หรือความถี่) จากนั้นจะสร้างเอาต์พุตดิจิทัล (ไบนารี)

ADC ลาดชันคู่ดีที่สุด exampleของ ADC ประเภททางอ้อม ในบทนี้จะกล่าวถึงรายละเอียด

ADC แบบ Dual Slope

ตามชื่อคือก dual slope ADC สร้างเอาต์พุตดิจิตอลที่เทียบเท่ากันสำหรับอินพุตอะนาล็อกที่สอดคล้องกันโดยใช้เทคนิคความชันสอง (คู่)

block diagram ของ ADC แบบสองทางลาดแสดงในรูปต่อไปนี้ -

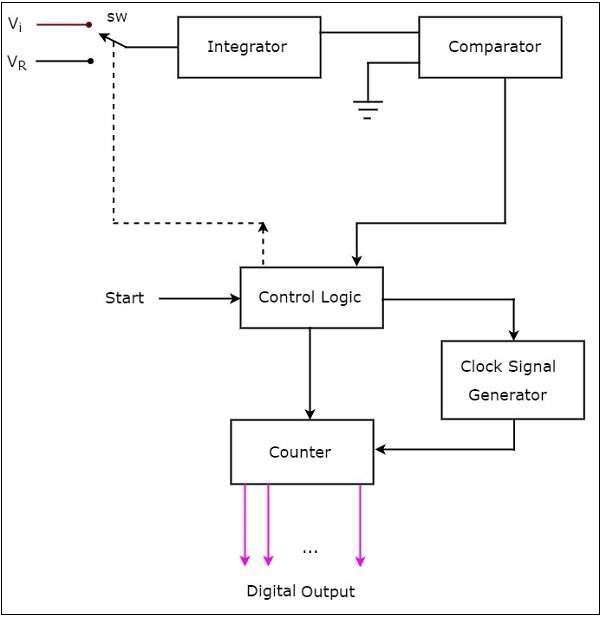
ADC แบบลาดคู่ส่วนใหญ่ประกอบด้วย 5 ช่วงตึก ได้แก่ Integrator, Comparator, Clock Signal Generator, Control Logic และ Counter

working ของ ADC แบบลาดชันคู่มีดังนี้ -

control logic รีเซ็ตตัวนับและเปิดใช้งานเครื่องกำเนิดสัญญาณนาฬิกาเพื่อส่งพัลส์นาฬิกาไปยังเคาน์เตอร์เมื่อได้รับสัญญาณสั่งการเริ่มต้น
ตรรกะการควบคุมจะผลักสวิตช์ sw เพื่อเชื่อมต่อกับไฟล์ external analog input voltage $V_{i}$เมื่อได้รับสัญญาณเริ่มสั่งการ แรงดันไฟฟ้าอินพุตนี้ใช้กับอินทิเกรเตอร์
ผลลัพธ์ของไฟล์ integrator เชื่อมต่อกับหนึ่งในสองอินพุตของตัวเปรียบเทียบและอินพุตอื่นของตัวเปรียบเทียบเชื่อมต่อกับกราวด์
Comparator เปรียบเทียบเอาต์พุตของอินทิเกรเตอร์กับศูนย์โวลต์ (กราวด์) และสร้างเอาต์พุตซึ่งใช้กับลอจิกควบคุม
counterได้รับการเพิ่มขึ้นทีละหนึ่งสำหรับพัลส์นาฬิกาทุกครั้งและค่าของมันจะอยู่ในรูปแบบไบนารี (ดิจิทัล) มันสร้างสัญญาณล้นไปยังตรรกะการควบคุมเมื่อมันเพิ่มขึ้นหลังจากถึงค่าการนับสูงสุด ในขณะนี้บิตของตัวนับทั้งหมดจะมีค่าเป็นศูนย์เท่านั้น
ตอนนี้ตรรกะการควบคุมจะผลักสวิตช์ sw เพื่อเชื่อมต่อกับไฟล์ negative reference แรงดันไฟฟ้า $-V_{ref}$. แรงดันอ้างอิงเชิงลบนี้ใช้กับอินทิเกรเตอร์ จะกำจัดประจุที่เก็บไว้ในตัวเก็บประจุออกจนกลายเป็นศูนย์
ในทันทีนี้อินพุตทั้งสองของตัวเปรียบเทียบมีโวลต์เป็นศูนย์ ดังนั้นตัวเปรียบเทียบจึงส่งสัญญาณไปยังตรรกะการควบคุม ตอนนี้ตรรกะการควบคุมจะปิดใช้งานตัวสร้างสัญญาณนาฬิกาและยังคง (ถือ) ค่าตัวนับ counter value เป็นสัดส่วนกับแรงดันไฟฟ้าอินพุตอะนาล็อกภายนอก
ในทันทีนี้ผลลัพธ์ของตัวนับจะแสดงเป็นไฟล์ digital output. เกือบจะเทียบเท่ากับค่าอินพุตอะนาล็อกภายนอกที่เกี่ยวข้อง$V_{i}$.

ADC แบบลาดคู่ใช้ในแอปพลิเคชันโดยที่ accuracy มีความสำคัญมากขึ้นในขณะที่แปลงอินพุตอะนาล็อกเป็นข้อมูลดิจิทัล (ไบนารี) ที่เทียบเท่า