MATLAB - บูรณาการ

การบูรณาการเกี่ยวข้องกับปัญหาสองประเภทที่แตกต่างกัน

ในประเภทแรกจะมีการกำหนดอนุพันธ์ของฟังก์ชันและเราต้องการค้นหาฟังก์ชัน ดังนั้นเราจึงย้อนกลับกระบวนการสร้างความแตกต่าง กระบวนการย้อนกลับนี้เรียกว่าการต่อต้านความแตกต่างหรือการค้นหาฟังก์ชันดั้งเดิมหรือการค้นหาindefinite integral.
ปัญหาประเภทที่สองเกี่ยวข้องกับการเพิ่มปริมาณที่น้อยมากเป็นจำนวนมากจากนั้นจึง จำกัด เมื่อขนาดของปริมาณเข้าใกล้ศูนย์ในขณะที่จำนวนคำมีแนวโน้มที่จะไม่มีที่สิ้นสุด กระบวนการนี้นำไปสู่คำจำกัดความของไฟล์definite integral.

อินทิกรัลที่แน่นอนใช้สำหรับการหาพื้นที่ปริมาตรจุดศูนย์ถ่วงโมเมนต์ความเฉื่อยงานที่ทำด้วยแรงและในการใช้งานอื่น ๆ อีกมากมาย

การค้นหาอินทิกรัลที่ไม่มีกำหนดโดยใช้ MATLAB

ตามนิยามถ้าอนุพันธ์ของฟังก์ชัน f (x) คือ f '(x) เราจะบอกว่าอินทิกรัลไม่ จำกัด ของ f' (x) เทียบกับ x คือ f (x) ยกตัวอย่างเช่นตั้งแต่อนุพันธ์ (ด้วยความเคารพ x) ของ x ²คือ 2x เราสามารถพูดได้ว่าหนึ่งไม่แน่นอนของ 2x คือ x 2

ในสัญลักษณ์ -

f'(x²) = 2xดังนั้น

∫ 2xdx = x².

อินทิกรัลไม่แน่นอนไม่ซ้ำกันเนื่องจากอนุพันธ์ของ x ² + c สำหรับค่าใด ๆ ของ c คงที่จะเป็น 2x ด้วย

สิ่งนี้แสดงในสัญลักษณ์เป็น -

∫ 2xdx = x² + c.

โดยที่ c เรียกว่า 'ค่าคงที่โดยพลการ'

MATLAB ให้ไฟล์ intคำสั่งสำหรับคำนวณอินทิกรัลของนิพจน์ เพื่อให้ได้นิพจน์สำหรับอินทิกรัลไม่ จำกัด ของฟังก์ชันเราเขียน -

int(f);

ตัวอย่างเช่นจากตัวอย่างก่อนหน้าของเรา -

syms x 
int(2*x)

MATLAB ดำเนินการคำสั่งข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -

ans =
   x^2

ตัวอย่าง 1

ในตัวอย่างนี้ให้เราหาอินทิกรัลของนิพจน์ที่ใช้กันทั่วไป สร้างไฟล์สคริปต์และพิมพ์รหัสต่อไปนี้ -

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

เมื่อคุณเรียกใช้ไฟล์จะแสดงผลลัพธ์ต่อไปนี้ -

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

ตัวอย่าง 2

สร้างไฟล์สคริปต์และพิมพ์รหัสต่อไปนี้ -

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))

int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))

int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

โปรดทราบว่าไฟล์ pretty ฟังก์ชันส่งคืนนิพจน์ในรูปแบบที่อ่านได้มากขึ้น

เมื่อคุณเรียกใช้ไฟล์จะแสดงผลลัพธ์ต่อไปนี้ -

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

การค้นหาอินทิกรัลที่แน่นอนโดยใช้ MATLAB

ตามความหมายแล้วอินทิกรัลที่แน่นอนคือขีด จำกัด ของผลรวม เราใช้ปริพันธ์ที่แน่นอนเพื่อหาพื้นที่เช่นพื้นที่ระหว่างเส้นโค้งกับแกน x และพื้นที่ระหว่างเส้นโค้งสองเส้น อินทิกรัลที่แน่นอนยังสามารถใช้ในสถานการณ์อื่น ๆ ซึ่งปริมาณที่ต้องการสามารถแสดงเป็นขีด จำกัด ของผลรวม

int ฟังก์ชันสามารถใช้สำหรับการรวมที่แน่นอนโดยส่งผ่านขีด จำกัด ที่คุณต้องการคำนวณอินทิกรัล

คำนวน

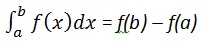
พวกเราเขียน,

int(x, a, b)

ตัวอย่างเช่นในการคำนวณค่าที่

เราเขียน -

int(x, 4, 9)

MATLAB ดำเนินการคำสั่งข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -

ans =
   65/2

ต่อไปนี้เป็น Octave เทียบเท่ากับการคำนวณข้างต้น -

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave รันโค้ดและส่งกลับผลลัพธ์ต่อไปนี้ -

Area: 

   32.500

โซลูชันทางเลือกสามารถกำหนดได้โดยใช้ฟังก์ชัน quad () ที่จัดทำโดย Octave ดังต่อไปนี้ -

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave รันโค้ดและส่งกลับผลลัพธ์ต่อไปนี้ -

Area: 
   32.500

ตัวอย่าง 1

ให้เราคำนวณพื้นที่ที่ล้อมรอบระหว่างแกน x และเส้นโค้ง y = x ³ −2x + 5 และพิกัด x = 1 และ x = 2

พื้นที่ที่ต้องการกำหนดโดย -

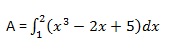
สร้างไฟล์สคริปต์และพิมพ์รหัสต่อไปนี้ -

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

เมื่อคุณเรียกใช้ไฟล์จะแสดงผลลัพธ์ต่อไปนี้ -

a =
23/4
Area: 
   5.7500

ต่อไปนี้เป็น Octave เทียบเท่ากับการคำนวณข้างต้น -

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave รันโค้ดและส่งกลับผลลัพธ์ต่อไปนี้ -

Area: 

   5.7500

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave รันโค้ดและส่งกลับผลลัพธ์ต่อไปนี้ -

Area: 
   5.7500

ตัวอย่าง 2

หาพื้นที่ใต้เส้นโค้ง: f (x) = x ² cos (x) สำหรับ −4 ≤ x ≤ 9

สร้างไฟล์สคริปต์และเขียนโค้ดต่อไปนี้ -

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

เมื่อคุณเรียกใช้ไฟล์ MATLAB จะลงจุดกราฟ -

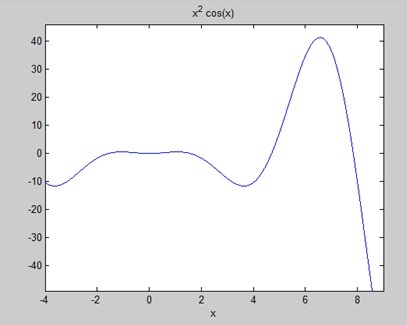
ผลลัพธ์จะได้รับด้านล่าง -

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

ต่อไปนี้เป็น Octave เทียบเท่ากับการคำนวณข้างต้น -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));