MATLAB - พหุนาม
MATLAB แทนพหุนามเป็นเวกเตอร์แถวที่มีค่าสัมประสิทธิ์เรียงลำดับตามกำลังจากมากไปหาน้อย ตัวอย่างเช่นสมการ P (x) = x 4 + 7x 3 - 5x + 9 สามารถแสดงเป็น -
p = [1 7 0 -5 9];
การประเมินพหุนาม
polyvalฟังก์ชันใช้สำหรับการประเมินพหุนามตามค่าที่ระบุ ตัวอย่างเช่นเพื่อประเมินพหุนามก่อนหน้าของเราp, ที่ x = 4, พิมพ์ -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB รันข้อความข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -
ans = 693MATLAB ยังมีไฟล์ polyvalmฟังก์ชันสำหรับการประเมินพหุนามเมทริกซ์ พหุนามเมทริกซ์คือpolynomial โดยมีเมทริกซ์เป็นตัวแปร
ตัวอย่างเช่นให้เราสร้างเมทริกซ์สี่เหลี่ยม X และประเมินพหุนาม p ที่ X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB รันข้อความข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269การหารากของพหุนาม
rootsฟังก์ชันคำนวณรากของพหุนาม ตัวอย่างเช่นในการคำนวณรากของพหุนาม p ของเราให้พิมพ์ -
p = [1 7 0 -5 9];
r = roots(p)MATLAB รันข้อความข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iฟังก์ชั่น polyเป็นค่าผกผันของฟังก์ชันรากและกลับไปที่สัมประสิทธิ์พหุนาม ตัวอย่างเช่น -
p2 = poly(r)MATLAB รันข้อความข้างต้นและส่งกลับผลลัพธ์ต่อไปนี้ -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iการติดตั้งเส้นโค้งพหุนาม
polyfitฟังก์ชันค้นหาค่าสัมประสิทธิ์ของพหุนามที่เหมาะกับชุดข้อมูลในความหมายกำลังสองน้อยที่สุด ถ้า x และ y เป็นเวกเตอร์สองตัวที่มีข้อมูล x และ y ที่จะพอดีกับพหุนามระดับ n เราจะได้พหุนามที่เหมาะสมกับข้อมูลโดยการเขียน -
p = polyfit(x,y,n)ตัวอย่าง
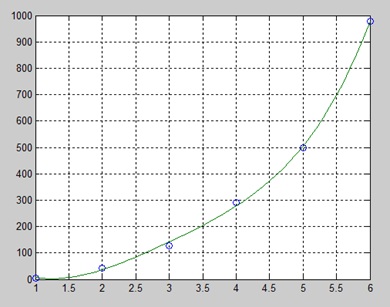
สร้างไฟล์สคริปต์และพิมพ์รหัสต่อไปนี้ -
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onเมื่อคุณเรียกใช้ไฟล์ MATLAB จะแสดงผลลัพธ์ต่อไปนี้ -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250และแปลงกราฟต่อไปนี้ -