Çizge Teorisi - Boyama
Grafik renklendirme, bazı kısıtlamalar altında köşeler, kenarlar ve bölgeler gibi grafik bileşenlerini etiketlemenin basit bir yolundan başka bir şey değildir. Bir grafikte, iki bitişik köşe, bitişik kenarlar veya bitişik bölgeler minimum sayıda renkle renklendirilmez. Bu numarayachromatic number ve grafiğin adı a properly colored graph.
Grafik renklendirirken, grafik üzerinde ayarlanan kısıtlamalar renkler, renklendirme sırası, renk atama şekli vb. Bir tepe noktasına veya belirli bir bölgeye renklendirme verilir. Böylece, aynı renkteki tepe noktaları veya bölgeler bağımsız kümeler oluşturur.
Köşe Renklendirme
Köşe renklendirme, iki bitişik köşe aynı renge sahip olmayacak şekilde bir 'G' grafiğinin köşelerine renklerin atanmasıdır. Basitçe söylemek gerekirse, bir kenarın iki köşesi aynı renkte olmamalıdır.
Kromatik Sayı
'G' grafiğinin köşe renklendirmesi için gereken minimum renk sayısı, X (G) ile gösterilen G'nin kromatik sayısı olarak adlandırılır.
χ (G) = 1 ancak ve ancak 'G' bir boş grafikse. 'G' boş bir grafik değilse, χ (G) ≥ 2.
Example
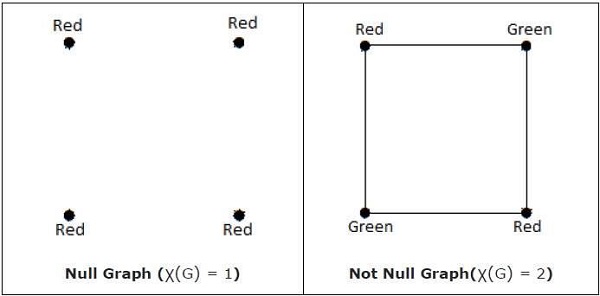
Note - En fazla n renk kullanan bir köşe renklendirmesi varsa, yani X (G) n ise, bir 'G' grafiğinin n-kaplanabilir olduğu söylenir.
Bölge Renklendirme
Bölge renklendirme, iki bitişik bölge aynı renge sahip olmayacak şekilde düzlemsel grafiğin bölgelerine renklerin atanmasıdır. Ortak bir kenara sahiplerse iki bölgenin bitişik olduğu söylenir.
Example
Aşağıdaki grafiğe bir göz atın. Bu iki bölge arasında ortak bir kenar 'be' olduğu için 'aeb' ve 'befc' bölgeleri bitişiktir.
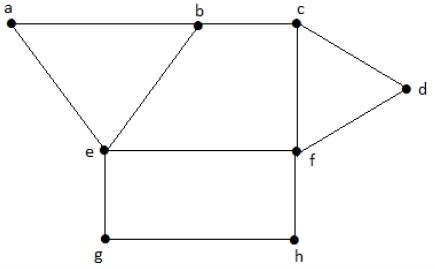
Benzer şekilde, diğer bölgeler de komşuluğa göre renklendirilir. Bu grafik aşağıdaki gibi renklendirilmiştir -
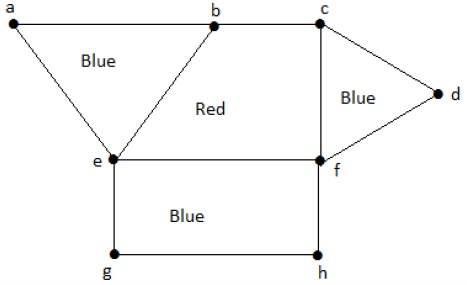
Example
Kn'in kromatik sayısı
- n
- n–1
- [n/2]
- [n/2]
Bu örneği K 4 ile düşünün .

Tam grafikte, her köşe, kalan (n - 1) köşelere bitişiktir. Bu nedenle, her köşe için yeni bir renk gerekir. Dolayısıyla kromatik sayı K n = n'dir.
Grafik Renklendirme Uygulamaları
Grafik renklendirme, grafik teorisindeki en önemli kavramlardan biridir. Bilgisayar biliminin birçok gerçek zamanlı uygulamasında kullanılır:
- Clustering
- Veri madenciliği
- Görüntü yakalama
- Resim parçalama
- Networking
- Kaynak tahsisi
- Süreç planlaması