Grafik Teorisi - Bağlantı
Bir grafiği bir tepe noktasından diğerine geçirmenin mümkün olup olmadığı, grafiğin nasıl bağlandığına göre belirlenir. Bağlantı, Grafik Teorisinde temel bir kavramdır. Bağlantı, bir grafiğin bağlı olup olmadığını tanımlar. Kenar bağlanabilirliği ve köşe bağlanabilirliği olarak bilinen, uç ve tepe noktasına dayalı alt konulara sahiptir. Bunları detaylı olarak tartışalım.
Bağlantı
Bir grafiğin olduğu söyleniyor connected if there is a path between every pair of vertex. Her bir tepe noktasından başka bir tepe noktasına kadar, geçmek için bir yol olmalıdır. Buna grafiğin bağlanabilirliği denir. Birden fazla bağlantısız köşe ve kenara sahip bir grafiğin bağlantısının kesildiği söyleniyor.
Example 1
Aşağıdaki grafikte, bir tepe noktasından başka herhangi bir tepe noktasına gitmek mümkündür. Örneğin, 'ab-e' yolunu kullanarak 'a' tepe noktasından 'e' tepe noktasına geçilebilir.
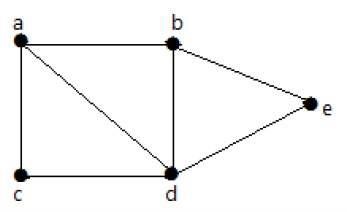
Example 2
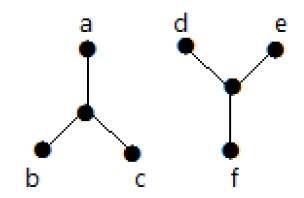
Aşağıdaki örnekte, 'a' tepe noktasından 'f' tepe noktasına geçmek mümkün değildir, çünkü aralarında doğrudan veya dolaylı yol yoktur. Dolayısıyla bağlantısız bir grafiktir.
Tepe Noktasını Kes
'G' bağlantılı bir grafik olsun. 'G-V' ('V'yi' G'den sil) bağlantısız bir grafikle sonuçlanırsa, bir V ∈ G tepe noktası 'G'nin kesik tepe noktası olarak adlandırılır. Bir grafikten kesilmiş bir tepe noktasını kaldırmak, onu iki veya daha fazla grafiğe böler.
Note - Kesilmiş bir tepe noktasının kaldırılması bir grafiğin bağlantısının kesilmesine neden olabilir.
Bağlı bir grafik 'G' en fazla (n – 2) kesik köşelere sahip olabilir.
Example
Aşağıdaki grafikte, 'e' ve 'c' köşeleri kesik köşelerdir.

"E" veya "c" yi kaldırarak, grafik bağlantısı kesilmiş bir grafik haline gelecektir.

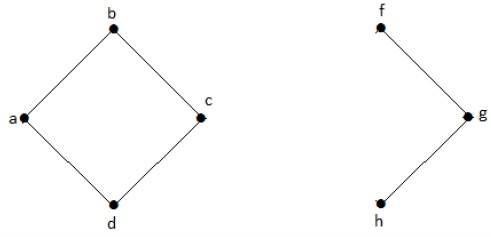
'G' olmadan, köşe 'c' ve köşe 'h' ve diğerleri arasında hiçbir yol yoktur. Bu nedenle, kesik tepe noktası 'e' olan bağlantısız bir grafiktir. Benzer şekilde, 'c' de yukarıdaki grafik için kesilmiş bir tepe noktasıdır.
Kesik Kenar (Köprü)
'G' bağlantılı bir grafik olsun. Bir 'e' ∈ G kenarı, 'G-e' bağlantısız bir grafikle sonuçlanırsa, kesik kenar olarak adlandırılır.
Bir grafikteki bir kenarı kaldırmak iki veya daha fazla grafikle sonuçlanıyorsa, bu kenara Kesik Kenar denir.
Example
Aşağıdaki grafikte kesme kenarı [(c, e)] 'dir.

Grafikten kenarı (c, e) kaldırarak bağlantısı kesilmiş bir grafiğe dönüşür.


Yukarıdaki grafikte, kenarı (c, e) kaldırmak, grafiği, bağlantısız bir grafikten başka bir şey olmayan ikiye böler. Bu nedenle, kenar (c, e) grafiğin kesik bir kenarıdır.
Note - 'G', 'n' köşeli bağlantılı bir grafik olsun, o zaman
bir kesme kenarı e ∈ G ancak ve ancak 'e' kenarı G'deki herhangi bir döngünün parçası değilse.
mümkün olan maksimum kesme kenarı sayısı "n-1" dir.
ne zaman kesik kenarlar varsa, kesik tepe noktaları da vardır çünkü kesilen kenarın en az bir tepe noktası kesik tepe noktasıdır.
bir kesik tepe mevcutsa, o zaman bir kesik kenar olabilir veya olmayabilir.
Bir Grafiğin Kesilmesi
'G' = (V, E) bağlantılı bir grafik olsun. E'nin tüm kenarlarının G'den silinmesi G'nin bağlantısını keserse, E'nin bir E 'alt kümesine G'nin bir kesik kümesi denir.
Bir grafikten belirli sayıda kenarın silinmesi bağlantısının kesilmesine neden oluyorsa, bu silinen kenarlara grafiğin kesim seti denir.
Example
Aşağıdaki grafiğe bir göz atın. Kesim seti E1 = {e1, e3, e5, e8} 'dir.
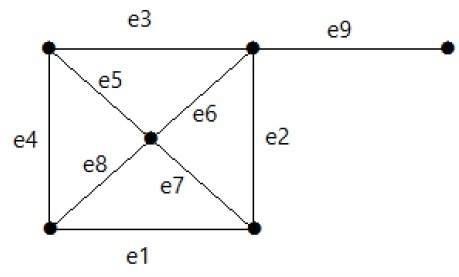
E1 kesim setini grafikten çıkardıktan sonra aşağıdaki gibi görünecektir -
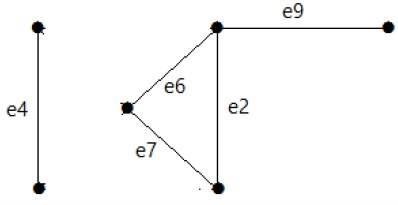
Benzer şekilde, grafiğin bağlantısını kesebilecek başka kesim setleri de vardır -
E3 = {e9} - Grafiğin en küçük kesim seti.
E4 = {e3, e4, e5}
Edge Bağlantısı
'G' bağlantılı bir grafik olsun. Kaldırılması "G" nin bağlantısını kesen minimum kenar sayısına G'nin kenar bağlanabilirliği denir.
Notation - λ (G)
Başka bir deyişle, number of edges in a smallest cut set of G G'nin kenar bağlantısı olarak adlandırılır.
'G'nin bir kesme kenarı varsa, λ (G) 1'dir (G'nin kenar bağlantısı)
Example
Aşağıdaki grafiğe bir göz atın. İki minimum kenarı kaldırarak, bağlı grafiğin bağlantısı kesilir. Dolayısıyla, kenar bağlantısı (λ (G)) 2'dir.
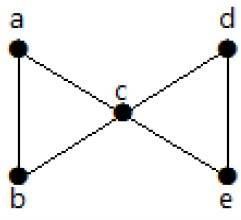
İki kenarı kaldırarak grafiğin bağlantısını kesmenin dört yolu:

Köşe Bağlantısı
'G' bağlantılı bir grafik olsun. Kaldırılmasıyla "G" nin bağlantısını kesen veya "G" yi önemsiz bir grafiğe indirgeyen minimum köşe noktası sayısına köşe bağlantısı denir.
Notation - K (G)
Example
Yukarıdaki grafikte, 'e' ve 'i' köşelerinin kaldırılması grafiğin bağlantısının kesilmesine neden olur.

G'nin kesilmiş bir tepe noktası varsa, K (G) = 1'dir.
Notation - Bağlı herhangi bir G grafiği için,
K (G) ≤ λ (G) ≤ δ (G)
Köşe bağlantısı (K (G)), kenar bağlantısı (λ (G)), minimum derece sayısı G (δ (G)).
Example
Aşağıdaki grafik için λ (G) ve K (G) 'yi hesaplayın -
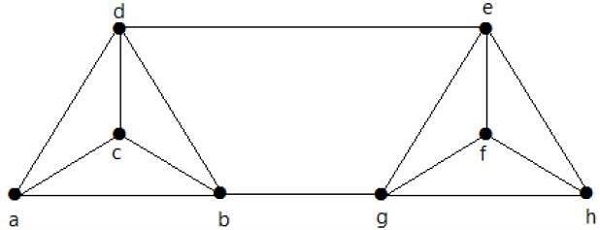
Solution
Grafikten
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
{D, e} ve {b, h} kenarlarını silerek, G'nin bağlantısını kesebiliriz.
Bu nedenle,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
(2) ve (3) 'den, köşe bağlantısı K (G) = 2