Çizge Teorisi - Kaplamalar

Kaplama grafiği, tüm köşeleri veya başka bir grafiğe karşılık gelen tüm kenarları içeren bir alt grafiktir. Tüm köşeleri içeren bir alt grafiğe aline/edge covering. Tüm kenarları içeren bir alt grafiğevertex covering.

Hat Kaplama

G = (V, E) bir grafik olsun. Bir alt kümeye C (E), G'nin her köşesinin C'deki en az bir kenarı ile karşılaşması durumunda G'nin bir çizgi örtmesi olarak adlandırılır

derece (V) ≥ 1 ∀ V ∈ G

çünkü her köşe, başka bir köşe ile bir kenarla bağlıdır. Bu nedenle minimum 1 derecesine sahiptir.

Example

Aşağıdaki grafiğe bir göz atın -

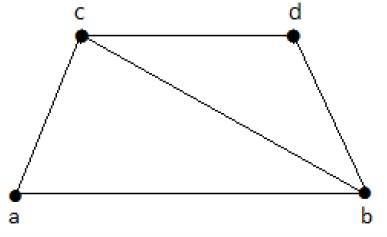
Hat örtüsüne sahip alt grafikleri aşağıdaki gibidir:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

"G" nin satır kaplaması, ancak ve ancak "G" izole bir tepe noktasına sahipse mevcut değildir. "N" köşeli bir grafiğin çizgi kaplamasının en az [n / 2] kenarı vardır.

Minimal Hat Kaplaması

Bir G grafiğinin C'sini kapsayan bir çizginin minimum olduğu söylenir if no edge can be deleted from C.

Example

Yukarıdaki grafikte, çizgi kaplamasına sahip alt grafikler aşağıdaki gibidir -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Burada, C ₁ , C ₂ , C ₃ minimal satır kaplamalarıdır, C ₄ ise {b, c} 'yi silebildiğimiz için değildir.

Minimum Hat Kaplaması

Olarak da bilinir Smallest Minimal Line Covering. Minimum sayıda kenarlı minimum çizgi örtme, minimum 'G' çizgi kaplaması olarak adlandırılır. 'G'yi kapsayan minimum bir çizgideki kenarların sayısı,line covering number'G' (α ₁ ).

Example

Yukarıdaki örnekte, C ₁ ve C ₂ , G ve α ₁ = 2'nin minimum çizgi kaplamasıdır .

Her hat kaplaması, minimum bir çizgi kaplaması içerir.
Her hat örtme minimum çizgi örtme içermemektedir (C ₃ herhangi bir minimum çizgi örtme içermemektedir.
Asgari hat kaplaması bir döngü içermez.
"C" yi kapsayan bir çizgi 3 veya daha fazla uzunlukta yol içermiyorsa, "C" minimum çizgiyi kaplar çünkü "C" nin tüm bileşenleri yıldız grafiğidir ve bir yıldız grafiğinden hiçbir kenar silinemez.

Köşe Kaplaması

'G' = (V, E) bir grafik olsun. V'nin bir K alt kümesine, "G" nin her kenarı "K" da bir tepe noktasıyla karşılaşıyorsa veya bununla kaplıysa, "G" nin köşe kaplaması olarak adlandırılır.

Example

Aşağıdaki grafiğe bir göz atın -

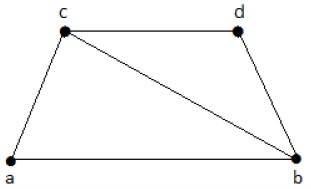
Yukarıdaki grafikten türetilebilecek alt grafikler aşağıdaki gibidir -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

Burada, K ₁ , K ₂ ve K ₃ tepe örtüsüne sahipken, K ₄ kenarı {bc} örtmediği için herhangi bir tepe kaplamasına sahip değildir.

Minimum Köşe Kaplaması

'G' grafiğinin bir köşe 'K', 'K' noktasından hiçbir köşe silinemezse, minimum köşe kaplaması olduğu söylenir.

Example

Yukarıdaki grafikte, köşe kaplamasına sahip alt grafikler aşağıdaki gibidir -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Burada, K ₁ ve K ₂ minimum köşe kaplamalarıdır, oysa K _3'te köşe 'd' silinebilir.

Minimum Köşe Kaplaması

Aynı zamanda en küçük minimal köşe kaplaması olarak da bilinir. Minimum sayıda köşeli 'G' grafiğinin minimum köşe kaplaması, minimum köşe kaplaması olarak adlandırılır.

'G' nin minimum köşe kaplamasındaki köşe noktalarının sayısına, köşe kaplama sayısı G (α ₂ ) denir .

Example

Aşağıdaki grafikte, köşe kaplamasına sahip alt grafikler aşağıdaki gibidir -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}