Çizge Teorisi - İzomorfizm
Bir grafik aynı sayıda köşeye, kenara ve aynı zamanda aynı kenar bağlantısına sahip farklı formlarda mevcut olabilir. Bu tür grafiklere izomorfik grafikler denir. Bu bölümdeki grafikleri esas olarak bunlara atıfta bulunmak ve birbirlerinden tanımak amacıyla etiketlediğimize dikkat edin.
İzomorfik Grafikler
İki G 1 ve G 2 grafiğinin izomorf olduğu söylenir - eğer -
Bileşen sayısı (köşeler ve kenarlar) aynıdır.
Uç bağlantıları korunur.
Note- Kısacası, iki izomorfik grafikten biri diğerinin ince ayarlı versiyonu. Etiketsiz bir grafik, izomorfik bir grafik olarak da düşünülebilir.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
G 1 ≡ G 2 ise o zaman -
| V (G 1 ) | = | V (G 2 ) |
| E (G 1 ) | = | E (G 2 ) |
G 1 ve G 2'nin derece dizileri aynıdır.
{V 1 , V 2 , .. Vk} köşeleri G 1'de K uzunluğunda bir döngü oluşturuyorsa , {f (V 1 ), f (V 2 ),… f (Vk)} köşeleri bir döngü oluşturmalıdır G 2 cinsinden K uzunluğunda .
Yukarıdaki koşulların tümü, G 1 ve G 2 grafiklerinin izomorfik olması için gereklidir, ancak grafiklerin izomorfik olduğunu kanıtlamak için yeterli değildir.
(G 1 ≡ G 2 ) ancak ve ancak (G 1 - ≡ G 2 -) burada G 1 ve G 2 basit grafiklerdir.
(G 1 ≡ G 2 ) G 1 ve G 2'nin bitişik matrisleri aynıysa.
(G 1 ≡ G 2 ) ancak ve ancak G 1 ve G 2'nin karşılık gelen alt grafikleri (G1'deki bazı köşeler ve bunların grafik G 2'deki görüntüleri silinerek elde edilmiştir ) izomorfik ise.
Example
Aşağıdaki grafiklerden hangisi izomorfiktir?
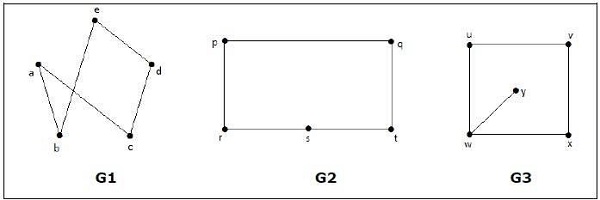
G 3 grafiğinde , köşe 'w' yalnızca derece 3'e sahipken, diğer tüm grafik köşeleri 2. dereceye sahiptir. Dolayısıyla G3, G 1 veya G 2'ye izomorfik değildir .
G 1 ve G 2'yi tamamlayarak, sahip olduğunuz -
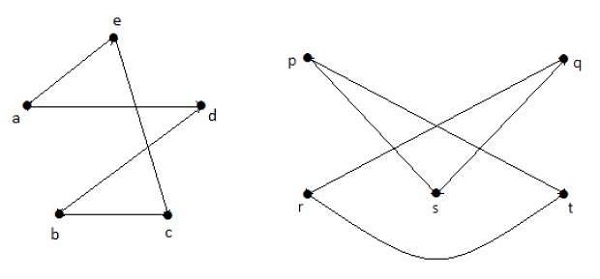
Burada, (G 1 - ≡ G 2 -), dolayısıyla (G 1 ≡ G 2 ).
Düzlemsel Grafikler
Bir 'G' grafiğinin, bir düzlem veya küre üzerinde çizilebiliyorsa, iki kenarın tepe noktası olmayan bir noktada birbiriyle kesişmemesi için düzlemsel olduğu söylenir.
Example
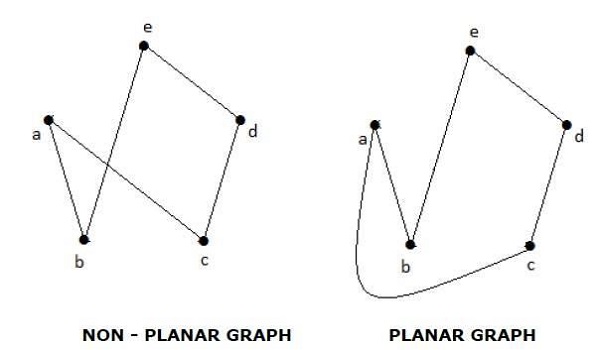
Bölgeler
Her düzlemsel grafik, düzlemi bölgeler adı verilen bağlantılı alanlara böler.
Example
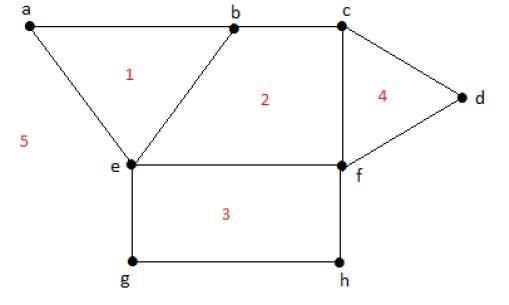
Sınırlı bir bölgenin derecesi r = deg(r) = Bölgeleri çevreleyen kenar sayısı r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8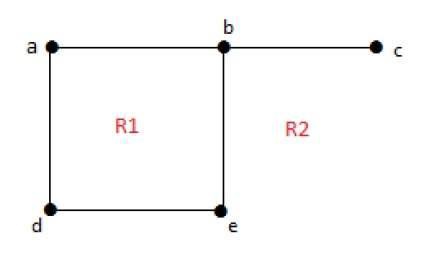
Sınırsız bir bölgenin derecesi r = deg(r) = Bölgeleri çevreleyen kenar sayısı r.
deg(R1) = 4
deg(R2) = 6Düzlemsel grafiklerde aşağıdaki özellikler iyidir -
'N' köşeli düzlemsel bir grafikte, tüm köşelerin derecelerinin toplamı -
Göre Sum of Degrees of Regions/ Teorem, 'n' bölgeli düzlemsel bir grafikte, bölgelerin derece toplamı -
Yukarıdaki teoreme dayanarak, aşağıdaki sonuçları çıkarabilirsiniz -
Düzlemsel bir grafikte,
Her bölgenin derecesi K ise, bölgelerin derecelerinin toplamı -
Her bölgenin derecesi en az K (≥ K) ise, o zaman
Her bölgenin derecesi en fazla K (≤ K) ise, o zaman
Note - Tüm bölgelerin aynı dereceye sahip olduğunu varsayalım.
Göre Euler’s Formulae düzlemsel grafiklerde,
Bir 'G' grafiği bağlantılı bir düzlemsel ise, o zaman
'K' bileşenli bir düzlemsel grafik ise,
Nerede, | V | köşe sayısıdır, | E | kenar sayısıdır ve | R | bölge sayısıdır.
Edge Vertex Eşitsizliği
'G', her bölgenin derecesi en az 'K' olan bağlantılı bir düzlemsel grafikse, o zaman,
| E | ≤ k / (k-2) {| v | - 2}
Biliyorsun, | V | + | R | = | E | + 2
K. | R | ≤ 2 | E |
K (| E | - | V | + 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
| E | ≤ k / (k-2) {| v | - 2}
'G' basit bir bağlantılı düzlemsel grafikse,
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4Deg (V) ≤ 5 olacak şekilde en az bir V • ∈ G tepe noktası vardır.
'G' basit bağlantılı bir düzlemsel grafikse (en az 2 kenarlı) ve üçgen yoksa, o zaman
|E| ≤ {2|V| – 4}Kuratowski Teoremi
Bir grafik 'G', düzlemsel olmayan ise ve G '' K homeomorphic bir alt grafiğini sahip olması durumunda 5 ya da K 3,3 .
Homomorfizm
G 1 ve G 2 grafiğinin homomorfik olduğu söylenir, eğer bu grafiklerin her biri G'nin bazı kenarlarını daha fazla köşeye bölerek aynı 'G' grafiğinden elde edilebilir. Aşağıdaki örneğe bir göz atın -

Bir köşe ekleyerek 'rs' kenarını iki kenara bölün.
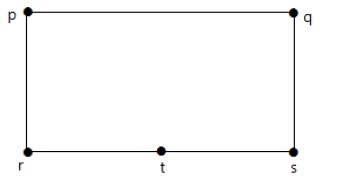
Aşağıda gösterilen grafikler ilk grafiğe homomorfiktir.
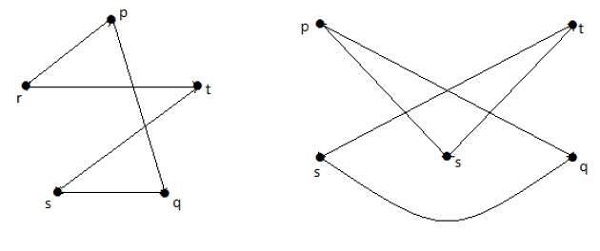
G ise 1 G izomorf 2 , daha sonra G G2 homeomorphic fakat tersi ihtiyaç doğru olmayabilir.
4 veya daha az köşeli herhangi bir grafik düzlemseldir.
8 veya daha az kenarlı herhangi bir grafik düzlemseldir.
Tam bir K n grafiği ancak ve ancak n ≤ 4 ise düzlemseldir.
Tam iki taraflı grafik K m, n , ancak ve ancak m ≤ 2 veya n ≤ 2 ise düzlemseldir.
Minimum sayıda köşeye sahip basit bir düzlemsel olmayan grafik, K 5 grafiğidir .
Minimum kenar sayısına sahip basit düzlemsel olmayan grafik K 3, 3'tür .
Çok yüzlü grafik
Basit bir bağlantılı düzlemsel grafiğe çokyüzlü grafik denir, eğer her bir tepe noktasının derecesi ≥ 3 ise, yani derece (V) ≥ 3 ∀ V ∈ G.
3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |