Çizge Teorisi - Örnekler
Bu bölümde, daha önceki bölümlerde tartıştığımız kavramları göstermek için birkaç standart örneği ele alacağız.
örnek 1
Find the number of spanning trees in the following graph.
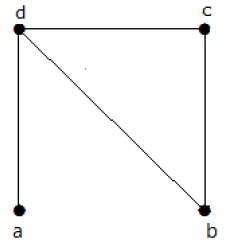
Çözüm
Yukarıdaki grafikten elde edilen yayılan ağaç sayısı 3'tür. Bunlar aşağıdaki gibidir -
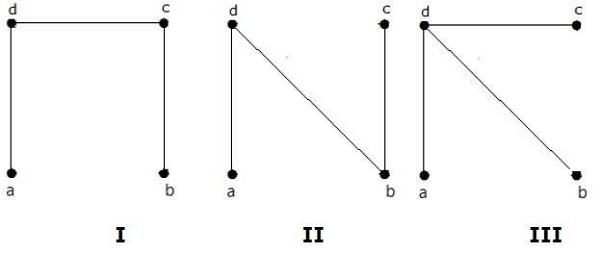
Bu üç, verilen grafikler için uzanan ağaçlardır. Burada I ve II grafikleri birbirine izomorftur. Açıkça, izomorfik olmayan yayılan ağaçların sayısı ikidir.
Örnek 2
How many simple non-isomorphic graphs are possible with 3 vertices?
Çözüm
3 köşeli 4 izomorfik olmayan grafik mümkündür. Aşağıda gösterilmiştir.
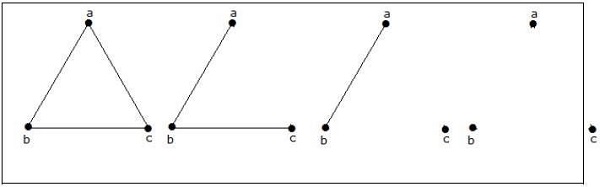
Örnek 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Çözüm
Derece teoreminin toplamına göre,
20 Σ i = 1 derece (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Euler'in formülüne göre,
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Dolayısıyla bölge sayısı 12'dir.
Örnek 4
What is the chromatic number of complete graph Kn?
Çözüm
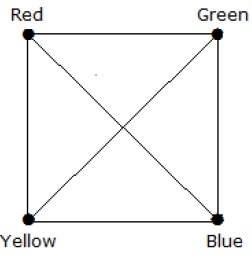
Tam bir grafikte, her köşe, kalan (n – 1) köşelere bitişiktir. Bu nedenle, her köşe için yeni bir renk gerekir. Dolayısıyla kromatik sayı K n = n.
Örnek 5
What is the matching number for the following graph?
Çözüm
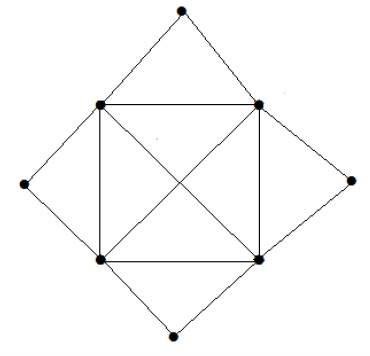
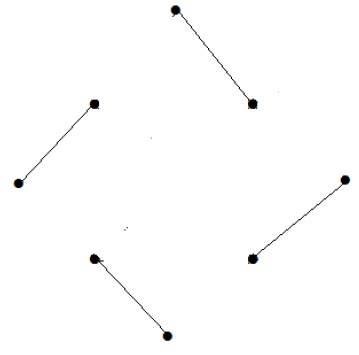
Köşe sayısı = 9
Yalnızca 8 köşeyi eşleştirebiliriz.
Eşleşen numara 4'tür.
Örnek 6
What is the line covering number of for the following graph?
Çözüm
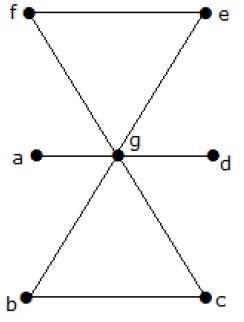
Köşe sayısı = | V | = n = 7
Satır kaplama sayısı = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
3 kenar kullanarak tüm köşeleri kapatabiliriz.
Dolayısıyla satır kaplama numarası 3'tür.