Çizge Teorisi - Bağımsız Kümeler

Bağımsız kümeler, kümeler halinde temsil edilir.

• olmamalı any edges adjacent to each other. Herhangi iki kenar arasında herhangi bir ortak tepe olmamalıdır.

• olmamalı any vertices adjacent to each other. Herhangi iki köşe arasında herhangi bir ortak kenar olmamalıdır.

Bağımsız Hat Seti

'G' = (V, E) bir grafik olsun. L'deki iki kenar bitişik değilse, E'nin bir alt kümesi bağımsız bir 'G' çizgi kümesi olarak adlandırılır. Böyle bir kümeye bağımsız bir çizgi kümesi denir.

Example

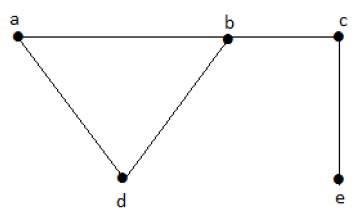
Aşağıdaki alt kümeleri ele alalım -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

Bu örnekte, L2 ve L3 alt kümeleri, verilen grafikte açıkça bitişik kenarlar değildir. Bağımsız çizgi kümeleridir. Ancak L1 bağımsız bir çizgi seti değildir, bağımsız bir çizgi seti yapmak için en az iki kenar olmalıdır.

Maksimal Bağımsız Hat Seti

"L" ye başka bir "G" kenarı eklenemiyorsa, bağımsız bir çizgi kümesinin bir grafiğin "G" maksimum bağımsız çizgi kümesi olduğu söylenir.

Example

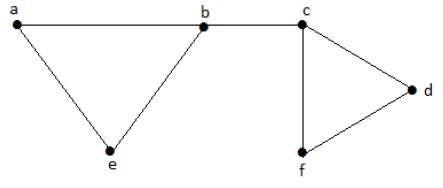
Aşağıdaki alt kümeleri ele alalım -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ ve L ₃ , maksimum bağımsız çizgi kümeleridir / maksimum eşleşmedir. Yalnızca bu iki alt kümeye gelince, bitişik olmayan başka bir kenar ekleme şansı yoktur. Bu nedenle bu iki alt küme, maksimum bağımsız çizgi kümeleri olarak kabul edilir.

Maksimum Bağımsız Hat Seti

Maksimum sayıda kenara sahip maksimum bağımsız "G" çizgi kümesi, maksimum bağımsız "G" çizgi kümesi olarak adlandırılır.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

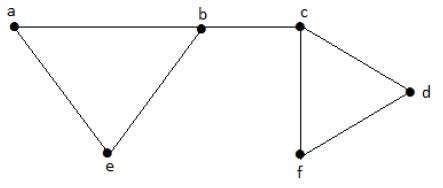
Aşağıdaki alt kümeleri ele alalım -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ , grafikte bitişik kenarlar olmayan ve β1 = 3 ile gösterilen maksimum kenarlara sahip maksimum bağımsız G çizgi kümesidir.

Note - İzole tepe noktası olmayan herhangi bir G grafiği için,

α1 + β1 = bir grafikteki köşe sayısı = | V |

Example

K _n / C _n / w _n sayısını kapsayan hat ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {case} \ frac {n} {2} \: if \: n \: eşittir \: eşittir \\\ frac {n + 1} {2} \: eğer \: n \: eşittir \: tek \ end {durum} $$

Satırdan bağımsız sayı (Eşleşen sayı) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Bağımsız Köşe Kümesi

'G' = (V, E) bir grafik olsun. "S" deki iki köşe bitişik değilse, "V" nin bir alt kümesi bağımsız bir "G" kümesi olarak adlandırılır.

Example

Yukarıdaki grafiklerden aşağıdaki alt kümeleri düşünün -

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Açıkça S ₁ bağımsız bir köşe kümesi değildir, çünkü bağımsız bir köşe seti elde etmek için bir grafikten en az iki köşe olmalıdır. Ama burada durum bu değil. Alt-gruplar G ₂ , S ₃ , S ₄ alt kümelerinden herhangi bir tepe bitişik olan bir tepe bulunmayacağım çünkü bağımsız tepe kümeleridir.

Maksimal Bağımsız Köşe Kümesi

'G' bir grafik olsun, o zaman bağımsız bir 'G' köşe kümesinin, 'S'ye başka bir' G 'tepe noktası eklenemiyorsa maksimum olduğu söylenir.

Example

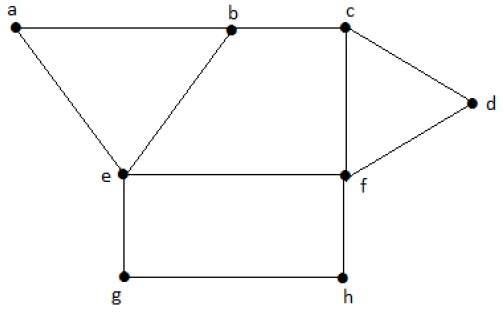
Yukarıdaki grafiklerden aşağıdaki alt kümeleri düşünün.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ ve S ₃ 'G' maksimal bağımsız tepe kümeleridir. S ₁ ve S _4'te başka köşeler ekleyebiliriz; fakat S ₂ ve S ₃ , herhangi bir başka köşe ekleyemezsiniz.

Maksimum Bağımsız Köşe Kümesi

Maksimum sayıda köşe noktasına sahip maksimum bağımsız köşe kümesi 'G', maksimum bağımsız köşe kümesi olarak adlandırılır.

Example

Yukarıdaki grafikten aşağıdaki alt kümeleri düşünün -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Yalnızca S ₃ , en yüksek sayıda köşeyi kapsadığı için maksimum bağımsız köşe kümesidir. 'G'nin maksimum bağımsız köşe kümesindeki köşe noktalarının sayısına bağımsız köşe sayısı G (β ₂ ) denir .

Example

Tam grafik K _{n için} ,

Köşe kaplama sayısı = α ₂ = n − 1

Köşe bağımsız sayı = β ₂ = 1

Α ₂ + β ₂ = n'ye sahipsiniz

Tam bir grafikte, her köşe, kalan (n - 1) köşelerine bitişiktir. Bu nedenle, maksimum bağımsız bir K _n kümesi yalnızca bir köşe içerir.

Bu nedenle, β ₂ = 1

ve α ₂ = | v | - β ₂ = n-1

Note - Herhangi bir 'G' = (V, E) grafiği için

• α ₂ + β ₂ = | v |
• "S" bağımsız bir köşe kümesi "G" ise, (V - S) G'nin köşe kaplamasıdır.