Grafik Teorisi - Hızlı Kılavuz

Matematik ve bilgisayar bilimi alanında, grafik teorisi, kenarlar ve köşeler arasındaki ilişkiyle ilgilenen grafiklerin incelenmesidir . Birkaç isim vermek gerekirse bilgisayar bilimi, bilgi teknolojisi, biyobilimler, matematik ve dilbilimde uygulamaları olan popüler bir konudur. Daha fazla uzatmadan, bir grafik tanımlayarak başlayalım.

Grafik nedir?

Grafik, bazı nesne çiftlerinin bağlantılarla birbirine bağlandığı bir dizi nesnenin resimli bir temsilidir. Birbirine bağlı nesneler olarak adlandırılan noktalarla temsil edilirverticesve köşeleri birbirine bağlayan bağlantılara edges.

Resmi olarak, bir grafik bir çift settir (V, E), nerede Vköşeler kümesidir ve E, köşe çiftlerini birbirine bağlayan kenarlar kümesidir. Aşağıdaki grafiğe bir göz atın -

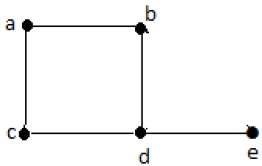
Yukarıdaki grafikte,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Çizge Teorisinin Uygulamaları

Grafik teorisinin çeşitli mühendislik alanlarında uygulamaları vardır -

Electrical Engineering- Grafik teorisi kavramları, devre bağlantılarının tasarımında yaygın olarak kullanılır. Bağlantı türleri veya organizasyonu topolojiler olarak adlandırılır. Topolojiler için bazı örnekler yıldız, köprü, seri ve paralel topolojilerdir.

Computer Science- Algoritmaların incelenmesi için grafik teorisi kullanılır. Örneğin,

• Kruskal Algoritması
• Prim Algoritması
• Dijkstra Algoritması

Computer Network - Ağdaki birbirine bağlı bilgisayarlar arasındaki ilişkiler, grafik teorisinin ilkelerini izler.

Science - Bir maddenin moleküler yapısı ve kimyasal yapısı, bir organizmanın DNA yapısı vb. Grafiklerle temsil edilir.

Linguistics - Bir dilin ayrıştırma ağacı ve bir dilin grameri grafikler kullanır.

General- Şehirler arası güzergahlar grafiklerle gösterilebilir. Soy ağacı gibi hiyerarşik sıralı bilgileri gösteren, ağaç adı verilen özel bir grafik türü olarak kullanılabilir.

Grafik, noktalara bağlı noktaların ve çizgilerin diyagramıdır. Kendisini birbirine bağlayan tepe noktası olmayan iki tepe noktasını birleştiren en az bir çizgiye sahiptir. Grafik teorisindeki grafik kavramı, nokta, çizgi, tepe noktası, kenar, köşe dereceleri, grafiklerin özellikleri, vb. Gibi bazı temel terimler üzerinde durmaktadır. Burada, bu bölümde, grafik teorisinin bu temellerini ele alacağız.

Nokta

A pointtek boyutlu, iki boyutlu veya üç boyutlu bir uzayda belirli bir konumdur. Daha iyi anlamak için bir nokta bir alfabe ile gösterilebilir. Bir nokta ile temsil edilebilir.

Misal

Burada nokta, 'a' adlı bir noktadır.

Hat

Bir Lineiki nokta arasındaki bir bağlantıdır. Düz bir çizgi ile temsil edilebilir.

Example

Burada 'a' ve 'b' noktalardır. Bu iki nokta arasındaki bağlantıya doğru denir.

Köşe

Köşe, birden çok çizginin kesiştiği noktadır. Aynı zamanda anode. Noktalara benzer şekilde, bir tepe noktası da bir alfabe ile gösterilir.

Example

Burada tepe noktası bir 'a' alfabesiyle adlandırılır.

Kenar

Kenar, iki köşeyi birbirine bağlayan bir çizginin matematiksel terimidir. Tek bir tepe noktasından birçok kenar oluşturulabilir. Bir tepe noktası olmadan kenar oluşturulamaz. Bir kenar için bir başlangıç ​​tepe noktası ve bir bitiş tepe noktası olmalıdır.

Example

Burada, 'a' ve 'b' iki köşedir ve aralarındaki bağlantıya kenar adı verilir.

Grafik

Bir 'G' grafiği, G = (V, E) olarak tanımlanır. Burada V, tüm köşelerin bir kümesidir ve E, grafikteki tüm kenarların bir kümesidir.

Example 1

Yukarıdaki örnekte, ab, ac, cd ve bd grafiğin kenarlarıdır. Benzer şekilde, a, b, c ve d grafiğin köşeleridir.

Example 2

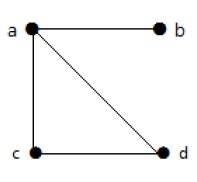
Bu grafikte dört köşe a, b, c ve d ve dört kenar ab, ac, ad ve cd vardır.

Döngü

Bir grafikte, tepe noktasından kendisine bir kenar çizilirse, buna döngü denir.

Example 1

Yukarıdaki grafikte, V, kendisi için bir döngü oluşturan bir kenarı (V, V) olan bir tepe noktasıdır.

Example 2

Bu grafikte, tepe a ve tepe b'de oluşan iki döngü vardır.

Köşe Derecesi

Bir tepe V'ye bitişik köşelerin sayısıdır.

Notation - derece (V).

N sayıda köşeli basit bir grafikte, herhangi bir köşenin derecesi -

derece (v) ≤ n - 1 ∀ v ∈ G

Bir köşe, kendisi dışında diğer tüm köşelerle bir kenar oluşturabilir. Yani bir tepe noktası derecesi,number of vertices in the graph minus 1. Bu 1, kendi başına bir döngü oluşturamayacağı için öz tepe içindir. Herhangi bir köşede döngü varsa, bu Basit Grafik değildir.

Köşe derecesi iki grafik durumu altında düşünülebilir -

• Yönlendirilmemiş Grafik

• Yönlendirilmiş grafik

Yönlendirilmemiş Grafikteki Köşe Derecesi

Yönlendirilmemiş bir grafiğin yönlendirilmiş kenarları yoktur. Aşağıdaki örnekleri düşünün.

Example 1

Aşağıdaki grafiğe bir göz atın -

Yukarıdaki Yönlendirilmemiş Grafikte,

• deg (a) = 2, çünkü 'a' tepe noktasında buluşan 2 kenar var.

• derece (b) = 3, çünkü 'b' tepe noktasında buluşan 3 kenar var.

• deg (c) = 1, çünkü 'c' tepe noktasında 1 kenar oluşmuştur

• Yani 'c' bir pendent vertex.

• deg (d) = 2, çünkü 'd' tepe noktasında buluşan 2 kenar vardır.

• deg (e) = 0, çünkü 'e' tepe noktasında 0 kenar oluşmuştur.

• Yani 'e' bir isolated vertex.

Example 2

Aşağıdaki grafiğe bir göz atın -

Yukarıdaki grafikte,

derece (a) = 2, derece (b) = 2, derece (c) = 2, derece (d) = 2 ve derece (e) = 0.

Tepe 'e' izole edilmiş bir tepe noktasıdır. Grafiğin sarkık tepe noktası yoktur.

Yönlendirilmiş Grafikte Köşe Derecesi

Yönlendirilmiş bir grafikte, her tepe noktasının bir indegree ve bir outdegree.

Grafik Derecesi

• V tepe noktası, tepe V'ye gelen kenarların sayısıdır.

• Notation - derece (V).

Bir Grafiğin Olağanüstü Derecesi

• Tepe V'nin dış derecesi, tepe V'den çıkan kenarların sayısıdır.

• Notation - derece + (V).

Aşağıdaki örnekleri düşünün.

Example 1

Aşağıdaki yönlendirilmiş grafiğe bir göz atın. Köşe "a" nın iki kenarı vardır, "ad" ve "ab", dışa doğru gitmektedir. Dolayısıyla dış derecesi 2'dir. Benzer şekilde, "a" tepe noktasına doğru gelen bir kenar "ga" vardır. Dolayısıyla "a" nın belirsizliği 1'dir.

Diğer köşelerin belirsizliği ve derecesi aşağıdaki tabloda gösterilmektedir -

Köşe	Indegree	Outdegree
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

Example 2

Aşağıdaki yönlendirilmiş grafiğe bir göz atın. Köşe 'a', köşe 'a' dan dışarıya doğru giden bir kenar 'ae'ye sahiptir. Dolayısıyla, dış derecesi 1'dir. Benzer şekilde, grafikte 'a' tepe noktasına doğru gelen bir 'ba' kenarı vardır. Dolayısıyla "a" nın belirsizliği 1'dir.

Diğer köşelerin belirsizliği ve derecesi aşağıdaki tabloda gösterilmektedir -

Köşe	Indegree	Outdegree
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

Sarkık Köşe

Bir tepe noktasının derecesini kullanarak, iki özel köşe türüne sahibiz. Birinci derece olan bir tepe noktasına asılı köşe denir.

Example

Burada, bu örnekte köşe 'a' ve köşe 'b' bağlantılı bir kenara 'ab' sahiptir. Dolayısıyla, 'a' tepe noktasına göre, 'b' tepe noktasına doğru sadece bir kenar vardır ve 'b' tepe noktasına göre benzer şekilde, 'a' tepe noktasına doğru sadece bir kenar vardır. Son olarak, köşe 'a' ve köşe 'b', aynı zamanda asılı köşe olarak da adlandırılan bir dereceye sahiptir.

İzole Köşe

Sıfır dereceli bir tepe noktasına izole tepe noktası denir.

Example

Burada, köşe 'a' ve köşe 'b' birbirleri arasında ve ayrıca diğer köşelerle bağlantıya sahip değildir. Yani hem 'a' hem de 'b' köşelerinin derecesi sıfırdır. Bunlara ayrıca izole köşeler denir.

Bitişiklik

İşte bitişiklik normları -

• Bir grafikte iki köşe olduğu söylenir adjacent, iki köşe arasında bir kenar varsa. Burada, köşelerin bitişikliği, bu iki köşeyi birleştiren tek kenar tarafından korunur.

• Bir grafikte, iki kenar arasında ortak bir köşe varsa, iki kenarın bitişik olduğu söylenir. Burada, kenarların bitişikliği, iki kenarı birleştiren tek tepe noktası tarafından korunur.

Example 1

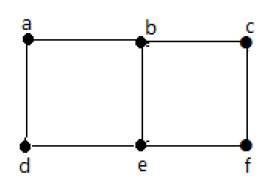
Yukarıdaki grafikte -

• Aralarında ortak bir kenar 'ab' olduğu için 'a' ve 'b' bitişik köşelerdir.

• Aralarında ortak bir kenar 'reklam' olduğundan 'a' ve 'd' bitişik köşelerdir.

• ab 've' be ', aralarında ortak bir köşe' b 'olduğu için bitişik kenarlardır.

• be 've' de ', aralarında ortak bir köşe' e 'olduğu için bitişik kenarlardır.

Example 2

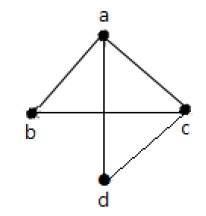
Yukarıdaki grafikte -

• Aralarında ortak bir kenar 'reklam' olduğundan 'a' ve 'd' bitişik köşelerdir.

• Aralarında ortak bir kenar 'cb' olduğu için 'c' ve 'b' bitişik köşelerdir.

• 'ad' ve 'cd', aralarında ortak bir köşe 'd' olduğu için bitişik kenarlardır.

• 'ac' ve 'cd', aralarında ortak bir köşe 'c' olduğu için bitişik kenarlardır.

Paralel Kenarlar

Bir grafikte, bir çift köşe birden fazla kenarla bağlanırsa, bu kenarlara paralel kenarlar denir.

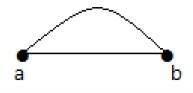
Yukarıdaki grafikte, 'a' ve 'b', aralarında 'ab' ve 'ab' olmak üzere iki kenarla birbirine bağlanan iki köşedir. Bu nedenle paralel kenar olarak adlandırılır.

Çoklu Grafik

Paralel kenarlara sahip bir grafik, Multigraph olarak bilinir.

Example 1

Yukarıdaki grafikte 'ab', 'ac', 'cd', 'cd' ve 'bd' olmak üzere beş kenar vardır. 'C' ve 'd' aralarında iki paralel kenar olduğundan, bu bir Multigraph.

Example 2

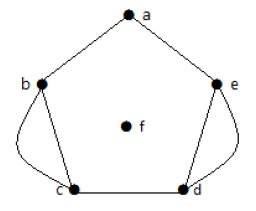
Yukarıdaki grafikte, 'b' ve 'c' köşelerinin iki kenarı vardır. 'E' ve 'd' köşelerinin de aralarında iki kenar vardır. Dolayısıyla bir Multigraph.

Bir Grafiğin Derece Sırası

Bir grafikteki tüm köşelerin dereceleri azalan veya artan sırada düzenlenmişse, elde edilen sıra grafiğin derece dizisi olarak bilinir.

Example 1

Köşe	Bir	b	c	d	e
Bağlanıyor	M.Ö	a, d	a, d	c, b, e	d
Derece	2	2	2	3	1

Yukarıdaki grafikte, {d, a, b, c, e} köşeleri için derece dizisi {3, 2, 2, 2, 1} 'dir.

Example 2

Köşe	Bir	b	c	d	e	f
Bağlanıyor	b, e	AC	b, d	c, e	a, d	-
Derece	2	2	2	2	2	0

Yukarıdaki grafikte, {a, b, c, d, e, f} köşeleri için derece dizisi {2, 2, 2, 2, 2, 0} 'dir.

Grafikler, yapılarına bağlı olarak grafiklerin karakterizasyonu için kullanılan çeşitli özelliklere sahiptir. Bu özellikler, grafik teorisinin alanına ilişkin belirli terimlerle tanımlanmıştır. Bu bölümde, tüm grafiklerde ortak olan birkaç temel özelliği tartışacağız.

İki Tepe Arası Mesafe

Köşe U ve Köşe V arasındaki en kısa yoldaki kenarların sayısıdır. İki köşeyi birbirine bağlayan birden çok yol varsa, en kısa yol, iki köşe arasındaki mesafe olarak kabul edilir.

Gösterim - d (U, V)

Bir tepe noktasından diğerine herhangi bir sayıda yol olabilir. Bunlar arasında sadece en kısa olanı seçmeniz gerekiyor.

Example

Aşağıdaki grafiğe bir göz atın -

Burada, tepe 'd' ile tepe 'e' arasındaki mesafe veya sadece 'de', aralarında bir kenar olduğu için 1'dir. 'D' tepe noktasından 'e' tepe noktasına kadar birçok yol vardır -

• da, ab, be
• df, fg, ge
• de (Köşeler arasındaki mesafe dikkate alınır)
• df, fc, ca, ab, be
• da, ac, cf, fg, ge

Bir Vertex'in Eksantrikliği

Bir tepe ile diğer tüm tepe noktaları arasındaki maksimum mesafe, tepe noktasının eksantrikliği olarak kabul edilir.

Gösterim - e (V)

Grafikteki belirli bir tepe noktasından diğer tüm köşelere olan mesafe alınır ve bu mesafeler arasında eksantriklik, mesafelerin en yüksek olanıdır.

Example

Yukarıdaki grafikte "a" nın eksantrikliği 3'tür.

'A' ile 'b' arasındaki mesafe 1'dir ('ab'),

'a' dan 'c' ye 1 ('ac'),

"a" dan "d" ye 1 ("reklam"),

'a'dan' e'ye kadar 2 ('ab' - 'be') veya ('ad' - 'de'),

'a'dan' f'ye kadar 2 ('ac' - 'cf') veya ('reklam' - 'df'),

'a'dan' g'ye kadar 3 ('ac' - 'cf' - 'fg') veya ('ad' - 'df' - 'fg').

Dolayısıyla, eksantriklik 3'tür, bu maksimum olan 'ag' arasındaki mesafeden 'a' tepe noktasından maksimumdur.

Başka bir deyişle,

e (b) = 3

e (c) = 3

e (d) = 2

e (e) = 3

e (f) = 3

e (g) = 3

Bağlı Grafiğin Yarıçapı

Tüm köşelerden gelen minimum dış merkezlilik, Grafik G'nin yarıçapı olarak kabul edilir. Bir tepe ile diğer tüm köşeler arasındaki tüm maksimum mesafeler arasındaki minimum, Grafik G'nin yarıçapı olarak kabul edilir.

Gösterim - r (G)

Bir grafikteki köşelerin tüm eksantrikliklerinden, bağlantılı grafiğin yarıçapı, tüm bu eksantrikliklerin minimumudur.

Example

Yukarıdaki grafikte r (G) = 2, 'd' için minimum dışmerkezlik.

Bir Grafiğin Çapı

Tüm köşelerden gelen maksimum dış merkezlilik, Grafik G'nin çapı olarak kabul edilir. Bir tepe ile diğer tüm köşeler arasındaki tüm mesafeler arasındaki maksimum, Grafik G'nin çapı olarak kabul edilir.

Notation − d(G) - Bir grafikteki köşelerin tüm eksantrikliklerinden, bağlı grafiğin çapı tüm bu eksantrikliklerin maksimumudur.

Example

Yukarıdaki grafikte, d (G) = 3; bu maksimum eksantrikliktir.

Merkez nokta

Bir grafiğin eksantrikliği yarıçapına eşitse, grafiğin merkez noktası olarak bilinir. Eğer

e (V) = r (V),

daha sonra 'V', 'G' grafiğinin merkezi noktasıdır.

Example

Örnek grafikte, 'd' grafiğin merkez noktasıdır.

e (d) = r (d) = 2

Merkez

'G'nin tüm merkezi noktalarının kümesi, Grafiğin merkezi olarak adlandırılır.

Example

Örnek grafikte, {'d'} Grafiğin merkezidir.

Çevre

number of edges in the longest cycle of ‘G’ "G" nin çevresi olarak adlandırılır.

Example

Örnek grafikte çevre, en uzun döngü olan acfgeba veya acfdeba'dan elde ettiğimiz 6'dır.

Çevresi

En kısa 'G' döngüsündeki kenar sayısına Girth denir.

Notation: İyi oyun).

Example - Örnek grafikte, grafiğin çevresi 4'tür ve bu en kısa döngü acfda veya dfged veya abeda'dan türetilmiştir.

Tepe Noktalarının Derecelerinin Toplamı Teoremi

G = (V, E) V = {V ₁ , V ₂ ,… V _n } köşeleri olan yönlendirilmemiş bir grafikse, o zaman

n Σ ben = 1 derece (V _ben ) = 2 | E |

Corollary 1

Eğer G = (V, E) V = {V ₁ , V ₂ ,… V _n } köşeleri olan yönlendirilmiş bir grafikse , o zaman

n Σ ben = 1 derece + (V _ben ) = | E | = n Σ ben = 1 derece (V _ben )

Corollary 2

Yönlendirilmemiş herhangi bir grafikte, Tek dereceli köşe sayısı Çifttir.

Corollary 3

Yönlendirilmemiş bir grafikte, her bir tepe noktasının derecesi k ise, o zaman

k | V | = 2 | E |

Corollary 4

Yönlendirilmemiş bir grafikte, her bir tepe noktasının derecesi en az k ise, o zaman

k | V | ≤ 2 | E |

| Corollary 5

Yönlendirilmemiş bir grafikte, her bir tepe noktasının derecesi en fazla k ise, o zaman

k | V | ≥ 2 | E |

Köşe sayısına, kenar sayısına, ara bağlantıya ve genel yapılarına bağlı olarak çeşitli grafik türleri vardır. Bu bölümde sadece birkaç önemli grafik türünü tartışacağız.

Boş Grafik

A graph having no edges Boş Grafik olarak adlandırılır.

Misal

Yukarıdaki grafikte 'a', 'b' ve 'c' adlı üç köşe vardır, ancak aralarında kenar yoktur. Dolayısıyla bir Boş Grafiktir.

Önemsiz Grafik

Bir graph with only one vertex Önemsiz Grafik olarak adlandırılır.

Misal

Yukarıda gösterilen grafikte, başka hiçbir kenarı olmayan yalnızca bir köşe 'a' vardır. Dolayısıyla, Önemsiz bir grafiktir.

Yönlendirilmemiş Grafik

Yönlü olmayan bir grafik kenarları içerir, ancak kenarlar yönlendirilmiş değildir.

Misal

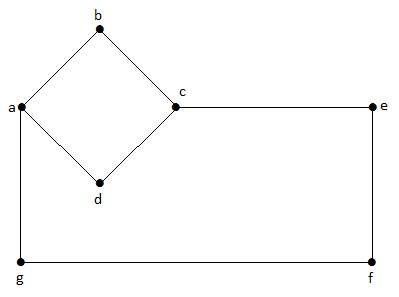
Bu grafikte, 'a', 'b', 'c', 'd', 'e', ​​'f', 'g' köşelerdir ve 'ab', 'bc', 'cd', 'da ',' ag ',' gf ',' ef 'grafiğin kenarlarıdır. Yönlü olmayan bir grafik olduğundan, 'ab' ve 'ba' kenarları aynıdır. Benzer şekilde diğer kenarlar da aynı şekilde değerlendirilir.

Yönlendirilmiş grafik

Yönlendirilmiş bir grafikte, her kenarın bir yönü vardır.

Misal

Yukarıdaki grafikte yedi köşemiz var 'a', 'b', 'c', 'd', 'e', ​​'f' ve 'g' ve sekiz kenar 'ab', 'cb', ' dc ',' ad ',' ec ',' fe ',' gf 've' ga '. Yönlendirilmiş bir grafik olduğundan, her bir kenar, yönünü gösteren bir ok işareti taşır. Yönlendirilmiş bir grafikte "ab" nin "ba" dan farklı olduğuna dikkat edin.

Basit Grafik

Grafik with no loops ve hayır parallel edges basit grafik olarak adlandırılır.

• 'N' köşeli tek bir grafikte mümkün olan maksimum kenar sayısı ⁿ C _2'dir, burada ⁿ C ₂ = n (n - 1) / 2.

• 'N' köşeli olası basit grafik sayısı = 2 _{ⁿ c 2} = 2 ^{n (n-1) / 2} .

Misal

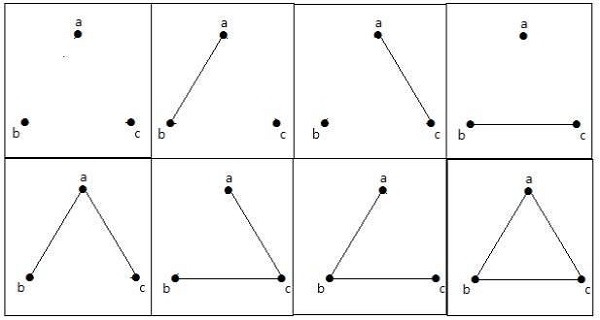
Aşağıdaki grafikte, paralel kenarlar ve ilmekler hariç maksimum 3 kenarlı 3 köşe bulunmaktadır. Bu, yukarıdaki formüller kullanılarak kanıtlanabilir.

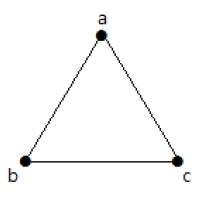
N = 3 köşeli maksimum kenar sayısı -

ⁿ C ₂ = n (n – 1) / 2

= 3 (3–1) / 2

= 6/2

= 3 kenar

N = 3 köşeli maksimum basit grafik sayısı -

2 _{ⁿ C 2} = 2 ^{n (n-1) / 2}

= 2 ^{3 (3-1) / 2}

= 2 ³

8

Bu 8 grafik aşağıda gösterildiği gibidir -

Bağlı Grafik

Bir G grafiğinin bağlı olduğu söyleniyor if there exists a path between every pair of vertices. Grafikteki her köşe için en az bir kenar olmalıdır. Böylece kenarın diğer tarafında başka bir tepe noktasına bağlı olduğunu söyleyebiliriz.

Misal

Aşağıdaki grafikte, her tepe noktasının diğer kenara bağlı kendi kenarı vardır. Dolayısıyla bağlantılı bir grafiktir.

Bağlantısız Grafik

En az iki bağlantılı köşe içermeyen bir G grafiğinin bağlantısı kesilir.

örnek 1

Aşağıdaki grafik, biri 'a', 'b', 'c', 'd' köşeli ve diğeri 'e', ​​'f', 'g' olmak üzere iki bileşenin olduğu bir Bağlantısız Grafik örneğidir. 'h' köşeleri.

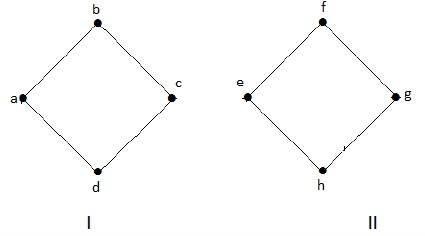
İki bileşen bağımsızdır ve birbirine bağlı değildir. Bu nedenle bağlantısız grafik denir.

Örnek 2

Bu örnekte, birbirine bağlı olmayan iki bağımsız bileşen vardır: abfe ve cd. Dolayısıyla bu, bağlantısız bir grafiktir.

Normal Grafik

Bir G grafiğinin düzgün olduğu söylenir, if all its vertices have the same degree. Bir grafikte, her bir tepe noktasının derecesi 'k' ise, o zaman grafiğe 'k-normal grafik' denir.

Misal

Aşağıdaki grafiklerde, tüm köşeler aynı dereceye sahiptir. Bu grafiklere normal grafikler denir.

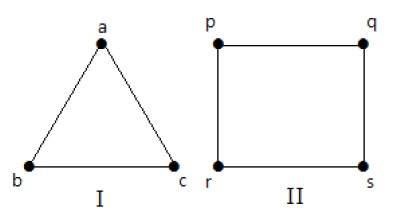
Her iki grafikte de, tüm köşeler 2. dereceye sahiptir. Bunlara 2-Normal Grafikler denir.

Tam Grafik

'N' karşılıklı köşeli basit bir grafiğe tam grafik denir ve denoted by ‘K_n’. Grafikte,a vertex should have edges with all other vertices, sonra tam bir grafik olarak adlandırıldı.

Başka bir deyişle, bir tepe noktası bir grafikteki diğer tüm köşelere bağlanırsa, o zaman buna tam grafik denir.

Misal

Aşağıdaki grafiklerde, grafikteki her köşe, kendisi hariç, grafikte kalan tüm köşelere bağlıdır.

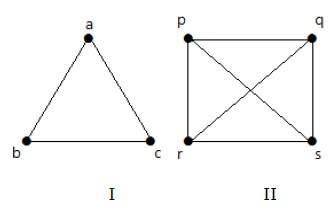
Grafik I'de,

	a	b	c
a	Bağlı değil	Bağlandı	Bağlandı
b	Bağlandı	Bağlı değil	Bağlandı
c	Bağlandı	Bağlandı	Bağlı değil

Grafik II'de,

	p	q	r	s
p	Bağlı değil	Bağlandı	Bağlandı	Bağlandı
q	Bağlandı	Bağlı değil	Bağlandı	Bağlandı
r	Bağlandı	Bağlandı	Bağlı değil	Bağlandı
s	Bağlandı	Bağlandı	Bağlandı	Bağlı değil

Döngü Grafiği

'N' köşeli (n> = 3) ve 'n' kenarlı basit bir grafiğe, tüm kenarları 'n' uzunluğunda bir döngü oluşturuyorsa, döngü grafiği denir.

Grafikteki her bir tepe noktasının derecesi iki ise, buna Döngü Grafiği denir.

Notation- C _n

Misal

Aşağıdaki grafiklere bir göz atın -

• Grafik I, bir 'ab-bc-ca' döngüsü oluşturan 3 kenarlı 3 köşeye sahiptir.

• Grafik II, bir 'pq-qs-sr-rp' döngüsü oluşturan 4 kenarlı 4 köşeye sahiptir.

• Grafik III 'ik-km-ml-lj-ji' döngüsünü oluşturan 5 kenarlı 5 köşeye sahiptir.

Dolayısıyla verilen tüm grafikler döngü grafikleridir.

Tekerlek Grafiği

Yeni bir tepe noktası eklenerek C _n-1 döngü grafiğinden bir tekerlek grafiği elde edilir . Bu yeni tepe noktasına aHubC _n'nin tüm köşelerine bağlı olan .

Gösterim - W _n

W _cinsinden kenar sayısı _n = Göbekten diğer tüm köşelere kadar olan kenar sayısı +

Hub olmadan döngü grafiğindeki diğer tüm düğümlerin kenar sayısı.

= (n – 1) + (n – 1)

= 2 (n – 1)

Misal

Aşağıdaki grafiklere bir göz atın. Hepsi çark grafikleri.

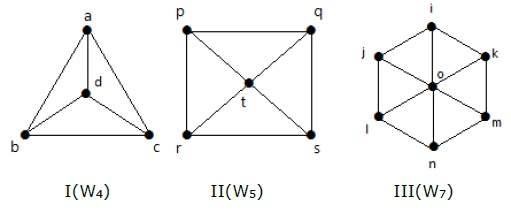
Grafik I'de, ortada 'd' olarak adlandırılan bir köşe eklenerek C _3'ten elde edilir . W ₄ olarak belirtilmiştir .

W4 = 2 (n-1) = 2 (3) = 6'daki kenar sayısı

Grafik II'de, C4'ten ortada 't' olarak adlandırılan bir köşe eklenerek elde edilir. W ₅ olarak belirtilir .

W5 = 2 (n-1) = 2 (4) = 8'deki kenar sayısı

Grafik III'te, ortada 'o' olarak adlandırılan bir köşe eklenerek C _6'dan elde edilir . W ₇ olarak belirtilir .

W4 = 2 (n-1) = 2 (6) = 12'deki kenar sayısı

Döngüsel Grafik

Grafik with at least one döngü döngüsel grafik olarak adlandırılır.

Misal

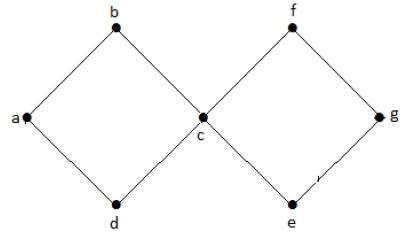
Yukarıdaki örnek grafikte, abcda ve cfgec olmak üzere iki döngü var. Bu nedenle döngüsel grafik olarak adlandırılır.

Asiklik Grafik

A graph with no cycles is called an acyclic graph.

Example

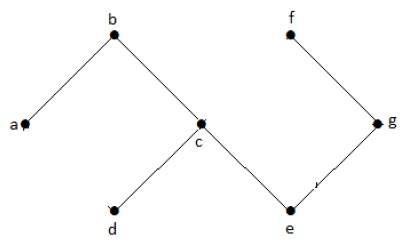
In the above example graph, we do not have any cycles. Hence it is a non-cyclic graph.

Bipartite Graph

A simple graph G = (V, E) with vertex partition V = {V₁, V₂} is called a bipartite graph if every edge of E joins a vertex in V1 to a vertex in V₂.

In general, a Bipertite graph has two sets of vertices, let us say, V1 and V2, and if an edge is drawn, it should connect any vertex in set V₁ to any vertex in set V₂.

Example

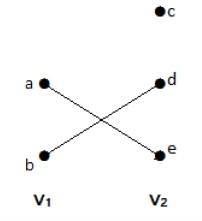
In this graph, you can observe two sets of vertices − V₁ and V₂. Here, two edges named ‘ae’ and ‘bd’ are connecting the vertices of two sets V₁ and V₂.

Complete Bipartite Graph

A bipartite graph ‘G’, G = (V, E) with partition V = {V₁, V₂} is said to be a complete bipartite graph if every vertex in V₁ is connected to every vertex of V₂.

In general, a complete bipartite graph connects each vertex from set V₁ to each vertex from set V₂.

Example

The following graph is a complete bipartite graph because it has edges connecting each vertex from set V₁ to each vertex from set V₂.

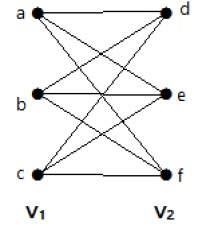
If |V₁| = m and |V₂| = n, then the complete bipartite graph is denoted by K_{m, n}.

• K_m,n has (m+n) vertices and (mn) edges.
• K_m,n is a regular graph if m=n.

In general, a complete bipartite graph is not a complete graph.

K_m,n is a complete graph if m=n=1.

The maximum number of edges in a bipartite graph with n vertices is −

[n²/4]

If n=10, k5, 5= [n2/4] = [10²/4] = 25.

Similarly, K6, 4=24

K7, 3=21

K8, 2=16

K9, 1=9

If n=9, k5, 4 = [n2/4] = [92/4] = 20

Similarly, K6, 3=18

K7, 2=14

K8, 1=8

‘G’ is a bipartite graph if ‘G’ has no cycles of odd length. A special case of bipartite graph is a star graph.

Star Graph

A complete bipartite graph of the form K1, n-1 is a star graph with n-vertices. A star graph is a complete bipartite graph if a single vertex belongs to one set and all the remaining vertices belong to the other set.

Example

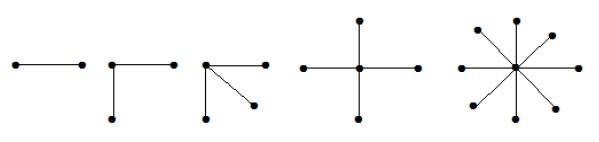
In the above graphs, out of ‘n’ vertices, all the ‘n–1’ vertices are connected to a single vertex. Hence it is in the form of K¹, ^n-1 which are star graphs.

Complement of a Graph

Let 'G−' be a simple graph with some vertices as that of ‘G’ and an edge {U, V} is present in 'G−', if the edge is not present in G. It means, two vertices are adjacent in 'G−' if the two vertices are not adjacent in G.

If the edges that exist in graph I are absent in another graph II, and if both graph I and graph II are combined together to form a complete graph, then graph I and graph II are called complements of each other.

Example

In the following example, graph-I has two edges ‘cd’ and ‘bd’. Its complement graph-II has four edges.

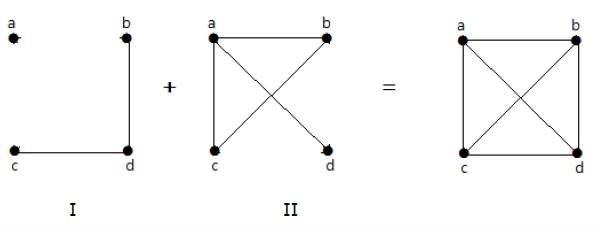
Note that the edges in graph-I are not present in graph-II and vice versa. Hence, the combination of both the graphs gives a complete graph of ‘n’ vertices.

Note − A combination of two complementary graphs gives a complete graph.

If ‘G’ is any simple graph, then

|E(G)| + |E('G-')| = |E(Kn)|, where n = number of vertices in the graph.

Example

Let ‘G’ be a simple graph with nine vertices and twelve edges, find the number of edges in 'G-'.

You have, |E(G)| + |E('G-')| = |E(Kn)|

12 + |E('G-')| =

9(9-1) / 2 = ⁹C₂

12 + |E('G-')| = 36

|E('G-')| = 24

‘G’ is a simple graph with 40 edges and its complement 'G−' has 38 edges. Find the number of vertices in the graph G or 'G−'.

Let the number of vertices in the graph be ‘n’.

We have, |E(G)| + |E('G-')| = |E(Kn)|

40 + 38 = n(n-1)/2

156 = n(n-1)

13(12) = n(n-1)

n = 13

Trees are graphs that do not contain even a single cycle. They represent hierarchical structure in a graphical form. Trees belong to the simplest class of graphs. Despite their simplicity, they have a rich structure.

Trees provide a range of useful applications as simple as a family tree to as complex as trees in data structures of computer science.

Tree

A connected acyclic graph is called a tree. In other words, a connected graph with no cycles is called a tree.

The edges of a tree are known as branches. Elements of trees are called their nodes. The nodes without child nodes are called leaf nodes.

A tree with ‘n’ vertices has ‘n-1’ edges. If it has one more edge extra than ‘n-1’, then the extra edge should obviously has to pair up with two vertices which leads to form a cycle. Then, it becomes a cyclic graph which is a violation for the tree graph.

Example 1

The graph shown here is a tree because it has no cycles and it is connected. It has four vertices and three edges, i.e., for ‘n’ vertices ‘n-1’ edges as mentioned in the definition.

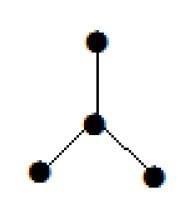
Note − Every tree has at least two vertices of degree one.

Example 2

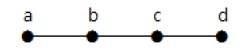
In the above example, the vertices ‘a’ and ‘d’ has degree one. And the other two vertices ‘b’ and ‘c’ has degree two. This is possible because for not forming a cycle, there should be at least two single edges anywhere in the graph. It is nothing but two edges with a degree of one.

Forest

A disconnected acyclic graph is called a forest. In other words, a disjoint collection of trees is called a forest.

Example

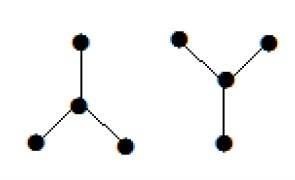
The following graph looks like two sub-graphs; but it is a single disconnected graph. There are no cycles in this graph. Hence, clearly it is a forest.

Spanning Trees

Let G be a connected graph, then the sub-graph H of G is called a spanning tree of G if −

• H is a tree
• H contains all vertices of G.

A spanning tree T of an undirected graph G is a subgraph that includes all of the vertices of G.

Example

In the above example, G is a connected graph and H is a sub-graph of G.

Clearly, the graph H has no cycles, it is a tree with six edges which is one less than the total number of vertices. Hence H is the Spanning tree of G.

Circuit Rank

Let ‘G’ be a connected graph with ‘n’ vertices and ‘m’ edges. A spanning tree ‘T’ of G contains (n-1) edges.

Therefore, the number of edges you need to delete from ‘G’ in order to get a spanning tree = m-(n-1), which is called the circuit rank of G.

This formula is true, because in a spanning tree you need to have ‘n-1’ edges. Out of ‘m’ edges, you need to keep ‘n–1’ edges in the graph.

Hence, deleting ‘n–1’ edges from ‘m’ gives the edges to be removed from the graph in order to get a spanning tree, which should not form a cycle.

Example

Take a look at the following graph −

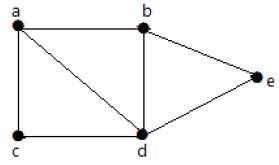
For the graph given in the above example, you have m=7 edges and n=5 vertices.

Then the circuit rank is −

G = m – (n – 1)

= 7 – (5 – 1)

= 3

Example

Let ‘G’ be a connected graph with six vertices and the degree of each vertex is three. Find the circuit rank of ‘G’.

By the sum of degree of vertices theorem,

n Σ i=1 deg(V _i) = 2|E|

6 × 3 = 2|E|

|E| = 9

Circuit rank = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

Kirchoff’s Theorem

Kirchoff’s theorem is useful in finding the number of spanning trees that can be formed from a connected graph.

Example

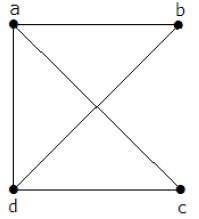
The matrix ‘A’ be filled as, if there is an edge between two vertices, then it should be given as ‘1’, else ‘0’.

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

By using kirchoff's theorem, it should be changed as replacing the principle diagonal values with the degree of vertices and all other elements with -1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

Thus, the number of spanning trees = 8.

Whether it is possible to traverse a graph from one vertex to another is determined by how a graph is connected. Connectivity is a basic concept in Graph Theory. Connectivity defines whether a graph is connected or disconnected. It has subtopics based on edge and vertex, known as edge connectivity and vertex connectivity. Let us discuss them in detail.

Connectivity

A graph is said to be connected if there is a path between every pair of vertex. From every vertex to any other vertex, there should be some path to traverse. That is called the connectivity of a graph. A graph with multiple disconnected vertices and edges is said to be disconnected.

Example 1

In the following graph, it is possible to travel from one vertex to any other vertex. For example, one can traverse from vertex ‘a’ to vertex ‘e’ using the path ‘a-b-e’.

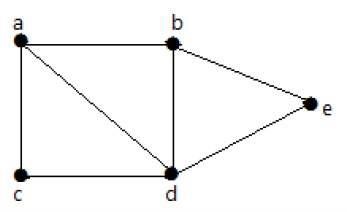
Example 2

In the following example, traversing from vertex ‘a’ to vertex ‘f’ is not possible because there is no path between them directly or indirectly. Hence it is a disconnected graph.

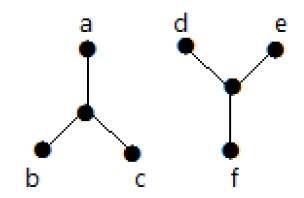
Cut Vertex

Let ‘G’ be a connected graph. A vertex V ∈ G is called a cut vertex of ‘G’, if ‘G-V’ (Delete ‘V’ from ‘G’) results in a disconnected graph. Removing a cut vertex from a graph breaks it in to two or more graphs.

Note − Removing a cut vertex may render a graph disconnected.

A connected graph ‘G’ may have at most (n–2) cut vertices.

Example

In the following graph, vertices ‘e’ and ‘c’ are the cut vertices.

By removing ‘e’ or ‘c’, the graph will become a disconnected graph.

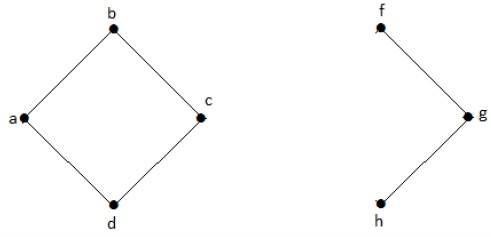
Without ‘g’, there is no path between vertex ‘c’ and vertex ‘h’ and many other. Hence it is a disconnected graph with cut vertex as ‘e’. Similarly, ‘c’ is also a cut vertex for the above graph.

Cut Edge (Bridge)

Let ‘G’ be a connected graph. An edge ‘e’ ∈ G is called a cut edge if ‘G-e’ results in a disconnected graph.

If removing an edge in a graph results in to two or more graphs, then that edge is called a Cut Edge.

Example

In the following graph, the cut edge is [(c, e)].

By removing the edge (c, e) from the graph, it becomes a disconnected graph.

In the above graph, removing the edge (c, e) breaks the graph into two which is nothing but a disconnected graph. Hence, the edge (c, e) is a cut edge of the graph.

Note − Let ‘G’ be a connected graph with ‘n’ vertices, then

• a cut edge e ∈ G if and only if the edge ‘e’ is not a part of any cycle in G.

• the maximum number of cut edges possible is ‘n-1’.

• whenever cut edges exist, cut vertices also exist because at least one vertex of a cut edge is a cut vertex.

• if a cut vertex exists, then a cut edge may or may not exist.

Cut Set of a Graph

Let ‘G’= (V, E) be a connected graph. A subset E’ of E is called a cut set of G if deletion of all the edges of E’ from G makes G disconnect.

If deleting a certain number of edges from a graph makes it disconnected, then those deleted edges are called the cut set of the graph.

Example

Take a look at the following graph. Its cut set is E1 = {e1, e3, e5, e8}.

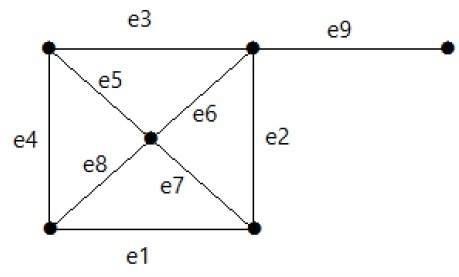
After removing the cut set E1 from the graph, it would appear as follows −

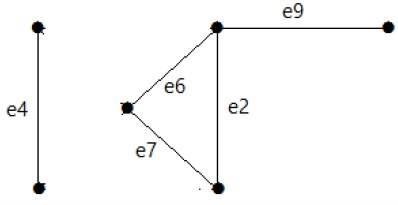
Similarly, there are other cut sets that can disconnect the graph −

• E3 = {e9} – Smallest cut set of the graph.

• E4 = {e3, e4, e5}

Edge Connectivity

Let ‘G’ be a connected graph. The minimum number of edges whose removal makes ‘G’ disconnected is called edge connectivity of G.

Notation − λ(G)

In other words, the number of edges in a smallest cut set of G is called the edge connectivity of G.

If ‘G’ has a cut edge, then λ(G) is 1. (edge connectivity of G.)

Example

Take a look at the following graph. By removing two minimum edges, the connected graph becomes disconnected. Hence, its edge connectivity (λ(G)) is 2.

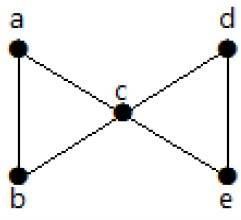
Here are the four ways to disconnect the graph by removing two edges −

Vertex Connectivity

Let ‘G’ be a connected graph. The minimum number of vertices whose removal makes ‘G’ either disconnected or reduces ‘G’ in to a trivial graph is called its vertex connectivity.

Notation − K(G)

Example

In the above graph, removing the vertices ‘e’ and ‘i’ makes the graph disconnected.

If G has a cut vertex, then K(G) = 1.

Notation − For any connected graph G,

K(G) ≤ λ(G) ≤ δ(G)

Vertex connectivity (K(G)), edge connectivity (λ(G)), minimum number of degrees of G(δ(G)).

Example

Calculate λ(G) and K(G) for the following graph −

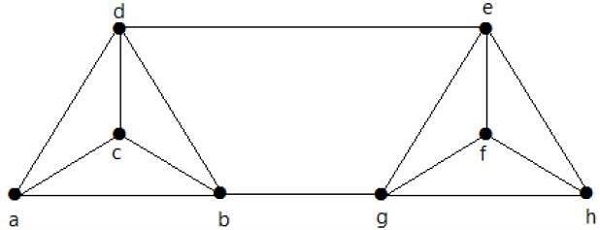
Solution

From the graph,

δ(G) = 3

K(G) ≤ λ(G) ≤ δ(G) = 3 (1)

K(G) ≥ 2 (2)

Deleting the edges {d, e} and {b, h}, we can disconnect G.

Therefore,

λ(G) = 2

2 ≤ λ(G) ≤ δ(G) = 2 (3)

From (2) and (3), vertex connectivity K(G) = 2

A covering graph is a subgraph which contains either all the vertices or all the edges corresponding to some other graph. A subgraph which contains all the vertices is called a line/edge covering. A subgraph which contains all the edges is called a vertex covering.

Line Covering

Let G = (V, E) be a graph. A subset C(E) is called a line covering of G if every vertex of G is incident with at least one edge in C, i.e.,

deg(V) ≥ 1 ∀ V ∈ G

because each vertex is connected with another vertex by an edge. Hence it has a minimum degree of 1.

Example

Take a look at the following graph −

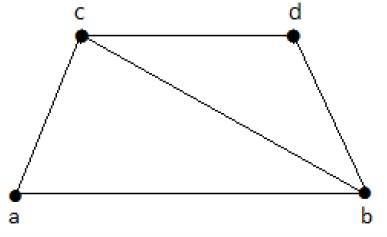
Its subgraphs having line covering are as follows −

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

Line covering of ‘G’ does not exist if and only if ‘G’ has an isolated vertex. Line covering of a graph with ‘n’ vertices has at least [n/2] edges.

Minimal Line Covering

A line covering C of a graph G is said to be minimal if no edge can be deleted from C.

Example

In the above graph, the subgraphs having line covering are as follows −

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

Here, C₁, C₂, C₃ are minimal line coverings, while C₄ is not because we can delete {b, c}.

Minimum Line Covering

It is also known as Smallest Minimal Line Covering. A minimal line covering with minimum number of edges is called a minimum line covering of ‘G’. The number of edges in a minimum line covering in ‘G’ is called the line covering number of ‘G’ (α₁).

Example

In the above example, C₁ and C₂ are the minimum line covering of G and α₁ = 2.

• Every line covering contains a minimal line covering.

• Every line covering does not contain a minimum line covering (C₃ does not contain any minimum line covering.

• No minimal line covering contains a cycle.

• If a line covering ‘C’ contains no paths of length 3 or more, then ‘C’ is a minimal line covering because all the components of ‘C’ are star graph and from a star graph, no edge can be deleted.

Vertex Covering

Let ‘G’ = (V, E) be a graph. A subset K of V is called a vertex covering of ‘G’, if every edge of ‘G’ is incident with or covered by a vertex in ‘K’.

Example

Take a look at the following graph −

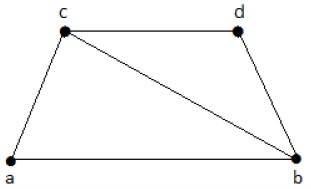
The subgraphs that can be derived from the above graph are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

K₄ = {a, d}

Here, K₁, K₂, and K₃ have vertex covering, whereas K₄ does not have any vertex covering as it does not cover the edge {bc}.

Minimal Vertex Covering

A vertex ‘K’ of graph ‘G’ is said to be minimal vertex covering if no vertex can be deleted from ‘K’.

Example

In the above graph, the subgraphs having vertex covering are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

Here, K₁ and K₂ are minimal vertex coverings, whereas in K₃, vertex ‘d’ can be deleted.

Minimum Vertex Covering

It is also known as the smallest minimal vertex covering. A minimal vertex covering of graph ‘G’ with minimum number of vertices is called the minimum vertex covering.

The number of vertices in a minimum vertex covering of ‘G’ is called the vertex covering number of G (α₂).

Example

In the following graph, the subgraphs having vertex covering are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

Here, K₁ is a minimum vertex cover of G, as it has only two vertices. α₂ = 2.

A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex between any two edges.

Matching

Let ‘G’ = (V, E) be a graph. A subgraph is called a matching M(G), if each vertex of G is incident with at most one edge in M, i.e.,

deg(V) ≤ 1 ∀ V ∈ G

which means in the matching graph M(G), the vertices should have a degree of 1 or 0, where the edges should be incident from the graph G.

Notation − M(G)

Example

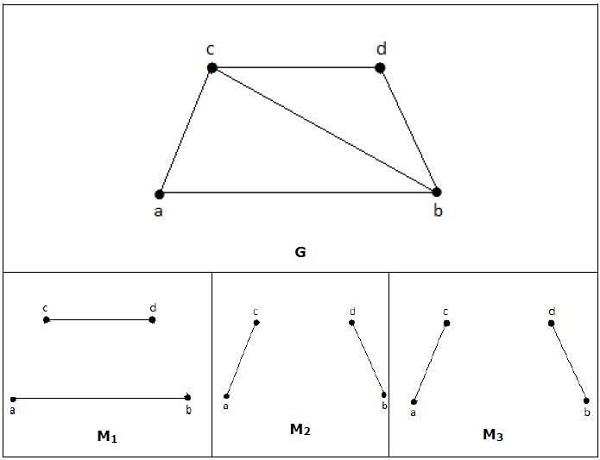
In a matching,

if deg(V) = 1, then (V) is said to be matched

if deg(V) = 0, then (V) is not matched.

In a matching, no two edges are adjacent. It is because if any two edges are adjacent, then the degree of the vertex which is joining those two edges will have a degree of 2 which violates the matching rule.

Maximal Matching

A matching M of graph ‘G’ is said to maximal if no other edges of ‘G’ can be added to M.

Example

M1, M2, M3 from the above graph are the maximal matching of G.

Maximum Matching

It is also known as largest maximal matching. Maximum matching is defined as the maximal matching with maximum number of edges.

The number of edges in the maximum matching of ‘G’ is called its matching number.

Example

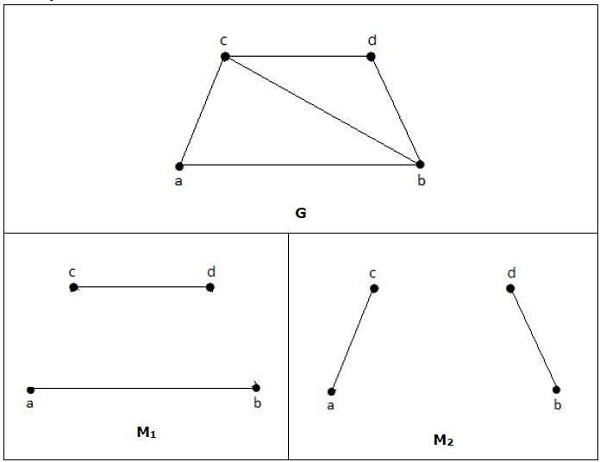
For a graph given in the above example, M1 and M2 are the maximum matching of ‘G’ and its matching number is 2. Hence by using the graph G, we can form only the subgraphs with only 2 edges maximum. Hence we have the matching number as two.

Perfect Matching

A matching (M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e.,

deg(V) = 1 ∀ V

The degree of each and every vertex in the subgraph should have a degree of 1.

Example

In the following graphs, M1 and M2 are examples of perfect matching of G.

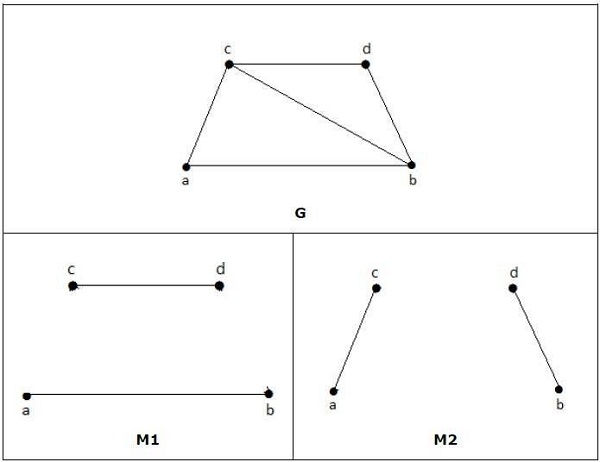
Note − Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.

A maximum matching of graph need not be perfect. If a graph ‘G’ has a perfect match, then the number of vertices |V(G)| is even. If it is odd, then the last vertex pairs with the other vertex, and finally there remains a single vertex which cannot be paired with any other vertex for which the degree is zero. It clearly violates the perfect matching principle.

Example

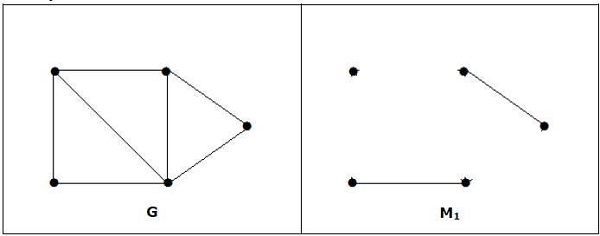
Note − The converse of the above statement need not be true. If G has even number of vertices, then M1 need not be perfect.

Example

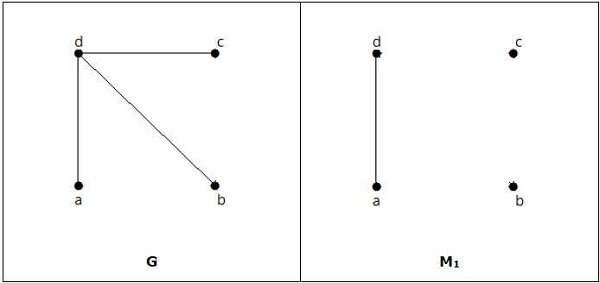
It is matching, but it is not a perfect match, even though it has even number of vertices.

Independent sets are represented in sets, in which

• there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.

• there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.

Independent Line Set

Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.

Example

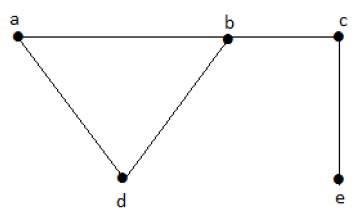
Let us consider the following subsets −

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.

Maximal Independent Line Set

An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.

Example

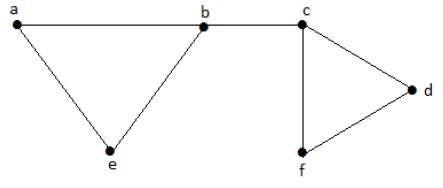
Let us consider the following subsets −

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₂ and L₃ are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.

Maximum Independent Line Set

A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

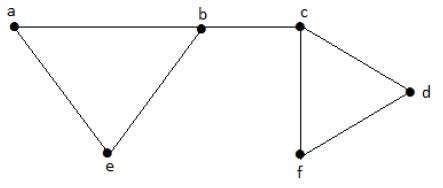
Let us consider the following subsets −

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₃ is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.

Note − For any graph G with no isolated vertex,

α1 + β1 = number of vertices in a graph = |V|

Example

Line covering number of K_n/C_n/w_n,

$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$

Line independent number (Matching number) = β₁ = [n/2] α₁ + β₁ = n.

Independent Vertex Set

Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.

Example

Consider the following subsets from the above graphs −

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Clearly S₁ is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S₂, S₃, and S₄ are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.

Maksimal Bağımsız Köşe Kümesi

'G' bir grafik olsun, o zaman bağımsız bir 'G' köşe kümesinin, 'S'ye başka bir' G 'tepe noktası eklenemiyorsa maksimum olduğu söylenir.

Example

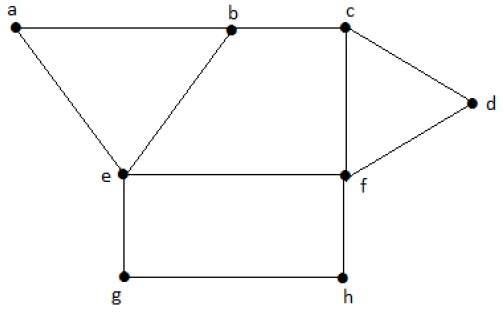
Yukarıdaki grafiklerden aşağıdaki alt kümeleri düşünün.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ ve S ₃ 'G' maksimal bağımsız tepe kümeleridir. S ₁ ve S _4'te başka köşeler ekleyebiliriz; fakat S ₂ ve S ₃ , herhangi bir başka köşe ekleyemezsiniz.

Maksimum Bağımsız Köşe Kümesi

Maksimum sayıda köşe noktasına sahip maksimum bağımsız köşe kümesi 'G', maksimum bağımsız köşe kümesi olarak adlandırılır.

Example

Yukarıdaki grafikten aşağıdaki alt kümeleri düşünün -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Yalnızca S ₃ , en yüksek sayıda köşeyi kapsadığından maksimum bağımsız köşe kümesidir. 'G'nin maksimum bağımsız köşe kümesindeki köşe noktası sayısına bağımsız köşe sayısı G (( ₂ ) denir .

Example

Tam grafik K _{n için} ,

Köşe kaplama sayısı = α ₂ = n − 1

Köşe bağımsız sayı = β ₂ = 1

Α ₂ + β ₂ = n'ye sahipsiniz

Tam bir grafikte, her köşe, kalan (n - 1) köşelerine bitişiktir. Bu nedenle, maksimum bağımsız bir K _n kümesi yalnızca bir köşe içerir.

Bu nedenle, β ₂ = 1

ve α ₂ = | v | - β ₂ = n-1

Note - Herhangi bir 'G' = (V, E) grafiği için

• α ₂ + β ₂ = | v |
• "S" bağımsız bir köşe kümesi "G" ise, (V - S) G'nin köşe kaplamasıdır.

Grafik renklendirme, bazı kısıtlamalar altında köşeler, kenarlar ve bölgeler gibi grafik bileşenlerini etiketlemenin basit bir yolundan başka bir şey değildir. Bir grafikte, iki bitişik köşe, bitişik kenarlar veya bitişik bölgeler minimum sayıda renkle renklendirilmez. Bu numarayachromatic number ve grafiğin adı a properly colored graph.

Grafik renklendirirken, grafik üzerinde ayarlanan kısıtlamalar renkler, renklendirme sırası, renk atama şekli vb. Bir tepe noktasına veya belirli bir bölgeye renklendirme verilir. Böylece, aynı renkteki tepe noktaları veya bölgeler bağımsız kümeler oluşturur.

Köşe Renklendirme

Köşe renklendirme, iki bitişik köşe aynı renge sahip olmayacak şekilde bir 'G' grafiğinin köşelerine renklerin atanmasıdır. Basitçe söylemek gerekirse, bir kenarın iki köşesi aynı renkte olmamalıdır.

Kromatik Sayı

'G' grafiğinin köşe renklendirmesi için gereken minimum renk sayısı, X (G) ile gösterilen G'nin kromatik sayısı olarak adlandırılır.

χ (G) = 1 ancak ve ancak 'G' bir boş grafikse. 'G' boş bir grafik değilse, χ (G) ≥ 2.

Example

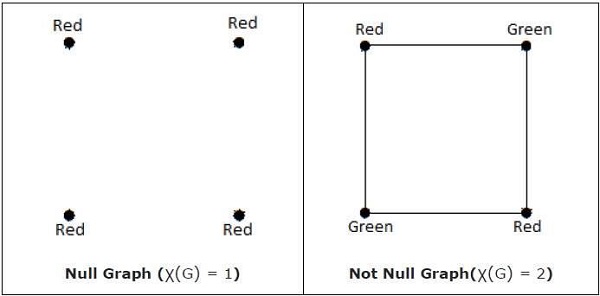
Note - En fazla n renk kullanan bir köşe renklendirmesi varsa, yani X (G) n ise, bir 'G' grafiğinin n-kaplanabilir olduğu söylenir.

Bölge Renklendirme

Bölge renklendirme, iki bitişik bölge aynı renge sahip olmayacak şekilde düzlemsel grafiğin bölgelerine renklerin atanmasıdır. Ortak bir kenara sahiplerse iki bölgenin bitişik olduğu söylenir.

Example

Aşağıdaki grafiğe bir göz atın. Bu iki bölge arasında ortak bir kenar 'be' olduğu için 'aeb' ve 'befc' bölgeleri bitişiktir.

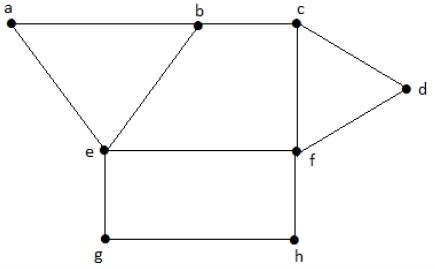
Benzer şekilde, diğer bölgeler de komşuluğa göre renklendirilir. Bu grafik aşağıdaki gibi renklendirilmiştir -

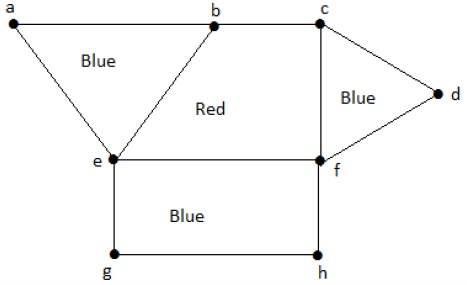
Example

Kn'in kromatik sayısı

• n
• n–1
• [n/2]
• [n/2]

Bu örneği K ₄ ile düşünün .

Tam grafikte, her köşe, kalan (n - 1) köşelere bitişiktir. Bu nedenle, her köşe için yeni bir renk gerekir. Dolayısıyla kromatik sayı K _n = n'dir.

Grafik Renklendirme Uygulamaları

Grafik renklendirme, grafik teorisindeki en önemli kavramlardan biridir. Bilgisayar biliminin birçok gerçek zamanlı uygulamasında kullanılır:

• Clustering
• Veri madenciliği
• Görüntü yakalama
• Resim parçalama
• Networking
• Kaynak tahsisi
• Süreç planlaması

Bir grafik aynı sayıda köşeye, kenara ve aynı zamanda aynı kenar bağlantısına sahip farklı formlarda mevcut olabilir. Bu tür grafiklere izomorfik grafikler denir. Bu bölümdeki grafikleri esas olarak bunlara atıfta bulunmak ve birbirlerinden tanımak amacıyla etiketlediğimize dikkat edin.

İzomorfik Grafikler

İki G ₁ ve G ₂ grafiğinin izomorf olduğu söylenir - eğer -

• Bileşen sayısı (köşeler ve kenarlar) aynıdır.

• Uç bağlantıları korunur.

Note- Kısacası, iki izomorfik grafikten biri diğerinin ince ayarlı versiyonu. Etiketsiz bir grafik, izomorfik bir grafik olarak da düşünülebilir.

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

G ₁ ≡ G _{2 ise} o zaman -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

G ₁ ve G _2'nin derece dizileri aynıdır.

{V ₁ , V ₂ , .. Vk} köşeleri G _1'de K uzunluğunda bir döngü oluşturuyorsa , {f (V ₁ ), f (V ₂ ),… f (Vk)} köşeleri bir döngü oluşturmalıdır G ₂ cinsinden K uzunluğunda .

Yukarıdaki koşulların tümü, G ₁ ve G ₂ grafiklerinin izomorfik olması için gereklidir, ancak grafiklerin izomorfik olduğunu kanıtlamak için yeterli değildir.

• (G ₁ ≡ G ₂ ) ancak ve ancak (G ₁ - ≡ G ₂ -) burada G ₁ ve G ₂ basit grafiklerdir.

• (G ₁ ≡ G ₂ ) G ₁ ve G _2'nin bitişik matrisleri aynıysa.

• (G ₁ ≡ G ₂ ) ancak ve ancak G ₁ ve G _2'nin karşılık gelen alt grafikleri (G1'deki bazı köşeler ve bunların grafik G _2'deki görüntüleri silinerek elde edilmiştir ) izomorfik ise.

Example

Aşağıdaki grafiklerden hangisi izomorfiktir?

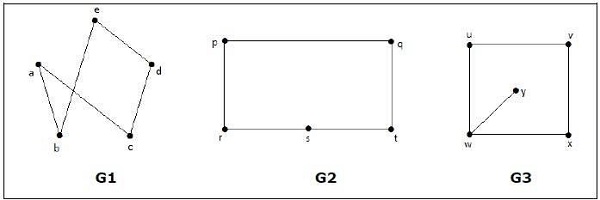
G ₃ grafiğinde , köşe 'w' yalnızca derece 3'e sahipken, diğer tüm grafik köşeleri 2. dereceye sahiptir. Dolayısıyla G3, G ₁ veya G _2'ye izomorfik değildir .

G ₁ ve G _2'yi tamamlayarak, sahip olduğunuz -

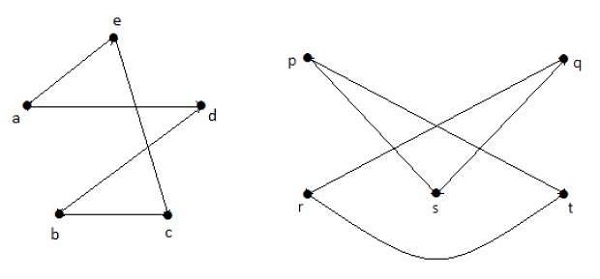
Burada, (G ₁ - ≡ G ₂ -), dolayısıyla (G ₁ ≡ G ₂ ).

Düzlemsel Grafikler

Bir 'G' grafiğinin, bir düzlem veya küre üzerinde çizilebiliyorsa, iki kenarın tepe noktası olmayan bir noktada birbiriyle kesişmemesi için düzlemsel olduğu söylenir.

Example

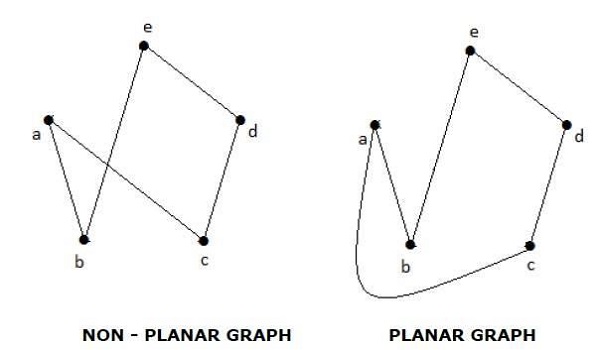
Bölgeler

Her düzlemsel grafik, düzlemi bölgeler adı verilen bağlantılı alanlara böler.

Example

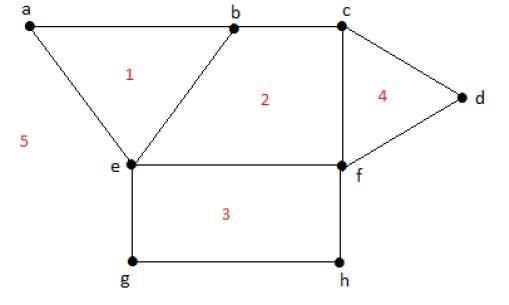
Sınırlı bir bölgenin derecesi r = deg(r) = Bölgeleri çevreleyen kenar sayısı r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8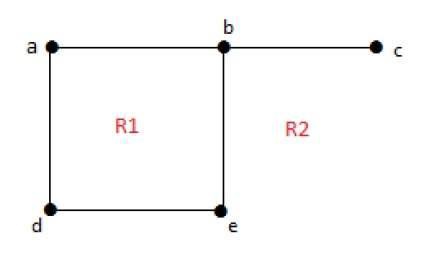

Sınırsız bir bölgenin derecesi r = deg(r) = Bölgeleri çevreleyen kenar sayısı r.

deg(R1) = 4
deg(R2) = 6

Düzlemsel grafiklerde aşağıdaki özellikler iyidir -

'N' köşeli düzlemsel bir grafikte, tüm köşelerin derecelerinin toplamı -

n Σ ben = 1 derece (V _ben ) = 2 | E |

Göre Sum of Degrees of Regions/ Teorem, 'n' bölgeli düzlemsel bir grafikte, bölgelerin derece toplamı -

n Σ ben = 1 derece (ri) = 2 | E |

Yukarıdaki teoreme dayanarak, aşağıdaki sonuçları çıkarabilirsiniz -

Düzlemsel bir grafikte,

Her bölgenin derecesi K ise, bölgelerin derecelerinin toplamı -

K | R | = 2 | E |

Her bölgenin derecesi en az K (≥ K) ise, o zaman

K | R | ≤ 2 | E |

Her bölgenin derecesi en fazla K (≤ K) ise, o zaman

K | R | ≥ 2 | E |

Note - Tüm bölgelerin aynı dereceye sahip olduğunu varsayalım.

Göre Euler’s Formulae düzlemsel grafiklerde,

Bir 'G' grafiği bağlantılı bir düzlemsel ise, o zaman

| V | + | R | = | E | + 2

'K' bileşenli bir düzlemsel grafik ise,

| V | + | R | = | E | + (K + 1)

Nerede, | V | köşe sayısıdır, | E | kenar sayısıdır ve | R | bölge sayısıdır.

Edge Vertex Eşitsizliği

'G', her bölgenin derecesi en az 'K' olan bağlantılı bir düzlemsel grafikse, o zaman,

| E | ≤ k / (k-2) {| v | - 2}

Biliyorsun, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

'G' basit bir bağlantılı düzlemsel grafikse,

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Deg (V) ≤ 5 olacak şekilde en az bir V • ∈ G tepe noktası vardır.

'G' basit bağlantılı bir düzlemsel grafikse (en az 2 kenarlı) ve üçgen yoksa, o zaman

|E| ≤ {2|V| – 4}

Kuratowski Teoremi

Bir grafik 'G', düzlemsel olmayan ise ve G '' K homeomorphic bir alt grafiğini sahip olması durumunda ₅ ya da K _3,3 .

Homomorfizm

G ₁ ve G ₂ grafiğinin homomorfik olduğu söylenir, eğer bu grafiklerin her biri G'nin bazı kenarlarını daha fazla köşeye bölerek aynı 'G' grafiğinden elde edilebilir. Aşağıdaki örneğe bir göz atın -

Bir köşe ekleyerek 'rs' kenarını iki kenara bölün.

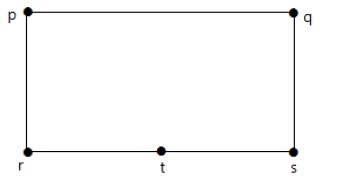
Aşağıda gösterilen grafikler ilk grafiğe homomorfiktir.

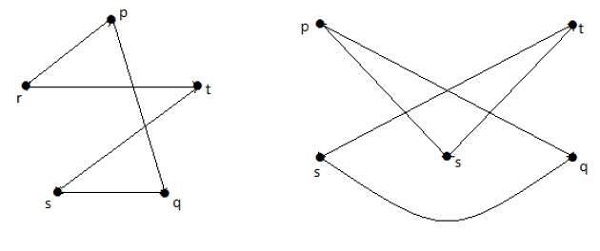
G ise ₁ G izomorf ₂ , daha sonra G G2 homeomorphic fakat tersi ihtiyaç doğru olmayabilir.

• 4 veya daha az köşeli herhangi bir grafik düzlemseldir.

• 8 veya daha az kenarlı herhangi bir grafik düzlemseldir.

• Tam bir K _n grafiği ancak ve ancak n ≤ 4 ise düzlemseldir.

• Tam iki taraflı grafik K _{m, n} , ancak ve ancak m ≤ 2 veya n ≤ 2 ise düzlemseldir.

• Minimum sayıda köşeye sahip basit bir düzlemsel olmayan grafik, K ₅ grafiğidir .

• Minimum kenar sayısına sahip basit düzlemsel olmayan grafik K _{3, 3'tür} .

Çok yüzlü grafik

Basit bir bağlantılı düzlemsel grafiğe çokyüzlü grafik denir, eğer her bir tepe noktasının derecesi ≥ 3 ise, yani derece (V) ≥ 3 ∀ V ∈ G.

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |

Aynı yolu tekrar izlemeden tüm köşeler arasında bir yol çizebiliyorsanız, bir grafik çapraz geçiş yapılabilir. Bu yola dayanarak, bu bölümde açıklanan Euler'in yolu ve Euler'in devresi gibi bazı kategoriler vardır.

Euler'in Yolu

Bir Euler'in yolu, "G" nin her kenarını tam olarak bir kez ve "G" nin her köşesini en az bir kez içerir. Bağlı bir G grafiğinin, bir Euler'in yolunu içeriyorsa, çaprazlanabilir olduğu söylenir.

Example

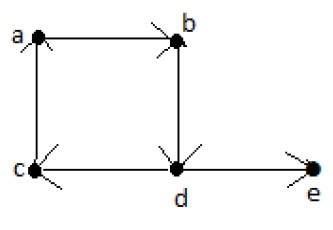
Euler'in Yolu = dcabde.

Euler Devresi

Bir Euler yolunda, başlangıç ​​noktası, bitiş noktasıyla aynıysa, buna bir Euler devresi denir.

Example

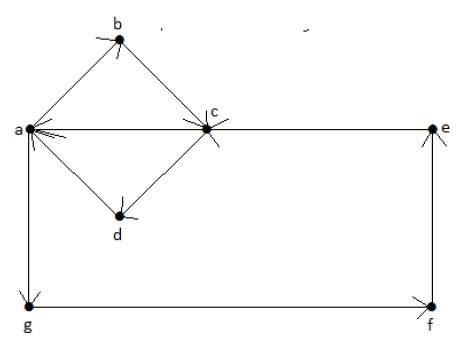
Euler’s Path = abcdagfeca.

Euler'in Devre Teoremi

Bağlantılı bir 'G' grafiği, ancak ve ancak G'de tek dereceli köşe sayısı tam olarak 2 veya 0 ise geçilebilir. garip bir derece.

Note - Bu Euler yolu, tek dereceli bir tepe noktasıyla başlar ve diğer tek dereceli tepe noktasıyla biter.

Example

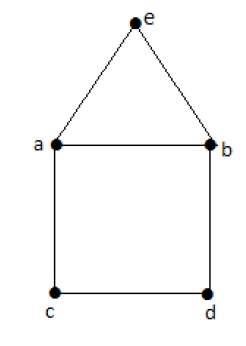
Euler’s Path- beabdca bir Euler'in devresi değil, bir Euler'in yoludur. Açıkça tam olarak 2 tek dereceli köşeye sahip.

Note - Bağlı bir G grafiğinde, tek dereceli köşe sayısı = 0 ise, Euler devresi vardır.

Hamilton Grafiği

G'nin tüm köşelerini içeren bir döngü varsa, bağlantılı bir G grafiğinin Hamilton grafiği olduğu söylenir.

Her döngü bir devredir ancak bir devre birden fazla döngü içerebilir. Böyle bir döngüye a denirHamiltonian cycle of G.

Hamilton Yolu

G'nin her tepe noktasını tam olarak bir kez içeriyorsa, bağlantılı bir grafiğin Hamiltonian olduğu söylenir. Böyle bir yola a denirHamiltonian path.

Example

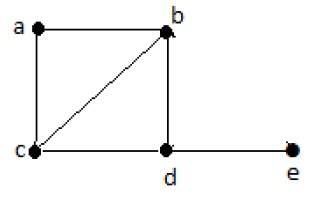
Hamiltonian Path- edbac.

Note

• Euler'in devresi, grafiğin her bir kenarını tam olarak bir kez içerir.

• Bir Hamilton döngüsünde, grafiğin bazı kenarları atlanabilir.

Example

Aşağıdaki grafiğe bir göz atın -

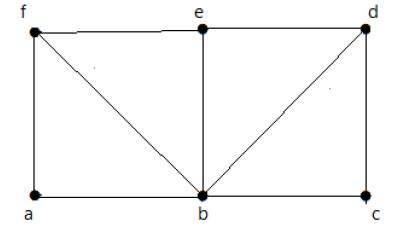
Yukarıda gösterilen grafik için -

• Euler yolu var - yanlış

• Euler devresi var - yanlış

• Hamilton döngüsü var - doğru

• Hamilton yolu var - doğru

G'nin tek dereceli dört köşesi vardır, bu nedenle geçilemez. İç kenarları atlayarak, grafik tüm köşelerden geçen bir Hamilton döngüsüne sahiptir.

Bu bölümde, daha önceki bölümlerde tartıştığımız kavramları göstermek için birkaç standart örneği ele alacağız.

örnek 1

Find the number of spanning trees in the following graph.

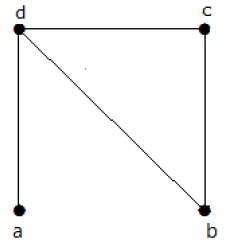
Çözüm

Yukarıdaki grafikten elde edilen yayılan ağaç sayısı 3'tür. Bunlar aşağıdaki gibidir -

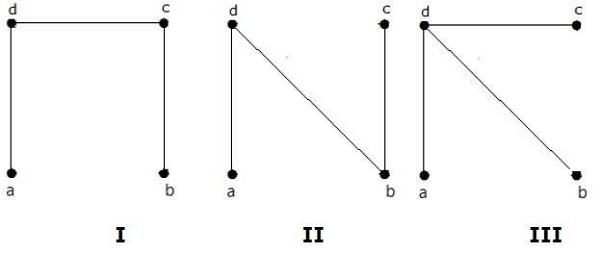
Bu üç, verilen grafikler için uzanan ağaçlardır. Burada I ve II grafikleri birbirine izomorftur. Açıkça, izomorfik olmayan yayılan ağaçların sayısı ikidir.

Örnek 2

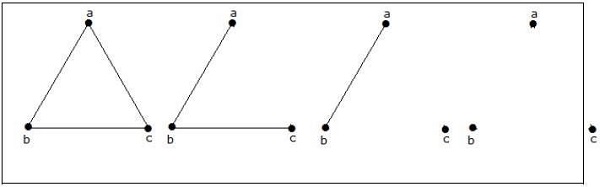
How many simple non-isomorphic graphs are possible with 3 vertices?

Çözüm

3 köşeli 4 izomorfik olmayan grafik mümkündür. Aşağıda gösterilmiştir.

Örnek 3

Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.

Çözüm

Derece teoreminin toplamına göre,

20 Σ i = 1 derece (Vi) = 2 | E |

20 (3) = 2 | E |

| E | = 30

Euler'in formülüne göre,

| V | + | R | = | E | + 2

20+ | R | = 30 + 2

| R | = 12

Dolayısıyla bölge sayısı 12'dir.

Örnek 4

What is the chromatic number of complete graph K_n?

Çözüm

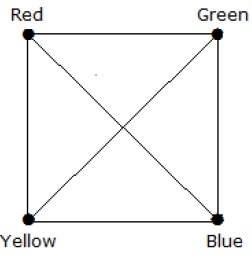
Tam bir grafikte, her köşe, kalan (n – 1) köşelere bitişiktir. Bu nedenle, her köşe için yeni bir renk gerekir. Dolayısıyla kromatik sayı K _n = n.

Örnek 5

What is the matching number for the following graph?

Çözüm

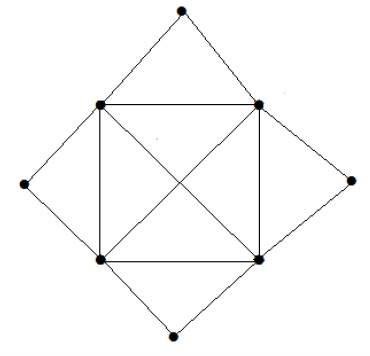
Köşe sayısı = 9

Yalnızca 8 köşeyi eşleştirebiliriz.

Eşleşen numara 4'tür.

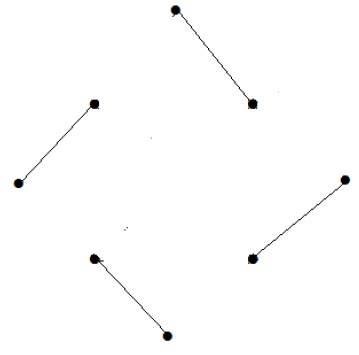
Örnek 6

What is the line covering number of for the following graph?

Çözüm

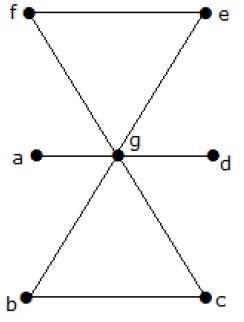
Köşe sayısı = | V | = n = 7

Satır kaplama numarası = (α ₁ ) ≥ [n / 2] = 3

α ₁ ≥ 3

3 kenar kullanarak tüm köşeleri kapatabiliriz.

Dolayısıyla satır kaplama numarası 3'tür.