Vũ trụ học - Khoảng cách đường kính góc
Trong chương này, chúng ta sẽ hiểu Khoảng cách Đường kính Góc là gì và nó giúp ích như thế nào trong Vũ trụ học.
Đối với vũ trụ hiện tại -
$ \ Omega_ {m, 0} \: = \: 0,3 $
$ \ Omega _ {\ wedge, 0} \: = \: 0,69 $
$ \ Omega_ {rad, 0} \: = \: 0,01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Chúng tôi đã nghiên cứu hai loại khoảng cách cho đến nay -
Proper distance (lp) - Khoảng cách mà các photon truyền từ nguồn đến chúng ta, tức là Instantaneous distance.
Comoving distance (lc) - Khoảng cách giữa các đối tượng trong một không gian không mở rộng, tức là distance in a comoving frame of reference.
Khoảng cách như một chức năng của Dịch chuyển đỏ
Hãy xem xét một thiên hà phát ra một photon tại một thời điểm t1 được phát hiện bởi người quan sát tại t0. Chúng ta có thể viết khoảng cách thích hợp đến thiên hà là -
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Hãy để dịch chuyển đỏ của thiên hà là z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ phân số {1} {a} $$
$$ \ do đó \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Bây giờ, khoảng cách di chuyển của thiên hà bất cứ lúc nào t sẽ là -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
Về mặt z,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Có hai cách để tìm khoảng cách, như sau:
Mối quan hệ Flux-Luminosity
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
Ở đâu d là khoảng cách tại nguồn.
Khoảng cách đường kính góc của nguồn
Nếu chúng ta biết kích thước của một nguồn, chiều rộng góc của nó sẽ cho chúng ta biết khoảng cách của nó với người quan sát.
$$ \ theta = \ frac {D} {l} $$
Ở đâu l là khoảng cách đường kính góc của nguồn.
θ là kích thước góc của nguồn.
D là kích thước của nguồn.
Hãy xem xét một thiên hà có kích thước D và kích thước góc dθ.
Chúng ta biết rằng,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ do đó D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ bởi vì dr ^ 2 = 0; \: d \ phi ^ 2 \ khoảng 0 $$
$$ \ Rightarrow D = a (t) rd \ theta $$
Thay đổi r đến rc, khoảng cách sắp đi của thiên hà, chúng ta có -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Đây, nếu chúng ta chọn t = t0, chúng tôi kết thúc việc đo khoảng cách hiện tại đến thiên hà. NhưngDđược đo tại thời điểm phát ra photon. Do đó, bằng cách sử dụngt = t0, chúng ta nhận được khoảng cách lớn hơn tới thiên hà và do đó đánh giá thấp kích thước của nó. Do đó, chúng ta nên sử dụng thời giant1.
$$ \ do đó d \ theta = \ frac {D} {r_ca (t_1)} $$
So sánh điều này với kết quả trước đó, chúng tôi nhận được -
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ bởi vì 1 + z_1 = \ frac {1} {a (t_1)} $$
Vì thế,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA là Khoảng cách Đường kính Góc cho đối tượng.
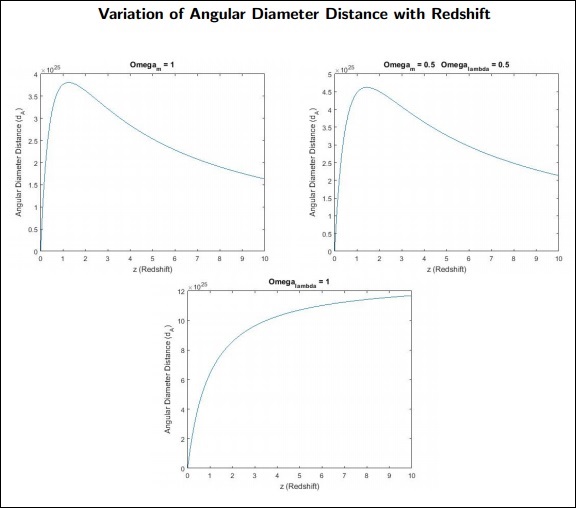
Những điểm cần nhớ
Nếu chúng ta biết kích thước của một nguồn, chiều rộng góc của nó sẽ cho chúng ta biết khoảng cách của nó với người quan sát.
Khoảng cách thích hợp là khoảng cách mà các photon truyền từ nguồn đến chúng ta.
Khoảng cách di chuyển là khoảng cách giữa các đối tượng trong một không gian không mở rộng.