Vũ trụ học - Phương pháp quá cảnh
Phương thức vận chuyển (Kepler Space Telescope)được sử dụng để tìm ra kích thước. Độ sáng của một ngôi sao bởi một hành tinh thường rất ít không giống như một hệ nhị phân.
F0 là dòng chảy của ngôi sao trước khi hành tinh xảy ra nó.
F1 là thông lượng sau khi toàn bộ hành tinh ở phía trước ngôi sao.
Hình ảnh sau đây sẽ được sử dụng cho tất cả các phép tính.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0,001 \% $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$
Điều này không dễ đạt được bằng kính thiên văn trên mặt đất. Nó đạt được nhờ kính thiên văn Hubble.

Ở đây, $ t_T $ là thời gian giữa vị trí A và D và $ t_F $ là thời gian giữa vị trí B và C.
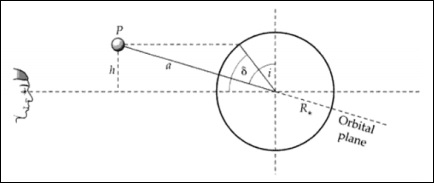
Hình dạng của phương tiện liên quan đến độ nghiêng icủa hệ thống. Vĩ độ và độ nghiêng chuyển tuyến có thể hoán đổi cho nhau.
Từ những hình ảnh trên, chúng ta có thể viết -
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
Ở đây, $ t_T $ là phần của khoảng thời gian mà quá trình chuyển tuyến xảy ra và (2θ / 2π) là phần nhỏ của góc mà quá trình chuyển tuyến xảy ra.
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Thông thường, a >> R ∗ >> Rp. Vì vậy, chúng ta có thể viết -
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Đây, Plà khoảng thời gian giữa hai lần chuyển tiếp liên tiếp. Thời gian vận chuyển rất ít hơn so với khoảng thời gian quỹ đạo. Vì thế,
$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$
Đây, tT, P, R∗ là những người có thể quan sát, a và i nên được tìm ra.
Hiện nay,
$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
trong đó, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.
Để cho,
$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$
Bây giờ, chúng ta có thể bày tỏ,
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
Đối với các ngôi sao của chuỗi chính,
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$
Điều này cho R∗.
Do đó, chúng tôi cũng nhận được giá trị của 'a'.
Vì vậy, chúng ta nhận được 'R p ', 'ap' và thậm chí là 'i'.
Cho tất cả điều này,
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
Đối với thậm chí ~ 89 độ, thời gian vận chuyển là rất nhỏ. Hành tinh phải ở rất gần để có đủ thời gian vận chuyển. Điều này tạo ra một hạn chế chặt chẽ đối với 'i'. Khi chúng ta nhận được 'i', chúng ta có thể suy ra 'm p ′ từ phép đo vận tốc xuyên tâm.
Việc phát hiện bằng phương pháp chuyển tuyến này được gọi là phát hiện cơ hội, tức là xác suất quan sát một tuyến đường. Các phép tính xác suất quá cảnh (xác suất quan sát) được hiển thị bên dưới
Xác suất chuyển tuyến liên quan đến góc vững chắc được xác định bởi hai cấu hình chuyển tuyến cực đoan, đó là -
$$ Solid \: angle \: of \: hành tinh \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$
Cũng như tổng góc đặc tại bán trục chính a, hoặc -
$$ Solid \: angle \: of \: bridge \: = \: 4 \ pi $$
Xác suất là tỷ lệ của hai khu vực này -
$$ = \: \ frac {area \: of \: sky \: che \: bởi \: thuận lợi \: hướng} {area \: of \: sky \: che \: bởi \: all \: có thể \: định hướng \: của \: quỹ đạo} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hidden \: cyclinder} {area \ : trong số \: hình cầu} $
Xác suất này không phụ thuộc vào người quan sát.
Những điểm cần nhớ
- Phương pháp Chuyển tuyến (Kính viễn vọng Không gian Kepler) được sử dụng để tìm ra kích thước.
- Phát hiện bằng Phương pháp chuyển tuyến là một phát hiện tình cờ.
- Hành tinh phải ở rất gần để có đủ thời gian vận chuyển.
- Xác suất chuyển tuyến liên quan đến góc rắn của hành tinh.
- Xác suất này không phụ thuộc vào hệ quy chiếu của người quan sát.