Vũ trụ học - Vũ trụ thống trị bức xạ
Trong chương này, chúng ta sẽ thảo luận về các Giải pháp cho Phương trình Friedmann liên quan đến Vũ trụ Chi phối Bức xạ. Lúc đầu, chúng ta so sánh mật độ năng lượng của vật chất với mật độ năng lượng của bức xạ. Điều này sẽ cho phép chúng ta biết được vũ trụ của chúng ta là vật chất chi phối hay bức xạ chi phối.
Mật độ năng lượng của bức xạ
Bức xạ phổ biến trong vũ trụ hiện nay có thể được cho là rất ít do các nguồn sao, mà chủ yếu là do CMB còn sót lại (Nền vi sóng vũ trụ).
Mật độ năng lượng của bức xạ, $ \ epsilon _ {\ gamma, 0} $, có thể được biểu thị như sau:
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$
Đây, a là hằng số bức xạ có biểu thức $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ bằng a = 7.5657 × 10−15erg\: cm−3 K−4. Nhiệt độ, T0, chúng ta xem xét ở đây, tương ứng với nhiệt độ của vật đen tương ứng với CMB.
Thay thế kết quả, chúng tôi có,
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} erg \: cm ^ {- 3} $$
Mật độ năng lượng của vật chất
Trong các phép tính sau, chúng ta có giả thiết làm việc với một vũ trụ phẳng và K = 0. Chúng ta coi mật độ năng lượng của vật chất là $ \ epsilon = \ rho c ^ 2 $. Chúng tôi xem xét những điều sau -
$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$
$$ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$
Như vậy, từ tính toán trên, chúng ta thấy rằng chúng ta đang sống trong một vũ trụ chi phối bởi vật chất. Điều này có thể được hỗ trợ bởi thực tế là CMB rất lạnh. Khi nhìn lại thời gian, chúng ta sẽ thấy nhiệt độ CMB trở nên nóng hơn, và có thể kết luận rằng có thể đã có một kỷ nguyên mà vũ trụ bị bức xạ chi phối.
Sự thay đổi của hệ số mật độ và tỷ lệ
Phương trình chất lỏng cho chúng ta thấy rằng -
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
Nếu chúng ta coi một vũ trụ đầy bụi, chúng ta sẽ có P = 0. Bỏ qua các kết quả trước đó, chúng ta coi vũ trụ như bị chi phối bởi bức xạ.
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
Sử dụng quan hệ áp suất của $ P_ {rad} = \ rho c ^ {2/3} $ ta có -
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$
Khi đơn giản hóa hơn nữa, chúng tôi có,
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$
$$ \ rho_ {rad} a ^ 4 = \: hằng $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
Kết quả chương trình trên một nghịch đảo 4 thứ biến sức mạnh của một bằng $ \ rho $.
Điều này có thể được hiểu về mặt vật lý là $ a ^ {- 3} $ đến từ sự thay đổi về khối lượng khi nó tăng lên. $ A ^ {- 1} $ còn lại có thể được coi là năng lượng mà photon bị mất đi do sự giãn nở của không gian trong vũ trụ (Dịch chuyển đỏ vũ trụ 1 + z = a -1 ).
Hình ảnh sau đây cho thấy sự biến thiên của vật chất và mật độ bức xạ theo thời gian.
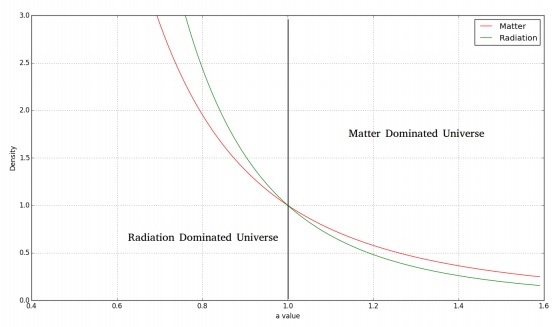
Đối với một vũ trụ phẳng, bức xạ chiếm ưu thế, chúng ta sẽ có phương trình Friedmann như sau:
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
Khi đơn giản hóa và áp dụng giải pháp cho phương trình vi phân, chúng ta có -
$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$
Do đó, chúng ta có -
$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$
Từ phương trình trên, chúng ta thấy rằng tốc độ gia tăng của hệ số tỷ lệ nhỏ hơn tốc độ gia tăng của vũ trụ bụi.
Những điểm cần nhớ
Bức xạ phổ biến trong vũ trụ hiện nay có thể được cho là rất ít từ các nguồn sao.
Đối với một vũ trụ đầy bụi, áp suất bằng không.
CMB rất lạnh lùng.