Vũ trụ học - Hướng dẫn nhanh

Cosmologylà nghiên cứu về vũ trụ. Truy ngược thời gian, có một số trường phái suy nghĩ về nguồn gốc của vũ trụ. Nhiều học giả tin vàoSteady State Theory. Theo lý thuyết này, vũ trụ luôn luôn giống nhau, nó không có khởi đầu.

Trong khi có một nhóm người tin vào Big Bang Theory. Lý thuyết này dự đoán sự khởi đầu của vũ trụ. Có bằng chứng về bức xạ nóng còn sót lại từ vụ nổ Big Bang, một lần nữa hỗ trợ mô hình. Lý thuyết Vụ nổ lớn dự đoán sự phong phú của các nguyên tố nhẹ trong vũ trụ. Do đó, theo mô hình nổi tiếng của Vụ nổ lớn, chúng ta có thể nói rằng vũ trụ đã có một sự khởi đầu. Chúng ta đang sống trong một vũ trụ đang giãn nở.

Dịch chuyển đỏ của Hubble

Vào đầu những năm 1900, kính thiên văn hiện đại, Mt Wilson, kính thiên văn 100 inch, là kính thiên văn lớn nhất khi đó. Hubble là một trong những nhà khoa học lỗi lạc, người đã làm việc với kính viễn vọng đó. Ông phát hiện ra có những thiên hà bên ngoài Dải Ngân hà.Extragalactic Astronomymới 100 tuổi. Mt Wilson là kính thiên văn lớn nhất cho đến khi Đài quan sát Palmer được xây dựng, nơi có kính thiên văn 200 inch.

Hubblekhông phải là người duy nhất quan sát các thiên hà bên ngoài Dải Ngân hà, Humason đã giúp anh ta. Họ bắt đầu đo quang phổ của các thiên hà gần đó. Sau đó, họ quan sát thấy một quang phổ thiên hà nằm trong dải bước sóng khả kiến ​​với sự phát xạ liên tục. Có các vạch phát xạ và hấp thụ trên đỉnh của liên tục. Từ những dòng này, chúng ta có thể ước tính xem thiên hà đang di chuyển ra xa chúng ta hay về phía chúng ta.

Khi chúng tôi nhận được quang phổ, chúng tôi giả định rằng vạch mạnh nhất đến từ H-α. Từ văn học, dòng mạnh nhất nên xảy ra ở6563 Å, nhưng nếu dòng xảy ra ở đâu đó xung quanh 7000Å, chúng ta có thể dễ dàng nói nó bị dịch chuyển đỏ.

Từ Special Theory of Relativity,

$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$

trong đó, Z là dịch chuyển đỏ, một số không thứ nguyên và v là vận tốc lùi.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {rest}} = 1 + z $$

Hubble và Humason được liệt kê xuống 22 Galaxiestrong bài báo của họ. Gần như tất cả các thiên hà này đều có hiện tượng dịch chuyển đỏ. Họ vẽ biểu đồ vận tốc (km / s) so với khoảng cách (Mpc). Họ đã quan sát một xu hướng tuyến tính và Hubble đã đưa ra định luật nổi tiếng của mình như sau.

$$ v_r = H_o d $$

Đây là Hubble Redshift Distance Relationship. Chỉ số dướircho biết sự mở rộng là theo hướng xuyên tâm. Trong khi, $ v_r $ là vận tốc rút lui, $ H_o $ là thông số Hubble,dlà khoảng cách của thiên hà với chúng ta. Họ kết luận rằng các thiên hà xa chúng ta rút lui nhanh hơn, nếu tốc độ giãn nở của vũ trụ là đồng đều.

Việc mở rộng

Mọi thứ đang rời xa chúng ta. Các thiên hà không đứng yên, luôn có một số điều hòa giãn nở. Các đơn vị của tham số Hubble là km giây ⁻¹ Mpc ⁻¹ . Nếu người ta đi ra ngoài một khoảng cách - 1 Mpc, các thiên hà sẽ chuyển động với tốc độ 200 km / giây. Tham số Hubble cho chúng ta biết tốc độ mở rộng. Theo Hubble và Humason, giá trị của $ H_o $ là 200 km / giây / Mpc.

Dữ liệu cho thấy tất cả các thiên hà đang di chuyển ra khỏi chúng ta. Như vậy, rõ ràng là chúng ta đang ở trung tâm của vũ trụ. Nhưng Hubble đã không mắc sai lầm này, theo ông ấy, trong bất kỳ thiên hà nào chúng ta đang sống, chúng ta sẽ thấy tất cả các thiên hà khác đang di chuyển ra khỏi chúng ta. Do đó, kết luận là không gian giữa các thiên hà giãn nở và không có trung tâm của vũ trụ.

Sự mở rộng đang diễn ra ở khắp mọi nơi. Tuy nhiên, có một số thế lực đang chống lại sự bành trướng. Liên kết hóa học, lực hấp dẫn và các lực hấp dẫn khác đang giữ các vật lại với nhau. Trước đó tất cả các đối tượng ở gần nhau. Coi Vụ nổ lớn là một lực xung động, các vật thể này chuyển động ra xa nhau.

Thang thời gian

Ở quy mô cục bộ, Động học được điều chỉnh bởi Trọng lực. Trong định luật Hubble ban đầu, có một số thiên hà cho thấy sự dịch chuyển màu xanh lam. Điều này có thể được cho là tiềm năng hấp dẫn tổng hợp của các thiên hà. Lực hấp dẫn đã tách mọi thứ ra khỏi định luật Hubble. Thiên hà Andromeda đang tiến về phía chúng ta. Trọng lực đang cố gắng làm mọi thứ chậm lại. Ban đầu việc mở rộng đang chậm lại, bây giờ nó đang được tăng tốc.

Có một Cosmic Jerkvì điều này. Một số ước tính cho thông số Hubble đã được thực hiện. Nó đã phát triển trong 90 năm từ 500 km / giây / Mpc lên 69 km / giây / Mpc. Sự chênh lệch về giá trị là do khoảng cách bị đánh giá thấp. CácCepheid Stars được sử dụng làm máy hiệu chuẩn khoảng cách, tuy nhiên có nhiều loại sao Cepheid khác nhau và thực tế này không được xem xét để ước tính tham số Hubble.

Giờ Hubble

Hằng số Hubble cho chúng ta ước tính thực tế về tuổi của vũ trụ. $ H_o $ sẽ cho biết tuổi của vũ trụ với điều kiện các thiên hà chuyển động với cùng một vận tốc. Nghịch đảo của $ H_o $ cho chúng ta thời gian Hubble.

$$ t_H = \ frac {1} {H_o} $$

Thay thế giá trị hiện tại của $ H_o, t_H $ = 14tỷ năm. Tốc độ mở rộng không đổi trong suốt thời kỳ đầu của Vũ trụ. Ngay cả khi điều này không đúng, $ H_o $ đưa ra một giới hạn hữu ích về tuổi của vũ trụ. Giả sử tốc độ giãn nở không đổi, khi chúng ta vẽ đồ thị giữa quãng đường và thời gian, độ dốc của đồ thị được cho bởi vận tốc.

Trong trường hợp này, thời gian của Hubble bằng với thời gian thực. Tuy nhiên, nếu vũ trụ giãn nở nhanh hơn trong quá khứ và chậm hơn trong hiện tại, thì thời gian Hubble đưa ra giới hạn trên của tuổi vũ trụ. Nếu trước đây vũ trụ giãn nở chậm và hiện tại đang tăng tốc, thì thời gian Hubble sẽ đưa ra giới hạn thấp hơn về tuổi của vũ trụ.

• $ t_H = t_ {age} $ - nếu tốc độ mở rộng không đổi.

• $ t_H> t_ {age} $ - nếu vũ trụ giãn nở nhanh hơn trong quá khứ và chậm hơn trong hiện tại.

• $ t_H <t_ {age} $ - nếu vũ trụ giãn nở chậm hơn trong quá khứ và nhanh hơn trong hiện tại.

Hãy xem xét một nhóm gồm 10 thiên hà có tốc độ 200 Mpc từ một nhóm thiên hà khác. Các thiên hà trong một cụm không bao giờ kết luận rằng vũ trụ đang giãn nở bởi vì động học trong một nhóm cục bộ bị chi phối bởi lực hấp dẫn.

Những điểm cần nhớ

• Vũ trụ học là nghiên cứu về quá khứ, hiện tại và tương lai của Vũ trụ của chúng ta.

• Vũ trụ của chúng ta đã ∼14 tỷ năm tuổi.

• Vũ trụ không ngừng giãn nở.

• Tham số Hubble là thước đo tuổi của vũ trụ.

• Giá trị hiện tại của H_o là 69 km / giây / Mpc.

Trong một thời gian rất dài, không ai coi các thiên hà hiện diện bên ngoài Dải Ngân hà của chúng ta. Năm 1924, Edwin Hubble phát hiệnCepheid’strong Tinh vân Tiên nữ và ước tính khoảng cách của chúng. Ông kết luận rằng những "Tinh vân Xoắn ốc" này thực chất là các thiên hà khác và không phải là một phần của Dải Ngân hà của chúng ta. Do đó, ông cho rằng M31 (Thiên hà Tiên nữ) là một Đảo vũ trụ. Đây là sự ra đời củaExtragalactic Astronomy.

Cepheid's cho thấy một periodic dip in their brightness. Các quan sát cho thấy rằng khoảng thời gian giữa các lần lặn liên tiếp được gọi là chu kỳ xung có liên quan đến độ sáng. Vì vậy, chúng có thể được sử dụng làm chỉ số khoảng cách. Các ngôi sao thuộc dãy chính như Mặt trời đang ở trạng thái Cân bằng thủy tĩnh và chúng đốt cháy hydro trong lõi của chúng. Sau khi hydro được đốt cháy hoàn toàn, các ngôi sao di chuyển về phía Pha Khổng lồ Đỏ và cố gắng lấy lại trạng thái cân bằng.

Các ngôi sao Cepheid là các ngôi sao của Chuỗi chính đang chuyển tiếp từ các ngôi sao của Chuỗi chính sang Sao khổng lồ đỏ.

Phân loại Cepheids

Có 3 lớp rộng của các sao biến đổi xung động này -

• Type-I Cepheids (hoặc Cepheids Cổ điển) - khoảng thời gian 30-100 ngày.

• Type-II Cepheids (hoặc W Virginis Stars) - khoảng thời gian từ 1-50 ngày.

• RR Lyrae Stars - khoảng thời gian 0,1-1 ngày.

Vào thời điểm đó, Hubble không biết về sự phân loại các sao biến thiên này. Đó là lý do tại sao đã có sự đánh giá quá mức về hằng số Hubble, do đó ông ước tính tuổi vũ trụ của chúng ta thấp hơn. Vì vậy, tốc độ suy thoái cũng được đánh giá quá cao. Trong Cepheid's, nhiễu động lan truyền hướng tâm ra ngoài từ tâm của ngôi sao cho đến khi đạt được trạng thái cân bằng mới.

Mối liên quan giữa độ sáng và thời kỳ xung đột

Bây giờ chúng ta hãy thử tìm hiểu cơ sở vật lý của thực tế là chu kỳ xung cao hơn có nghĩa là độ sáng nhiều hơn. Xét một ngôi sao có độ sáng L và khối lượng M.

Chúng tôi biết rằng -

$$ L \ propto M ^ \ alpha $$

trong đó α = 3 đến 4 đối với sao khối lượng thấp.

Từ Stefan Boltzmann Law, chúng tôi biết rằng -

$$ L \ propto R ^ 2 T ^ 4 $$

Nếu R là bán kính và $ c_s $ là tốc độ âm thanh, sau đó là chu kỳ dao động P có thể được viết là -

$$ P = R / c_s $$

Nhưng tốc độ của âm thanh qua bất kỳ phương tiện nào có thể được biểu thị theo nhiệt độ như -

$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$

Đây, γ là 1 đối với trường hợp đẳng nhiệt.

Đối với khí lý tưởng, P = nkT, trong đó k là Boltzmann Constant. Vì vậy, chúng ta có thể viết -

$$ P = \ frac {\ rho kT} {m} $$

trong đó $ \ rho $ là mật độ và m là khối lượng của một proton.

Do đó, khoảng thời gian được cho bởi -

$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT) ^ {{\ frac {1} {2}}}} $$

Virial Theorem cho biết rằng đối với sự phân bố ổn định, tự hấp dẫn, hình cầu của các vật thể khối lượng bằng nhau (như các ngôi sao, thiên hà) thì tổng động năng k của vật bằng trừ một nửa tổng thế năng trọng trường u, I E,

$$ u = -2k $$

Chúng ta hãy giả sử rằng định lý virial đúng với những ngôi sao biến thiên này. Nếu chúng ta xem xét một proton ngay trên bề mặt của ngôi sao, thì từ định lý virial, chúng ta có thể nói:

$$ \ frac {GMm} {R} = mv ^ 2 $$

Từ phân phối Maxwell,

$$ v = \ sqrt {\ frac {3kT} {2}} $$

Do đó, kỳ -

$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM) ^ {\ frac {1} {2}}} $$

ngụ ý

$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$

Chúng tôi biết rằng - $ M \ propto L ^ {1 / \ alpha} $

Ngoài ra $ R \ propto L ^ {1/2} $

Vì vậy đối với β > 0, cuối cùng chúng tôi nhận được - $ P \ propto L ^ \ beta $

Những điểm cần nhớ

• Các ngôi sao Cepheid là các ngôi sao của Chuỗi chính đang chuyển đổi từ các ngôi sao của Chuỗi chính sang Người khổng lồ đỏ.

• Cepheid có 3 loại: Loại I, Loại II, RR-Lyrae theo thứ tự giảm dần của chu kỳ xung.

• Thời gian tạo nhũ của Cepheid tỷ lệ thuận với độ sáng (độ sáng) của nó.

Các quan sát của Hubble đã sử dụng thực tế rằng vận tốc hướng tâm có liên quan đến sự dịch chuyển của Spectral Lines. Ở đây, chúng ta sẽ quan sát bốn trường hợp và tìm mối quan hệ giữa Vận tốc nghỉ ($ v_r $) và Red Shift (z).

Trường hợp 1: Trường hợp không tương đối tính của nguồn di chuyển

Trong trường hợp này, v nhỏ hơn nhiều so với c. Nguồn đang phát ra một số tín hiệu (âm thanh, ánh sáng, v.v.), đang lan truyền nhưWavefronts. Khoảng thời gian giữa lúc gửi hai tín hiệu liên tiếp trong khung nguồn làΔts. Khoảng thời gian giữa lúc thu được hai tín hiệu liên tiếp trong khung người quan sát làΔto.

Nếu cả người quan sát và nguồn đều đứng yên, thì Δts = Δto, nhưng đây không phải là trường hợp. Thay vào đó, mối quan hệ như sau.

$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$

Bây giờ, $ \ Delta l = v \ Delta t_s $

Ngoài ra, vì (tốc độ sóng x thời gian) = bước sóng, chúng ta nhận được

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$

Từ các phương trình trên, chúng ta nhận được quan hệ sau:

$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$

trong đó $ \ lambda _s $ là bước sóng của tín hiệu tại nguồn và $ \ lambda _o $ là bước sóng của tín hiệu được người quan sát giải thích.

Ở đây, vì nguồn đang di chuyển ra khỏi người quan sát, v tích cực.

Ca đỏ -

$$ z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1 $$

Từ các phương trình trên, chúng ta nhận được dịch chuyển Đỏ như sau.

$$ z = \ frac {v} {c} $$

Trường hợp 2: Trường hợp không tương đối tính của người quan sát di chuyển

Trong trường hợp này, v nhỏ hơn nhiều so với c. Ở đây, $ \ Delta l $ thì khác.

$$ \ Delta l = v \ Delta t_o $$

Khi đơn giản hóa, chúng tôi nhận được -

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1} $$

Chúng tôi nhận được Red shift như sau:

$$ z = \ frac {v / c} {1-v / c} $$

Từ v << c, biểu thức dịch chuyển màu đỏ cho cả Trường hợp I và Trường hợp II là gần giống nhau.

Chúng ta hãy xem dịch chuyển màu đỏ thu được trong hai trường hợp trên khác nhau như thế nào.

$$ z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right] $$

Do đó, $ z_ {II} - z_ {I} $ là một số rất nhỏ do hệ số $ (v / c) ^ 2 $.

Điều này ngụ ý rằng, nếu v << c, chúng ta không thể biết nguồn đang chuyển động hay người quan sát đang chuyển động.

Bây giờ chúng ta hãy hiểu Basics of STR (Thuyết tương đối hẹp) -

• Tốc độ ánh sáng là một hằng số.

• Khi nguồn (hoặc người quan sát) đang chuyển động với tốc độ tương đương với tốc độ ánh sáng, các hiệu ứng tương đối tính được quan sát thấy.

• Thời gian giãn nở: $ \ Delta t_o = \ gamma \ Delta t_s $

• Độ dài thu hẹp: $ \ Delta l_o = \ Delta t_s / \ gamma $

• Đây, $ \ gamma $ là Lorrentz factor, lớn hơn 1.

$$ \ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Trường hợp 3: Trường hợp tương đối tính của chuyển nguồn

Trong trường hợp này, v có thể so sánh với c. Tham khảo hình tương tự như trong Trường hợp I. Do hiệu ứng tương đối tính, sự giãn nở thời gian được quan sát và do đó thu được quan hệ sau. (Nguồn đang di chuyển với tốc độ tương đối tính)

$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Khi đơn giản hóa hơn nữa, chúng tôi nhận được,

$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$

Biểu thức trên được gọi là Kinematic Doppler Shift Expression.

Trường hợp 4: Trường hợp tương đối tính của người quan sát di chuyển

Tham khảo hình tương tự như trong Trường hợp II. Do hiệu ứng tương đối tính, sự rút ngắn thời gian được quan sát và do đó có được quan hệ sau. (Người quan sát đang di chuyển với tốc độ tương đối tính)

$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c} $$

Khi đơn giản hóa hơn nữa, chúng tôi nhận được -

$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$

Biểu thức trên giống như những gì chúng ta nhận được cho Trường hợp III.

Những điểm cần nhớ

• Vận tốc kỳ hạn và dịch chuyển đỏ của một ngôi sao là các đại lượng liên quan.

• Trong trường hợp không tương đối tính, chúng ta không thể xác định nguồn đang chuyển động hay đứng yên.

• Trong trường hợp tương đối tính, không có sự khác biệt trong mối quan hệ vận tốc dịch chuyển đỏ-lõm đối với nguồn hoặc vật quan sát chuyển động.

• Đồng hồ chuyển động di chuyển chậm hơn, là kết quả trực tiếp của thuyết tương đối.

Một thiên hà ở dịch chuyển đỏ z = 10, tương ứng với v≈80% của c. Khối lượng của Dải Ngân hà xung quanh1011M⊙, nếu chúng ta xem xét vật chất tối, nó là 1012M⊙. Con đường sữa của chúng ta do đó rất lớn. Nếu nó di chuyển ở 80%c, nó không phù hợp với khái niệm chung về cách các đối tượng chuyển động.

Chúng tôi biết,

$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda {rest}} {\ lambda_ {rest}} $$

Đối với các giá trị nhỏ của z,

$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda_ {rest}} {\ lambda_ {rest}} $$

Trong đồ thị sau đây, phân lớp giữa thông lượng và bước sóng, có các vạch phát xạ trên đỉnh của liên tục. TừH-α thông tin dòng, chúng tôi có thể kết luận rằng đại khái z = 7. Điều này ngụ ý rằng thiên hà đang di chuyển với 70%c. Chúng tôi đang quan sát một sự thay đổi và giải thích nó là vận tốc. Chúng ta nên loại bỏ quan niệm này và nhìn vàoztheo một cách khác. Hãy tưởng tượng không gian như một lưới 2D đại diện cho vũ trụ như hình dưới đây.

Hãy coi ngôi sao đen là dải ngân hà của chúng ta và ngôi sao xanh là một thiên hà khác. Khi chúng ta ghi lại ánh sáng từ thiên hà này, chúng ta nhìn thấy quang phổ và tìm ra dịch chuyển đỏ của nó, tức là thiên hà đang di chuyển ra xa. Khi photon được phát ra, nó có vận tốc tương đối.

• Điều gì sẽ xảy ra nếu không gian được mở rộng?

• Nó là một sự dịch chuyển đỏ tức thời của photon. Dịch chuyển đỏ tích lũy dọc theo không gian giữa hai thiên hà sẽ có xu hướng dịch chuyển đỏ lớn. Bước sóng sẽ thay đổi cuối cùng. Đó là sự giãn nở của không gian chứ không phải là chuyển động động học của các thiên hà.

Hình ảnh sau đây cho thấy nếu lực hấp dẫn lẫn nhau tràn qua sự giãn nở thì điều này không tham gia vào định luật Hubble.

Trong Chuyển dịch Doppler Động học, dịch chuyển đỏ được tạo ra trong một photon tại thời điểm phát xạ. Trong Dịch chuyển Đỏ vũ trụ, trong mỗi bước, nó đang bị dịch chuyển đỏ tích lũy. Trong thế năng hấp dẫn, một photon sẽ bị dịch chuyển màu xanh lam. Khi nó bò ra khỏi thế năng hấp dẫn, nó sẽ bị dịch chuyển đỏ.

Theo Thuyết tương đối hẹp, hai vật thể đi ngang qua nhau không thể có vận tốc tương đối lớn hơn vận tốc ánh sáng. Vận tốc mà chúng ta nói đến là sự giãn nở của vũ trụ. Đối với các giá trị lớn của z, dịch chuyển đỏ là vũ trụ học và không phải là một phép đo hợp lệ của vận tốc lặn thực tế của vật thể đối với chúng ta.

Nguyên lý vũ trụ

Nó bắt nguồn từ Copernicus Notioncủa vũ trụ. Theo quan niệm này, vũ trụ là đồng nhất và đẳng hướng. Không có hướng và vị trí ưa thích trong vũ trụ.

• Đồng nhất có nghĩa là bất kể bạn cư trú ở phần nào của vũ trụ, bạn sẽ thấy vũ trụ giống nhau ở tất cả các phần. Tính chất đẳng hướng có nghĩa là bất kể bạn nhìn theo hướng nào, bạn sẽ thấy cùng một cấu trúc.

• Một ví dụ phù hợp về tính đồng nhất là cánh đồng Lúa. Nó trông đồng nhất từ ​​tất cả các bộ phận, nhưng khi gió chảy, có những thay đổi về hướng của nó, do đó nó không phải là đẳng hướng. Xét một ngọn núi trên một vùng đất bằng phẳng và một người quan sát đang đứng trên đỉnh núi. Anh ta sẽ thấy tính chất đẳng hướng của vùng đất bằng phẳng, nhưng nó không đồng nhất. Nếu trong một vũ trụ đồng nhất, nó là đẳng hướng tại một điểm, thì nó là đẳng hướng ở mọi nơi.

• Đã có những cuộc khảo sát quy mô lớn để lập bản đồ vũ trụ. Sloan Digital Sky Surveylà một trong những cuộc khảo sát như vậy, không tập trung nhiều vào sự xuống dốc, nhưng vào đúng sự thăng thiên. Thời gian nhìn lại là khoảng 2 tỷ năm. Mỗi pixel tương ứng với vị trí của một thiên hà và màu sắc tương ứng với cấu trúc hình thái học. Màu xanh lục biểu thị thiên hà xoắn ốc màu xanh lam trong khi màu giả màu đỏ biểu thị các thiên hà lớn.

• Các thiên hà có cấu trúc dạng sợi trong mạng vũ trụ và có những khoảng trống ở giữa các thiên hà.

• $ \ delta M / M \ cong 1 $ tức là sự dao động của phân bố khối lượng là 1 M là khối lượng của vật chất có trong một hình lập phương nhất định. Trong trường hợp này, lấy khối lập phương 50 Mpc.

• Đối với mặt lập phương có kích thước 1000 Mpc, $ \ delta M / M \ cong 10 ^ {- 4} $.

• Một cách để định lượng độ đồng nhất là lấy dao động khối lượng. Biến động khối lượng sẽ cao hơn ở các quy mô thấp hơn.

• Để định lượng bản chất đẳng hướng, hãy xem xét bức xạ phông vi sóng vũ trụ. Vũ trụ gần như đẳng hướng ở quy mô góc lớn.

Những điểm cần nhớ

• Hai vật đi ngang qua nhau không thể có vận tốc tương đối lớn hơn vận tốc ánh sáng.

• Nguyên lý vũ trụ phát biểu rằng vũ trụ là đồng nhất và đẳng hướng.

• Sự đồng nhất này tồn tại ở quy mô góc rất lớn chứ không phải ở quy mô nhỏ hơn.

• SDSS (Khảo sát Bầu trời Kỹ thuật số Sloan) là một nỗ lực lập bản đồ bầu trời đêm, xác minh Nguyên lý Vũ trụ.

Theo định luật bảo toàn năng lượng và định luật bảo toàn khối lượng, tổng năng lượng bao gồm cả khối lượng (E = mc ² ) không thay đổi trong mọi bước của bất kỳ quá trình nào trong vũ trụ. Bản thân sự giãn nở của vũ trụ tiêu thụ năng lượng có thể từ sự kéo dài bước sóng của các photon (Dịch chuyển đỏ vũ trụ), Tương tác năng lượng tối, v.v.

Để tăng tốc độ khảo sát hơn 26.000 thiên hà, Stephen A. Shectmanđã thiết kế một công cụ có khả năng đo đồng thời 112 thiên hà. Trong một tấm kim loại, người ta khoan các lỗ tương ứng với vị trí của các thiên hà trên bầu trời. Các dây cáp quang mang ánh sáng từ mỗi thiên hà xuống một kênh riêng biệt trên máy quang phổ tại kính thiên văn du Pont dài 2,5 mét tạiCarnegie Observatories trên Cerro Las Campanas ở Chile.

Để đạt hiệu quả tối đa, một kỹ thuật chuyên biệt được gọi là Drift-Scan Photometryđã được sử dụng, trong đó kính viễn vọng được hướng vào đầu của một trường khảo sát và sau đó ổ đĩa tự động bị tắt. Kính viễn vọng đứng yên khi bầu trời trôi qua. Máy tính đọc thông tin từCCD Detectorvới cùng tốc độ quay của trái đất, tạo ra một hình ảnh dài, liên tục ở một vĩ độ thiên thể không đổi. Việc hoàn thành phép đo quang mất tổng cộng 450 giờ.

Các dạng nhiễu khác nhau tồn tại và mô hình toán học của chúng cũng khác nhau tùy thuộc vào tính chất của nó. Các quá trình vật lý khác nhau phát triển phổ sức mạnh của vũ trụ trên quy mô lớn. Phổ công suất ban đầu được truyền do các dao động lượng tử theo sau công suất âm thứ ba của tần số là một dạng củaPink Noise Spectrum trong không gian ba chiều.

Chỉ số

Trong vũ trụ học, trước tiên người ta phải có một định nghĩa về không gian. Số liệu là một biểu thức toán học mô tả các điểm trong không gian. Việc quan sát bầu trời được thực hiện dưới dạng hình cầu; do đó một hệ tọa độ cầu sẽ được sử dụng. Khoảng cách giữa hai điểm gần nhau được cho bởi:

$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$

Hình ảnh sau đây cho thấy Hình học trong không gian Euclid 3 chiều không mở rộng.

Hình học này vẫn nằm trong không gian Euclid 3 chiều không giãn nở. Do đó, lưới tham chiếu xác định chính khung sẽ được mở rộng. Hình ảnh sau đây mô tả số liệu tăng lên.

Một yếu tố tỷ lệ được đưa vào phương trình của không gian không giãn nở, được gọi là 'yếu tố tỷ lệ' kết hợp sự giãn nở của vũ trụ theo thời gian.

$$ ds ^ 2 = a ^ 2 (t) \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$

Ở đâu a(t) là hệ số tỷ lệ, đôi khi được viết là R(t). Trong khi,a(t) > 1 có nghĩa là độ phóng đại của chỉ số, trong khi a(t) < 1 có nghĩa là thu hẹp số liệu và a(t) = 1nghĩa là số liệu không đổi. Như một quy ước,a(t₀) = 1.

Hệ tọa độ đi lại

Trong một Comoving Coordinate System, thang đo giãn nở cùng với khung (vũ trụ giãn nở).

Ở đây, $ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $ là Khoảng cách Di chuyển và $ ds ^ 2 $ là Khoảng cách thích hợp.

Khoảng cách thích hợp sẽ tương ứng với khoảng cách thực tế được đo của một thiên hà xa trái đất tại thời điểm quan sát, hay còn gọi là khoảng cách tức thời của các vật thể.

Điều này là do khoảng cách di chuyển của một photon khi nó đến người quan sát từ một nguồn ở xa sẽ là khoảng cách nhận được tại $ t = t_0 $ của người quan sát, có nghĩa là khoảng cách quan sát tức thời sẽ là khoảng cách thích hợp, và người ta có thể dự đoán khoảng cách trong tương lai bằng cách sử dụng hệ số tốc độ và độ dài đo được ban đầu làm tham chiếu.

Khái niệm Đi lại và khoảng cách thích hợp rất quan trọng trong việc đo giá trị thực tế của mật độ số lượng thiên hà trong thể tích nhất định của không gian quan sát. Người ta phải sử dụng Khoảng cách đi lại để tính toán mật độ tại thời điểm hình thành của chúng khi photon quan sát được phát ra. Điều đó có thể đạt được sau khi ước tính được tốc độ giãn nở của vũ trụ.

Để ước tính tốc độ giãn nở, người ta có thể quan sát sự thay đổi khoảng cách của một thiên hà xa xôi quan sát được trong một khoảng thời gian dài.

Những điểm cần nhớ

• Số liệu là một biểu thức toán học mô tả các điểm trong không gian.

• Yếu tố tỷ lệ xác định xem vũ trụ đang co lại hay đang giãn nở.

• Trong một hệ tọa độ đi lại, thang đo mở rộng cùng với khung (vũ trụ giãn nở).

• Khoảng cách thích hợp là khoảng cách tức thời của các vật.

• Khoảng cách di chuyển là khoảng cách thực tế của các đối tượng.

Trong chương này, chúng ta sẽ hiểu chi tiết về Chỉ số Robertson-Walker.

Mô hình cho yếu tố quy mô thay đổi theo thời gian

Giả sử một photon được phát ra từ một thiên hà xa xôi. Không gian chuyển tiếp cho photon theo mọi hướng. Sự giãn nở của vũ trụ theo tất cả các hướng. Hãy để chúng tôi xem hệ số tỷ lệ thay đổi như thế nào theo thời gian trong các bước sau.

Step 1 - Đối với vũ trụ tĩnh, hệ số tỷ lệ là 1, tức là giá trị của khoảng cách đi lại là khoảng cách giữa các đối tượng.

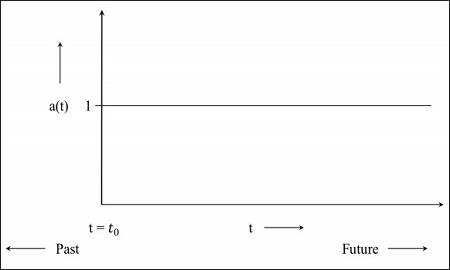
Step 2- Hình ảnh sau đây là đồ thị của vũ trụ vẫn đang giãn nở nhưng với tốc độ giảm dần, có nghĩa là đồ thị sẽ bắt đầu trong quá khứ. Cáct = 0 chỉ ra rằng vũ trụ bắt đầu từ thời điểm đó.

Step 3 - Hình ảnh sau đây là đồ thị cho vũ trụ đang giãn nở với tốc độ nhanh hơn.

Step 4 - Hình ảnh sau đây là đồ thị cho vũ trụ bắt đầu co lại từ bây giờ.

Nếu giá trị của hệ số tỷ lệ trở thành 0 trong sự co lại của vũ trụ, nó ngụ ý khoảng cách giữa các vật thể trở nên 0, tức là khoảng cách thích hợp trở thành 0. Khoảng cách đi tới là khoảng cách giữa các vật thể tại một vũ trụ hiện tại, là một đại lượng không đổi. Trong tương lai, khi yếu tố quy mô trở thành0, mọi thứ sẽ đến gần hơn. Mô hình phụ thuộc vào thành phần của vũ trụ.

Số liệu cho vũ trụ giãn nở phẳng (Euclide: không có tham số cho độ cong) được đưa ra là:

$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$

Đối với không gian - thời gian, phần tử đường mà chúng ta thu được trong phương trình trên được sửa đổi thành:

$$ ds ^ 2 = c ^ 2dt ^ 2 - \ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) \ right \} $$

Đối với không - thời gian, thời gian mà photon được phát ra và khi nó được phát hiện là khác nhau. Khoảng cách thích hợp là khoảng cách tức thời đến các vật thể có thể thay đổi theo thời gian do sự giãn nở của vũ trụ. Đó là khoảng cách mà photon đã di chuyển từ các vật thể khác nhau để đến được với chúng ta. Nó liên quan đến khoảng cách di chuyển là -

$$ d_p = a (t) \ times d_c $$

trong đó $ d_p $ là khoảng cách thích hợp và $ d_c $ là khoảng cách đi kèm, được cố định.

Khoảng cách đo được đến các vật thể trong vũ trụ hiện tại được coi là khoảng cách đi tới, có nghĩa là khoảng cách đi tới là cố định và không thay đổi khi giãn nở. Trước đây, hệ số tỷ lệ nhỏ hơn 1, điều này cho thấy khoảng cách thích hợp nhỏ hơn.

Chúng ta có thể đo độ lệch đỏ của một thiên hà. Do đó, khoảng cách thích hợp $ d_p $ tương ứng với $ c \ times t (z) $, trong đó $ t (z) $ là thời gian nhìn lại đối với dịch chuyển đỏ và c là tốc độ ánh sáng trong chân không. Thời gian xem lại là một hàm của dịch chuyển đỏ(z).

Dựa trên khái niệm trên, chúng ta hãy phân tích cách dịch chuyển đỏ vũ trụ được diễn giải trong kịch bản $ d_p = a (t) \ times d_c $.

Giả sử một photon (liên kết trái đất) được phát ra bởi thiên hà G. $ t_ {em} $ tương ứng với thời gian photon được phát ra; $ a (t_ {em}) $ là hệ số tỷ lệ tại thời điểm đó khi photon được phát ra. Vào thời điểm phát hiện ra photon, toàn bộ vũ trụ đã mở rộng, tức là photon bị dịch chuyển đỏ tại thời điểm phát hiện. $ T_ {obs} $ tương ứng với thời điểm phát hiện ra photon và hệ số tỷ lệ tương ứng là $ a (t_ {obs}) $.

Yếu tố mà vũ trụ phát triển được đưa ra bởi -

$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$

Hệ số mà bước sóng đã mở rộng là -

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

bằng với hệ số mà vũ trụ đã phát triển. Các biểu tượng có ý nghĩa thông thường của chúng. Vì thế,

$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

Chúng tôi biết rằng dịch chuyển đỏ (z) là -

$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$

$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$

Giá trị hiện tại của hệ số tỷ lệ là 1, do đó $ a (t_ {obs}) = 1 $ và biểu thị hệ số tỷ lệ khi photon được phát ra trong quá khứ là $ a (t) $.

Vì thế,

$$ 1 + z = \ frac {1} {a (t)} $$

Giải thích Dịch chuyển Đỏ trong Vũ trụ học

Để hiểu điều này, chúng ta hãy lấy ví dụ sau: Nếu $ z = 2 $ thì $ a (t) = 1/3 $.

Nó ngụ ý rằng vũ trụ đã mở rộng thêm ba lần kể từ khi ánh sáng rời khỏi vật thể đó. Bước sóng của bức xạ nhận được đã mở rộng theo hệ số ba vì không gian đã mở rộng theo cùng một hệ số trong quá trình truyền từ vật thể phát ra. Cần lưu ý rằng ở các giá trị lớn như vậy củaz, dịch chuyển đỏ chủ yếu là dịch chuyển đỏ vũ trụ, và nó không phải là thước đo hợp lệ về vận tốc lặn thực tế của vật thể đối với chúng ta.

Đối với nền vi sóng vũ trụ (CMB), z = 1089, có nghĩa là vũ trụ hiện tại đã mở rộng bởi một yếu tố ∼1090. Số liệu cho vũ trụ phẳng, Euclid, đang giãn nở được đưa ra là -

$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$

Chúng tôi muốn viết số liệu theo bất kỳ độ cong nào.

Robertson and Walker được chứng minh cho bất kỳ vũ trụ cong nào (đồng nhất và đẳng hướng), số liệu được cho là:

$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$

Điều này thường được gọi là Robertson–Walker Metricvà đúng với bất kỳ cấu trúc liên kết nào của không gian. Xin lưu ý hệ số phụ trong $ dr ^ 2 $. Đây là hằng số độ cong.

Hình học của vũ trụ

Hình học của Vũ trụ được giải thích với sự trợ giúp của các Đường cong sau đây, bao gồm:

• Độ cong dương
• Độ cong âm
• Độ cong bằng không

Hãy để chúng tôi hiểu chi tiết từng điều này.

Độ cong dương

Nếu một mặt phẳng tiếp tuyến được vẽ tại bất kỳ điểm nào trên bề mặt cong mà không cắt nhau tại bất kỳ điểm nào trên bề mặt, nó được gọi là bề mặt có độ cong dương tức là bề mặt nằm trên một phía của mặt phẳng tiếp tuyến tại điểm đó. Mặt cầu có độ cong dương.

Độ cong âm

Nếu một mặt phẳng tiếp tuyến được vẽ tại một điểm trên bề mặt cong cắt nhau tại bất kỳ điểm nào trên bề mặt, nó được gọi là bề mặt có độ cong âm tức là bề mặt đó cong ra khỏi mặt phẳng tiếp tuyến theo hai hướng khác nhau. Bề mặt hình yên ngựa có độ cong âm.

Bây giờ hãy xem xét bề mặt của một hình cầu. Nếu một tam giác được xây dựng trên bề mặt của hình cầu bằng cách nối ba điểm với đường trắc địa (cung của các đường tròn lớn), thì tổng các góc bên trong của tam giác hình cầu lớn hơn 180 ^o , tức là -

$$ \ alpha + \ beta + \ gamma> \ pi $$

Không gian như vậy được gọi là không gian cong dương. Ngoài ra, độ cong là đồng nhất và đẳng hướng. Nói chung, góc ở các đỉnh của tam giác cầu tuân theo quan hệ:

$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$

Ở đâu A là diện tích của tam giác và Rlà bán kính của mặt cầu. Hình ảnh sau đây mô tả một không gian cong tích cực.

Đối với một độ cong dương, các đường thẳng song song phải gặp nhau. Coi bề mặt trái đất là một không gian cong dương. Lấy hai điểm xuất phát trên đường xích đạo. Các đường cắt ngang đường xích đạo ở các góc vuông được gọi là các đường kinh độ. Vì những đường thẳng này cắt ngang đường xích đạo ở góc vuông, chúng có thể được gọi là những đường thẳng song song. Bắt đầu từ đường xích đạo, cuối cùng chúng giao nhau ở các cực. Phương pháp này đã được sử dụng bởiCarl Gauss và những người khác để hiểu cấu trúc liên kết của trái đất.

Xét một không gian cong âm (hình yên ngựa trong hình sau), tổng các góc trong của tam giác nhỏ hơn 180 ^o , tức là -

$$ \ alpha + \ beta + \ gamma <\ pi $$

Góc ở các đỉnh tuân theo quan hệ -

$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Độ cong bằng không

Một mặt phẳng có độ cong bằng không. Bây giờ đối với một không gian phẳng, nếu lấy một mặt phẳng và một hình tam giác được dựng bằng cách nối ba điểm với đường trắc địa (đường thẳng), thì tổng các góc bên trong sẽ là:

$$ \ alpha + \ beta + \ gamma = \ pi $$

Hình ảnh sau đây là một không gian 2 chiều phẳng.

Nếu người ta muốn một không gian là đồng nhất và đẳng hướng, thì chỉ còn lại ba khả năng: không gian có thể phẳng đồng nhất hoặc nó có thể có độ cong dương đều hoặc có thể có độ cong âm đồng nhất.

Hằng số độ cong có thể giả định bất kỳ giá trị nào trong ba giá trị sau.

$$ k = \ begin {case} +1, & for \: a \: positive \: curve \: space; \\\ quad 0, & for \: a \: flat \: space; \\ - 1, & for \: a \: negative \: Curve \: space; \ end {case} $$

Cấu trúc liên kết toàn cầu của vũ trụ

Vũ trụ có một cấu trúc liên kết nhất định, nhưng cục bộ nó có thể có các nếp nhăn. Tùy thuộc vào cách vật chất được phân bố trong không gian, có những biến thể nhỏ hơn về độ cong. Chúng ta hãy giả định rằng có một lớp vật thể có cùng kích thước thực bất kể nó ở đâu trong vũ trụ, có nghĩa là chúng giống như những ngọn nến tiêu chuẩn. Chúng không có cùng độ sáng, nhưng chúng có cùng kích thước.

Nếu vật thể ở trong không gian cong dương và các photon xuất phát từ điểm A (một đầu của vật thể) và B (đầu kia của vật thể), thì các photon sẽ truyền song song trong không gian cong dương qua đường trắc địa và cuối cùng chúng sẽ gặp nhau. . Đối với một người quan sát tại C, có vẻ như nó đến từ hai điểm khác nhau theo các hướng khác nhau.

Nếu vật thể ở trong vũ trụ cục bộ và chúng ta đo kích thước góc, nó không bị ảnh hưởng bởi độ cong. Nếu cùng một loại đối tượng được nhìn thấy ở độ lệch đỏ lớn hơn, thì kích thước góc không tương quan với.

$$ \ theta = \ frac {d} {r} $$

Ở đâu d là kích thước của đối tượng và rlà khoảng cách đến đối tượng, tức là nếu kích thước lớn hơn kích thước cục bộ, nghĩa là độ cong là dương. Hình ảnh sau đây là đại diện của photon được phát hiện trong một không gian cong dương.

Cần lưu ý rằng không có vật thể thiên văn thực sự nào có kích thước và hình thái tiêu chuẩn. Mặc dù cD hình elip khổng lồ - các thiên hà được cho là phù hợp với các ngọn nến tiêu chuẩn, nhưng chúng cũng được phát hiện là đang phát triển theo thời gian.

Tìm khoảng cách với các thiên hà

Trong phần này, chúng ta sẽ thảo luận về cách tìm khoảng cách đến một thiên hà bằng cách xem xét hình ảnh sau đây.

Hãy xem xét Dải Ngân hà tại (r, θ,) trong một khung nghỉ vũ trụ. Người ta có thể lấy = 0; (0, θ, ϕ), tức là trung tâm của vũ trụ bằng cách viện dẫn giả định về tính đồng nhất.

Hãy xem xét một thiên hà 'G' tại (r1, θ,). Khoảng cách (thích hợp) là khoảng cách xuyên tâm ngắn nhất mà một photon truyền được. Từ phép đối xứng không gian - thời gian, đường trắc địa rỗng từ r = 0 đến r = r1, có phương không đổi trong không gian. Trong sự truyền xuyên tâm của nó, toạ độ góc không thay đổi. Nếu tọa độ góc thay đổi, thì đó không phải là đường đi ngắn nhất. Đó là lý do tại sao thuật ngữ độ cong có mặt trong dr ² .

Những điểm cần nhớ

• Sự giãn nở của vũ trụ theo tất cả các hướng.

• Vũ trụ có thể tĩnh, giãn nở hoặc co lại tùy thuộc vào sự tiến hóa của yếu tố quy mô.

• Các thiên hà cD phát triển theo thời gian và do đó không thể được sử dụng làm nến tiêu chuẩn.

• Vũ trụ có cấu trúc liên kết nhất định, nhưng cục bộ nó có thể có các nếp nhăn.

Trong chương này, chúng ta sẽ thảo luận về Thông số Hubble cũng như Hệ số tỷ lệ.

• Prerequisite - Dịch chuyển đỏ vũ trụ, Nguyên lý vũ trụ.

• Assumption - Vũ trụ đồng nhất và đẳng hướng.

Hằng số của Hubble với Tỷ lệ Thay đổi Phân số của Hệ số Quy mô

Trong phần này, chúng ta sẽ liên hệ Hằng số của Hubble với tỷ lệ thay đổi của Hệ số quy mô theo phân số.

Chúng ta có thể viết vận tốc theo cách sau và đơn giản hóa.

$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$

$$ = \ frac {d [a (t) r_c} {dt} $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c) $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$

Đây, v là vận tốc lặn, a là hệ số quy mô và r_p là khoảng cách thích hợp giữa các thiên hà.

Hubble’s Empirical Formula thuộc về bản chất -

$$ v = H \ ast r_p $$

Do đó, so sánh hai phương trình trên, chúng ta thu được:

Hubble’s Parameter = Fractional rate of change of the scale factor

$$ H = da / dt \ ast 1 / a $$

Note- Đây không phải là một hằng số vì hệ số tỷ lệ là một hàm của thời gian. Do đó, nó được gọi là tham số của Hubble chứ không phải là hằng số của Hubble.

Theo kinh nghiệm, chúng tôi viết -

$$ H = V / D $$

Do đó, từ phương trình này, chúng ta có thể suy ra rằng vì D đang tăng lên và V là một hằng số, sau đó H giảm dần theo thời gian và sự giãn nở của vũ trụ.

Phương trình Friedmann trong Liên kết với Mô hình Robertson-Walker

Trong phần này, chúng ta sẽ hiểu cách sử dụng Phương trình Friedmann kết hợp với mô hình Robertson-Walker. Để hiểu điều này, chúng ta hãy lấy hình ảnh sau có khối lượng thử nghiệm ở khoảng cách xar_p từ khối lượng lớn M như một ví dụ.

Xem xét hình ảnh trên, chúng ta có thể biểu thị lực là -

$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$

Đây, G là hằng số hấp dẫn phổ quát và ρ là mật độ vật chất bên trong vũ trụ quan sát được.

Bây giờ, giả sử mật độ khối lượng đồng đều trong hình cầu, chúng ta có thể viết:

$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$

Sử dụng chúng trở lại trong phương trình lực, chúng ta nhận được -

$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$

Như vậy, ta có thể viết thế năng và động năng của khối lượng m như -

$$ V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$

$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$

Sử dụng Virial Theorem -

$$ U = KE + V $$

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Nhưng ở đây, $ r_p = ar_c $. Vì vậy, chúng tôi nhận được -

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Khi đơn giản hóa hơn nữa, chúng tôi thu được phương trình Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$

Đây Ulà một hằng số. Chúng ta cũng lưu ý rằng vũ trụ chúng ta đang sống hiện nay bị chi phối bởi vật chất, trong khi mật độ năng lượng bức xạ rất thấp.

Những điểm cần nhớ

• Thông số Hubble giảm dần theo thời gian và sự giãn nở của vũ trụ.

• Vũ trụ chúng ta đang sống hiện nay bị chi phối bởi vật chất và mật độ năng lượng bức xạ rất thấp.

Trong chương này, chúng ta sẽ hiểu Phương trình Friedmann là gì và nghiên cứu chi tiết về Mô hình Thế giới cho các hằng số độ cong khác nhau.

Phương trình Friedmann

Phương trình này cho chúng ta biết về sự giãn nở của không gian trong các mô hình đồng nhất và đẳng hướng của vũ trụ.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ $

Điều này đã được sửa đổi trong ngữ cảnh của General Relativity (GR) và Robertson-Walker Metric như sau.

Sử dụng phương trình GR -

$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$

Ở đâu klà hằng số độ cong. Vì thế,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} $ $

Ngoài ra, $ \ rho $ được thay thế bằng mật độ năng lượng bao gồm vật chất, bức xạ và bất kỳ dạng năng lượng nào khác. Nhưng đối với mục đích đại diện, nó được viết là $ \ rho $.

Các mô hình thế giới cho các hằng số độ cong khác nhau

Bây giờ chúng ta hãy xem xét các khả năng khác nhau tùy thuộc vào các giá trị hằng số độ cong.

Trường hợp 1: k = 1, hoặc Vũ trụ đóng

Đối với một vũ trụ đang giãn nở, $ da / dt> 0 $. Khi tiếp tục mở rộng, số hạng đầu tiên trong RHS của phương trình trên có dạng $ a ^ {- 3} $, trong khi số hạng thứ hai là $ a ^ {- 2} $. Khi hai số hạng trở nên bằng nhau, vũ trụ ngừng giãn nở. Sau đó -

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$

Ở đây, k = 1, do đó,

$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$

Một vũ trụ như vậy là hữu hạn và có thể tích hữu hạn. Đây được gọi là một Vũ trụ đóng.

Trường hợp 2: k = -1, hoặc Vũ trụ mở

Nếu k < 0, việc mở rộng sẽ không bao giờ dừng lại. Sau một số thời điểm, số hạng đầu tiên trên RHS có thể bị bỏ qua so với số hạng thứ hai.

Ở đây, k = -1. Do đó, $ da / dt ∼ c $.

Trong trường hợp này, vũ trụ đang quay cuồng. Một vũ trụ như vậy có không gian và thời gian vô hạn. Đây được gọi là một Vũ trụ Mở.

Trường hợp 3: k = 0, hoặc Vũ trụ phẳng

Trong trường hợp này, vũ trụ đang giãn nở với tốc độ giảm dần. Ở đây, k = 0. Do đó,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho $$

Một vũ trụ như vậy có không gian và thời gian vô hạn. Đây được gọi là một Vũ trụ phẳng.

Những điểm cần nhớ

• Phương trình Friedmann cho chúng ta biết về sự giãn nở của không gian trong các mô hình đồng nhất và đẳng hướng của vũ trụ.

• Tùy thuộc vào các giá trị hằng số độ cong khác nhau, chúng ta có thể có một Vũ trụ Đóng, Mở hoặc Phẳng.

Trong chương này, chúng ta sẽ thảo luận về Phương trình Chất lỏng và cách nó cho chúng ta biết về mật độ vũ trụ thay đổi theo thời gian.

Ước tính ρ _c và ρ trong Vũ trụ Hiện tại

Đối với vũ trụ hiện tại -

$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {- 3} \ simeq 10 \: hydro \: nguyên tử \: m ^ {- 3} $$

Có một loạt các mật độ tới hạn trong không gian bên ngoài của chúng ta. Giống như, đối với môi trường giữa các thiên hà $ \ rho_c $ là 1 nguyên tử hydro $ m ^ {- 3} $, trong khi đối với các đám mây phân tử thì nó là $ 10 ^ 6 $ nguyên tử hydro $ m ^ {- 3} $.

Chúng ta phải đo $ \ rho_c $ khi xem xét các mẫu không gian thích hợp. Trong thiên hà của chúng ta, giá trị của $ \ rho_c $ rất cao, nhưng thiên hà của chúng ta không phải là đại diện của toàn vũ trụ. Vì vậy, chúng ta nên đi ra ngoài không gian nơi nguyên lý vũ trụ học, tức là khoảng cách ≈ 300 Mpc. Nhìn vào 300 Mpc có nghĩa là nhìn ngược lại 1 tỷ năm, nhưng nó vẫn là vũ trụ hiện tại.

Các cuộc khảo sát như SDSS được tiến hành để xác định mật độ vật chất thực tế. Họ lấy một thể tích 5 × 500 × 5 Mpc ³ , đếm số lượng thiên hà và thêm tất cả ánh sáng đến từ các thiên hà này. Theo giả định rằng 1 L ≡ 1 M, tức là 1 Độ sáng mặt trời ≡ 1 Khối lượng mặt trời.

Chúng tôi thực hiện chuyển đổi ánh sáng sang khối lượng và sau đó chúng tôi cố gắng ước tính số lượng baryon dựa trên các hạt vật chất nhìn thấy có trong khối lượng đó.

Ví dụ,

$$ 1000L_ \ odot ≡ 1000M_ \ odot / m_p $$

Trong đó, m _p = khối lượng của proton.

Sau đó, chúng tôi nhận được gần đúng mật độ số baryon $ \ Omega b ∼ = 0,025 $. Điều này ngụ ý $ \ rho b = 0,25% $ của $ \ rho_c $. Các cuộc khảo sát khác nhau đã mang lại một giá trị hơi khác nhau. Vì vậy, trong vũ trụ cục bộ, mật độ vật chất nhìn thấy được ít hơn nhiều so với mật độ tới hạn, nghĩa là chúng ta đang sống trong một vũ trụ mở.

Khối lượng với hệ số 10 không được bao gồm trong các cuộc khảo sát này vì những cuộc khảo sát này có tính đến bức xạ điện từ chứ không phải vật chất tối. Đang cho, $ \ Omega_m = 0,3 - 0,4 $. Vẫn kết luận rằng chúng ta đang sống trong một vũ trụ mở.

Vật chất tối tương tác với lực hấp dẫn. Rất nhiều vật chất tối có thể ngăn cản quá trình mở rộng. Chúng tôi vẫn chưa chính thức hóa cách $ \ rho $ thay đổi theo thời gian, vì vậy chúng tôi cần một bộ phương trình khác.

Nhiệt động lực học nói rằng -

$$ dQ = dU + dW $$

Đối với một hệ thống đang phát triển về quy mô, $ dW = P dV $. Sự giãn nở của vũ trụ được mô hình là đoạn nhiệt tức là $ dQ = 0 $. Vì vậy, sự thay đổi thể tích sẽ xảy ra từ sự thay đổi của năng lượng bên trong dU.

Chúng ta hãy lấy một thể tích vũ trụ nhất định có bán kính đi lên đơn vị tức là $ r_c = 1 $. Nếu $ \ rho $ là mật độ của vật chất trong thể tích không gian này, thì

$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$

$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$

Ở đâu, Ulà mật độ Năng lượng. Hãy cùng chúng tôi tìm hiểu sự thay đổi của nội năng theo thời gian khi vũ trụ đang giãn nở.

$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$

Tương tự, sự thay đổi về âm lượng theo thời gian được đưa ra bởi,

$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

Thay $ dU = −P dV $. Chúng tôi nhận được,

$$ 4 \ pi a ^ 2 (c ^ 2 \ rho + P) \ dot {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$

$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Đây được gọi là Fluid Equation. Nó cho chúng ta biết mật độ của vũ trụ thay đổi như thế nào theo thời gian.

Áp suất giảm khi vũ trụ giãn nở. Tại mọi thời điểm áp suất thay đổi, nhưng không có sự chênh lệch áp suất giữa hai điểm trong thể tích đang xét, do đó, gradien áp suất bằng không. Chỉ vật liệu tương đối tính mới truyền áp suất, vật chất thì ít áp suất hơn.

Phương trình Friedmann cùng với Phương trình Chất lỏng mô hình vũ trụ.

Những điểm cần nhớ

• Vật chất tối tương tác với lực hấp dẫn. Rất nhiều vật chất tối có thể ngăn cản quá trình mở rộng.

• Phương trình Chất lỏng cho chúng ta biết mật độ của vũ trụ thay đổi như thế nào theo thời gian.

• Phương trình Friedmann cùng với Phương trình Chất lỏng mô hình vũ trụ.

• Chỉ vật liệu tương đối tính mới truyền áp suất, vật chất thì ít áp suất hơn.

Trong chương này, chúng ta sẽ thảo luận về các Giải pháp cho Phương trình Friedmann liên quan đến Vũ trụ Chi phối Vật chất. Trong vũ trụ học, bởi vì chúng ta đang nhìn thấy mọi thứ ở quy mô lớn, các hệ mặt trời, các thiên hà, mọi thứ xảy ra giống như các hạt bụi (đó là những gì chúng ta nhìn thấy bằng mắt), chúng ta có thể gọi nó là vũ trụ bụi hoặc vũ trụ chỉ vật chất.

bên trong Fluid Equation,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right) $$

Chúng ta có thể thấy có một điều khoản áp lực. Đối với một vũ trụ đầy bụi,P = 0, bởi vì mật độ năng lượng của vật chất sẽ lớn hơn áp suất bức xạ, và vật chất không chuyển động với tốc độ tương đối tính.

Vì vậy, Phương trình Chất lỏng sẽ trở thành,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho $$

$$ \ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$

$$ \ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0 $$

$$ \ Rightarrow \ rho a ^ 3 = \: hằng $$

$$ \ Rightarrow \ rho \ propto \ frac {1} {a ^ 3} $$

Không có trực giác ngược lại trong phương trình này vì mật độ phải chia tỷ lệ là $ a ^ {- 3} $ vì Khối lượng đang tăng là $ a ^ 3 $.

Từ mối quan hệ cuối cùng, chúng ta có thể nói rằng,

$$ \ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3 $$

Đối với vũ trụ hiện tại, a, bằng a₀ nên là 1. Vì vậy,

$$ \ rho (t) = \ frac {\ rho_0} {a ^ 3} $$

Trong một vũ trụ phẳng thống trị vật chất, k = 0. Vì vậy, phương trình Friedmann sẽ trở thành,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$

Bằng cách giải phương trình này, chúng ta sẽ nhận được,

$$ a \ propto t ^ {2/3} $$

$$ \ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Điều này có nghĩa là vũ trụ sẽ tiếp tục tăng với tốc độ giảm dần. Hình ảnh sau đây cho thấy sự mở rộng của một Vũ trụ Bụi.

Ρ Thay đổi theo thời gian như thế nào?

Hãy xem phương trình sau:

$$ \ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2 $$

Chúng tôi biết rằng hệ số tỷ lệ thay đổi theo thời gian là $ t ^ {2/3} $. Vì thế,

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Phân biệt nó, chúng ta sẽ nhận được,

$$ \ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right) $$

Chúng tôi biết rằng Hubble Constant Là,

$$ H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$

Đây là phương trình cho Einstein-de sitter Universe. Nếu chúng ta muốn tính tuổi hiện tại của vũ trụ thì,

$$ t_0 = t_ {age} = \ frac {2} {3H_0} $$

Sau khi đặt giá trị $ H_0 $ cho vũ trụ hiện tại, chúng ta sẽ nhận được giá trị tuổi của vũ trụ là 9 Gyrs. Có nhiềuGlobular Cluster trong thiên hà dải ngân hà của chúng ta có tuổi hơn thế.

Đó là tất cả về vũ trụ đầy bụi. Bây giờ, nếu bạn giả sử rằng vũ trụ bị chi phối bởi bức xạ chứ không phải bởi vật chất, thì mật độ năng lượng bức xạ sẽ là $ a ^ {- 4} $ chứ không phải là $ a ^ {- 3} $. Chúng ta sẽ xem thêm về nó trong chương tiếp theo.

Những điểm cần nhớ

• Trong vũ trụ học, mọi thứ xảy ra giống như các hạt bụi, do đó, chúng ta gọi nó là vũ trụ bụi hoặc vũ trụ chỉ vật chất.

• Nếu chúng ta giả định rằng vũ trụ bị chi phối bởi bức xạ chứ không phải bởi vật chất, thì mật độ năng lượng bức xạ là $ a ^ {- 4} $ chứ không phải là $ a ^ {- 3} $.

Trong chương này, chúng ta sẽ thảo luận về các Giải pháp cho Phương trình Friedmann liên quan đến Vũ trụ Chi phối Bức xạ. Lúc đầu, chúng ta so sánh mật độ năng lượng của vật chất với mật độ năng lượng của bức xạ. Điều này sẽ cho phép chúng ta biết được vũ trụ của chúng ta là vật chất chi phối hay bức xạ chi phối.

Mật độ năng lượng của bức xạ

Bức xạ phổ biến trong vũ trụ hiện nay có thể được cho là rất ít do các nguồn sao, mà chủ yếu là do CMB còn sót lại (Nền vi sóng vũ trụ).

Mật độ năng lượng của bức xạ, $ \ epsilon _ {\ gamma, 0} $, có thể được biểu thị như sau:

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$

Đây, a là hằng số bức xạ có biểu thức $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ bằng a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴. Nhiệt độ, T0, chúng ta xem xét ở đây, tương ứng với nhiệt độ của vật đen tương ứng với CMB.

Thay thế kết quả, chúng tôi có,

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} erg \: cm ^ {- 3} $$

Mật độ năng lượng của vật chất

Trong các phép tính sau, chúng ta có giả thiết làm việc với một vũ trụ phẳng và K = 0. Chúng ta coi mật độ năng lượng của vật chất là $ \ epsilon = \ rho c ^ 2 $. Chúng tôi xem xét những điều sau -

$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$

$$ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$

Như vậy, từ tính toán trên, chúng ta thấy rằng chúng ta đang sống trong một vũ trụ chi phối bởi vật chất. Điều này có thể được hỗ trợ bởi thực tế là CMB rất lạnh. Khi nhìn lại thời gian, chúng ta sẽ thấy nhiệt độ CMB trở nên nóng hơn, và có thể kết luận rằng có thể đã có một kỷ nguyên mà vũ trụ bị bức xạ chi phối.

Sự thay đổi của hệ số mật độ và tỷ lệ

Phương trình chất lỏng cho chúng ta thấy rằng -

$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Nếu chúng ta coi một vũ trụ đầy bụi, chúng ta sẽ có P = 0. Bỏ qua các kết quả trước đó, chúng ta coi vũ trụ như bị chi phối bởi bức xạ.

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$

Sử dụng quan hệ áp suất của $ P_ {rad} = \ rho c ^ {2/3} $ ta có -

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$

$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$

Khi đơn giản hóa hơn nữa, chúng tôi có,

$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$

$$ \ rho_ {rad} a ^ 4 = \: hằng $$

$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$

Kết quả chương trình trên một nghịch đảo 4 ^thứ biến sức mạnh của một bằng $ \ rho $.

Điều này có thể được hiểu về mặt vật lý là $ a ^ {- 3} $ đến từ sự thay đổi về khối lượng khi nó tăng lên. $ A ^ {- 1} $ còn lại có thể được coi là năng lượng mà photon bị mất đi do sự giãn nở của không gian trong vũ trụ (Dịch chuyển đỏ vũ trụ 1 + z = a ^-1 ).

Hình ảnh sau đây cho thấy sự biến thiên của vật chất và mật độ bức xạ theo thời gian.

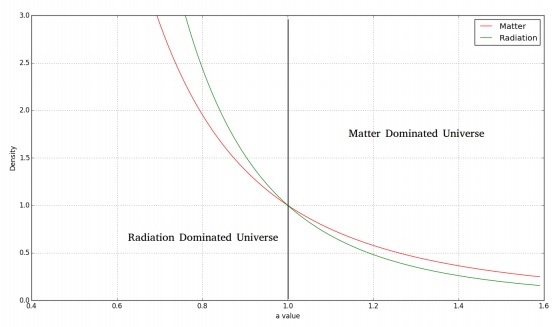
Đối với một vũ trụ phẳng, bức xạ chiếm ưu thế, chúng ta sẽ có phương trình Friedmann như sau:

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$

Khi đơn giản hóa và áp dụng giải pháp cho phương trình vi phân, chúng ta có -

$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$

$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$

Do đó, chúng ta có -

$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$

Từ phương trình trên, chúng ta thấy rằng tốc độ tăng của hệ số tỷ lệ nhỏ hơn tốc độ gia tăng của vũ trụ bụi.

Những điểm cần nhớ

• Bức xạ phổ biến trong vũ trụ hiện nay có thể được cho là rất ít từ các nguồn sao.

• Đối với một vũ trụ đầy bụi, áp suất bằng không.

• CMB rất lạnh lùng.

Khu vực Năng lượng Tối là một khu vực rất xám trong thiên văn học vì nó là một tham số tự do trong tất cả các phương trình, nhưng không có ý tưởng rõ ràng đây chính xác là gì.

Chúng ta sẽ bắt đầu với các phương trình Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} $$

Hầu hết các cuốn sách cơ bản về vũ trụ học, chúng đều bắt đầu bằng việc mô tả năng lượng tối từ tập này mà trước khi có sự quan sát của Hubble, vũ trụ đóng và tĩnh.

Bây giờ, để vũ trụ là tĩnh ở phía bên phải, cả hai số hạng phải khớp và chúng phải bằng 0, nhưng nếu số hạng đầu tiên lớn hơn số hạng thứ hai, thì vũ trụ sẽ không tĩnh, vì vậy Einstein đã bỏ tham số tự do. ∧ vào phương trình trường để làm cho vũ trụ tĩnh, vì vậy ông lập luận rằng bất kể số hạng đầu tiên là gì so với số hạng thứ hai, bạn luôn có thể nhận được một vũ trụ tĩnh nếu có thêm một thành phần trong phương trình, có thể bù đắp sai lệch phù hợp giữa hai thuật ngữ này.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

$$ \ left (\ frac {\ ddot {a}} {a} \ right) = - \ frac {4 \ pi G} {3} \ left (\ rho + \ frac {3P} {c ^ 2} \ phải) + \ frac {\ wedge} {3} $$

Trong đó $ P = \ rho \ ast c ^ 2/3 $ và $ \ wedge = \ rho \ ast c ^ 2 $ là Tham số vũ trụ. (Dấu hiệu tiêu cực là chỉ vì sự hấp dẫn)

Trong phương trình trên (phương trình gia tốc) -

• $ 3P / c ^ 2 $ là áp suất âm do bức xạ,

• $ -4 \ pi G / 3 $ là lực hút do trọng lực, và

• $ \ wedge / 3 $ đóng góp tích cực.

Số hạng thứ ba đóng vai trò là lực đẩy vì một phần khác của phương trình là lực hút.

Ý nghĩa vật lý của phương trình là ˙a = 0bởi vì không có bất kỳ bằng chứng nào cho thấy vũ trụ đang giãn nở. Điều gì sẽ xảy ra nếu hai thuật ngữ này không khớp với nhau, vì vậy tốt hơn là thêm một thành phần và tùy thuộc vào phần bù mà chúng ta luôn có thể thay đổi giá trị của tham số tự do.

Vào thời điểm đó, không có lời giải thích vật lý nào về các thông số vũ trụ này, đó là lý do tại sao khi giải thích về vũ trụ giãn nở được phát hiện vào những năm 1920, nơi Einstein ngay lập tức phải ném hằng số này ra ngoài.

Giải thích về điều này cosmological constant vẫn được sử dụng vì nó giải thích một phiên bản khác của vũ trụ, nhưng định nghĩa về hằng số vũ trụ này, cách giải thích liên tục thay đổi theo thời gian.

Bây giờ khái niệm về hằng số vũ trụ này đã được đưa trở lại vũ trụ học vì nhiều lý do. Một trong những lý do là chúng ta quan sát được mật độ năng lượng của các thành phần khác nhau của vũ trụ (baryonic, vật chất tối, bức xạ), vì vậy chúng ta biết rằng thông số này là gì. Các quan sát độc lập sử dụngcosmic microwave background cho thấy rằng k = 0.

$$ CMB, k = 0 \: \ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \ khoảng 10 \: Hydro \: nguyên tử.m ^ {- 3} $$

Đối với k là 0, $ \ rho $ phải bằng $ \ rho_c $, nhưng mọi thứ chúng ta biết nếu chúng ta cộng nó lên mà không cho 0, có nghĩa là có một số thành phần khác cho thấy rằng nó nhỏ hơn nhiều $ \ rho_c $.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$

Thêm một bằng chứng về năng lượng tối đến từ Type 1 Supernova Observationxảy ra khi sao lùn trắng tích tụ vật chất và vượt quá giới hạn Chandrashekhar, một giới hạn rất chính xác (≈ 1,4M). Bây giờ mỗi khi Vụ nổ Siêu tân tinh Loại 1 xảy ra, chúng ta có cùng khối lượng, nghĩa là tổng năng lượng liên kết của hệ là như nhau và lượng năng lượng ánh sáng mà chúng ta có thể nhìn thấy là như nhau.

Tất nhiên, ánh sáng của siêu tân tinh sẽ tăng lên và sau đó mờ đi, nhưng nếu bạn đo độ sáng cực đại thì nó sẽ luôn giống nhau khiến nó trở thành một ứng cử viên tiêu chuẩn. Vì vậy, với Siêu tân tinh Loại 1, chúng tôi đã sử dụng để đo thành phần sinh học của vũ trụ và các nhà thiên văn học phát hiện ra rằng siêu tân tinh có độ dịch chuyển đỏ cao mờ hơn 30% - 40% so với siêu tân tinh có độ dịch chuyển đỏ thấp và có thể giải thích được nếu có -số không∧ kỳ hạn.

Trong các mô hình vũ trụ DE (Dark Energy)được coi như một chất lỏng, có nghĩa là chúng ta có thể viết phương trình trạng thái cho nó. Phương trình trạng thái là phương trình kết nối các biến như Áp suất, Mật độ, Nhiệt độ và Thể tích của hai trạng thái khác nhau của vật chất.

Theo chiều hướng chúng ta thấy,

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$

Mật độ năng lượng của DE,

$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$

Tham số mật độ năng lượng tối,

$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$

$ \ Omega_ \ wedge $ là mật độ của năng lượng tối theo mật độ tới hạn.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$

Có một số giả thuyết về năng lượng tối, nó đang đẩy lùi vũ trụ và khiến vũ trụ giãn nở. Một giả thuyết cho rằng năng lượng tối này có thể là mật độ năng lượng chân không. Giả sử bản thân không gian đang xử lý một số năng lượng và khi bạn đếm lượng vật chất baryonic, vật chất tối và bức xạ trong một đơn vị thể tích không gian, bạn cũng đang đếm lượng năng lượng liên kết với không gian, nhưng nó không rõ ràng. rằng năng lượng tối thực sự là một mật độ năng lượng chân không.

Chúng ta biết rằng mối quan hệ giữa mật độ và hệ số tỷ lệ đối với vật chất tối và bức xạ là,

$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$

$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$

Chúng ta có biểu đồ hệ số tỷ lệ mật độ v / s. Trong cùng một biểu đồ, chúng ta có thể thấy rằng $ \ rho_ \ wedge $ là một hằng số với sự giãn nở của vũ trụ mà không phụ thuộc vào hệ số tỷ lệ.

Hình ảnh sau đây cho thấy mối quan hệ giữa mật độ và hệ số tỷ lệ.

‘ρ’ v/s ‘a’(hệ số tỷ lệ liên quan đến thời gian) trong cùng một đồ thị, năng lượng tối được mô hình hóa như một hằng số. Vì vậy, bất kỳ năng lượng tối nào chúng ta đo được trong vũ trụ hiện tại, nó đều là một hằng số.

Những điểm cần nhớ

• Các quan sát độc lập sử dụng nền vi sóng vũ trụ cho thấy k = 0.

• $ \ rho_ \ wedge $ là một hằng số với sự giãn nở của vũ trụ không phụ thuộc vào hệ số tỷ lệ.

• Lực hấp dẫn cũng thay đổi theo thời gian được gọi là modified Newtonian dynamics.

Trong chương này, chúng ta sẽ thảo luận về các Đường cong Xoay Thiên hà Xoắn ốc và bằng chứng về Vật chất Tối.

Vật chất tối và sự thật quan sát về Vật chất tối

• Bằng chứng ban đầu về vật chất tối là study of the Kinematics of Spiral Galaxy.

• Mặt trời cách tâm Thiên hà của chúng ta 30.000 ánh sáng. Vận tốc tâm thiên hà là 220 km / s.

• Tại sao vận tốc lại là 220 km / s mà không phải là 100 km / s hay 500 km / s? Cái gì chi phối chuyển động tròn đều của vật?

• Khối lượng nằm trong bán kính giúp phát hiện vận tốc trong Vũ trụ.

Sự quay của Dải Ngân hà hoặc Thiên hà Xoắn ốc - Sự quay Vi sai

• Angular Velocity thay đổi theo khoảng cách từ trung tâm.

• Khoảng thời gian quỹ đạo phụ thuộc vào khoảng cách từ tâm.

• Vật chất ở gần trung tâm Thiên hà có khoảng thời gian ngắn hơn và vật chất ở xa Trung tâm thiên hà có khoảng thời gian lớn hơn.

Đường cong xoay

• Dự đoán sự thay đổi vận tốc với Galactic centric radius. Đường cong cho vận tốc thay đổi theo bán kính quỹ đạo.

• Khi chúng ta nhìn thấy mọi thứ chuyển động, chúng ta nghĩ rằng chính lực hấp dẫn ảnh hưởng đến chuyển động quay.

• Sự phân bố khối lượng thay đổi theo bán kính. Mật độ vật chất sẽ dự đoán đường cong xoay. Đường cong quay dựa trên mật độ vật chất, thay đổi theo bán kính.

Độ sáng bề mặt

• Chúng tôi chọn miếng dán và xem lượng ánh sáng phát ra.

• Lượng ánh sáng phát ra từ miếng dán được gọi là Độ sáng bề mặt.

• Đơn vị của nó là mag/arcsec².

• Nếu chúng ta thấy độ sáng bề mặt thay đổi theo bán kính, chúng ta có thể thấy chất sáng thay đổi theo bán kính.

  $$ \ mu (r) \ propto exp \ left (\ frac {-r} {h_R} \ right) $$

  $ h_R $ là độ dài tỷ lệ. $ \ mu (r) = \ mu_o \ ast exp \ left (\ frac {-r} {h_R} \ right) $

• $ h_R $ là gần 3 kpc đối với Milky way.

Thiên hà Xoắn ốc

Để các Nhà thiên văn hiểu được đường cong quay, họ chia các Thiên hà thành hai thành phần, đó là -

• Disk
• Bulge

Hình sau cho thấy một khối lồi cầu Trung tâm + Đĩa tròn. Sự phân bố sao và khí khác nhau ở chỗ phồng và đĩa.

Chuyển động học của các Thiên hà Xoắn ốc

• Vận tốc tròn của vật bất kỳ - Đối với vật phồng là (r <Rb).

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

  $$ M (r) = \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$

• Đối với đĩa - (Rb <r <Rd)

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

• Bulge có mật độ sao gần như không đổi.

• Mật độ bên trong phần phình ra là không đổi (không thay đổi theo khoảng cách bên trong phần phình ra).

• Trong một đĩa, mật độ sao giảm theo bán kính. Bán kính tăng thì chất phát sáng giảm.

• Hàng loạt - $ V (r) \ propto r $

• Trong đĩa - $ V (r) \ propto 1 / \ sqrt {r} $

Đường cong quay của các thiên hà xoắn ốc

• Thông qua Spectroscopy (các thiên hà lân cận - thiên hà phân giải theo không gian), chúng tôi tạo ra đường cong quay.

• Như đã đề cập ở trên, chúng ta thấy rằng đường cong quay phẳng ở các vùng bên ngoài, tức là các vật chuyển động nhanh ở các vùng bên ngoài, thường không được mong đợi ở dạng này.

• Tốc độ quỹ đạo tăng khi bán kính của vùng bên trong tăng lên, nhưng nó sẽ phẳng ở vùng bên ngoài.

Vật chất tối

Vật chất tối được cho là Thành phần không phát sáng của Vũ trụ. Hãy để chúng tôi hiểu về vật chất tối thông qua các gợi ý sau.

• Các đường cong quay phẳng phản ánh những gì chúng ta thấy về sự phân bố của các ngôi sao và khí trong các thiên hà xoắn ốc.

• Độ sáng bề mặt của đĩa giảm dần theo cấp số nhân với bán kính, ngụ ý rằng khối lượng vật chất phát sáng, chủ yếu là các ngôi sao, tập trung xung quanh trung tâm thiên hà.

• Việc làm phẳng đường cong quay gợi ý rằng tổng khối lượng của thiên hà trong bán kính nào đó r luôn luôn tăng với sự gia tăng trong r.

• Điều này chỉ có thể được giải thích nếu có một lượng lớn khối lượng hấp dẫn vô hình trong các thiên hà này không phát ra bức xạ điện từ.

• Các phép đo đường cong quay của các thiên hà xoắn ốc là một trong những bằng chứng thuyết phục nhất về vật chất tối.

Bằng chứng về Vật chất tối

• Thiếu khối lượng - gấp 10 lần khối lượng phát sáng.

• Phần lớn vật chất tối này phải nằm trong vầng hào quang của thiên hà: Một lượng lớn vật chất tối trong đĩa có thể làm xáo trộn sự ổn định lâu dài của đĩa trước các lực thủy triều.

• Một số phần nhỏ của vật chất tối trong đĩa có thể là baryonic - sao mờ (sao lùn nâu, sao lùn đen), và tàn dư sao nhỏ gọn (sao neutron, lỗ đen). Nhưng vật chất tối baryonic như vậy không thể giải thích được quy mô đầy đủ của khối lượng bị thiếu trong các thiên hà.

• Cấu hình mật độ của Vật chất tối - $ M (r) \ propto r $ và $ \ rho (r) \ propto r ^ {- 2} $.

• Dữ liệu về đường cong quay của các thiên hà xoắn ốc phù hợp với vật chất tối phân bố trong vầng hào quang của chúng.

• Quầng tối này tạo nên phần lớn tổng khối lượng của thiên hà.

• Tất cả các vật chất baryonic (sao, cụm sao, ISM, v.v.) được giữ lại với nhau bằng thế năng hấp dẫn của quầng vật chất tối này.

Phần kết luận

• Vật chất tối chỉ được phát hiện thông qua tương tác hấp dẫn của chúng với một vật chất thông thường. Chưa quan sát thấy tương tác với ánh sáng (không có lực điện từ).

• Neutrinos- Tích điện ít hơn, tương tác yếu, nhưng khối lượng quá nhỏ (<0,23 eV). Hạt DM phải có E> 10 eV hoặc hơn để giải thích sự hình thành cấu trúc.

• Các hạt khối lượng lớn tương tác yếu (WIMPS) có thể là nguồn gốc của Vật chất tối.

Những điểm cần nhớ

• Vật chất gần trung tâm Thiên hà có khoảng thời gian ngắn hơn.

• Bulge có mật độ sao gần như không đổi.

• Độ sáng bề mặt của đĩa giảm dần theo cấp số nhân với bán kính.

• Một lượng lớn vật chất tối trong đĩa có thể làm xáo trộn sự ổn định lâu dài của đĩa trước các lực thủy triều.

Bằng chứng trực tiếp đầu tiên về vật chất tối đến từ Frids Ricky. Ông đã thực hiện một số quan sát lần đầu tiên tiết lộ vật chất tối. Những quan sát của ông đã xem xét chuyển động tổng thể bên trong cụm thiên hà.

Các đối tượng mở rộng là các cụm thiên hà và chúng được coi là cấu trúc liên kết. Những thiên hà này đang chuyển động đối với trung tâm cụm nhưng không bay đi. Chúng tôi nhìn vào chuyển động tổng thể của thiên hà.

Giả định: Tốc độ đại diện cho tiềm năng cơ bản

Mỗi thiên hà sẽ có chuyển động thích hợp riêng của nó trong cụm và Hubble Flow Component. Các thiên hà nhỏ hơn thì nhỏ hơn, phần lớn ánh sáng đến từ M31 và MW, có một số thiên hà lùn. Đối với phân tích thô của chúng tôi, chúng tôi chỉ có thể sử dụng M31 và MW và đánh giá khối lượng động của nhóm cục bộ.

Giữa ta và M31 có một vận tốc tương đối. Nó là thô, nhưng nó là sự thật. Câu chuyện bắt đầu từ rất lâu khi M31 và MW ở gần nhau, vì họ là thành viên của một cụm mà họ di chuyển ra xa nhau. Sau một thời gian, họ đạt đến sự tách biệt tối đa, sau đó đến gần nhau hơn.

Giả sử rằng khoảng cách tối đa có thể đạt tới là $ r_ {max} $. Bây giờ họ có một sự tách biệt được gọi làr. Để choMlà khối lượng kết hợp của MW và M31. Chúng tôi không biết khi nào đạt đến $ r_ {max} $.

$$ \ frac {GM} {r_ {max}} = \: Tiềm năng \: tại \: r_ {max} $$

Khi những thiên hà này đến gần nhau tại một thời điểm r nào đó, thì năng lượng của hệ sẽ là:

$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$

σ là vận tốc tương đối của cả hai thiên hà. M chỉ là khối lượng giảm, nhưng khối lượng thử nghiệm là 1. σ là vận tốc của bất kỳ vật thể nào ở khoảng cách rtừ trung tâm của cụm. Chúng tôi tin rằng cụm này nằm trong phương trình động vì định lý virial là đúng. Vì vậy, các thiên hà không thể đến với vận tốc khác nhau.

Những thiên hà này sẽ mất bao nhiêu thời gian để đạt được khoảng cách tối đa?

Để hiểu điều này, chúng ta hãy xem xét phương trình sau đây.

$$ \ frac {1} {2} \ left (\ frac {dr} {dt} \ right) ^ 2 = \ frac {GM} {r} - \ frac {GM} {r_ {max}} $$

$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left (\ frac {1} {r} - \ frac {1} {r_ {max}} \ right) ^ 2 $$

$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$

Trong đó, M = khối lượng động lực của nhóm cục bộ. Tổng thời gian từ khi bắt đầu cho đến khi kết thúc va chạm là $ 2t_ {max} $. Vì thế,

$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$

Và $ t_0 $ là tuổi hiện tại của vũ trụ.

Nếu $ t_ {max} thực tế <RHS $, thì chúng tôi có giới hạn thấp hơn cho thời gian. $ D / \ sigma $ là thời gian chúng lại va chạm. Ở đây, chúng tôi đã giả định σ là hằng số.

$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$

$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$

Ở đây, σ = vận tốc tương đối giữa MW và M31.

$$ M_ {dynamic} = 3 \ times 10 ^ {12} M_0 $$

$$ M_ {MW} ^ {lum} = 3 \ lần 10 ^ {10} M_0 $$

$$ M_ {M31} ^ {lum} = 3 \ lần 10 ^ {10} M_0 $$

Nhưng trên thực tế, khối lượng động được tìm thấy khi xem xét mọi thiên hà trong cụm. Khối lượng bị thiếu là vật chất tối vàFrids Rickynhận thấy rằng các thiên hà trong cụm hôn mê đang di chuyển quá nhanh. Ông dự đoán sự tồn tại của sao neutron vào năm sau khi sao neutron được phát hiện và sử dụng kính thiên văn Palomar để tìm siêu tân tinh.

Những điểm cần nhớ

• Bằng chứng trực tiếp đầu tiên về vật chất tối đến từ Frids Ricky.

• Các đối tượng mở rộng là các cụm thiên hà và chúng được coi là bound structures.

• Dynamic mass được tìm ra khi xem xét mọi thiên hà trong cụm.

Trong chương này, chúng ta sẽ thảo luận về các tham số Mật độ và Hubble.

Tham số Hubble

Tham số Hubble được xác định như sau:

$$ H (t) \ equiv \ frac {da / dt} {a} $$

đo lường mức độ thay đổi nhanh chóng của hệ số quy mô. Nói một cách tổng quát hơn, sự phát triển của hệ số tỷ lệ được xác định bởi Phương trình Friedmann.

$$ H ^ 2 (t) \ equiv \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

Ở đâu, ∧ là một hằng số vũ trụ.

Đối với một vũ trụ phẳng, k = 0, do đó Phương trình Friedmann trở thành -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$

Đối với một vũ trụ chi phối vật chất, mật độ thay đổi như sau:

$$ \ frac {\ rho_m} {\ rho_ {m, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 3 \ Rightarrow \ rho_m = \ rho_ {m, 0} a ^ {- 3} $$

và, đối với một vũ trụ chi phối bức xạ, mật độ thay đổi như sau:

$$ \ frac {\ rho_ {rad}} {\ rho_ {rad, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad, 0} a ^ {- 4} $$

Hiện tại, chúng ta đang sống trong một vũ trụ chi phối vật chất. Do đó, xem xét $ \ rho ≡ \ rho_m $, chúng tôi nhận được -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {\ wedge} {3} $$

Hằng số vũ trụ và mật độ năng lượng tối có mối quan hệ như sau:

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$

Từ điều này, chúng tôi nhận được -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$

Ngoài ra, mật độ tới hạn và hằng số Hubble có liên quan như sau:

$$ \ rho_ {c, 0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Rightarrow \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} $$

Từ điều này, chúng tôi nhận được -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ {m, 0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ \ wedge $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 3} + H_0 ^ 2 \ Omega _ {\ wedge, 0 } $$

$$ (\ dot {a}) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 1} + H_0 ^ 2 \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} \ frac {1} {a} + \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) + \ Omega _ {\ wedge, 0} \ frac {1} { (1 + z) ^ 2} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 (1 + z) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge , 0} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {\ wedge, 0} $$

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge, 0} $$

Ở đây, $ H (z) $ là tham số Hubble phụ thuộc vào dịch chuyển màu đỏ. Điều này có thể được sửa đổi để bao gồm tham số mật độ bức xạ $ \ Omega_ {rad} $ và tham số mật độ độ cong $ \ Omega_k $. Phương trình đã sửa đổi là -

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4+ \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

$$ Hoặc, \: \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = E (z) $$

$$ Hoặc, \: H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Ở đâu,

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Điều này cho thấy thông số Hubble thay đổi theo thời gian.

Cho Einstein-de Sitter Vũ trụ, $ \ Omega_m = 1, \ Omega_ \ wedge = 0, k = 0 $.

Đưa những giá trị này vào, chúng tôi nhận được -

$$ H (z) = H_0 (1 + z) ^ {\ frac {3} {2}} $$

cho thấy sự tiến hóa theo thời gian của tham số Hubble cho vũ trụ Einstein-de Sitter.

Tham số mật độ

Tham số mật độ, $ \ Omega $, được định nghĩa là tỷ số giữa mật độ thực tế (hoặc quan sát được) ρ với mật độ tới hạn $ \ rho_c $. Đối với bất kỳ số lượng nào $ x $ tham số mật độ tương ứng, $ \ Omega_x $ có thể được biểu diễn toán học dưới dạng:

$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$

Đối với các đại lượng khác nhau đang được xem xét, chúng ta có thể xác định các thông số mật độ sau.

Không.	Định lượng	Tham số mật độ
1	Baryons	$ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $
2	Vật chất (Baryonic + Dark)	$ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $
3	Năng lượng tối	$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $
4	Sự bức xạ	$ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $

Nơi mà các biểu tượng có ý nghĩa thông thường của chúng.

Những điểm cần nhớ

• Sự phát triển của hệ số tỷ lệ được xác định bởi Friedmann Equation.

• H(z) là thông số Hubble phụ thuộc dịch chuyển màu đỏ.

• Các Hubble Parameter thay đổi theo thời gian.

• Các Density Parameter được định nghĩa là tỷ số giữa mật độ thực tế (hoặc quan sát được) với mật độ tới hạn.

Như đã thảo luận trong các chương trước, sự phát triển theo thời gian của thông số Hubble được đưa ra bởi:

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Ở đâu z là sự thay đổi màu đỏ và E(Z) là -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega ^ {\ wedge, 0} $$

Nếu sự giãn nở của vũ trụ là không đổi, thì tuổi thực của vũ trụ được đưa ra như sau:

$$ t_H = \ frac {1} {H_0} $$

Nếu nó là vũ trụ chi phối vật chất, tức là vũ trụ Einstein Desitter, thì tuổi thực của vũ trụ được cho bởi -

$$ t_H = \ frac {2} {3H_0} $$

Quy mô và Dịch chuyển đỏ được xác định bởi -

$$ a = \ frac {a_0} {1 + z} $$

Tuổi của vũ trụ theo tham số vũ trụ được suy ra như sau.

Thông số Hubble được cung cấp bởi -

$$ H = \ frac {\ frac {da} {dt}} {a} $$

Phân biệt, chúng tôi nhận được -

$$ da = \ frac {-dz} {(1 + z) ^ 2} $$

Ở đâu a₀ = 1 (giá trị hiện tại của hệ số tỷ lệ)

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z) ^ 2} $$

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$

$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$

$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

$$ dt = \ frac {-dz} {H_0E (z) ^ {\ frac {1} {2}} (1 + z)} $$

Nếu chúng ta muốn tìm tuổi của vũ trụ tại bất kỳ dịch chuyển đỏ nhất định nào ‘z’ sau đó -

$$ t (z) = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac {1} {2}} (1+ z)} dz $$

Ở đâu k là tham số mật độ độ cong và -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Để tính tuổi hiện tại của vũ trụ, hãy lấy z₁ = 0.

$$ t (z = 0) = t_ {age} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac { 1} {2}} (1 + z)} dz $$

Đối với Mô hình Desitter Einstein, tức là, $ \ Omega_m = 1 $, $ \ Omega_ {rad} = 0 $, $ \ Omega_k = 0 $, $ \ Omega_ \ wedge = 0 $, phương trình cho tuổi của vũ trụ trở thành -

$$ t_ {age} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z) ^ {\ frac {5} {2}}} dz $ $

Sau khi giải tích phân, chúng ta nhận được -

$$ t_H = \ frac {2} {3H_0} $$

Bầu trời đêm giống như một Cosmic Time Machine.Bất cứ khi nào chúng ta quan sát một hành tinh, ngôi sao hoặc thiên hà xa xôi, chúng ta đang nhìn thấy nó như cách đây hàng giờ, hàng thế kỷ hoặc thậm chí hàng thiên niên kỷ. Điều này là do ánh sáng truyền đi với một tốc độ hữu hạn (tốc độ ánh sáng) và với khoảng cách lớn trong Vũ trụ, chúng ta không nhìn thấy các vật thể như bây giờ, mà như khi ánh sáng được phát ra. Khoảng thời gian trôi qua giữa - khi chúng ta phát hiện ra ánh sáng ở đây trên Trái đất và khi nó được phát ra từ nguồn ban đầu, được gọi làLookback Time (t_L(z₁)).

Vì vậy, thời gian xem lại được đưa ra bởi -

$$ t_1 (z_1) = t_0-t (z_1) $$

Thời gian nhìn lại của Vũ trụ Desitter Einstein là -

$$ t_L (z) = \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z) ^ {\ frac {3} {2}}} \ right] $$

Những điểm cần nhớ

• Bất cứ khi nào chúng ta quan sát một hành tinh, ngôi sao hoặc thiên hà xa xôi, chúng ta đang nhìn thấy nó như cách đây hàng giờ, hàng thế kỷ hoặc thậm chí hàng thiên niên kỷ.

• Khoảng thời gian trôi qua giữa - khi chúng ta phát hiện ra ánh sáng ở đây trên Trái đất và khi nó được phát ra từ nguồn ban đầu, được gọi là thời gian nhìn lại.

Trong chương này, chúng ta sẽ hiểu Khoảng cách Đường kính Góc là gì và nó giúp ích như thế nào trong Vũ trụ học.

Đối với vũ trụ hiện tại -

• $ \ Omega_ {m, 0} \: = \: 0,3 $

• $ \ Omega _ {\ wedge, 0} \: = \: 0,69 $

• $ \ Omega_ {rad, 0} \: = \: 0,01 $

• $ \ Omega_ {k, 0} \: = \: 0 $

Chúng tôi đã nghiên cứu hai loại khoảng cách cho đến nay -

• Proper distance (lp) - Khoảng cách mà các photon truyền từ nguồn đến chúng ta, tức là Instantaneous distance.

• Comoving distance (lc) - Khoảng cách giữa các đối tượng trong một không gian không mở rộng, tức là distance in a comoving frame of reference.

Khoảng cách như một chức năng của Dịch chuyển đỏ

Hãy xem xét một thiên hà phát ra một photon tại một thời điểm t₁ được phát hiện bởi người quan sát tại t₀. Chúng ta có thể viết khoảng cách thích hợp đến thiên hà là -

$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$

Hãy để dịch chuyển đỏ của thiên hà là z,

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ phân số {1} {a} $$

$$ \ do đó \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$

Bây giờ, khoảng cách di chuyển của thiên hà bất cứ lúc nào t sẽ là -

$$ l_c = \ frac {l_p} {a (t)} $$

$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$

Về mặt z,

$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$

Có hai cách để tìm khoảng cách, như sau:

Mối quan hệ Flux-Luminosity

$$ F = \ frac {L} {4 \ pi d ^ 2} $$

Ở đâu d là khoảng cách tại nguồn.

Khoảng cách đường kính góc của nguồn

Nếu chúng ta biết kích thước của một nguồn, chiều rộng góc của nó sẽ cho chúng ta biết khoảng cách của nó với người quan sát.

$$ \ theta = \ frac {D} {l} $$

Ở đâu l là khoảng cách đường kính góc của nguồn.

• θ là kích thước góc của nguồn.

• D là kích thước của nguồn.

Hãy xem xét một thiên hà có kích thước D và kích thước góc dθ.

Chúng ta biết rằng,

$$ d \ theta = \ frac {D} {d_A} $$

$$ \ do đó D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ bởi vì dr ^ 2 = 0; \: d \ phi ^ 2 \ khoảng 0 $$

$$ \ Rightarrow D = a (t) rd \ theta $$

Thay đổi r đến r_c, khoảng cách sắp đi của thiên hà, chúng ta có -

$$ d \ theta = \ frac {D} {r_ca (t)} $$

Đây, nếu chúng ta chọn t = t₀, chúng tôi kết thúc việc đo khoảng cách hiện tại đến thiên hà. NhưngDđược đo tại thời điểm phát ra photon. Do đó, bằng cách sử dụngt = t₀, chúng ta nhận được khoảng cách lớn hơn tới thiên hà và do đó đánh giá thấp kích thước của nó. Do đó, chúng ta nên sử dụng thời giant₁.

$$ \ do đó d \ theta = \ frac {D} {r_ca (t_1)} $$

So sánh điều này với kết quả trước đó, chúng tôi nhận được -

$$ d_ \ wedge = a (t_1) r_c $$

$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ bởi vì 1 + z_1 = \ frac {1} {a (t_1)} $$

Vì thế,

$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$

d_A là Khoảng cách Đường kính Góc cho đối tượng.

Những điểm cần nhớ

• Nếu chúng ta biết kích thước của một nguồn, chiều rộng góc của nó sẽ cho chúng ta biết khoảng cách của nó với người quan sát.

• Khoảng cách thích hợp là khoảng cách mà các photon truyền từ nguồn đến chúng ta.

• Khoảng cách di chuyển là khoảng cách giữa các đối tượng trong một không gian không mở rộng.

Như đã thảo luận trong chương trước, khoảng cách đường kính góc tới nguồn tại dịch chuyển màu đỏ z được đưa ra bởi -

$$ d_ \ wedge (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $ $

$$ d_ \ wedge (z_ {gal}) = \ frac {r_c} {1 + z_ {gal}} $$

trong đó $ r_c $ là khoảng cách sắp kết thúc.

Khoảng cách độ sáng phụ thuộc vào vũ trụ học và nó được định nghĩa là khoảng cách mà thông lượng quan sát được f là từ một đối tượng.

Nếu đã biết độ sáng nội tại $ d_L $ của một vật thể ở xa, chúng ta có thể tính độ sáng của nó bằng cách đo từ thông $ f $ được xác định bởi -

$$ d_L (z) = \ sqrt {\ frac {L} {4 \ pi f}} $$

Năng lượng Photon chuyển sang màu đỏ.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$

trong đó $ \ lambda_ {obs}, \ lambda_ {emi} $ được quan sát và phát ra độ dài sóng và $ a_0, a_e $ là các hệ số tỷ lệ tương ứng.

$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$

trong đó $ \ Delta_t {obs} $ được quan sát là khoảng thời gian photon, trong khi $ \ Delta_t {emi} $ là khoảng thời gian mà chúng được phát ra.

$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$

$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$

$ \ Delta t_ {obs} $ sẽ mất nhiều thời gian hơn $ \ Delta t_ {emi} $ vì bộ dò sẽ nhận tất cả các photon.

$$ L_ {obs} = L_ {emi} \ left (\ frac {a_0} {a_e} \ right) ^ 2 $$

$$ L_ {obs} <L_ {emi} $$

$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$

Đối với một vũ trụ không giãn nở, khoảng cách độ sáng giống như khoảng cách đi tới.

$$ d_L = r_c $$

$$ \ Rightarrow f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$

$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left (\ frac {a_e} {a_0} \ right) ^ 2 $$

$$ \ Rightarrow d_L = r_c \ left (\ frac {a_0} {a_e} \ right) $$

Chúng tôi đang tìm khoảng cách độ sáng $ d_L $ để tính độ sáng của vật thể phát ra $ L_ {emi} $ -

• Interpretation - Nếu chúng ta biết sự chuyển dịch màu đỏ zcủa bất kỳ thiên hà nào, chúng ta có thể tìm ra $ d_A $ và từ đó chúng ta có thể tính được $ r_c $. Điều này được sử dụng để tìm ra $ d_L $.

• Nếu $ d_L! = r_c (a_0 / a_e) $, thì chúng ta không thể tìm thấy Lemi từ $ f_ {obs} $.

Mối quan hệ giữa Khoảng cách độ sáng $ d_L $ và Khoảng cách đường kính góc $ d_A. $

Chúng tôi biết rằng -

$$ d_A (z_ {gal}) = \ frac {d_L} {1 + z_ {gal}} \ left (\ frac {a_0} {a_e} \ right) $$

$$ d_L = (1 + z_ {gal}) d_A (z_ {gal}) \ left (\ frac {a_0} {a_e} \ right) $$

Hệ số tỷ lệ khi các photon được phát ra được cho bởi:

$$ a_e = \ frac {1} {(1 + z_ {gal})} $$

Hệ số tỷ lệ cho vũ trụ hiện tại là -

$$ a_0 = 1 $$

$$ d_L = (1 + z_ {gal}) ^ 2d_ \ wedge (z_ {gal}) $$

Cái nào để chọn $ d_L $ hoặc $ d_A $?

• Đối với một thiên hà có kích thước đã biết và độ dịch chuyển màu đỏ để tính toán độ lớn của nó, thì $ d_A $ được sử dụng.

• Nếu có một thiên hà có độ lớn biểu kiến ​​cho trước, thì để xác định độ lớn của nó, $ d_L $ được sử dụng.

Example - Nếu cho rằng hai thiên hà có độ dịch chuyển đỏ bằng nhau (z = 1) và trong mặt phẳng bầu trời, chúng cách nhau 2.3 arc sec thì khoảng cách vật lý tối đa giữa hai chất đó là bao nhiêu?

Đối với điều này, hãy sử dụng $ d_A $ như sau:

$$ d_A (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $$

trong đó z = 1 thay thế cho H (z) dựa trên các tham số vũ trụ học của các thiên hà.

Những điểm cần nhớ

• Khoảng cách độ sáng phụ thuộc vào cosmology.

• Nếu biết độ sáng nội tại $ d_L $ của một vật thể ở xa, chúng ta có thể tính độ sáng của nó bằng cách đo thông lượng f.

• Đối với một vũ trụ không giãn nở, khoảng cách độ sáng giống như comoving distance.

• Khoảng cách độ sáng luôn lớn hơn Angular Diameter Distance.

Đối với bất kỳ dịch chuyển đỏ (z) nào đã cho, chúng ta có hai giá trị cho khoảng cách -

• Khoảng cách đường kính góc (d _A )
• Khoảng cách độ sáng (d _L )

Không có định nghĩa duy nhất về khoảng cách "vũ trụ" trong vũ trụ. Việc lựa chọn khoảng cách tùy thuộc vào mục đích và sự thuận tiện khi áp dụng.

Để kiểm tra xu hướng dự đoán về kích thước góc của một vật thể thay đổi như thế nào theo dịch chuyển đỏ, cần có thước đo kích thước tiêu chuẩn trên bầu trời. Đây phải là một đối tượng -

• rất sáng, vì vậy nó có thể được phát hiện ở z> 1.

• rất lớn, để chúng ta có thể phân giải kích thước góc của nó.

• không phát triển về mặt hình thái theo thời gian quan trọng về mặt vũ trụ (z ∼ 1 tương ứng với thời gian nhìn lại khoảng 7 Gyr).

Một số vật thể (như thiên hà cD) thỏa mãn hai tiêu chí đầu tiên. Nhưng hầu hết mọi vật thể đều phát triển về mặt hình thái theo thời gian. Nói chung, các vật thể vật lý thiên văn (nguồn mở rộng) có xu hướng nhỏ hơn về bản chất trong quá khứ vì chúng vẫn đang hình thành.

Khoảng cách độ sáng

Khoảng cách độ sáng phụ thuộc vào vũ trụ học. Sự phụ thuộc của khoảng cách độ sáng vào vũ trụ học làm cho nó trở thành một thước đo hữu ích cho các tham số vũ trụ học.

Các thông số vũ trụ có thể được ước tính nếu chúng ta có thể tìm thấy một ngọn nến tiêu chuẩn không tiến hóa về bản chất và tồn tại từ vũ trụ cục bộ đến dịch chuyển đỏ cao.

Nến tiêu chuẩn là nến không khác nhau về độ sáng của nó từ nguồn này sang nguồn khác. Tiền đề là bất kỳ sự khác biệt nào về độ sáng ước tính của nến tiêu chuẩn đều phải do vũ trụ học. Một trong những ngọn nến như vậy là Siêu tân tinh Loại Ia.

Siêu tân tinh loại 1a (SNe)

Đây là kết quả của vụ nổ sao lùn trắng sau khi được bồi tụ đủ khối lượng từ người bạn đồng hành của nó, sao khổng lồ đỏ hoặc sao dãy chính tương tự, trong một hệ nhị phân. Sau khi sao khổng lồ đỏ đến gần hơn khoảng cách thùy Roche của sao lùn Trắng, quá trình chuyển khối bắt đầu và cuối cùng sao lùn trắng phát nổ tạo ra một lượng năng lượng khổng lồ, không để lại lõi nào. Chúng được gọi là Siêu tân tinh Loại 1a. Tốc độ điển hình của vụ nổ Siêu tân tinh Loại 1a trong một thiên hà là 1 mỗi thế kỷ.

Việc tìm kiếm SNe Loại 1a đã và đang diễn ra với các nhóm khác nhau -

• Nhóm Tìm kiếm Siêu tân tinh High z (Brian Schmidt, Adam Reiss và cộng sự)
• Dự án vũ trụ siêu tân tinh (Saul Perlmutter et al.)

Đã có một nhóm nghiên cứu khác được gọi là Carnegie Supernovae Project người đã đưa ra kết quả tương tự.

Sự giống nhau của các kết quả từ các nhóm khác nhau cho thấy bản chất vũ trụ học của Loại 1a SNe. Do đó, chúng là nến tiêu chuẩn hiệu quả.

Những điểm cần nhớ

• Không có định nghĩa duy nhất về khoảng cách "vũ trụ" trong vũ trụ.

• Khoảng cách đường kính góc và Khoảng cách độ sáng được sử dụng nhiều nhất.

• Nến tiêu chuẩn là nến không khác nhau về độ sáng của nó từ nguồn này sang nguồn khác.

• SNe loại 1a đáp ứng các tiêu chí của một nến tiêu chuẩn.

CMB (Nền vi sóng vũ trụ) về cơ bản được cấu thành bởi các photon ở thời điểm vật chất và bức xạ ở trạng thái cân bằng. Đến những năm 1920, ý tưởng về một vũ trụ giãn nở đã được chấp nhận và có thể trả lời một số câu hỏi. Nhưng các câu hỏi về sự phong phú của các nguyên tố nặng hơn và sự phong phú vẫn chưa được giải đáp. Hơn nữa, vũ trụ đang giãn nở ngụ ý rằng mật độ vật chất nên giảm xuống 0.

Năm 1948, George Gammow và Ralph Alpher giải thích Nguồn gốc của các nguyên tố nặng hơn và sự phong phú bằng cách sử dụng "Big Bang". Họ cùng với Robert Herman đã dự đoán sự tồn tại của "Bức xạ Relict" hoặc bức xạ còn lại từ "Vụ nổ lớn". Nhiệt độ dự đoán cho bức xạ tàn dư này là từ 50-6 K. Năm 1965, Robert Dicke, Jim Peebles và David Wilkinson cùng với Nhóm nghiên cứu của Amo Perizias đã phát hiện ra CMB trong thực nghiệm.

Vũ trụ sơ khai rất nóng và năng lượng quá cao khiến vật chất không thể duy trì trạng thái trung tính. Do đó, vật chất ở dạng ion hóa -Plasma. Bức xạ (photon) và Vật chất (plasma) tương tác chủ yếu thông qua ba quá trình sau.

• Compton Scattering - (Quá trình tương tác chính) Tán xạ không đàn hồi giữa photon năng lượng cao và hạt mang điện năng lượng thấp.

• Thomson Scattering - Sự tán xạ đàn hồi của photon bởi một hạt mang điện tự do.

• Inverse Compton Scattering- Hạt mang năng lượng cao và photon năng lượng thấp. Những tương tác này cuối cùng dẫn đến vật chất và bức xạ ở trạng thái cân bằng Nhiệt.

Cân bằng nhiệt

Ở trạng thái cân bằng nhiệt, bức xạ tuân theo Planck Distribution of Energy,

$$ B_v (T) = \ frac {2hv ^ 3} {c (e ^ {hv / k_BT} -1)} $$

Trong thời gian này, do các tương tác thường xuyên cao, đường đi tự do trung bình của các photon là rất nhỏ. Vũ trụ mờ đục đối với bức xạ. Vũ trụ sơ khai bị bức xạ chi phối. Vũ trụ phát triển theo cách mà vật chất và bức xạ đạt đến trạng thái Cân bằng Nhiệt và mật độ năng lượng của chúng trở nên bằng nhau. Điều này có thể được nhìn thấy từ biểu đồ thể hiện sự tiến hóa của mật độ với hệ số tỷ lệ. Chúng ta hãy tìm hệ số tỉ lệ (thời gian) (a (t)) mà tại đó vật chất và bức xạ đạt trạng thái cân bằng.

$$ \ rho_m \ propto \ frac {1} {a ^ 3}, \: \ rho_r \ propto \ frac {1} {a ^ 4} $$

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = \ frac {\ Omega_ { m, 0}} {\ Omega_ {r, 0}} a (t) $$

Ở trạng thái cân bằng,

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = 1 $$

$$ \ Rightarrow \ frac {\ Omega_ {m, 0}} {\ Omega_ {r, 0}} a (t) = 1 \: \ Rightarrow a (t) = 2,96 \ times 10 ^ {- 4} $$

bằng cách sử dụng $ \ Omega_ {m, 0} = 0,27 $ và $ \ Omega_ {r, 0} = 8 \ times 10 ^ {- 5} $. Sự dịch chuyển màu đỏ tương ứng với hệ số tỷ lệ này được cho bởi:

$$ z = 1 / a (t) -1 \ khoảng 3375 $$

Mật độ năng lượng của bức xạ giảm xuống do sự giãn nở của vũ trụ. Do đó, vũ trụ bắt đầu nguội dần. Khi năng lượng của các photon bắt đầu giảm, các nguyên tử trung hòa bắt đầu hình thành. Do đó, vào khoảng dịch chuyển đỏ 1300, Hydrogen trung tính bắt đầu hình thành. Thời đại này có nhiệt độ gần 3000K.

Sự tương tác giữa vật chất và bức xạ trở nên không thường xuyên và do đó vũ trụ bắt đầu trở nên trong suốt đối với bức xạ. Khoảng thời gian này được gọi là“Surface of last scattering”vì đường đi tự do trung bình của các photon trở nên rất lớn do đó hầu như không có sự tán xạ nào xảy ra sau khoảng thời gian này. Nó còn được gọi là“Cosmic Photosphere”.

Những điểm cần nhớ

• CMB được cấu thành bởi các photon tại thời điểm vật chất và bức xạ ở trạng thái cân bằng.

• Vũ trụ sơ khai rất nóng và năng lượng quá cao khiến vật chất không thể giữ được trung tính, vì vậy nó tồn tại dưới dạng vật chất ion hóa-Plasma.

• Tán xạ Compton, Tán xạ Thomson, Tán xạ Compton ngược là 3 quá trình tương tác bức xạ vật chất khi đó.

• Vũ trụ phát triển đến mức vật chất và bức xạ đạt đến trạng thái cân bằng Nhiệt.

Trước tiên, chúng ta nên hiểu những gì đặc trưng cho decoupling. Chúng ta biết rằng năng lượng cao hơn nhiều đến mức vật chất chỉ tồn tại ở dạngIonized Particles. Do đó, tại các kỷ nguyên tách và tái tổ hợp, năng lượng đã giảm xuống để cho phép ion hóa hydro. Một tính toán gần đúng có thể được thực hiện để ước tính nhiệt độ tại thời điểm tách.

Điều này đã được thực hiện như sau:

Đầu tiên, chỉ xem xét sự ion hóa của hydro ở trạng thái cơ bản.

$$ hv \ khoảng k_BT $$

$$ \ do đó T \ khoảng \ frac {hv} {k_B} $$

Để ion hóa hydro ở trạng thái cơ bản, hν là 13,6 eV và kB là Boltzmann Constant8,61 × 10 ⁻⁵ eV / K cho thấy nhiệt độ là 1,5 × 105 kelvin.

Điều này về cơ bản cho chúng ta biết rằng nếu nhiệt độ dưới 1,5 × 10 ⁵ K, các nguyên tử trung hòa có thể bắt đầu hình thành.

Chúng ta biết rằng tỷ lệ photon trên baryon là khoảng 5 × 10 ¹⁰ . Do đó, ngay cả ở phần cuối của biểu đồ nơi số lượng photon giảm đi, vẫn sẽ có đủ photon để ion hóa các nguyên tử hydro. Hơn nữa, sự tái kết hợp của electron và proton không đảm bảo một nguyên tử hydro ở trạng thái cơ bản. Các trạng thái bị kích thích đòi hỏi ít năng lượng hơn để ion hóa. Do đó, một phân tích thống kê có kỷ luật nên được thực hiện theo từng trường hợp để có được giá trị chính xác. Tính toán đặt nhiệt độ vào khoảng 3000K.

Để giải thích, chúng tôi xem xét trường hợp hydro kích thích vào trạng thái kích thích đầu tiên. Biểu thức tổng quát cho tỉ số giữa số photon có năng lượng hơnΔE, Nγ (> ΔE) tổng số photon Nγ được đưa ra bởi -

$$ \ frac {N_ \ gamma (> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {- \ Delta E} {kT}} $$

Đối với trường hợp hydro kích thích đến trạng thái kích thích đầu tiên, ΔElà 10,2 eV. Bây giờ, nếu chúng ta coi số lượng ít nhất 1 photon có năng lượng lớn hơn 10,2 cho mỗi baryon (hãy nhớ rằng tỷ lệ là 5 × 10 ¹⁰ , chúng ta thu được nhiệt độ từ phương trình 3 là 4800 K (Đã chèn Nγ (> ΔE) = Np).

Đây là nhiệt độ để tạo ra một quần thể các nguyên tử hydro trung hòa ở trạng thái kích thích đầu tiên. Nhiệt độ ion hóa này thấp hơn đáng kể. Do đó, chúng tôi có được một ước tính tốt hơn 1,5 × 10 ⁵ K, gần với giá trị được chấp nhận là 3000 K.

Dịch chuyển đỏ - Mối quan hệ nhiệt độ

Để hiểu mối quan hệ giữa dịch chuyển đỏ và nhiệt độ, chúng tôi sử dụng hai phương pháp sau như được mô tả dưới đây.

Phương pháp 1

Từ Wien’s Law, Chúng ta biết rằng

$$ \ lambda_mT = hằng $$

Để liên hệ điều này với dịch chuyển đỏ, chúng tôi sử dụng -

$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$

Khi $ λ_oT_o = λ_eT (z) $, chúng ta nhận được -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Cài đặt T_o như giá trị hiện tại 3K, chúng ta có thể nhận được giá trị nhiệt độ cho một dịch chuyển đỏ nhất định.

Phương pháp 2

Về tần suất, chúng tôi biết -

$$ v_0 = \ frac {v_e} {1 + z} $$

$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$

Điều này cho chúng ta biết về năng lượng ròng của các photon trong một khoảng năng lượng và hνlà năng lượng của một photon. Do đó, chúng ta có thể thu được số lượng photon bằngBνdν/hν.

Nếu $ n_ {νo} $ hiện tại và $ n_ {νe} $ cho số tiền đã phát, chúng ta nhận được -

$$ \ frac {n_ {v_e}} {n_ {v_0}} = (1 + z) ^ 3 $$

Khi đơn giản hóa, chúng tôi nhận được,

$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z) ^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$

Điều này cho chúng tôi Wien’s Law một lần nữa và do đó có thể kết luận rằng -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Những điểm cần nhớ

• Vũ trụ sơ khai rất nóng, ∼ 3000K.
• Các phép đo hiện tại cho thấy nhiệt độ của vũ trụ là gần 3K.
• Thời gian càng lùi xa, nhiệt độ càng tăng theo tỷ lệ thuận.

Trong chương này, chúng ta sẽ thảo luận về tính dị hướng của Bức xạ CMB và COBE, tức là Trình khám phá nền vũ trụ.

Anisotropies chính trong CMB

Để hiểu các quan sát từ không gian và các dị hướng cơ bản trong Bức xạ Nền Vi sóng Vũ trụ, chúng ta hãy lập các phương trình sau và hiểu nó như hình dưới đây.

CMB Mật độ số Photon (n _γ , 0)

$$ n _ {\ gamma, 0} = \ frac {Tổng \: năng lượng \: mật độ} {Đặc tính \: năng lượng \: của \: Photons} $$

$$ n _ {\ gamma, 0} = \ frac {aT_0 ^ 4} {k_BT_0} $$

$ K_B $ ở đâu Boltzmann Constant và $ T_0 $ là present temperature of the universe.

Sử dụng nhiệt độ hiện tại $ (T_0) $ là 2,7 K, chúng ta nhận được mật độ số photon CMB hiện tại là 400 cm ⁻³ .

Mật độ số photon của sao vũ trụ nhỏ hơn nhiều (∼ = 10 ⁻³ cm ⁻³ ) so với quy mô lớn.

Tỷ lệ Baryon trên Photon (η)

Nếu sự đóng góp của các ngôi sao từ các thiên hà trộn lẫn với CMB là không đáng kể, thì tỷ lệ baryon trên proton là -

$$ \ eta = \ frac {n_ {b, 0}} {n _ {\ gamma, 0}} $$

Giá trị hiện tại là ∼5 × 10 ⁻¹⁰ . Vì cả mật độ photon và số baryon đều tỷ lệ vớia⁻³, sau đó η không phát triển theo thời gian.

Mật độ năng lượng

Trái ngược với mật độ số, mật độ năng lượng vật chất chiếm ưu thế hơn so với mật độ năng lượng photon hiện nay.

Mật độ năng lượng của vật chất baryonic = $ \ rho_ {b, 0} c ^ 2 = 0,04 \ rho_cc ^ 2 = 2 × 10 ^ {- 9} ergcm ^ {- 3} $. Trong khi, Mật độ năng lượng của bức xạ = $ aT_0 ^ 4 = 4 \ times 10 ^ {- 13} ergcm {−3} $.

Tính đẳng hướng của bức xạ CMB

Penzias và Wilsonnhận thấy CMB là đẳng hướng trong giới hạn quan sát. Các giới hạn là độ phân giải góc và độ nhạy của dụng cụ thấp. Họ thực hiện các quan sát từ trái đất, do đó, các quan sát không thể được thực hiện qua tất cả các quang phổ vì hơi nước trong khí quyển hấp thụ nhiều bước sóng khác nhau, từ 1mm đến 1m. Vì vậy, CMB không thể được khẳng định là một phổ.

CMB được cho là bất biến quay (đẳng hướng). Vì đã tồn tại một thời điểm khi vật chất và bức xạ ở trạng thái cân bằng, nên việc hình thành các cấu trúc trong vũ trụ là không thể giải thích được. Vì sự phân bố của vật chất không phải là đẳng hướng mà được kết tụ lại với nhau như một mạng vũ trụ với những khoảng trống khổng lồ ở giữa, CMB được cho là có nguồn gốc ngoài thiên hà.

Nhưng, khi các quan sát từ không gian bắt đầu, các dị hướng trong CMB đã được tìm thấy, dẫn đến suy luận rằng các dị hướng này trong vật chất dẫn đến sự hình thành các cấu trúc.

Quan sát bức xạ CMB từ không gian

Các vệ tinh chính được phóng lên để quan sát CMB là -

• Cosmic Microwave Background Explorer (COBE, 1989)

• Wilkinson Microwave Anisotropy Probe (WMAP, 2001) và

• Planck (2009).

COBE (Trình khám phá nền vũ trụ)

COBE chủ yếu có hai công cụ. Họ đãFar InfraRed Absolute Spectrometer (FIRAS) và Differential Microwave Radiometers(Anten DMR). FIRAS đo cường độ của CMB dưới dạng hàm của bước sóng dọc theo bất kỳ hướng cụ thể nào. Trong khi đó, DMR có 3 ăng-ten để đo sự khác biệt về cường độ của CMB từ ba hướng khác nhau. Những gợi ý sau đây cung cấp cho chúng tôi thêm một số thông tin về FIRAS và DMR.

• Các quan sát CMB từ FIRAS cho thấy bức xạ CMB tương ứng với phổ vật đen tại T = 2.72528 ± 0.00065 K.

• DMR đo ba tần số (31,5 GHz, 53 GHz, 90 GHz) theo mọi hướng trên bầu trời.

• "Biểu tượng người dơi màu đỏ" trong các quan sát DMR là tiếng ồn từ phát xạ tiền cảnh (phát xạ đồng bộ khuếch tán thiên hà).

• Sự thay đổi cường độ trong các quan sát tương ứng với sự thay đổi nhiệt độ. Sự hiện diện của các điểm nóng và điểm lạnh chứng tỏ bức xạ CMB có tính dị hướng.

• Tính dị hướng này phải có tại thời điểm tách vì không có biến dạng trong CMB. Vì vậy, vật chất nên có một số túi với mật độ cao hơn các túi khác.

Kết quả COBE

Quang phổ CMB (cường độ như một hàm của năng lượng) gần như là một vật đen hoàn hảo ứng với T = 2,7 K. Cường độ riêng của bức xạ CMB gần như giống nhau đối với tất cả các phương. Xác nhận rằng vũ trụ là đẳng hướng ở quy mô lớn (xác nhận giả định của chúng ta về nguyên lý vũ trụ).

Phân tích dữ liệu cho thấy có sự dị hướng nhiệt độ (“dao động”) trong phổ CMB ở độ phân giải COBE (DMR).

Resolution of COBE, WMAP, Planck

• Thiết bị DMR trên bo mạch COBE có độ phân giải không gian giới hạn (tối đa) là ∼ 7 độ.

• Wilkinson Microwave Anisotropy Probe (WMAP) có độ phân giải trung bình là 0,7 độ.

• Vệ tinh Planck có độ phân giải góc ∼ 10 cung-phút.

Những điểm cần nhớ

• Mật độ số photon sao vũ trụ nhỏ hơn nhiều so với mật độ số photon CMB.

• Chúng ta đang sống trong một vũ trụ chi phối vật chất, vì mật độ năng lượng vật chất cao hơn mật độ năng lượng photon.

• COBE, WMAP, Planck là những nỗ lực để đo lường và định lượng các chất dị hướng trong CMB.

• Sự hình thành cấu trúc trong vũ trụ là kết quả của dị hướng CMB.

Khi chúng tôi nhìn vào bản đồ CMB bầu trời đã được tinh chỉnh, chỉnh sửa, có rất nhiều ô nhiễm tiền cảnh, đó là một loại anisotropytrong các bản đồ này. Chúng ta có thể thấy rằng những khí thải tiền cảnh này là từ dải ngân hà. Cường độ của CMB cao dọc theo mặt phẳng của mặt phẳng thiên hà và giảm cường độ khi chúng ta di chuyển ra xa. Trong đó, chúng ta có thể quan sát các dị hướng thứ cấp, là sự phát xạ đồng bộ từ thiên hà. Các khí thải này tạo nên ô nhiễm nền trước. Để xem xét lượng phát xạ CMB từ bầu trời, chúng ta cần phải trừ đi các phát thải tiền cảnh này.

Hình ảnh sau đây cho thấy CMB với phát xạ tiền cảnh.

Dipole Anisotropy

Có một loại dị hướng khác, được tìm thấy trong bản đồ toàn bầu trời CMB, nó được gọi là Dị hướng lưỡng cực. Nó không liên quan đến vũ trụ sơ khai. Điều này có thể được biểu diễn bằng cách sử dụng các hàm điều hòa hình cầu. Nếu có một mẫu trên bề mặt hình cầu và chúng ta muốn ánh xạ nó bằng các hàm toán học, chúng ta có thể làm như vậy bằng cách sử dụng các hàm lượng giác. Vì vậy, khi chúng ta lập bản đồ, nó có thể là một đơn cực - giống nhau ở mọi hướng, hoặc một lưỡng cực - đảo lộn các đặc tính khi xoay 180 độ. Tương tự, chúng ta có tứ cực và như vậy. Đối với một mẫu phức tạp, nó có thể được biểu thị bằng tổng của các đơn cực, lưỡng cực, tứ cực, v.v.

CMB được mô hình hóa theo cách mà một trong những nguồn chính gây dị hướng trong toàn bộ bản đồ bầu trời là dị hướng lưỡng cực này, nhưng nó không phải là mô hình ban đầu của CMB. Điều này có thể được nhìn thấy trong hình ảnh dưới đây.

Hướng lưỡng cực mà chúng ta thấy không phải là hướng ngẫu nhiên. Dị hướng lưỡng cực có hướng. Ta thấy cường độ CMB dọc theo một hướng xác định. Hướng này là do vector vận tốc của hệ mặt trời. Vận tốc của trái đất có thể được biểu thị theo mặt trời hoặc trung tâm của thiên hà. Hướng mà trái đất đang chuyển động, chúng ta quan sát thấy một Blueshift và Redshift và lưỡng cực nằm dọc theo hướng này.

Hình ảnh trên có dạng lưỡng cực điển hình vì Thiên hà của chúng ta đang di chuyển theo một hướng cụ thể. Kết quả là - một bên của bầu trời sẽ xuất hiện Dịch chuyển đỏ và bên kia bầu trời sẽ xuất hiện Dịch chuyển. Trong trường hợp này, Dịch chuyển đỏ có nghĩa là các photon có bước sóng dài hơn = lạnh hơn (vì vậy ngược lại so với tên của chúng, chúng trông có màu xanh lam trong biểu đồ trên).

Có thể nói, trái đất đang chuyển động theo một hướng cụ thể nào đó so với mặt trời / tâm thiên hà / CMB trên bầu trời tại một thời điểm nhất định. Sau đó, nếu chúng ta nhìn vào một góc bất kỳ và đo nhiệt độ cho CMB, nó sẽ khác. Điều này là do, chúng tôi đang đo các photon được Dịch chuyển màu xanh hoặc Dịch chuyển đỏ và phụ thuộc vào đường ngắm của các photon trên bầu trời.

Những điểm cần nhớ

• Sự ô nhiễm tiền cảnh trong CMB all sky map được gọi là dị hướng của CMB.

• Những khí thải này là từ dải ngân hà của chúng ta.

• 2 loại dị hướng là: Dị hướng lưỡng cực và dị hướng phổ công suất góc.

• Dị hướng lưỡng cực là theo một hướng cụ thể, trong khi dị hướng Phổ công suất góc được lan truyền khắp nơi.

Chiều dài đường chân trời là khoảng cách di chuyển của các photon ánh sáng từ 'Vụ nổ lớn' đến 'Kỷ nguyên tái hợp'. 1 ^st đỉnh của quang phổ góc là θ = 1◦ (l = 180), mà là một quy mô chiều dài rất đặc biệt.

Khoảng cách thích hợp giữa hai điểm được cho bởi -

$$ r_p = \ int_ {0} ^ {t} cdt $$

Khi chúng ta lấy khung thời gian từ t = 0 đến t = t _rec thì

$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$

Trong đó $ r_H $ là khoảng cách đường chân trời thích hợp.

Bây giờ, chúng tôi biết rằng -

$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ dt = \ frac {da} {\ dot {a}} $$

Khi t = 0 thì a = 0.

Khi đó $ t = t_ {rec}, a = a_0 / (1 + z_ {rec}) $.

Do đó, chúng ta có thể viết,

$$ r_H (z_ {rec}) = \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$

$$ H (a_ {rec}) = H (z_ {rec}) = H_0 \ sqrt {\ Omega_ {m, 0}} a ^ {- 3/2} $$

Trong Recombination period universevật chất bị chi phối. I E,Ωrad << Ωmatter. Do đó, thuật ngữ bức xạ bị loại bỏ.

$$ r_H (z_ {rec}) = \ frac {c} {H_0 \ sqrt {\ Omega_ {m, 0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$

$$ r_H (z_ {rec}) = \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m, 0}}} \ frac {1} {(1 + z_ {rec}) ^ {3/2}} $$

$$ \ theta_H (rec) = \ frac {r_H (z_ {rec})} {d_A (z_ {rec})} $$

Bằng 0,5 độ, nếu chúng ta đặt tất cả các giá trị đã biết vào phương trình.

Các Electromagnetic radiationlà mờ đục từ bề mặt của lần phân tán cuối cùng. Bất kỳ hai điểm nào 'không' nằm trong đường chân trời của nhau không cần phải có cùng tính chất. Vì vậy, nó sẽ cho các giá trị nhiệt độ khác nhau.

Chúng ta có thể có hai điểm trên bề mặt này không giao nhau, có nghĩa là tại một thời điểm vũ trụ giãn nở nhanh hơn tốc độ ánh sáng, đó là mô hình lạm phát cho sự giãn nở.

Những điểm cần nhớ

• Chiều dài đường chân trời là khoảng cách di chuyển của các photon ánh sáng từ 'Vụ nổ lớn' đến 'Kỷ nguyên tái hợp'.

• Trong thời kỳ Tái tổ hợp, vũ trụ là vật chất thống trị.

• Bức xạ điện từ không rõ ràng so với bề mặt của lần tán xạ cuối cùng.

Astrobiologylà nghiên cứu về nguồn gốc, sự tiến hóa, sự phân bố và tương lai của sự sống trong vũ trụ. Nó liên quan đến việc khám phá và phát hiệnExtrasolar Planets.

Astrobiology giải quyết các điểm sau -

• Cuộc sống bắt đầu và phát triển như thế nào? (sinh học + địa chất + hóa học + khoa học khí quyển)

• Có những thế giới bên ngoài trái đất thuận lợi cho sự sống không? (thiên văn học)

• Tương lai của cuộc sống trên trái đất sẽ như thế nào?

Astronomy giải quyết các điểm sau -

• Làm thế nào để phát hiện hệ thống hành tinh xung quanh các ngôi sao khác?

• Một trong những phương pháp là chụp ảnh trực tiếp, nhưng đây là một nhiệm vụ rất khó khăn vì các hành tinh là nguồn ánh sáng cực kỳ mờ nhạt so với các ngôi sao, và ánh sáng ít ỏi từ chúng có xu hướng bị mất đi trong ánh sáng chói từ ngôi sao mẹ của chúng.

• Độ tương phản tốt hơn khi hành tinh ở gần ngôi sao mẹ hơn và nóng hơn, do đó nó phát ra bức xạ hồng ngoại cường độ cao. Chúng ta có thể tạo ảnh trong vùng hồng ngoại.

Kỹ thuật phát hiện hành tinh ngoài hệ mặt trời

Các kỹ thuật hiệu quả nhất để phát hiện hành tinh ngoài hệ mặt trời như sau. Mỗi điều này cũng được giải thích chi tiết trong các chương tiếp theo.

Phương pháp vận tốc xuyên tâm

Nó còn được gọi là phương pháp Doppler. Trong này -

• Hệ thống hành tinh sao xoay quanh trung tâm của chúng, các ngôi sao chao đảo.

• Có thể phát hiện sự lắc lư bằng

  • Thay đổi định kỳ Đỏ / Xanh lam. Astrometry - đo các vật thể trên bầu trời rất chính xác.

Phương thức chuyển tuyến

Phương pháp Transit (kính viễn vọng không gian Kepler) được sử dụng để tìm ra kích thước. Độ sáng của sao theo hành tinh thường rất ít, không giống như trong hệ nhị phân.

Hình ảnh trực tiếp

Chụp ảnh hành tinh bằng kính thiên văn.

Chúng ta hãy xem xét một nghiên cứu điển hình được thực hiện trên Phương pháp Vận tốc xuyên tâm.

Nghiên cứu điển hình

Nghiên cứu trường hợp này là về quỹ đạo tròn và mặt phẳng của quỹ đạo vuông góc với mặt phẳng của bầu trời. Thời gian thực hiện của cả hai xung quanh trung tâm sẽ như nhau. Nó sẽ bằng chênh lệch múi giờ giữa hai Redshift hoặc Blueshift.

Hãy xem xét hình ảnh sau đây.

Tại A và C - vận tốc toàn phần được đo. Tại C, vận tốc bằng không.

• Vrmax = V _* là vận tốc thực của ngôi sao.

• P là khoảng thời gian của ngôi sao cũng như hành tinh.

• θ là pha của quỹ đạo.

• Khối lượng sao - M _* , bán kính quỹ đạo a _* , khối lượng hành tinhm_p.

Từ phương trình khối lượng tâm,

$$ m_p a_p = M_ \ ast a_ \ ast $$

Từ phương trình vận tốc,

$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$

$$ \ Rightarrow a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$

Từ Kepler’s Law,

$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$

$$ \ Rightarrow a_p = \ left (\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right) ^ {1/3} $$

Từ các phương trình trên, chúng ta nhận được -

$$ \ Rightarrow m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$

Chúng tôi nhận được: $ m_p, a_p $ và $ a_ \ ast $.

Phương trình trên thiên về hầu hết các hành tinh có khối lượng lớn gần với ngôi sao.

Những điểm cần nhớ

• Astrobiology là nghiên cứu về nguồn gốc, sự tiến hóa, sự phân bố và tương lai của sự sống trong vũ trụ.

• Các kỹ thuật để phát hiện các hành tinh ngoài hệ mặt trời là: Phương pháp Vận tốc xuyên tâm, Phương pháp Chuyển tuyến, Hình ảnh Trực tiếp, v.v.

• Sự dao động có thể được phát hiện bằng sự thay đổi định kỳ màu đỏ / xanh lam và Phép đo thiên văn.

• Phương pháp Vận tốc xuyên tâm thiên về phát hiện các hành tinh lớn gần ngôi sao.

Trong chương trước, Phương pháp Vận tốc xuyên tâm cho trường hợp mặt phẳng quỹ đạo và mặt phẳng bầu trời vuông góc với nhau đã được thảo luận đối với quỹ đạo tròn. Ở đây, chúng ta giải quyết một trường hợp nữa, khi mặt phẳng quỹ đạo và mặt phẳng bầu trời không vuông góc với quỹ đạo tròn.

Khi mặt phẳng quỹ đạo nghiêng một góc so với mặt phẳng bầu trời (không vuông góc), chúng ta có tình huống sau:

Trong trường hợp này, khi chúng vuông góc, chúng ta có hai điểm tại đó chúng ta có thể đo vận tốc thực. Nhưng ở đây, điều đó là không thể. Tại tất cả các điểm, chúng tôi chỉ có thể đo một thành phần của vận tốc thực,v.

$$ v_r = v \: sin (i) cos (\ theta) $$

Ở đâu θlà pha của quỹ đạo là đại lượng phụ thuộc thời gian. Góc nghiêngimặt khác, không phụ thuộc vào thời gian. Vì thế,

$$ (v_r) _ {max} = v \: sin (i) $$

Đường cong vận tốc xuyên tâm quan sát được sẽ có dạng sau:

Khi mặt phẳng quỹ đạo vuông góc với bầu trời -

$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ $

Ở đâu m_p, P, G, M∗lần lượt là khối lượng của hành tinh, chu kỳ quỹ đạo, hằng số hấp dẫn vũ trụ và khối lượng của ngôi sao. Nhưng trong trường hợp này, chúng ta nên sửa đổi nó như sau:

$$ m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {max} $$

Nhưng, việc tìm ra giá trị của i là một việc khó. Chúng tôi có thể áp đặt những ràng buộc nhất định đối với giá trị củaisử dụng phương thức trung chuyển. Hành tinh đi qua giữa ngôi sao và Trái đất được gọi là quá cảnh. Chúng ta có thể thu được đường cong ánh sáng bằng cách quan sát sự chuyển tiếp và sự sụt giảm đáng kể trong thông lượng quan sát được của đường cong ánh sáng ngụ ý rằng i gần 90 độ. Nếu các điều kiện đó không được thỏa mãn, chúng tôi không thể có bất kỳ ý tưởng nào về giá trị củai. Sau đó, giá trị củam_p mà chúng tôi nhận thấy có thể đóng vai trò là giới hạn thấp hơn cho khối lượng của hành tinh, vì nó thực sự là m_p sin(i) và sin(i) ≤ 1.

Để kết luận, phương pháp vận tốc xuyên tâm thuận tiện hơn phương pháp vận chuyển vì vận tốc xuyên tâm có thể được đo bất kỳ lúc nào nhưng các phép đo vận tốc chỉ có thể được thực hiện trong quá trình vận chuyển có thể không kéo dài lâu.

Những điểm cần nhớ

• Việc tìm độ nghiêng của quỹ đạo hành tinh không đạt được bằng phương pháp Vận tốc xuyên tâm.

• Phương pháp Vận tốc xuyên tâm tốt hơn Phương pháp Chuyển tuyến vì vận tốc xuyên tâm có thể được đo luôn không giống như vận chuyển.

• Quá trình chuyển tuyến diễn ra trong thời gian ngắn và rất dễ bị bỏ lỡ.

Phương thức vận chuyển (Kepler Space Telescope)được sử dụng để tìm ra kích thước. Độ sáng của một ngôi sao bởi một hành tinh thường rất ít không giống như một hệ nhị phân.

• F₀ là dòng chảy của ngôi sao trước khi hành tinh xảy ra nó.

• F₁ là thông lượng sau khi toàn bộ hành tinh ở phía trước ngôi sao.

Hình ảnh sau đây sẽ được sử dụng cho tất cả các phép tính.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$

$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0,001 \% $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$

Điều này không dễ đạt được bằng kính thiên văn trên mặt đất. Nó đạt được nhờ kính thiên văn Hubble.

Ở đây, $ t_T $ là thời gian giữa vị trí A và D và $ t_F $ là thời gian giữa vị trí B và C.

Hình dạng của phương tiện liên quan đến độ nghiêng icủa hệ thống. Vĩ độ và độ nghiêng chuyển tuyến có thể hoán đổi cho nhau.

Từ những hình ảnh trên, chúng ta có thể viết -

$$ \ frac {h} {a} = cos (i) $$

$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$

$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$

$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$

$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$

$$ sin (\ theta) = \ frac {y} {a} $$

$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$

$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$

Ở đây, $ t_T $ là phần của khoảng thời gian mà quá trình chuyển tuyến xảy ra và (2θ / 2π) là phần nhỏ của góc mà quá trình chuyển tuyến xảy ra.

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Thông thường, a >> R ∗ >> Rp. Vì vậy, chúng ta có thể viết -

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Đây, Plà khoảng thời gian giữa hai lần chuyển tiếp liên tiếp. Thời gian vận chuyển rất ít hơn so với khoảng thời gian quỹ đạo. Vì thế,

$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$

Đây, t_T, P, R∗ là những người có thể quan sát, a và i nên được tìm ra.

Hiện nay,

$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

trong đó, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.

Để cho,

$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$

Bây giờ, chúng ta có thể bày tỏ,

$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$

Đối với các ngôi sao của chuỗi chính,

$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$

$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$

Điều này cho R∗.

Do đó, chúng tôi cũng nhận được giá trị của 'a'.

Vì vậy, chúng ta nhận được 'R _p ', 'ap' và thậm chí là 'i'.

Cho tất cả điều này,

$$ h \ leq R_ \ ast + R_p $$

$$ a \: cos \: i \ leq R_ \ ast + R_p $$

Đối với thậm chí ~ 89 độ, thời gian vận chuyển là rất nhỏ. Hành tinh phải ở rất gần để có đủ thời gian vận chuyển. Điều này tạo ra một hạn chế chặt chẽ đối với 'i'. Khi chúng ta nhận được 'i', chúng ta có thể suy ra 'm _p ′ từ phép đo vận tốc xuyên tâm.

Việc phát hiện bằng phương pháp chuyển tuyến này được gọi là phát hiện cơ hội, tức là xác suất quan sát thấy quá cảnh. Các phép tính xác suất quá cảnh (xác suất quan sát) được hiển thị bên dưới.

Xác suất chuyển tuyến liên quan đến góc vững chắc được xác định bởi hai cấu hình chuyển tuyến cực đoan, đó là -

$$ Solid \: angle \: of \: hành tinh \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$

Cũng như tổng góc đặc tại bán trục chính a, hoặc -

$$ Solid \: angle \: of \: bridge \: = \: 4 \ pi $$

Xác suất là tỷ lệ của hai khu vực này -

$$ = \: \ frac {area \: of \: sky \: che \: bởi \: thuận lợi \: hướng} {area \: of \: sky \: che \: bởi \: all \: có thể \: định hướng \: của \: quỹ đạo} $$

$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: blank \: cyclinder} {area \ : trong số \: hình cầu} $

Xác suất này không phụ thuộc vào người quan sát.

Những điểm cần nhớ

• Phương pháp Chuyển tuyến (Kính viễn vọng Không gian Kepler) được sử dụng để tìm ra kích thước.
• Phát hiện bằng Phương pháp chuyển tuyến là một phát hiện tình cờ.
• Hành tinh phải ở rất gần để có đủ thời gian vận chuyển.
• Xác suất chuyển tuyến liên quan đến góc rắn của hành tinh.
• Xác suất này không phụ thuộc vào hệ quy chiếu của người quan sát.

Hình ảnh trực tiếp đầu tiên về một hành tinh ngoài hệ mặt trời, vào năm 2004, là một hành tinh có khối lượng 3-10 M_jupiter quay quanh một ngôi sao lùn nâu (2M1207) với khối lượng 25 M_jupiter. Các kỹ thuật như Vận tốc xuyên tâm, Chuyển tiếp, Vilensing hấp dẫn, Hình ảnh, Đo lường thiên văn, v.v., đã được sử dụng để phát hiện các hành tinh ngoài hành tinh. Số lượng phát hiện đã tăng lên hàng năm.

Cho đến khoảng năm 2010, phương pháp vận tốc xuyên tâm đã được sử dụng rộng rãi, nhưng hiện nay hầu hết các phát hiện được thực hiện bằng phương pháp Transit. Số lượng phát hiện tăng đột biến trong năm 2014, đó là khiKepler Space Telescope (KST) bắt đầu đưa ra kết quả.

Phân bố theo chu kỳ khối lượng cho thấy rằng phương pháp Vận tốc xuyên tâm thiên về phát hiện các hành tinh lớn có chu kỳ lớn hơn, trong khi sử dụng phương pháp Chuyển tuyến, các hành tinh có chu kỳ thấp hơn chỉ được phát hiện như thể hiện trong hình ảnh sau (Được phép: NASA Exoplanet Archive) .

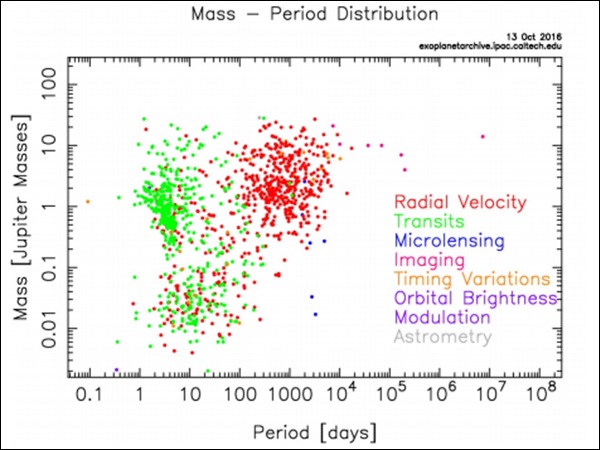
Số lượng phát hiện các hành tinh có khối lượng nhỏ hơn đã tăng lên đáng kể kể từ khi KST ra đời. Điều này được thể hiện rõ trong hình bên dưới. Các hành tinh được KST phát hiện được chia thành hai nhóm: các hành tinh có khối lượng lớn nóng được gọi là "Hot Jupiters" và các hành tinh có khối lượng thấp hơn được gọi là "Siêu Trái đất nóng" (vì chúng có khối lượng lớn hơn Trái đất).

Khi chúng tôi vẽ biểu đồ số lượng các hành tinh ngoài hệ mặt trời được phát hiện so với khoảng cách đến chúng, chúng tôi thấy rằng hầu hết các hành tinh này đều nằm trong phạm vi 2kpc, tức là nằm trong thiên hà của chúng ta. Có thể các hành tinh không quá hiếm trong vũ trụ, vì khả năng phát hiện của chúng ta chỉ giới hạn ở một số loại hành tinh nhất định trong một phần rất nhỏ của vũ trụ.

Các hành tinh được hình thành từ circumstellar disc hoặc là proto planetary disc. Nếu các hành tinh được hình thành như một sản phẩm phụ trong quá trình hình thành sao, có thể số lượng hành tinh trong vũ trụ vượt quá số lượng sao trong vũ trụ !!

Các khu vực sinh sống

Vùng có thể sống được có thể được định nghĩa là vùng xung quanh ngôi sao nơi nước có thể tồn tại ở dạng lỏng. Hãy xem xét một hành tinh ở khoảng cách $ a_p $ từ ngôi sao như thể hiện trong hình sau. Một phương pháp đơn giản để tính toán nhiệt độ của hành tinh được mô tả như sau.

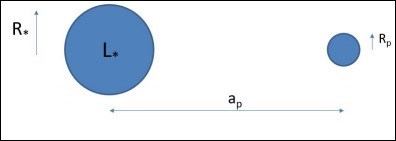
$$ \ left (\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right) \ pi R ^ 2_p (1 - A) = 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$

và

$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$

$$ \ do đó T_p = (1 - A) T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$

Trong trường hợp của chúng tôi thay thế

• L_sun = 3.83 x 10²⁶

• a_p = 1.5 ∗ 10¹¹ and

• A = 0.3

Sẽ cho $ T_ {Earth} = 255K $. Tính toán thực tế liên quan rất nhiều đến vật lý đám mây. Vùng có thể sống trong hệ mặt trời của chúng ta nằm giữa 0,9 AU và 1,7 AU.

Độ sáng của Mặt trời tăng dần theo thời gian do áp suất khí giảm. Nó kém sáng hơn 30% khi nó bắt đầu đốt cháy hydro. Điều này sẽ dẫn đến sự thay đổi của khu vực có thể sinh sống khỏi Mặt trời. Vì Trái đất ở gần rìa bên trong của Vùng có thể sống được, có thể một ngày nào đó nó sẽ di chuyển ra khỏi vùng!

Khu vực sinh sống liên tục

Trong ngắn hạn nó được gọi là CHZcó thể được định nghĩa là vùng mà nước lỏng có thể tồn tại trong toàn bộ thời gian tồn tại của Chuỗi chính của một ngôi sao. KST đã phát hiện ra nhiều hành tinh ngoài hệ mặt trời nằm trong vùng có thể sinh sống được.

Chữ ký sinh học là bất kỳ chất nào - chẳng hạn như một nguyên tố, đồng vị, phân tử hoặc hiện tượng cung cấp bằng chứng khoa học về sự sống trong quá khứ hoặc hiện tại. Một ví dụ là việc phát hiện cả O ₂ và CO ₂ trên một hành tinh, điều này thường không thể thực hiện được chỉ thông qua các quá trình địa chất. Việc phát hiện này được thực hiện bằng cách phân tích quang phổ hấp thụ.

Những điểm cần nhớ

• Các kỹ thuật như Vận tốc xuyên tâm, Chuyển tuyến, Vilensing hấp dẫn, Hình ảnh, Phép đo chiêm tinh, v.v., đã được sử dụng để phát hiện các hành tinh ngoài hành tinh.

• Phương pháp vận tốc xuyên tâm thiên về phát hiện các hành tinh lớn với chu kỳ lớn hơn.

• Các hành tinh có khối lượng lớn nóng được gọi là “Sao Mộc nóng” và các hành tinh có khối lượng thấp hơn được gọi là “Siêu Trái đất nóng”.

• Số lượng hành tinh trong vũ trụ vượt quá số lượng ngôi sao trong vũ trụ.

• Vùng có thể sống được có thể được định nghĩa là vùng xung quanh ngôi sao nơi nước có thể tồn tại ở dạng lỏng.