Mạch kỹ thuật số - Logic ngưỡng
Trong các chương trước, chúng ta đã thực hiện các mạch tổ hợp khác nhau bằng cách sử dụng các cổng logic. Ngoại trừ cổng NOT, tất cả các cổng logic còn lại có ít nhất hai đầu vào và đầu ra duy nhất. Tương tự,threshold gate cũng chứa ít nhất một đầu vào và chỉ một đầu ra.
Ngoài ra, nó chứa các trọng số tương ứng cho mỗi đầu vào và một giá trị ngưỡng. Giá trị của các trọng số và ngưỡng này có thể là một số thực hữu hạn bất kỳ.
Khái niệm cơ bản về cổng ngưỡng
Cho các đầu vào của cổng ngưỡng là X 1 , X 2 , X 3 ,…, X n . Trọng số tương ứng của các đầu vào này là W 1 , W 2 , W 3 ,…, W n . Cácsymbol của cổng Threshold được hiển thị trong hình sau.
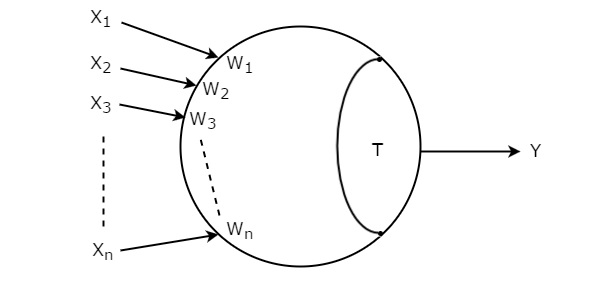
Threshold gateđược biểu diễn bằng một vòng tròn và nó có đầu vào 'n', X 1 đến X n và đầu ra duy nhất, Y. Vòng tròn này được làm thành hai phần. Một phần đại diện cho trọng số tương ứng với các đầu vào và phần khác đại diện cho giá trị Ngưỡng, T.
Tổng các sản phẩm của đầu vào có trọng số tương ứng được gọi là weighted sum. Nếu tổng trọng số này lớn hơn hoặc bằng giá trị Ngưỡng, T thì chỉ đầu ra, Y sẽ bằng một. Nếu không, đầu ra, Y sẽ bằng không.
Mathematically, chúng ta có thể viết mối quan hệ này giữa đầu vào và đầu ra của cổng Threshold như bên dưới.
$$ Y = 1, nếu \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0, ngược lại.
Do đó, chúng ta có thể triển khai các cổng logic khác nhau và các hàm Boolean chỉ bằng cách thay đổi các giá trị của trọng số và / hoặc giá trị Ngưỡng, T.
Thí dụ
Hãy để chúng tôi tìm simplified Boolean function cho cổng Threshold sau.

Cổng Threshold này có ba đầu vào X 1 , X 2 , X 3 và một đầu ra Y.
Trọng số tương ứng với các đầu vào X 1 , X 2 & X 3 lần lượt là W 1 = 2, W 2 = 1 & W 3 = -4.
Giá trị của cổng Threshold là T = -1.
Các weighted sum của cổng Threshold là
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Thay các trọng số đã cho vào phương trình trên.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
Đầu ra của cổng Threshold, Y sẽ là '1' nếu W ≥ −1, ngược lại sẽ là '0'.
Sau table cho thấy mối quan hệ giữa đầu vào và đầu ra cho tất cả các kết hợp đầu vào có thể có.
| Đầu vào | Tổng trọng lượng | Đầu ra | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Từ bảng trên, chúng ta có thể viết Boolean function cho đầu ra, Y là
$$ Y = \ sum m \ left (0,2,4,6,7 \ right) $$
Việc đơn giản hóa hàm Boolean này bằng cách sử dụng 3 variable K-Map được hiển thị trong hình sau.

Do đó, simplified Boolean function đối với cổng Ngưỡng cụ thể là $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Tổng hợp các chức năng ngưỡng
Cổng ngưỡng còn được gọi là universal gatebởi vì chúng ta có thể triển khai bất kỳ hàm Boolean nào bằng cách sử dụng (các) cổng Threshold. Đôi khi, có thể không thực hiện được một số cổng logic và các hàm Boolean bằng cách sử dụng cổng Threshold duy nhất. Trong trường hợp đó, chúng tôi có thể yêu cầu nhiều cổng Ngưỡng.
Làm theo những steps để triển khai một hàm Boolean bằng cách sử dụng cổng Threshold duy nhất.
Step 1 - Lập công thức Truth table cho hàm Boolean đã cho.
Step 2 - Trong bảng Sự thật ở trên, hãy thêm (bao gồm) một cột nữa, cho biết mối quan hệ giữa weighted sums và Threshold value.
Step 3 - Viết mối quan hệ giữa tổng trọng số và ngưỡng cho mỗi tổ hợp đầu vào như đề cập bên dưới.
Nếu đầu ra của hàm Boolean là 1, thì tổng có trọng số sẽ lớn hơn hoặc bằng giá trị Ngưỡng cho các kết hợp đầu vào đó.
Nếu đầu ra của hàm Boolean là 0, thì tổng có trọng số sẽ nhỏ hơn giá trị Ngưỡng cho các kết hợp đầu vào đó.
Step 4 - Chọn các giá trị của trọng số & Ngưỡng sao cho chúng phải thỏa mãn tất cả các quan hệ có trong cột cuối cùng của bảng trên.
step 5 - Vẽ symbol của cổng Threshold với các trọng số đó và giá trị Ngưỡng.
Thí dụ
Hãy để chúng tôi thực hiện những điều sau Boolean function sử dụng cổng Threshold duy nhất.
$$ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $$
Hàm Boolean đã cho là một hàm ba biến, được biểu diễn dưới dạng tổng của số hạng min. CácTruth table của chức năng này được hiển thị bên dưới.
| Đầu vào | Đầu ra | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Bây giờ, chúng ta hãy thêm (bao gồm) một cột nữa vào bảng Sự thật ở trên. Cột cuối cùng này chứa các mối quan hệ giữaweighted sums (W) and Threshold giá trị (T) cho mỗi sự kết hợp của các yếu tố đầu vào.
| Đầu vào | Đầu ra | Mối quan hệ giữa W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
Sau đây là kết luận từ bảng trên.
Giá trị của Threshold phải bằng 0 hoặc âm dựa trên quan hệ đầu tiên.
Giá trị của W 3 phải là số âm dựa trên quan hệ thứ nhất và thứ hai.
Giá trị của W 1 và W 2 phải lớn hơn hoặc bằng giá trị Ngưỡng dựa trên quan hệ thứ năm và thứ ba.
W 2 phải lớn hơn W 3 dựa trên quan hệ thứ tư.
Chúng ta có thể chọn các giá trị sau cho trọng số và Ngưỡng dựa trên các kết luận trên.
W 1 = 2, W 2 = 1, W 3 = -4 & T = -1
Các symbol của cổng Threshold với các giá trị trên được hiển thị bên dưới.

Do đó, cổng Threshold này thực hiện Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $.