Mạch kỹ thuật số - Nhận thức logic hai cấp độ
Số mức tối đa có giữa đầu vào và đầu ra là hai trong two level logic. Điều đó có nghĩa là, bất kể tổng số cổng logic, số lượng cổng Logic tối đa hiện có (xếp tầng) giữa bất kỳ đầu vào và đầu ra nào là hai trong hai mức logic. Ở đây, các đầu ra của cổng Logic cấp một được kết nối như là đầu vào của (các) cổng Logic cấp hai.
Hãy xem xét bốn cổng Logic AND, OR, NAND & NOR. Vì có 4 cổng Logic, chúng ta sẽ có 16 cách khả thi để nhận ra logic hai cấp. Đó là AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-HOẶC, NOR-NAND, NOR-NOR.
Các nhận thức logic hai cấp độ này có thể được phân thành hai loại sau.
- Dạng thoái hóa
- Dạng không thoái hóa
Dạng thoái hóa
Nếu đầu ra của nhận thức logic hai mức có thể đạt được bằng cách sử dụng cổng Logic đơn, thì nó được gọi là degenerative form. Rõ ràng, số lượng đầu vào của cổng Logic đơn lẻ tăng lên. Do đó, lượng người hâm mộ của cổng Logic tăng lên. Đây là một ưu điểm của dạng thoái hóa.
Chỉ có 6 combinationsthực hiện logic hai cấp trong số 16 tổ hợp có dạng suy biến. Đó là AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
Trong phần này, chúng ta hãy thảo luận về một số nhận thức. Giả sử, A, B, C & D là các đầu vào và Y là đầu ra trong mỗi hiện thực logic.
AND-AND logic
Trong hiện thực logic này, cổng AND có ở cả hai cấp độ. Hình dưới đây cho thấy một ví dụ choAND-AND logic hiện thực hóa.

Chúng ta sẽ nhận được kết quả đầu ra của cổng logic mức đầu tiên là $ Y_ {1} = AB $ và $ Y_ {2} = CD $
Các đầu ra này, $ Y_ {1} $ và $ Y_ {2} $ được áp dụng làm đầu vào của cổng AND hiện diện ở mức thứ hai. Vì vậy, đầu ra của cổng AND này là
$$ Y = Y_ {1} Y_ {2} $$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên.
$$ Y = \ left (AB \ right) \ left (CD \ right) $$
$ \ Rightarrow Y = ABCD $
Do đó, đầu ra của việc thực hiện logic AND-AND này là ABCD. Hàm Boolean này có thể được thực hiện bằng cách sử dụng cổng AND 4 đầu vào. Do đó, nó làdegenerative form.
Logic AND-NAND
Trong nhận thức logic này, các cổng AND có mặt ở mức đầu tiên và (các) cổng NAND có mặt ở mức thứ hai. Hình sau cho thấy một ví dụ choAND-NAND logic hiện thực hóa.
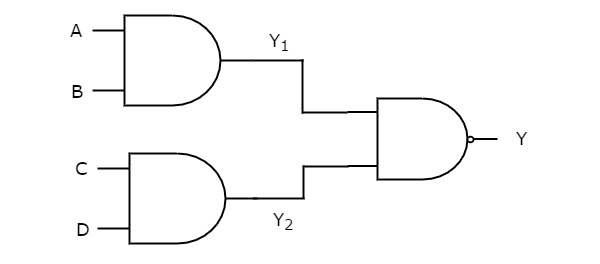
Trước đây, chúng tôi nhận được kết quả đầu ra của cổng logic cấp một là $ Y_ {1} = AB $ và $ Y_ {2} = CD $
Các đầu ra này, $ Y_ {1} $ và $ Y_ {2} $ được áp dụng làm đầu vào của cổng NAND có mặt ở cấp thứ hai. Vì vậy, đầu ra của cổng NAND này là
$$ Y = {\ left (Y_ {1} Y_ {2} \ right)} '$$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên.
$$ Y = {\ left (\ left (AB \ right) \ left (CD \ right) \ right)} '$$
$ \ Rightarrow Y = {\ left (ABCD \ right)} '$
Do đó, đầu ra của thực hiện logic AND-NAND này là $ {\ left (ABCD \ right)} '$. Hàm Boolean này có thể được thực hiện bằng cách sử dụng một cổng NAND 4 đầu vào. Do đó, nó làdegenerative form.
OR-HOẶC Logic
Trong nhận thức logic này, cổng OR có ở cả hai mức. Hình sau cho thấy một ví dụ choOR-OR logic hiện thực hóa.
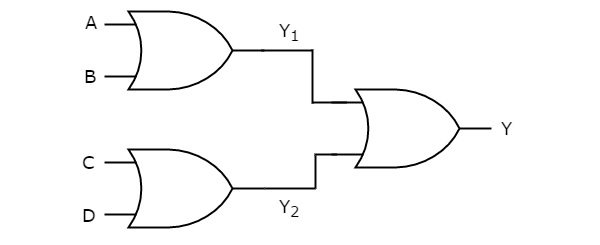
Chúng ta sẽ nhận được đầu ra của các cổng logic cấp một là $ Y_ {1} = A + B $ và $ Y_ {2} = C + D $.
Các đầu ra này, $ Y_ {1} $ và $ Y_ {2} $ được áp dụng làm đầu vào của cổng OR có ở cấp thứ hai. Vì vậy, đầu ra của cổng OR này là
$$ Y = Y_ {1} + Y_ {2} $$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên.
$$ Y = \ left (A + B \ right) + \ left (C + D \ right) $$
$ \ Rightarrow Y = A + B + C + D $
Do đó, đầu ra của hiện thực logic OR-OR này là A+B+C+D. Hàm Boolean này có thể được thực hiện bằng cách sử dụng cổng OR 4 đầu vào. Do đó, nó làdegenerative form.
Tương tự, bạn có thể xác minh xem các nhận thức còn lại có thuộc danh mục này hay không.
Dạng không thoái hóa
Nếu đầu ra của hiện thực logic hai mức không thể đạt được bằng cách sử dụng cổng logic đơn, thì nó được gọi là non-degenerative form.
Phần còn lại 10 combinationscủa hai cấp độ nhận thức logic dưới dạng không tạo ra. Đó là AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Bây giờ, chúng ta hãy thảo luận về một số nhận thức. Giả sử, A, B, C & D là các đầu vào và Y là đầu ra trong mỗi hiện thực logic.
VÀ-HOẶC logic
Trong nhận thức logic này, các cổng AND có mặt ở mức đầu tiên và (các) cổng OR có ở mức thứ hai. Hình dưới đây cho thấy một ví dụ choAND-OR logic hiện thực hóa.

Trước đây, chúng ta nhận được kết quả đầu ra của cổng logic cấp một là $ Y_ {1} = AB $ và $ Y_ {2} = CD $.
Các đầu ra này, Y1 và Y2 được áp dụng làm đầu vào của cổng OR có ở mức thứ hai. Vì vậy, đầu ra của cổng OR này là
$$ Y = Y_ {1} + Y_ {2} $$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên
$$ Y = AB + CD $$
Do đó, đầu ra của hiện thực logic AND-OR này là AB+CD. Hàm Boolean này nằm trongSum of Productshình thức. Vì chúng tôi không thể triển khai nó bằng cách sử dụng một cổng logic duy nhất, việc thực hiện logic AND-OR này lànon-degenerative form.
Logic AND-NOR
Trong nhận thức logic này, các cổng AND hiện diện ở mức đầu tiên và (các) cổng NOR có ở mức thứ hai. Hình sau cho thấy một ví dụ choAND-NOR logic hiện thực hóa.

Chúng ta biết đầu ra của cổng logic cấp một là $ Y_ {1} = AB $ và $ Y_ {2} = CD $
Các đầu ra này, Y1 và Y2 được áp dụng làm đầu vào của cổng NOR có ở mức thứ hai. Vì vậy, đầu ra của cổng NOR này là
$$ Y = {\ left (Y_ {1} + Y_ {2} \ right)} '$$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên.
$$ Y = {\ left (AB + CD \ right)} '$$
Do đó, đầu ra của hiện thực logic AND-NOR này là $ {\ left (AB + CD \ right)} '$. Hàm Boolean này nằm trongAND-OR-Inverthình thức. Vì chúng ta không thể triển khai nó bằng cách sử dụng một cổng logic duy nhất, việc thực hiện logic AND-NOR này lànon-degenerative form
HOẶC VÀ Logic
Trong nhận thức logic này, các cổng OR có ở mức đầu tiên và (các) cổng AND có ở mức thứ hai. Hình sau cho thấy một ví dụ choOR-AND logic hiện thực hóa.

Trước đây, chúng ta nhận được kết quả đầu ra của cổng logic cấp một là $ Y_ {1} = A + B $ và $ Y_ {2} = C + D $.
Các đầu ra này, $ Y_ {1} $ và $ Y_ {2} $ được áp dụng làm đầu vào của cổng AND hiện diện ở mức thứ hai. Vì vậy, đầu ra của cổng AND này là
$$ Y = Y_ {1} Y_ {2} $$
Thay các giá trị $ Y_ {1} $ và $ Y_ {2} $ trong phương trình trên.
$$ Y = \ left (A + B \ right) \ left (C + D \ right) $$
Do đó, đầu ra của hiện thực logic OR-AND này là (A + B) (C + D). Hàm Boolean này nằm trongProduct of Sumshình thức. Vì chúng tôi không thể triển khai nó bằng cách sử dụng cổng logic duy nhất, việc thực hiện logic OR-AND này lànon-degenerative form.
Tương tự, bạn có thể xác minh xem các nhận thức còn lại có thuộc danh mục này hay không.